Positioning
Vol.06 No.03(2015), Article ID:58262,11 pages
10.4236/pos.2015.63006
Towards a Semi-Kinematic Datum for Egypt
Mostafa Rabah1, Ahmed Shaker2, Magda Farhan3
1National Research Institute of Astronomy & Geophysics (NRIAG), Cairo, Egypt
2Faculty of Engineering-Shoubra, Benha University, Cairo, Egypt
3Faculty of Engineering, Kafr Elshiech University, Kafr Elshiech, Egypt
Email: mostafa_rabah@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 May 2015; accepted 20 July 2015; published 24 July 2015
ABSTRACT
Since 1990, positioning technology has undergone a dramatic improvement in terms of accuracy and accessibility. Prior to 1990, national geodetic datums were considered to be static with fixed coordinates assigned to the datum origin by convention. Datum coordinates were dynamic only as a consequence of re-observation and re-adjustment, or localized disturbance. This strategy has been suitable for terrestrial surveys within stable continental areas. The accessibility of Precise Point Positioning “PPP” is now widespread with the provision of free online processing facilities by various geodetic agencies. Such ready accessibility to a global datum has serious implication for this technology with static geocentric datums. The Geocentric Datum of Egypt (ITRF1994 Epoch 1996 based on GPS Observation Campaign 1996), for example, is now offset by −42.0 to +32.0cm from the ITRF2008 Epoch 2015 due to the inexorable tectonic movements of the Nubian plate since the datum realization in 1996. Unless the local geocentric datums are kept in step with global terrestrial reference frames, discrepancies between the two will increase in magnitude over time and will become discernable, even using PPP. The PPP users nowadays are unaware of this datum offset and incorrectly assume that a coordinated datum monument is in error if there is found to be a disagreement greater than the level of accuracy of the positioning technique. In this study, to avoid the discrepancies between the applied datum and On-Line GNSS Services, a semi-kinematic datum and related deformation mode are proposed for Egypt. The result also confirmed that the PMM model was giving good performance for the other parts out of Egypt. The evaluation study shows the best performances for the Egyptian deformation model over the ITRF2008 PMM.
Keywords:
Geodetic Datum, Precise Point Positioning, Plate Deformation Model

1. Introduction
In 1992, an Egyptian Survey Authority “ESA” steering committee developed a plan for the creation of new datum for Egypt, with the following approach [1] :
・ First, observing approximately 30 stations at approximately 200 km interval, covering all of Egypt, creating a High Accuracy Reference Network (HARN). Both high absolute and relative accuracies are required for these stations.
・ Second, establishing the Notational Agricultural Cadastral Network (NACN) relative to these 30 stations, covering the green area of Egypt (Nile Valley and the Delta) at 30 - 40 km intervals. This station spacing was selected to allow for further densification with single frequency receivers, see Figure 1.
・ Third, densifying this network at a station spacing of approximately 5 km for use as cadastral control at the governorate level.
・ Finally, replacing the existing Egyptian Mercator grid with a new modified UTM coordinate system.
Each station was observed for six sessions, every session was 6 hours with 30 seconds epoch interval. The observation time was planned to produce 1:10,000,000 (Order A) for HARN and 1:1,000,000 (Order B) for NACN relative network accuracy standard between stations. The results of analyzing both of them were defined in ITRF1994 Epoch 1996.
Many users of the geodetic system are non-technical users, for whom managing the dynamics of the datum represents a potential annoyance and complexity. ESA does not manage the dynamics of the geodetic system which enables other spatial datasets connected to it to be updated. The implementation of a “Continuously Operating Reference Stations (CORS)” network in Egypt in both ESA & NRIAG also represents a set of issues that need to be part of a semi-dynamic datum. This paper represents some of the implications and limitation for the users of geodetic and related datasets when implementing a semi-dynamic datum.
2. The Realization of International Terrestrial Reference Frame (ITRF)
The realization of International Terrestrial Reference System is named (conventional) Terrestrial Reference Frame (TRF) and it is carried out through the coordinates of a set of points on the earth serving as reference points. A conventional TRF is defined as a set of physical points with precisely determined coordinates in a specific coordinate system that is the realization of an ideal Terrestrial Reference System [2] . An example of TRF is the International Terrestrial Reference Frame (ITRF) introduced by the International Earth Rotation and Reference Systems Service (IERS), which is updated every year or several years (ITRF98, ITRF99, etc.). The key- element of the ITRF combinations is the availability of co-location sites where two or more space geodesy instruments are operating and where differential coordinates (local ties) between the measuring reference points of these instruments are determined [3] . Global Navigation Satellite Systems (GNSS) is able to provide all the
Figure 1. The HARN & NACN Networks.
necessary information of the datum definition of the Terrestrial Reference Frame (TRF) (origin, scale, and orientation), combination of reference frames provided by independent techniques has long been the standard method to implement global terrestrial reference frames.
3. Geodetic Datums
In the classical sense, a geodetic datum is a reference surface, generally an ellipsoid of revolution of adopted size and shape, with origin, orientation, and scale defined by a geocentric terrestrial frame. Once an ellipsoid is selected, coordinates of a point in space can be given in Cartesian or geodetic (curvilinear) coordinates (geodetic longitude, latitude, and ellipsoid height). Furthermore, the classical concept of geodetic datum implies that a datum’s coordinates are fixed and does not change with time except for the effect of local tectonic motion. Thus, the coordinate frame of a geodetic datum should be somewhat attached to the plate and move with it in such a way that the coordinates of the points will not change as a consequence of plate rotation.
3.1. Static Geodetic Datums
Two types of geodetic datum can be defined namely a static and kinematic geodetic datum. A static datum is thought of as a traditional geodetic datum where all sites are assumed to have coordinates which are fixed or unchanging with time. This is an incorrect assumption since the surface of the earth is constantly changing because of tectonic motion. The major limitation with a static geodetic datum arises from the ongoing divergence between ITRF and the fixed coordinates of a static geodetic network due to rigid plate motion. While the network may not necessarily be deforming internally to any significant degree, the lithospheric plate on which the network sits is moving as a rigid body over the Earth’s asthenospheric mantle. The impact of this deformation is noticeable where precision GNSS techniques are used to compute ITRF coordinates. Another limitation of a static datum arises from the processing of long GNSS baselines. If the static coordinates of a reference station are held fixed, rigid plate rotation of a long baseline will degrade the precision of the point computation as a function of time [4] .
To show the drawback of the currently used Egypt static datum, namely ITRF1994 Epoch 1996, the Helwan IGS Station with coordinate values computed by IGS computing center in ITRF2008 Epoch 2015.274, was transferred by the published transformation parameters to ITRF1994 Epoch 1996 (http://itrf.ign.fr/trans_para.php). The related Reference Frame coordinate values, related velocity parameters and the differences are tabulated in Table 1. As it is indicated in the table, the differences between Helwan coordinate values defined in ITRF2008 Epoch 2015 and the values defined in ITRF1994 Epoch 1996 are: −41.8 cm for X component, 26 cm for Y component and 31.6 cm for Z component. These discrepancies exceed any accuracy requirements needed by any control works.
3.2. Kinematic Geodetic Datums
A kinematic datum (also referred to as a dynamic datum in literature and practice) such as the latest realization of the International Terrestrial Reference Frame ITRF2008 [5] , is one where the coordinates of geodetic monuments on the Earth’s surface vary continuously as a function of time, relative to a geodynamically inert reference frame coupled with the Earth’s rotation. A Deformation Model (DM) enables kinematic coordinates in an
Table 1. The offset in Helwan coordinate values by using the static datum.
absolute geodetic reference frame such as ITRF to be propagated to a static reference epoch, a process described in this paper as “epochwise”, in order to distinguish it from classical kinematic conformal transformation methods such as the 14 parameter (7 parameters and their rates of change) Bursa-Wolf transformation [6] .
Global Navigation Satellite Systems (GNSS) inherently use an ITRF aligned reference frame for estimation of orbit ephemerides and derived positions of GNSS sensor locations. GNSS devices which use ITRF or closely aligned systems position users in agreement with the underlying kinematic frame. However, in practice there are a number of very significant drawbacks to a kinematic datum. Surveys undertaken at different epochs cannot be combined or integrated unless a deformation model is applied rigorously, or is embedded within the data, and the data are correctly time-tagged.
The limitations of a kinematic datum soon become apparent as kinematic and ground-fixed coordinates become misaligned. Kinematic coordinates increase the risk of litigation where legal definition of “fixed” coordinates is contested. They also increase the likelihood of errors in engineering surveys and damage to sub-surface infrastructure arising from misinterpretation or absence of epoch metadata.
3.3. Semi-Kinematic Geodetic Datum
A semi-kinematic datum is one where a deformation is modeled as an implicit component of the datum, thus enabling kinematic coordinates acquired by space geodetic techniques to be transformed consistently and accurately to a fixed reference epoch (static datum) over time. Many countries and regions which straddle major plate boundaries have adopted a semi-kinematic (or semi-dynamic) geodetic datum in order to prevent degradation of the datum as a function of time due to ongoing crustal deformation that is occurring within the country. The two major drivers for the adoption of a semi-kinematic datum in these countries have been:
・ The widespread adoption of precision GNSS techniques for surveying and positioning
・ The need to maintain consistency of coordinates to support combination and integration of spatial information acquired at different epochs [7] .
High precision GNSS positioning and navigation is very rapidly highlighting the disparity between global kinematic reference frames such as ITRF and WGS84, and traditional static geodetic datum. The disparity is brought about by the increasingly widespread use of PPP and the sensitivity of these techniques to deformation of the Earth due to plate tectonics.
4. The Requirements of Deformation Model
In order for surveys undertaken at different epochs to be combined or integrated within a kinematic datum, a deformation model has to be applied rigorously, or be embedded within the data. For the model to be applied correctly, all data has to be correctly time-tagged with the epoch of acquisition. A deformation model implies that the deformation is modeled with respect to an Earth-Centered Earth-Fixed (ECEF) reference frame consistent with the latest IERS Conventions, such as ITRF. A deformation model can be used to predict ITRF (absolute) site velocities at any location. The ITRF site velocity is then used to compute the displacement of the location between the epoch of measurement or acquisition and a reference epoch.
A deformation model can also be used for processing of long GNSS baselines by forward propagation of the ITRF coordinates of a CORS reference station from a reference epoch. This approach enables processing and network analysis to be accomplished wholly within ITRF thereby eliminating the effects of un-modeled plate rotation and deformation between the measurement and reference epochs. The deformation model can then be used in reverse propagation mode to compute the rover station coordinates at the reference epoch. A deformation model can be become an integral component of any semi-kinematic datum definition, with reference epoch (static) coordinates of the datum realized by epoch projection.
4.1. ITRF2008 Plate Motion Model (PMM)
In order to estimate a plate motion model consistent with ITRF2008, detailed analyses of the ITRF2008 velocity field were undertaken by [8] . Indeed, for various geodetic and geophysical applications of ITRF2008, the aim of the ITRF2008 Plate Motion Model was to provide users with the most precise plate motion model derived from and consistent with the ITRF2008. The analysis consisted in simultaneously estimating angular velocities for 14 plates, together with an origin rate bias of the selected velocity field of 206 sites (see Figure 3). The obtained results provide a model for 14 plates, with a global WRMS (Weighted Root Mean Scatter) of 0.3 mm/yr. The basic equation used for the estimation of plate angular velocities links the Euler vector 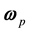 with point velocity
with point velocity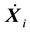 , of position vector Xi, located on plate p:
, of position vector Xi, located on plate p:
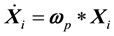
As it is shown in Table 2, Figure 2 and Figure 3, the number of sites (N.S.) in the Arab plates were just four sites, while for the Nubian plate the number of sites was 11, all of them were existed in the western and southern side of Nubian plate. The shortage of sites in the Middle East areas may affect the deformation model efficiency for this area. Hence, the need for an Egyptian Deformation Model is inevitable [9] .
Figure 2. The Green points of the final sites selected in and around Africa (Altamimmy et al., 2012).
Figure 3. ITRF2008 sites with time-span longer than three years with Green points of the 206 final sites selection.
Table 2. ITRF2008 PMM Absolute Plate Rotation Poles (Al-Timemmy et al. 2012).
4.2. The Egyptian Deformation Model
In 2006, NRIAG started the establishment of the Egyptian Permanent GPS Network (EPGN). Basically, the site selection was aimed to cover geographically all the Egyptian territory but also considering the tectonic setting of Egypt. As shown in Figure 4 three stations were located in the Eastern Desert at the Red Sea coast, two stations in Sinai Peninsula, three stations in the Western Desert, two stations at the Nile Valley, and six stations around Cairo and the Nile Delta. The EPGN operation started by four stations in 2007 to 15 stations was achievable at the end of 2011 (4 in 2007, 2 in 2008, 3 in 2010, and 6 stations in 2011). In addition to these 15 stations, which were established and administrated by NRIAG, there is a station in Alexandria organized by a French institute called Centre d’Études Alexandrines (CEALX), and in this work, it will be considered as one of the EPGN stations.
To calculate the velocity field referred to ITRF2008, in addition to the 16 EPGN stations [9] , they used 7 years data of 50 IGS stations starting from the beginning of 2006 to 30.09.2012 (day 274 in 2012). The selection of the IGS stations aimed to a good configuration around the EPGN for datum definition. The majority of these stations, 34 out of 50, are included in ITRF2008. The 50 selected IGS stations belong to 3 different plates, 29 stations on the African plate, 4 stations on the Arabian plate, and 17 stations on the Eurasian plate [9] .
4.3. Euler Plate Motion Parameters Estimation in the Deformation Model
To convert the aforementioned plate rotation rates, given by PMM in Table 2, about ITRS axes to Euler pole notation, the following equations should be used:
The Pole Rotation Rate can be computed by:
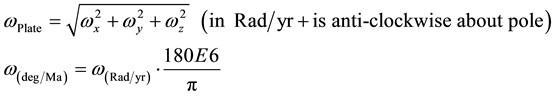 (1)
(1)
The Pole Latitude:
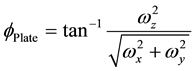 (2)
(2)
The Pole Longitude:
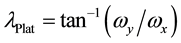 (3)
(3)
The velocity Estimation by PMM can be obtained by:
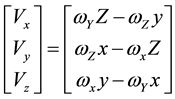 (4)
(4)
Table 3 outline the computed Euler Plate Motion Model Parameters for the ITRF2008 PMM based on Equations (1)-(3), on the other hand the related parameters were computed by [9] as shown in the table.
Figure 4. Geographic distribution of the Egyptian Permanent GPS Network (EPGN).
Table 3. Estimated Euler plate motion model parameters for the Nubian Plate.
4.4. Kinematic Transformation Parameters Using Rigid Plate Rotation Model
PPP, global RTK and GNSS post-processing services are now used extensively to provide realizations of ITRF and WGS84 globally with a precision of a few centimeters. Unless these instantaneous realizations are transformed to a static or semi-kinematic datum using a suitable deformation model, repeat surveys using these techniques will result in datum divergence as a function of time arising from the effects of un-modeled tectonic plate motion. Transformations from kinematic ITRF to a static datum are conventionally done by either using the site velocity (computed either from ITRF definition or from a plate motion model).
4.4.1. Firstly: The Classical “Displacement” Approach
a) Using Published IGS Displacement Values
The solution of CSRS-PPP SW is now used extensively to provide realizations of ITRF globally with a precision of a few centimeters. The CSRS-PPP’s service computes the absolute position for Helwan and Rabat, where both of them is considered as one of IGS stations that were used in computing the ITRF2008m IGS stations, at Epoch 2014.907 and Epoch 2015.324 respectively and the results are:
PPP solution for Helwan at ITRF2008 Epoch 2014.907
The published coordinates/standard deviations (95%) for the PHLW3310 RINEX file are as follow:
Latitude (ITRF08): 29 51 41.5732 dms/0.002 m, Longitude (ITRF08): 31 20 36.2409 dms/0.004 m, Ellipsoidal Height (ITRF08): 148.729 m/0.009 m Cartesian coordinates (X Y Z in meters) à 4,728,141.193, 2,879,662.605, 3,157,147.146
PPP solution for Rabat at ITRF2008 Epoch 2015.324
The published coordinates/standard deviations (95%) for the rabt1000 RINEX file are as follow:
Latitude (ITRF08): 33 59 53.1790 dms/0.003 m, Longitude (ITRF08): −6 51 15.4350 dms/0.006 m, Ellipsoidal Height (ITRF08): 90.086 m/0.013 m Cartesian coordinates (X Y Z in metres) à 5,255,617.590, −631,745.508, 3,546,322.700
The coordinates of the HELWAN and RABAT stations at ITRF2008 reference epoch (t0 = 2005) were published by IGS at http://itrf.ensg.ign.fr/site_info_and_select/solutions_extraction.php, and given in Table 4.
To transfer the Helwan and Rabat coordinates to be in ITRF2008 at the Epoch 2014.907 and 2015.324, the approach represented by Equation (5) can be applied:
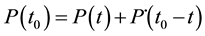 (5)
(5)
where:
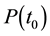 is the positioning at a reference epoch ITRF 2008 Epoch 2005
is the positioning at a reference epoch ITRF 2008 Epoch 2005


The transferred coordinates of the updated Helwan and Rabat stations are tabulated in Table 5. The differences between the PPP computed values and the IGS published values are also given in the same table. As it is indicated in Table 5, the differences between the PPP-solution for Helwan are in the ranges of 5 - 9 cm and for Rabat the differences are just in the range of ± 2 mm.
b) Using Egyptian DM Values in the Displacement Approach
To see how the Egyptian DM can be used in the displacement approach, the following comments should be considered:
§ In the displacement approach, the geocentric cartesian (XYZ) coordinates is always used, so the need for
Table 4. IGS solution for Helwan and Rabat at ITRF2008 Epoch 2005.
Table 5. The updated positioning for Helwan defined in ITRF2008 Epoch 2014.907 and Rabat defined in ITRF2008 Epoch 2015.324by IGS & PPP.
XYZ velocities is a must, namely VXYZ;
§ The Egyptian deformation model, the velocity is given in topocentric (ENU), namely Venu;
§ To convert between the geocentric to topocentric velocities, rotation matrix, for the point’s latitude (φ) and longitude (λ) can be used:



By applying the above equation for Helwan and Rabat we get the following the results using Egyptian DM in the displacement approach.
For Helwan 

For Rabat 

To evaluate the computed velocity Vxyz of both Deformation Models, we transfer the coordinate values of Helwan and Rabat defined in ITRF2008 Epoch 2014.901 & 2015.324 to be compared with the published values of IGS defined in ITRF2008 Epoch 2005, given in Table 4. By applying Equation (5), the following results, given in Table 6, were obtained.
As it is depicted in Table 6, the differences between the converted PPP-solution at epoch t = 2005 for Helwan computed by the Egypt DM are in the ranges of 5.9 - 7 cm, which is better than the results by the displacement (classical) approach of ITRF2008 Table 5. On the other hand, the Egypt DM output differences for Rabat in the range of −3 mm to 29 mm worth than the ITRF2008 PMM. This result confirms that the computed Egypt DM is valid only in Egypt.
In case of the transformation between two epochs defined in two different reference frames, the following model can be used in the transformation process:

Table 6. The updated positioning for Helwan & Rabat defined in ITRF2008 Epoch 2005 Using velocities computed from deformation model.
and
where:





4.4.2. Secondly: The Euler Angle Velocity Approach
Rigid Plate movement is conventionally defined by a rotation rate about an Euler Pole 












Equations (10)-(12) were used to compute (ΩX, ΩY, ΩZ) for the Nubian Plate using the Euler parameters determined by ITRF2008 PMM & Egypt’s Deformation Model, the results were depicted in Table 7.
A site velocity in Cartesian format 
By introducing a reference epoch 







Bu using Equation (13) for Helwan & Rabat and the computed angular velocity for Egypt DM & PMM, given in Table 7, the converted coordinates for both stations defined in ITRF2008 Epoch 2005 by the Cartesian Angular Velocity of Local & ITRF2008 Deformation Model can be obtained. Computation details for Helwan are given in the next two equations and the results are tabulated in Table 8.
Table 7. The cartesian angular velocity of nubian plate.
Table 8. The results of the Cartesian angular velocity of Local & ITRF2008 Deformation Model for Helwan& Rabat.
For Egypt Euler Parameters:
For PMM Euler Parameters:
As it is demonstrated in Table 8, the differences between the converted PPP-solution at epoch t = 2005 for Helwan computed by the Egypt DM and PMM are approaching each other, which is better than the results by the displacement approach of ITRF2008. On the other hand, the Egypt DM output differences for Rabat in the range of −12 mm to 15 mm, and −10 mm to 6.5 mm for ITRF2008 PMM. This result confirms the computed Egypt DM is more suitable for Egypt.
The above equation can also be used to realize a static geocentric datum aligned with ITRF at a specific reference epoch. Instantaneous ITRF positions measured at different locations and at different epochs on the same rigid plate can be related to the static datum at the reference epoch by using the same parameters (





The above equations are accurate within rigid plate zones, however within deforming zones additional parameters derived from deformation models (e.g. Finite Element Model and Fault Locking models) are required in order to maintain consistency between different epochs [10] . In addition, co-seismic and post seismic terms need to be added. For any location on a rigid plate, instantaneous ITRF coordinates can be transformed to a fixed reference epoch using equation (15) [11] (Stanaway and Roberts, 2009).

where:






5. Conclusions
PPP, global RTK and GNSS post-processing services are now used extensively to provide realizations of ITRF and WGS84 globally with a precision of a few centimeters. Unless these instantaneous realizations are transformed to a static or semi-kinematic datum by using a suitable deformation model, repeat surveys using these techniques will result in datum divergence as a function of time arising from the effects of un-modeled tectonic plate motion. Transformations from kinematic ITRF to a static datum are conventionally done by either using the site velocity (computed either from ITRF definition or from a plate motion model).
To avoid the discrepancies between the currently used datum for Egypt, namely ITRF1994 Epoch 1996, and On-Line GNSS Services, a semi-kinematic datum and related deformation models were applied and tested for Egypt. The results of some point samples show that the local Deformation Model for Egypt is giving less discrepancy than the most recent published velocities of ITRF2008 and ITRF2008 PMM. The results also confirm that the PMM model is giving good performance for the other parts out of Egypt.
Cite this paper
MostafaRabah,AhmedShaker,MagdaFarhan, (2015) Towards a Semi-Kinematic Datum for Egypt. Positioning,06,49-60. doi: 10.4236/pos.2015.63006
References
- 1. Scott, M. (1997) Results of Final Adjustment of New National Geodetic Network. Geodetic Advisor for the Egyptian Survey Authority.
- 2. Boucher, C. and Altamimi, Z. (2001) ITRS, PZ-90 and WGS 84: Current Realizations and the Related Transformation Parameters. Journal of Geodesy, 75, 613-619.
http://dx.doi.org/10.1007/s001900100208 - 3. Altamimi, Z. (2002) Discussion on How to Express a Regional GPS Solution in the ITRF. Institute Geographique National (IGN), Ecole Nationale des Sciences Geographiques, Marne la Value Cedex.
- 4. Dawson, J., and Woods, A. (2010) ITRF to GDA94 Coordinate Transformations. Journal of Applied Geodesy, 4, 189- 199.
http://dx.doi.org/10.1515/jag.2010.019 - 5. Altamimi, Z., Collilieux, X. and Metivier, L. (2011) ITRF2008: An Improved Solution of the International Terrestrial Reference Frame. Journal of Geodesy, 85, 457-473.
http://dx.doi.org/10.1007/s00190-011-0444-4 - 6. Stanaway, R., Roberts, C. and Blick, G. (2012) Realization of a Semi-Kinematic Geodetic Datum Using an Absolute Deformation Model (ADM). School of Surveying and Spatial Information Systems, University of New South Wales, Sydney.
- 7. Pearson, C., McCaffrey, R., Elliott, J. and Snay, R. (2010) HTDP 3.0: Software for Coping with the Coordinate Changes Associated with Crustal Motion. Journal of Surveying Engineering, 136, 80-90.
http://dx.doi.org/10.1061/(asce)su.1943-5428.0000013 - 8. Altamimi, Z., Métivier, L. and Collilieux, X. (2012) ITRF2008 Plate Motion Model. Journal of Geophysical Research, 117, B07402.
http://dx.doi.org/10.1029/2011jb008930 - 9. Saleh, M. and Becker, M. (2013) A New Velocity Field from the Analysis of the Egyptian Permanent GPS Network (EPGN). Arabian Journal of Geosciences, 7, 4665-4682.
- 10. Dow, J.M., Neilan, R.E. and Rizos, C. (2009) The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems. Journal of Geodesy, 83, 191-198.
http://dx.doi.org/10.1007/s00190-008-0300-3 - 11. Stanaway, R. and Roberts, C. (2009) A Simplified Parameter Transformation Model from ITRF2005 to Any Static Geocentric Datum (e.g. GDA94). Proceedings from International Global Navigation Satellite Systems Society IGNSS Symposium 2009, Surfers Paradise, 1-3 December 2009.










