Positioning
Vol.2 No.2(2011), Article ID:5054,9 pages DOI:10.4236/pos.2011.22010
An Integrated Air Data / GPS Navigation System for Helicopters
![]()
1ROTAM Center, Istanbul Technical University, Maslak, Istanbul,Turkey; 2Faculty of Aeronautics & Astronautics, Istanbul Technical University, Maslak, Istanbul, Turkey.
Email: tanermutlu@rotam.itu.edu.tr, cingiz@itu.edu.tr
Received April 29th, 2011; revised May 12th, 2011; May 18th, 2011.
Keywords: Integrated Navigation Systems, Air Data System, Global Positioning System, Complementary Kalman Filter.
ABSTRACT
In this study, the integration of two navigation systems Air Data System (ADS) and Global Positioning System (GPS) was aimed. ADS is a widely used navigation system which measures static and total air pressure and the air temperature. ADS has high sampling frequency and poor accuracy, on the other hand, another navigation system GPS has high accuracy compared to ADS but lower sampling frequency.Kalman Filter is used to integrate and minimize the errors of the two navigation systems. By this integration a navigation system with high sampling frequency and high accuracy is aimed. Another object is to calculate the wind speed with high accuracy.
1. Introduction
Navigation is the process of determining significant position, velocity, attitude, and time (PVAT) information relative to specified references. Guidance is the process of using navigation information to steer or maneuver in an intelligent way. Three types of navigation came to these days: celestial navigation, deduced reconnaissance, (commonly called dead reckoning), and pilotage. Today, modern airborne navigation systems are classified as either autonomous or position fixing, passive or active, stand-alone or aided, analog or digital.
An autonomous passive system, such as an inertial guidance system, provides reasonably accurate instantaneous PVAT output with no dependence on any external man-made device or signal; that is, it is neither jammable nor capable of being sensed from outside the vehicle. Stand-alone navigation systems, on the other hand, usually require externally provided electro magnetic signals from ground-based radio navigation aids (NAVAIDS) or from space-based satellites. Integrated navigation systems combine the best features of both autonomous and stand-alone systems and are not only capable of good short-term performance in the autonomous or stand-alone mode of operation, but also provide exceptional performance over extended periods of time when in the aided mode. Integration thus brings increased performance, improved reliability and system integrity, and of course increased complexity and cost [1]. Moreover, outputs of an integrated navigation system are digital, thus they are capable of being used by other resources of being transmitted without loss or distortion. The new century’s improvements in computer technology, and increased data processing rates brought the ability to improve the navigation systems of air vehicles in precision, correctness and reliability.
In the paper [2] integrated navigation system issue has been discussed. In the paper it is stated that, with the demand from the aviation industry, Instrumental Landing Systems (ILS) tend to be improved. This could not only be through replacement with the Microwave Landing System (MLS), but also by integrating Global Positioning System to the ILS that is practically in service.
In the paper [3] development of a Kalman filter for optimal combination of GPS, INS and Radar Altimeter data is presented. Due to the paper, being two independent navigation systems, GPS and INS have their own shortcomings when used in a stand-alone mode. The evergrowing drift in position accuracy of the INS, and the possible unavailability of the GPS signals are discussed. The author suggests that, these shortcomings would be eliminated, and each system’s best performances combined through the Kalman filter.
The benefits of integrating GPS with a strapdown INS are significant. However, altitude accuracy can further be improved by integrating the GPS, baro-inertial loop aided strapdown INS, and radar altimeter data. An error model of the strapdown INS plays an important role in the development of a Kalman filter for optimal combination of navigation data provided by GPS, strapdown INS and radar altimeter. Integrating the error models of each system with the use of the Kalman filter simulates this. The simulation results show an undeniable improvement in the demanded properties. The approach, tools and the data are identical to the ones in this study and the results are somehow in the same manner [3].
There have been many studies on integrated navigation systems. However, a few studies where both Air Data System and GPS had been used to obtain better navigation has been found in the literature. In [4] GPS is used to calibrate the inaccurate Air Data measurements. However the GPS samples are used to calibrate the ADS samples one-to-one. In the mentioned study no filtering approach has been used to minimize the error.
In this work, it is aimed to obtain an integrated ADS/GPS navigation system for helicopters which has high measurement frequency and high accuracy. Another objective is to calculate the wind speed with high accuracy.
2. Complementary Kalman Filter Based Integrated ADS/GPS Navigation System to Helicopter Dynamics
To integrate two navigation sources a Complementary Kalman Filter will be used here. Namely instead of system state variable estimates, the system’s error estimates will be obtained by the Kalman Filter.
As seen in Figure 1 the difference of speeds obtained from each navigation system is introduced into the Kalman Filter. And the Kalman Filter outputs the Air Data System speed and position error estimate values. ![]() ,
,![]() ,
,![]() are the airspeed values in cartesian coordinates. These values are obtained by transformation of total airspeed, angle of attack and angle of sideslip measurements. The information we need for this filtering process are the system error models and the measurement error model. The system error vector with required parameters is as follows:
are the airspeed values in cartesian coordinates. These values are obtained by transformation of total airspeed, angle of attack and angle of sideslip measurements. The information we need for this filtering process are the system error models and the measurement error model. The system error vector with required parameters is as follows:
 (1)
(1)
Here the 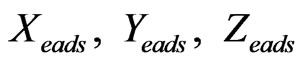 are the position errors of Air Data System and
are the position errors of Air Data System and 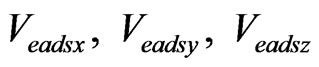 are the speed errors of Air Data System, each in cartesian coordinates. In the Air Data System the True Air Speed error is mainly the result of the wind speed. Therefore choosing the Air Data System errors as the vector parameters shown in Figure 1, is for the purpose of obtaining the true air speed error, which is relatively high, and thus the wind speed. The uncorrelated model, which is used in exponential correlation function for the stagnant processes will be used ([5-8]). This expression is in discrete and matrix form and is very suitable for simulation [7]:
are the speed errors of Air Data System, each in cartesian coordinates. In the Air Data System the True Air Speed error is mainly the result of the wind speed. Therefore choosing the Air Data System errors as the vector parameters shown in Figure 1, is for the purpose of obtaining the true air speed error, which is relatively high, and thus the wind speed. The uncorrelated model, which is used in exponential correlation function for the stagnant processes will be used ([5-8]). This expression is in discrete and matrix form and is very suitable for simulation [7]:
where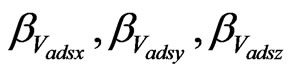 are the variables which are inverse to true air speed correlation time and
are the variables which are inverse to true air speed correlation time and  are the Gaussian distributed noises of the Air Data System speed measurements,
are the Gaussian distributed noises of the Air Data System speed measurements, 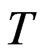 is the sampling period.
is the sampling period.
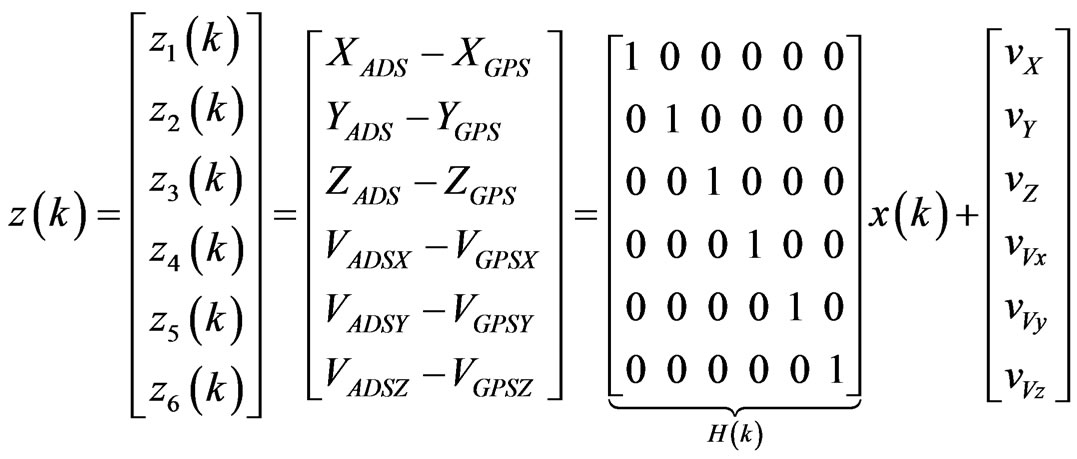
Using the Air Data System and GPS speed measurement differences as measurements observation vector in the Kalman Filter, the observation vector can be stated as:
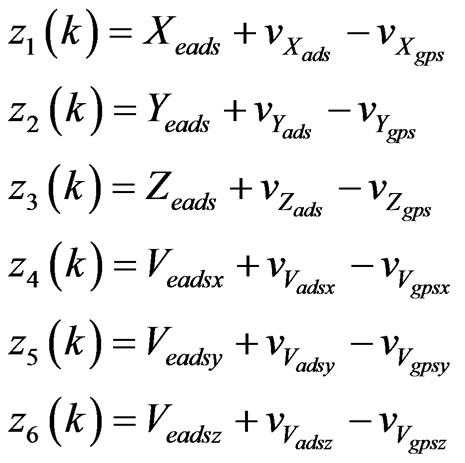 (3)
(3)
Here  are the true air speed measurement errors of the Air Data System and at the same time are the wind speeds and
are the true air speed measurement errors of the Air Data System and at the same time are the wind speeds and 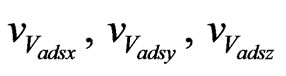 and
and
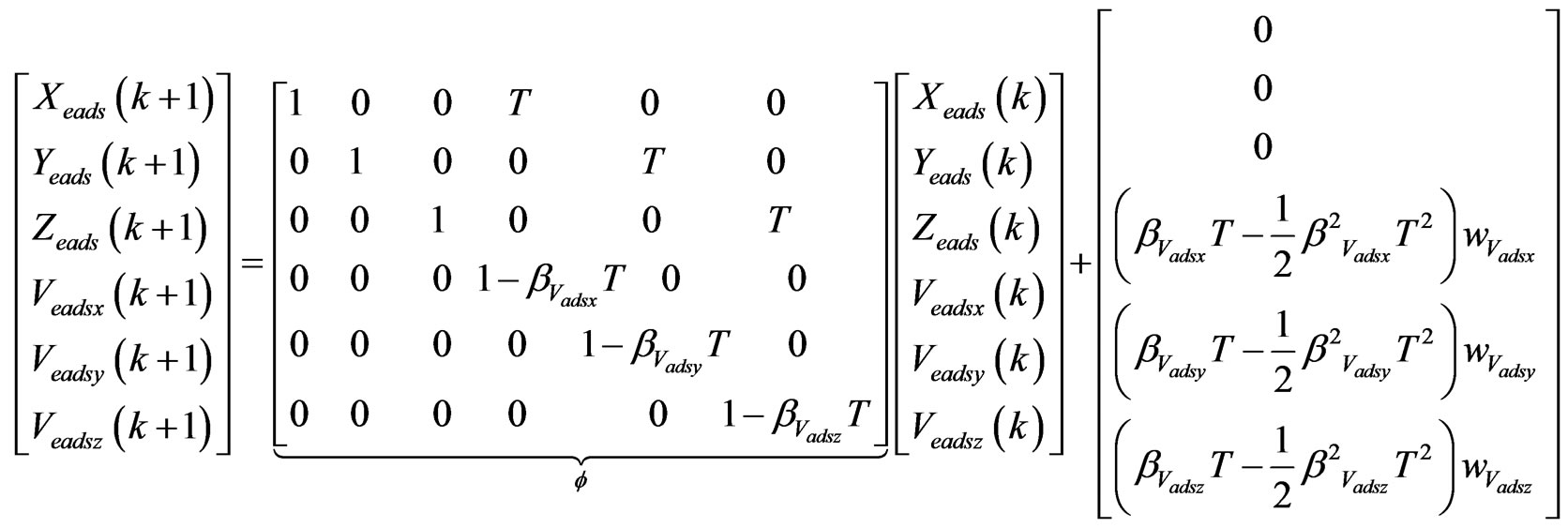 (2)
(2)
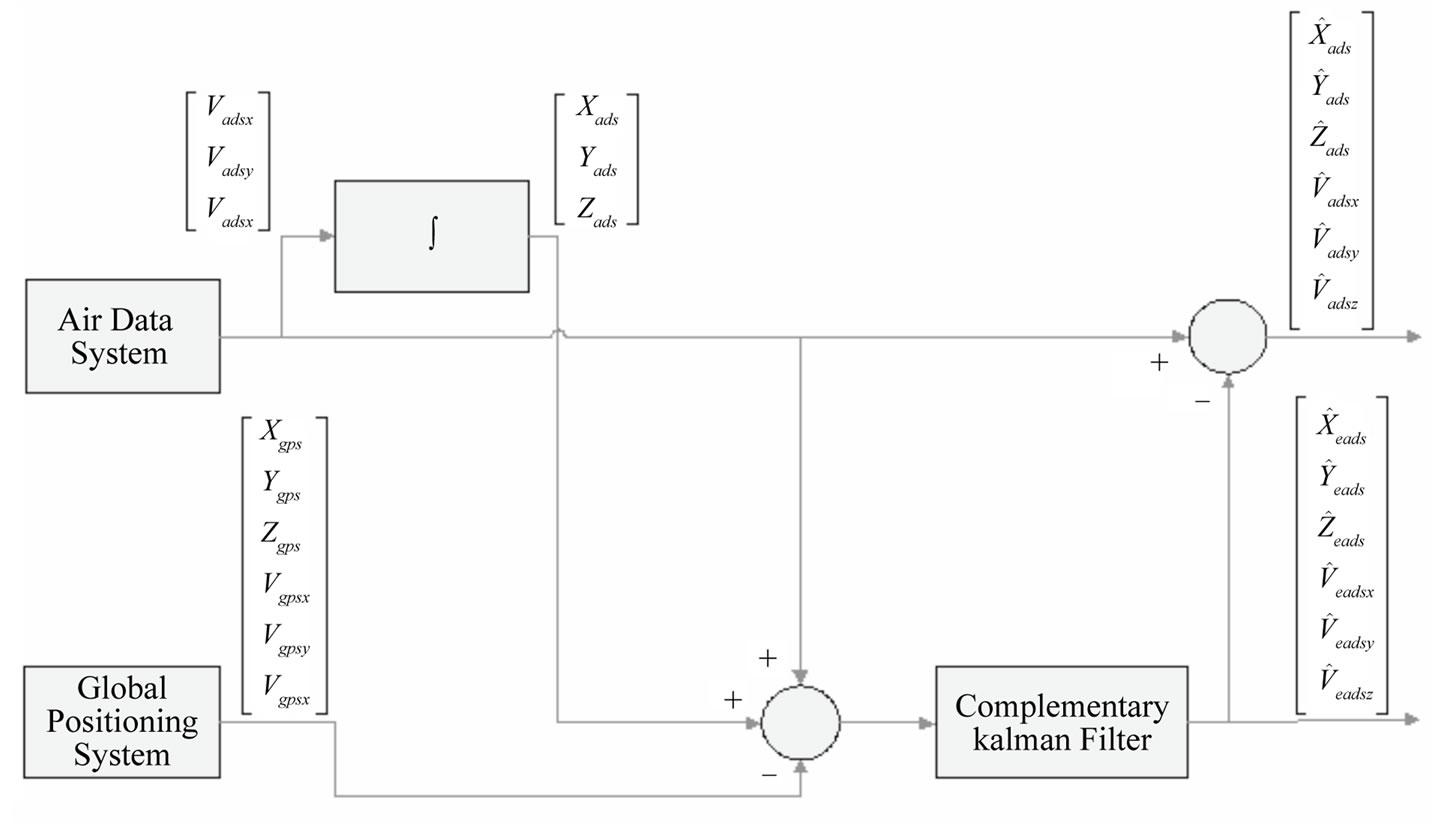
Figure 1. Integration of air data system and GPS.
 are the zero-mean Gaussian measurement noises of the Air Data System and GPS respectively. Namely, the difference between the GPS speed measurement and the Air Data System true air speed measurement gives us the Air Data System speed error and the wind speed during flight. However, this wind speed information includes the random noises of both systems. Measurement statements of (3) are written in matrix form:
are the zero-mean Gaussian measurement noises of the Air Data System and GPS respectively. Namely, the difference between the GPS speed measurement and the Air Data System true air speed measurement gives us the Air Data System speed error and the wind speed during flight. However, this wind speed information includes the random noises of both systems. Measurement statements of (3) are written in matrix form:
To obtain the Air Data System true error values that will be used in the simulation, the system error model is used;
 (5)
(5)
And solving (5) according to the initial values the true error values are obtained. Here ![]() is the transition ma-trix of the system error model which describes the evolution of the system error. The system’s error vector for the true error values is;
is the transition ma-trix of the system error model which describes the evolution of the system error. The system’s error vector for the true error values is;
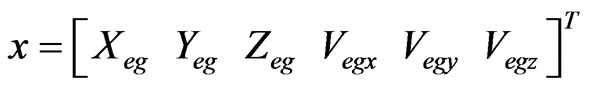 (6)
(6)
The Air Data System and GPS is integrated using the following Optimal Kalman filter:
Here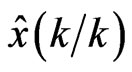 is the estimation value, I is the unity matrix, K(k)is the gain matrix of Kalman filter, P(k,k) is the correlation matrix of estimation error, P(k,k-1) is the correlation matrix of extrapolation error, H(k) is the measurement matrix,
is the estimation value, I is the unity matrix, K(k)is the gain matrix of Kalman filter, P(k,k) is the correlation matrix of estimation error, P(k,k-1) is the correlation matrix of extrapolation error, H(k) is the measurement matrix,  is the innovation process, Q(k-1) is the correlation matrix of system noise, G is the system noise transition matrix.
is the innovation process, Q(k-1) is the correlation matrix of system noise, G is the system noise transition matrix.
Initial conditions are shown below:
 (4)
(4)
 (7)
(7)
 (8)
(8)
x(0) and P(0) the initial conditions known a prior, correlation matrix of system noise Q(k) and correlation matrix of measurement error R(k) are necessary beforehand, in order the Kalman filter work.
The data necessary for this filtering application is the system’s error model and the observation’s error model.
As seen in Figure 1, the output of the Kalman Filter gives air data system speed error estimates which is wind speed estimates  and connected with these, the position error estimates
and connected with these, the position error estimates ,
,  ,
,  are obtained. Subtracting these error values from the measured speed values of the Air Data System the estimated flight speeds
are obtained. Subtracting these error values from the measured speed values of the Air Data System the estimated flight speeds 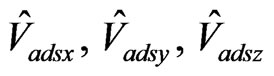 are obtained, and subtracting the Kalman Filter estimated position error from measured true positions, we obtain the position estimates:
are obtained, and subtracting the Kalman Filter estimated position error from measured true positions, we obtain the position estimates: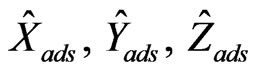 . The ground speed estimates can be written as:
. The ground speed estimates can be written as:

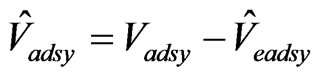
 (9)
(9)
The position estimates are as follows:
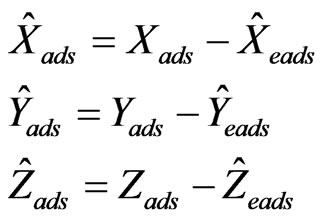 (10)
(10)
3. Application of Integrated ADS/GPS to Helicopter Flight Dynamics
The equations of helicopter motion that will be used in the flight dynamics simulation are [9]:
 (11)
(11)
Here x is the vector that contains the state variables, y is called the output vector, u is the control or input vector, A is the state matrix, B is the input matrix or control matrix, C is the output matrix, and D is the feedforward matrix. Combining the longitudinal and lateral flight dynamics equations of motion in a single matrix form, we obtain:
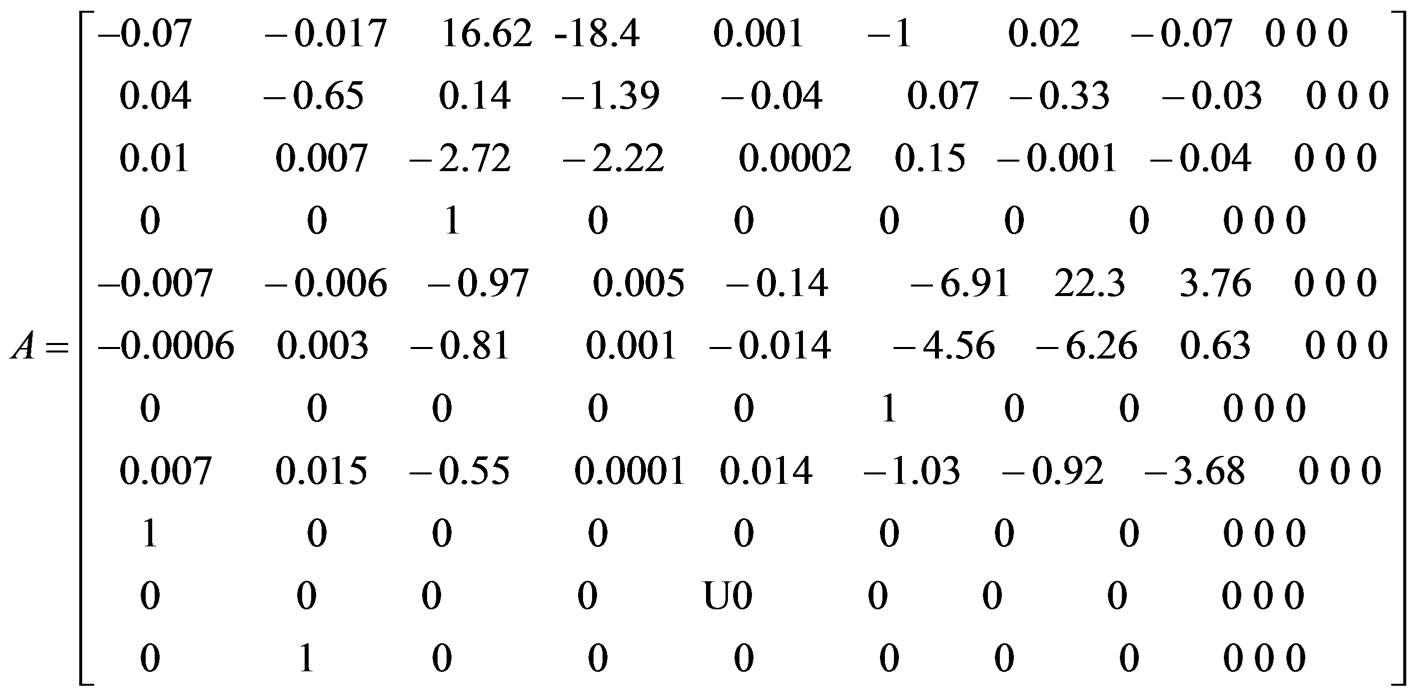
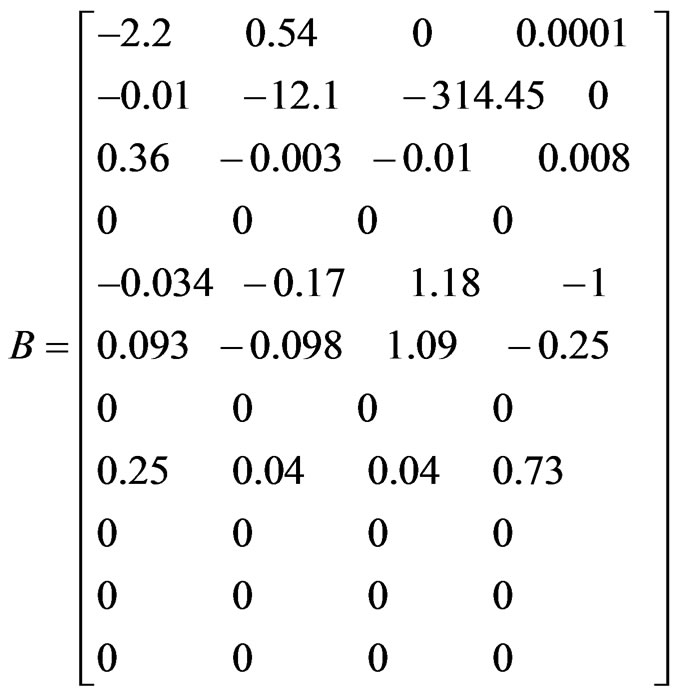 (12)
(12)
The state vector including the flight state variables is:
 (13)
(13)
The variables in the state vector are:
u: flight speed in direction X(m/sec)
w: flight speed in direction Z(m/sec)
q: pitch angular speed(degree/sec)
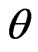 : pitch angle(degree)
: pitch angle(degree)
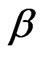 : yaw angle(degree)
: yaw angle(degree)
 : roll angle(degree)
: roll angle(degree)
p: roll angular speed(degree/sec)
r: yaw angular speed(degree/sec)
X, Y, Z: the position coordinates(m)
Using equations (11) - (13) of flight dynamics, we calculate the changes of the values of the state vector. In the simulation the discrete-time form is used. The C matrix is a [11 × 11] unity matrix and the D matrix is assumed zero.
True airspeed standard deviations on x,y,z axes are assumed:
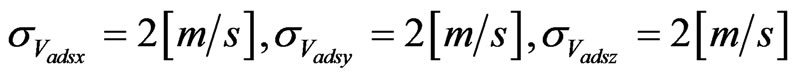
GPS ground speed standard deviations are taken

Air data system speeds correletaion times inverses are [10]:
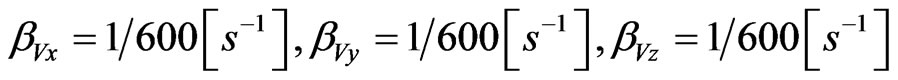
Sampling time is taken T = 0.001[Section] in the simulation. System transition matrix in discrete form:
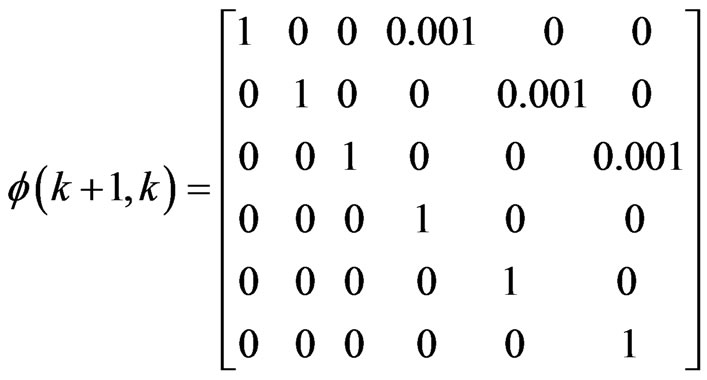 (14)
(14)
Correlation matrix of initial values is follows:
 (15)
(15)
The measurement matrix H from expression (4) and the system noise transition matrix G, are 6 × 6 dimension identity matrices. System noise correlation matrix Q(k) and measurement error correlation matrix R(k) are taken as
 (16)
(16)
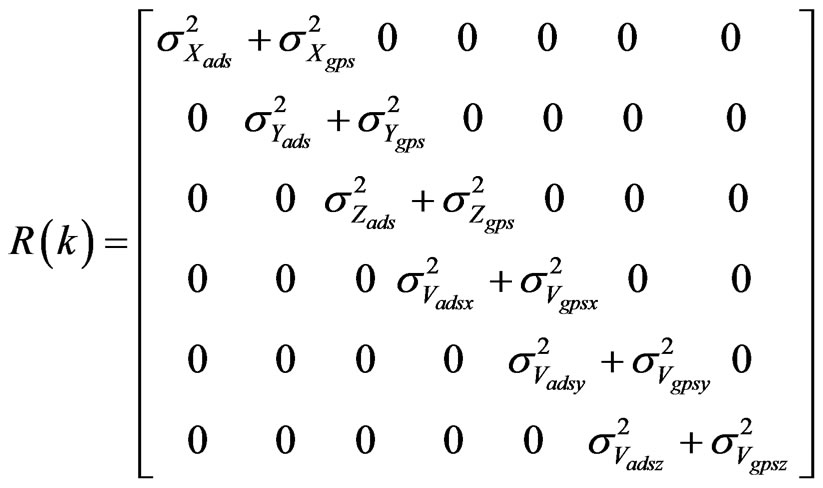 (17)
(17)
Measurement error correlation matrix is a diagonal matrix, with the sum of the random measurement variances of Air Data System and those of GPS composing the diagonal elements.
After executing MATLAB code including the Kalman Filter the following (see Figures 2-8) are obtained.
In Figures 2 - 7 the straight lines indicate true position and speed values. The position and speed error estimates for all state variables obtained by the Kalman filter, are very close to the actual position and speed errors. This convergence is present in all iterations. The differences of position and speed of two measurement systems is applied to the Kalman Filter. As a result position and speed errors of the Air Data System is calculated by the Kalman Filter. Small position and speed errors of the GPS has not been included to the state variables. True air speed errors obtained by the Kalman Filter provides the wind speeds. In Figure 2 the measurement value, actual value, and estimated value of the wind speed in the X direction are shown. As seen, the estimated air speed error converges closely to the actual air speed error. Air speed error calculated by the Kalman Filter is approximately 0.2 m/s and is superior to the noisy measurement values. In Figure 8 position and speed error estimate variances obtained from P(k/k) correlation matrix are shown. In this figure the error estimate variances’ convergence to zero can be seen. In Figures 5 - 7 the X, Y, Z directions position error estimates and actual errors and differences between them are shown. In these figures the relatively large initial error is regularly decreasing. The Y, Z directions speed error estimates and true errors and differences between them are shown in Figures 3 - 4.
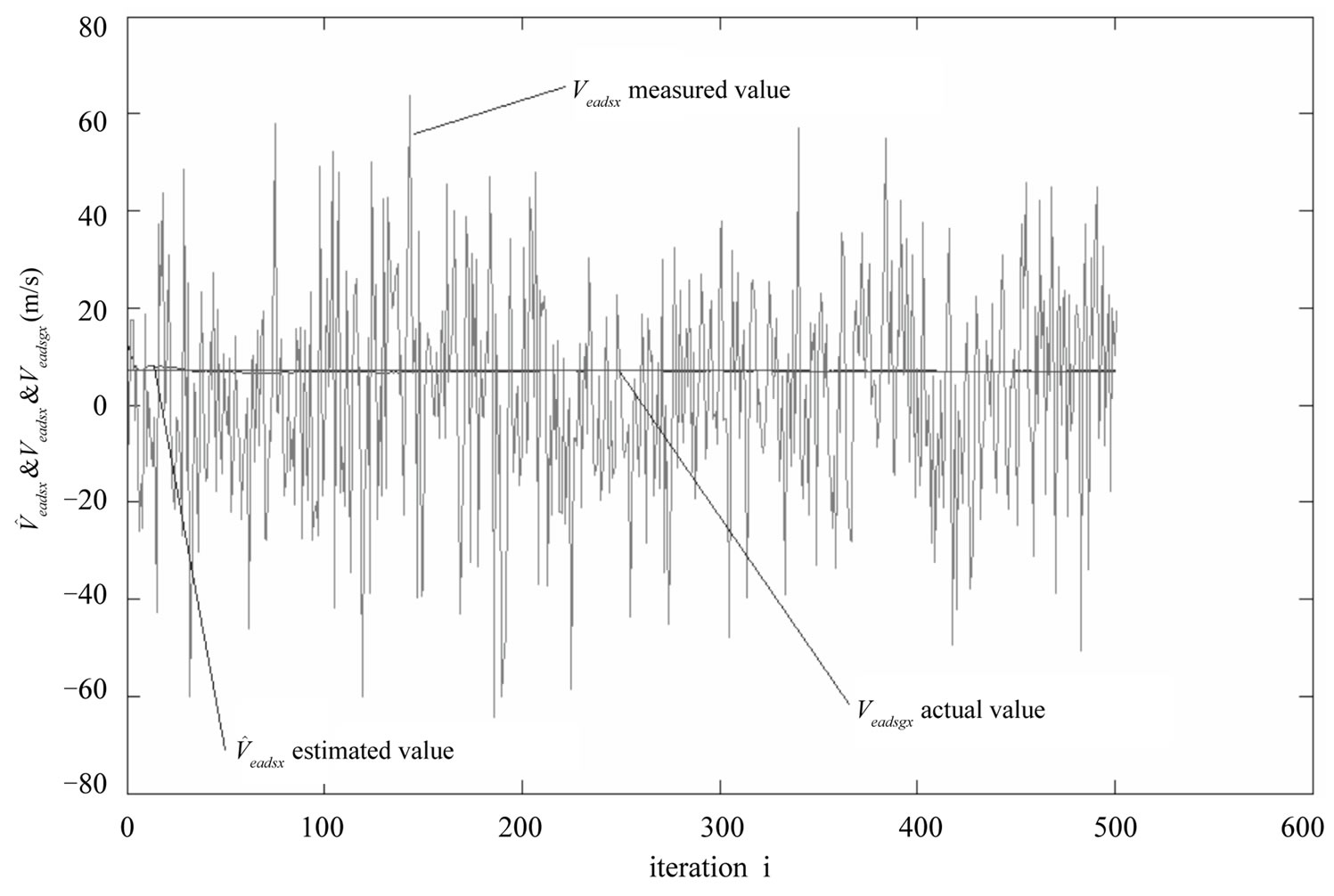
Figure 2. Measurement value (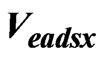 ), actual value (
), actual value (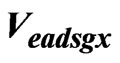 ), and estimated value (
), and estimated value ( ) of wind speed in X direction.
) of wind speed in X direction.
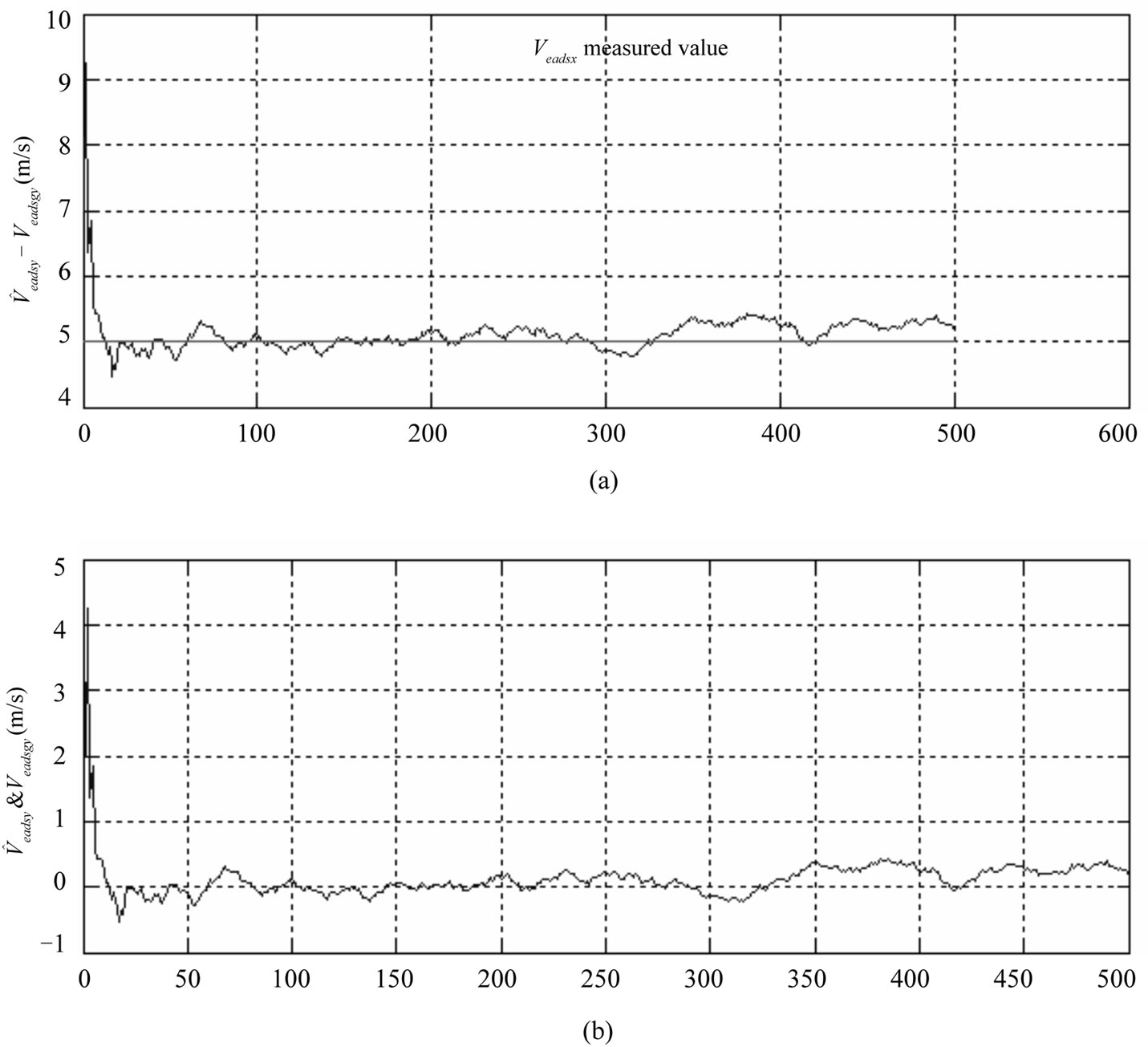
Figure 3. Y speed error estimate( ) and actual error(
) and actual error(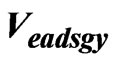 )(a) and differences between them(b).
)(a) and differences between them(b).
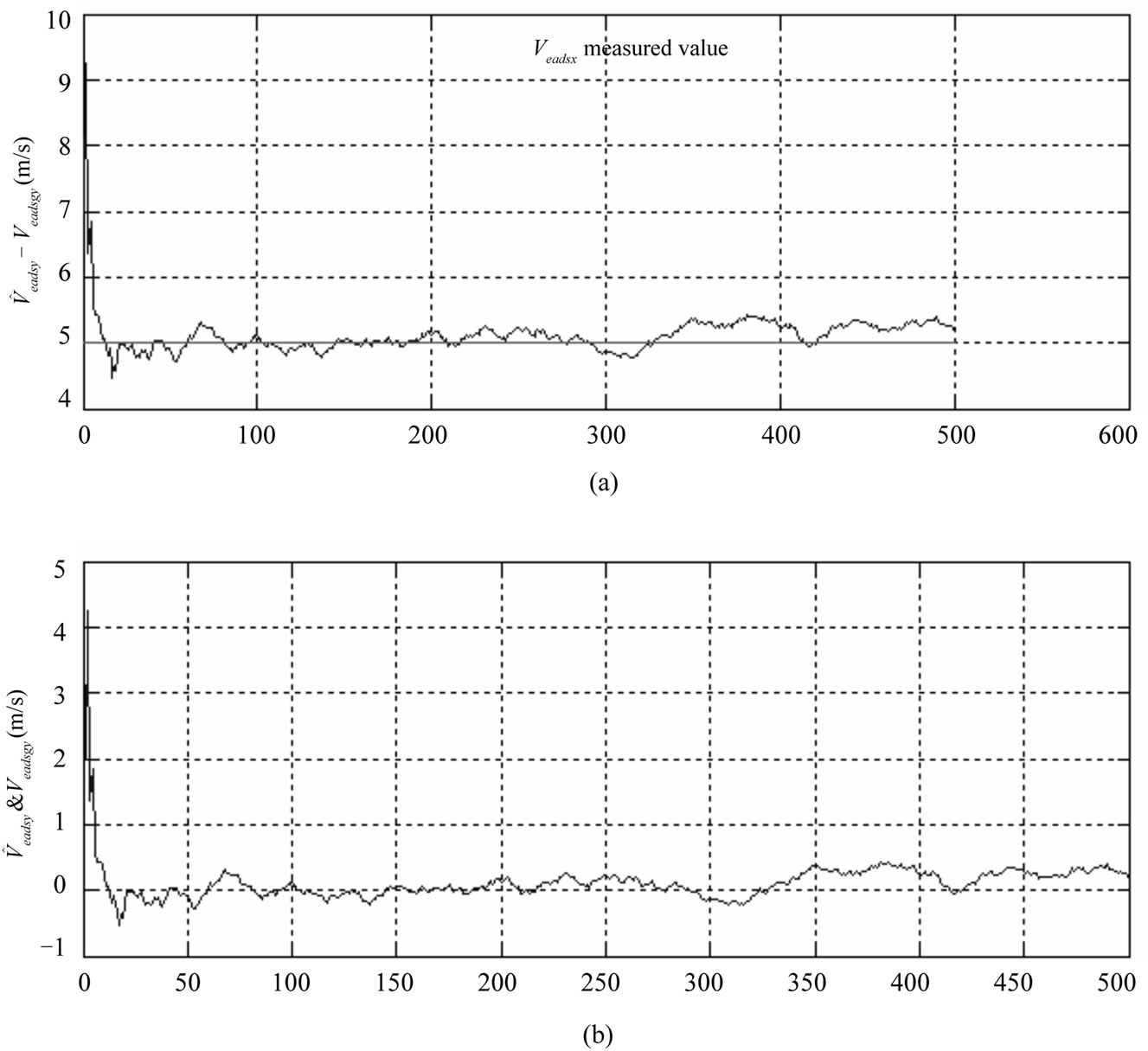
Figure 4. Z speed error estimate ( ) and actual error (
) and actual error (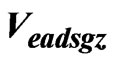 )(a) and differences between them(b).
)(a) and differences between them(b).
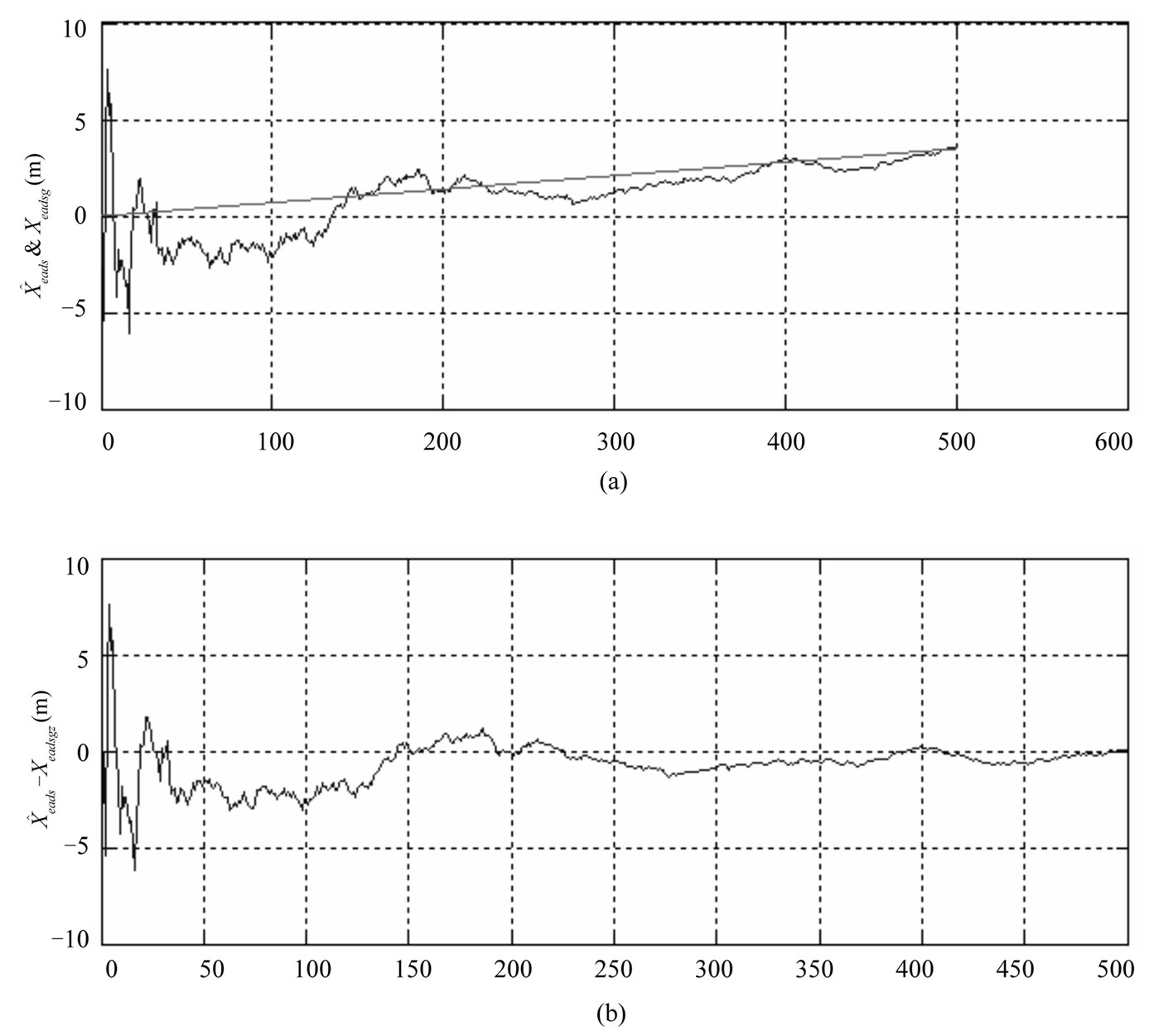
Figure 5. X position error estimate (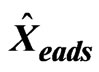 ) , actual error (
) , actual error ( ) (a) and differences between them(b).
) (a) and differences between them(b).
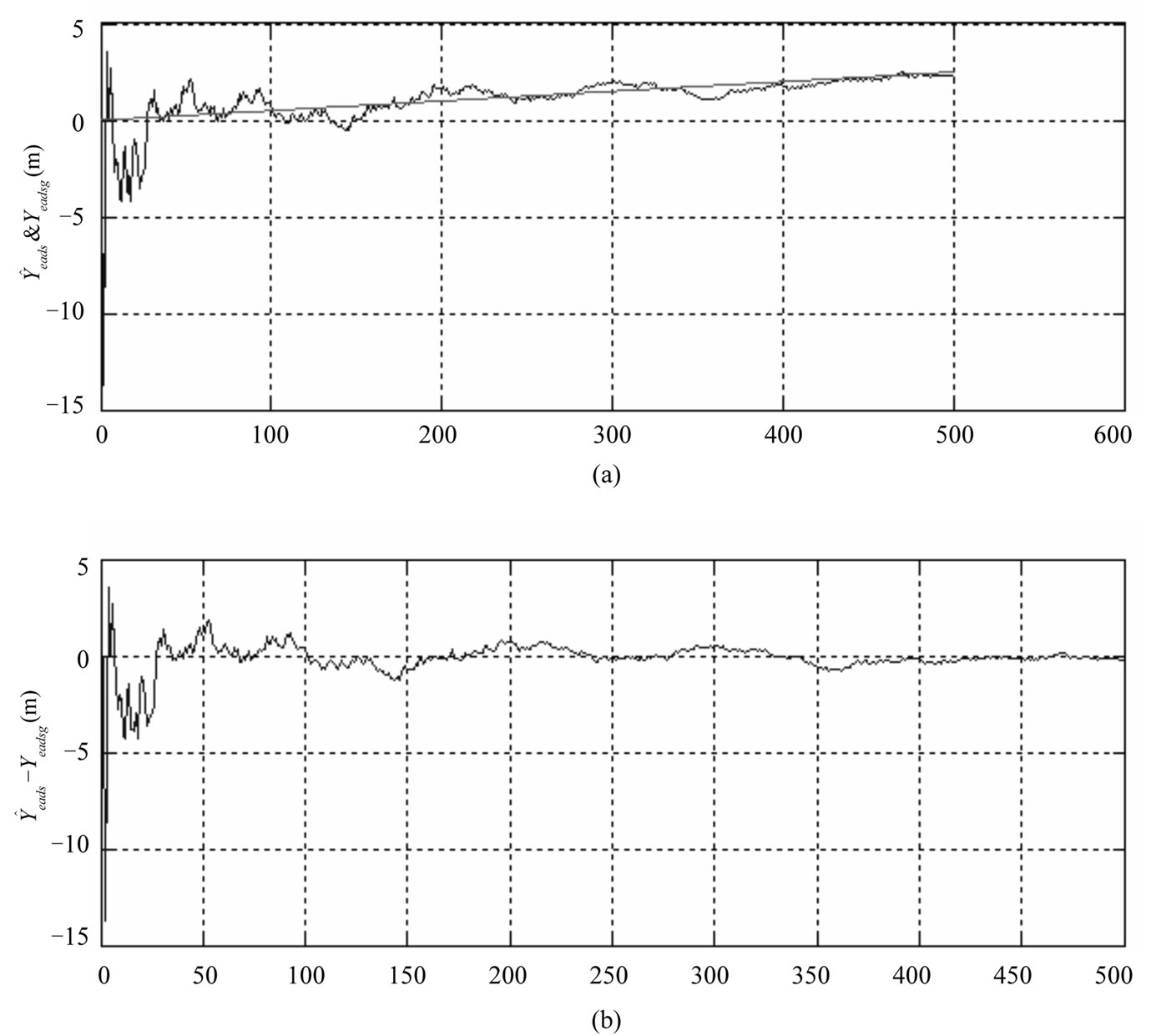
Figure 6. Y position error estimate( ) and actual error(
) and actual error( )(a) and differences between them(b).
)(a) and differences between them(b).
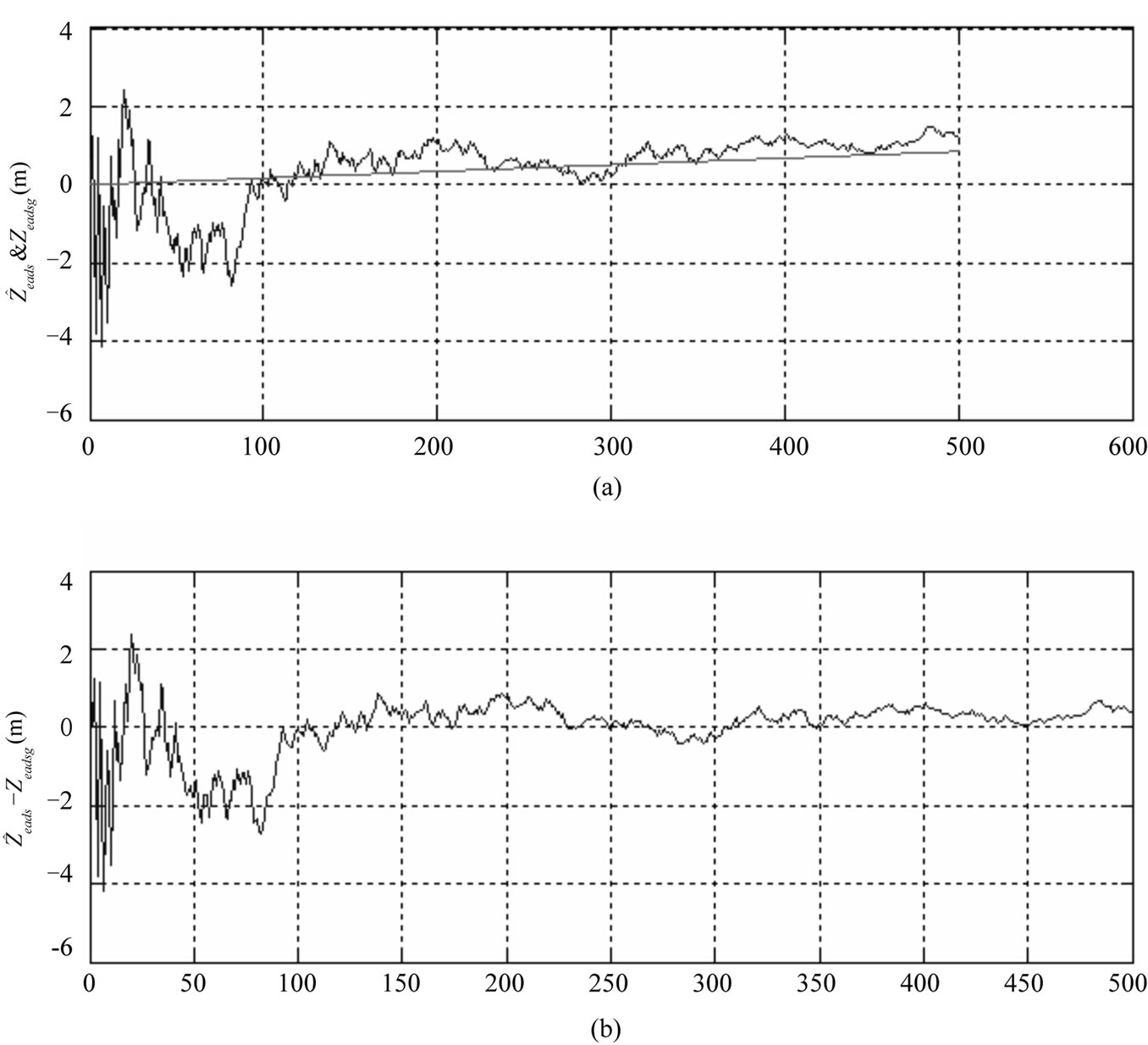
Figure 7. Z position error estimate(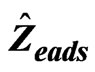 ) and actual error(
) and actual error(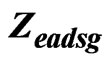 )(a) and differences between them(b).
)(a) and differences between them(b).
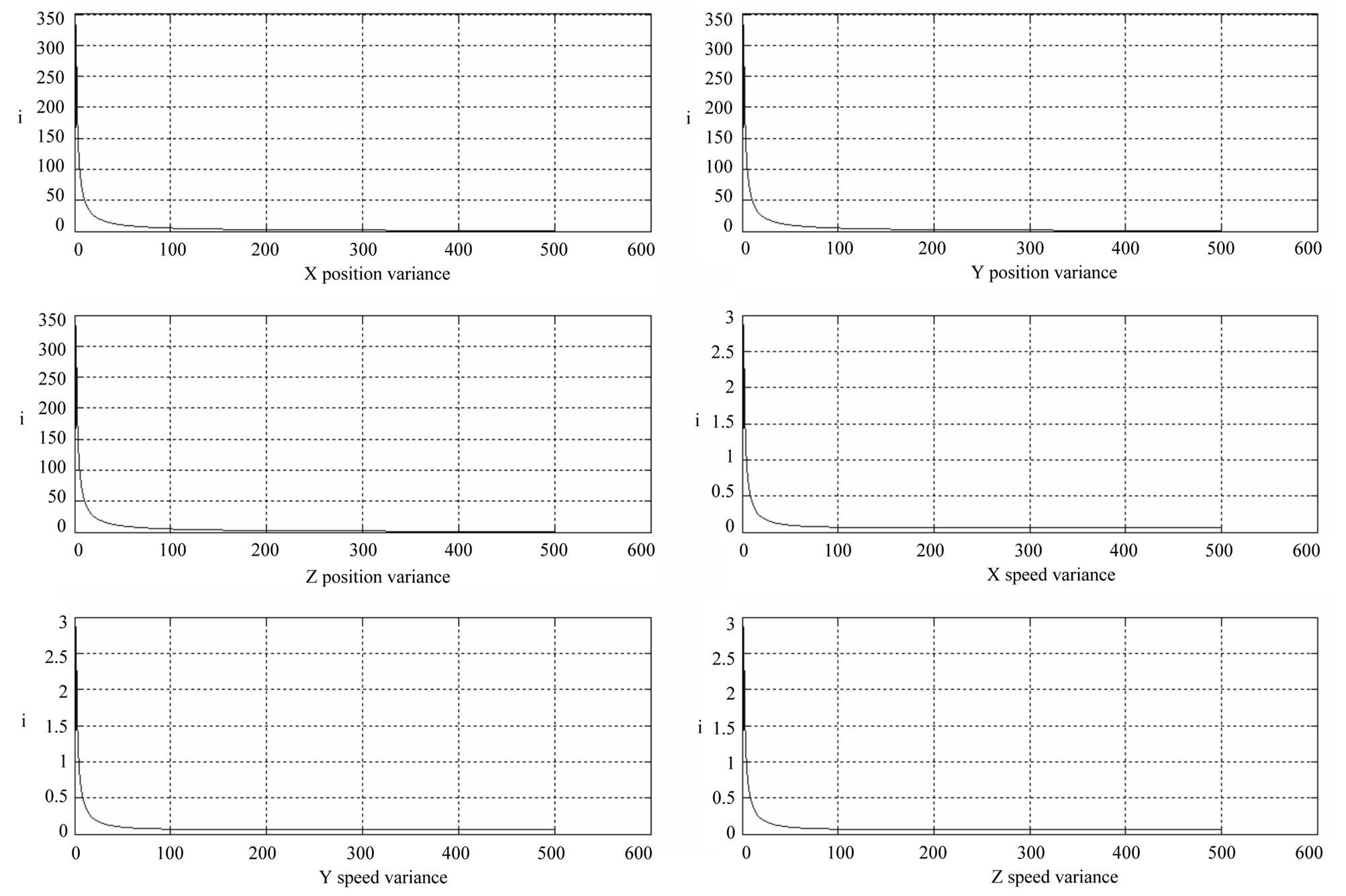
Figure 8. Position and speed error variances.
4. Conclusion
In this study two navigation systems; Air Data System and Global Positioning System has been integrated in the base of the Kalman Filter. Air Data System has high sampling frequency but poor accuracy, on the other hand GPS has low sampling frequency and higher accuracy compared to ADS. GPS can not be relied alone since it depends on satellites. ADS can be relied on since it is a stand alone system, however ADS is a Dead-Reckoning method based navigation system which has increasing errors. By integration of these two systems an integrated navigation system with high sampling frequency and high accuracy has been established. This integration provides the air speed error of the ADS which is caused by the wind speed. By finding this error, high accuracy wind speed is obtained.
5. References
[1] R. M. Rogers, “Applied Mathematics in Integrated Nnavigation Systems,” American Institute of Aeronautics and Astronautics, 2000.
[2] W. Zuo and F. Song, “Autonomous Navigation Scheme for Small Satellites GPS/Geomagnetics Integration,” Mechanical Engineering Institute, Part G: Aerospace Engineering journal Vol. 214, No. 4, 2000, pp. 207-215.
[3] Zh. Feizhou, , et al. “Application of GPS/INU/DM Integrated Position and Navigation Technologies in Smart Systems,” Beijing Hangkong Hangtian Daxue Xuebao/Journal of Beijing University of Aeronautics and Astronautics, Vol. 26, No. 3, 2000, pp. 299-302.
[4] R. Zaibel, et al., “Conference on Lasers and Electro-Optics Europe—Technical Digest 2000,” IEEE Pitscataway, NJ, USA, 00TH8505. p. 66.
[5] D. Brinkman, “Jane’s Avionics,” Jane’s Information Group. UK, 1999.
[6] R. P. G. Collinson , “Introduction to Avionics,”London : Chapman & Hall, 1996.
[7] Grişin, P. Yu., Kazarinov and M.Yu, “Fault Tolerant Dynamical Systems,” Radio i svyaz, Moskow,Russian , 1985.
[8] M. Kayton and W. R. Fried, “Avionics and Navigation Systems,” John Wiley & Sons Ltd., New York, 1997. doi:10.1002/9780470172704
[9] D. McLean, “Automatic Flight Control Systems,” Prentice Hall Inc. Englewood Cliffs, N. J. , 1990.
[10] Ch. Hajiyev, “Radio Navigation, ” Istanbul : ITU, 1999.

