Journal of Geographic Information System
Vol.6 No.3(2014), Article
ID:46914,16
pages
DOI:10.4236/jgis.2014.63021
Modeling Agricultural Change through Logistic Regression and Cellular Automata: A Case Study on Shifting Cultivation
Santiago López
School of Interdisciplinary Arts and Sciences, University of Washington Bothell, Bothell, USA
Email: cslopez@uw.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 May 2014; revised 25 May 2014; accepted 5 June 2014
ABSTRACT
Agricultural expansion is one of the prime driving forces of global land cover change. Despite the increasing attention to the factors that cause it, the patterns and processes associated with indigenous cultivation systems are not well understood. This study analyzes agricultural change associated with subsistence-based indigenous production systems in the lower Pastaza River Basin in the Ecuadorian Amazon through a spatially explicit dynamic model. The model integrates multiple logistic regression and cellular automata to simulate agricultural expansion at a resolution consistent with small scale agriculture and deal with inherently spatial processes. Data on land use and cultivation practices were collected through remote sensing and field visits, and processed within a geographic information system framework. Results show that the probability of an area of becoming agriculture increases with population pressure, in the vicinity of existing cultivation plots, and proximity to the center of human settlements. The positive association between proximity to cultivation areas and the probability of the presence of agriculture clearly shows the spillover effect and spatial inertia carried by shifting cultivation practices. The model depicts an ideal shifting cultivation system, with a complete cropping-fallow-cropping cycle that shows how agricultural areas expand and contract across space and over time. The model produced relatively accurate spatial outputs, as shown by the results of a spatial comparison between the simulated landscapes and the actual one. The study helped understand local landscape dynamics associated with shifting cultivation systems and their implications for land management.
Keywords:Logistic, Cellular Automata, GIS, Shifting Cultivation, Land Cover, Amazon

1. Introduction
Land use and land cover changes (LUCC) are the prime driving forces of transformations in the Earth system [1] . The focus of LUCC studies is generally on the identification of cause-effect relationships to uncover patterns of land uses and land covers and the processes of their change [2] . LUCC studies that concentrate on cause-effect relationships usually point at economic drivers [3] [4] , population dynamics [5] [6] , suburban sprawl factors [7] [8] , household developmental cycles [9] -[11] , transportation infrastructure [12] -[14] , tenure security [15] [16] , environmental conditions [17] [18] , and patterns of commercial agriculture and subsistence swidden land use [14] [19] [20] as major forces impacting the landscape.
Until a couple of decades ago, computational capacity constrained the operation of spatially explicit techniques to characterize human-environment interactions [21] . Advances in spatially oriented techniques that integrate spatially explicit data, as derived from remote sensors and geographic information analysis, provide new opportunities to truly incorporate innovative approaches to address fundamental questions about the relationships between social and ecological systems [22] [23] . These relatively new approaches allow researchers to identify key environmental and social variables that shape the landscape, and also to dynamically (as opposed to statically) model inherently spatial complex processes. Spatially explicit land use change models are not only capable of estimating the quantity of change and where these changes will occur over relatively long periods of time, but also useful to unravel multifaceted pattern-process relationships at different spatial and temporal scales. This study follows such an approach to analyze LUCC associated with agricultural expansion and subsistence-based production systems in tropical environments.
Spatially explicit approaches, such as cellular models, have been successful in analyzing complex spatial phenomena given their relative simplicity and flexibility. In cellular automata (CA), for instance, each cell in a spatial array exists in one of a finite set of states (e.g. a type of land cover or land use), and future states (e.g. the transition from one type of land use/land cover to another) depend on transition rules based on a local spatio-temporal neighborhood. A CA system is homogenous in the sense that the set of possible states is the same for each cell and the same transition rules apply to each cell. Time advances in discrete steps, and updates in the state of each cell may be synchronous (i.e. cells are all updated to their new state simultaneously) or asynchronous (i.e. cells are updated to their new state at different times) [24] . LUCC studies have used CA models to study frontier settlement dynamics [25] , fire spreading [26] , forest dynamics [27] , and urban growth [28] [29] [30] [31] . Most of these studies assume that the probability of change from one state to another at a time step n + 1 depends on two conditions: 1) the current state at time n and not on the sequence of states that preceded it, and 2) the transition potential of cells is determined by the influence that the spatio-temporal neighborhood exerts on a particular location. These two conditions make CA a robust framework to capture the intrinsic spatial and dynamic nature of evolving human-environment interactions.
In the past couple of decades, statistical methods such a multiple logistic regression (MLR) have been increasingly used in land cover transformation studies to analyze forest dynamics and fire dispersal [32] , agricultural and land use change [20] [33] [34] , and deforestation [12] [13] [35] . Generally, this kind of statistical studies are based on empirically parameterized static models that compute land cover change probabilities, indicating the likelihood of occurrence of a specific land use at a specific location [36] . MLR identifies the explanatory power of factors on the probability of the presence or absence of a phenomenon (e.g. agriculture), which is generally defined as a categorical variable [37] . If the observations used to generate the MLR model are spatially explicit (i.e. geolocated), the technique yields coefficients that can be used to generate maps depicting the probability of a particular location to change to a certain state or remain un-changed.
The integration of techniques such as MLR and CA, within a geographic information system (GIS) framework, is an efficient option to dynamically and spatially model LUCC. This type of synergism is suited for developing LUCC scenarios, which are themselves models of how a spatial system functions and, like other types of models, they allow explorations of understanding. At fine spatial resolutions, this type of integration allows quantifying and predicting land cover changes associated with local level spatial processes [43] . MLR/CA models of LUCC, for instance, have been successfully applied to model urban growth [38] , land changes in colonization frontiers [39] , and land use allocation in rural areas [40] -[42] . Despite the increasing popularity of MLR/CA models to study landscape dynamics, there has been only very limited research on the patterns and processes associated with subsistence based cultivation systems using this approach. Thus, this study tries to fill this gap in research and addresses the following research question: What are the patterns and processes associated with agricultural expansion in subsistence-based cultivation systems in the lower Pastaza River Basin in the Ecuadorian Amazon (PRBEA)? The emphasis is on the analytical model, presented here as an efficient alternative to simulate local landscape scenarios at fine resolutions and to illustrate its application and interpretation.
2. Study Area
This study focuses on the lower PRBEA region in Western Amazonia, which is predominantly occupied by indigenous populations. The modeling framework is applied to the case of the lowland Jívaros (the Achuar) and the Jívaro-Kichwa (the Shiwiar). Their territories encompass approximately a combined area of 930,000 ha (Figure 1) with an average population density of 0.7 persons per km2. The annual population growth rate is approximately 3.6 percent [44] . Agricultural production is limited to an area of less than 5% of the total territory and is mostly oriented towards subsistence purposes. The rate of agricultural expansion in the PRBEA is approximately 0.2 percent per annum (Figure 2, Table 1). Patterns of land use and land cover are consistent with traditional resource management practices. Indigenous families congregate around airstrips to form small semi-permanent villages. Landing strips are the only type of accessibility infrastructure in the area and constitute the centers of the communities where most families reside. Residential areas are followed by cultivation, foraging, and hunting zones [45] . The lower PRBEA is a mega bio diverse region and is currently located in the center of a variety of conservation and development projects given the region’s rich natural and cultural resources.

Figure 1. Study area—The Pastaza River Basin in the Ecuadorian Amazon.
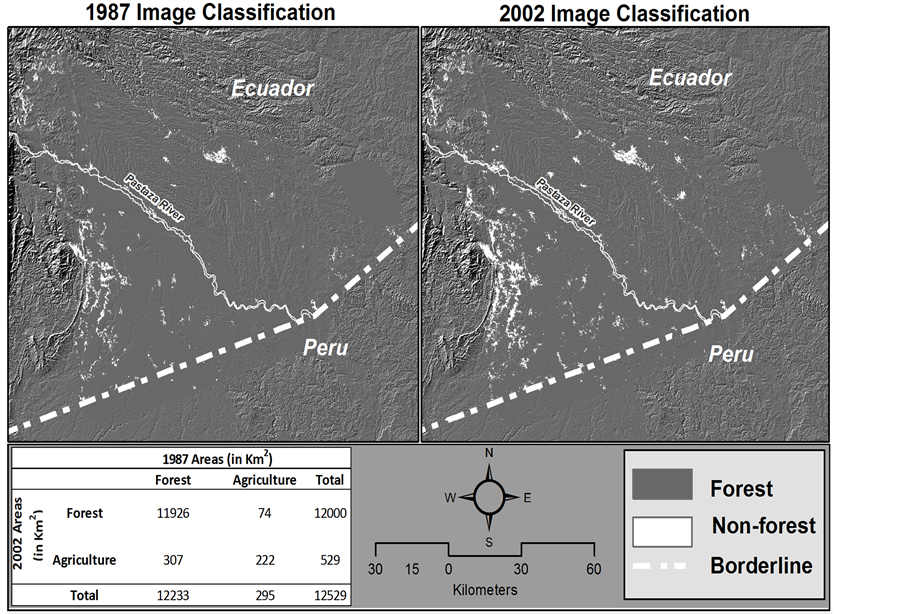
Figure 2. Post-classification comparison of agricultural and forested areas between years 1987 and 2002.
Table 1. Change detection matrix between years 1987 and 2002. Land cover changes are reported in km2 and percentages.
a: year 1987; b: year 2002; Annual conversion rate from forest to agriculture = 0.2%.
3. Methods and Materials
3.1. Data Collection and Processing
To characterize current spatial conditions in the area, a series of RGB images with a spatial resolution of < 1 m and video graphy were collected in year 2006 with the aid of an aircraft, a GPS enabled digital camera, and a video mapping system (VMS 2.0). These data were processed using digital remote sensing techniques such as image geometric correction, mosaicking, interpretation, and on-screen digitizing. With these data, a land use/land cover geo data base of 101 production units was generated that comprised residential, agricultural, and foraging areas of seven communities in the region (Figure 1). From this set, 66 were surveyed in the field to obtain not only socio-economic and demographic attributes, but also information about the structural characteristics of the production system (e.g. fallow periods, land allocation practices, production strategies). These data were processed within a GIS framework (ArcGIS v. 9.3), linking household surveyed and land use and land cover information. The vector data were transformed to raster grids and resampled to a spatial resolution of 20 m (i.e. a fourth of the minimum agricultural plot in the surveyed communities) to characterize the cultivation system. Official maps at scales of 1:25000 and 1:50000 from the Ecuadorian Military Geographic Institute were used to help describe spatial conditions (i.e. hydrography and the presence of infrastructure) in the area. Topographic conditions were derived from ASTER Global Digital Elevation Map (GDEM) data [46] . Transition rates from forest to agriculture for the region were obtained from classifications of Land sat TM and ETM satellite images of years 1987 and 2002 respectively. The data were analyzed through the integration of MLR and CA to explain landscape patterns due to variations in population numbers and environmental conditions.
3.2. A MLR/CA Land Use Change Modeling Framework
This study employs two main modeling techniques. First, it employs a MLR approach to model the presence (1) or absence (0) of agriculture in the region based on a stratified random sample of 2948 cells separated at least 60 m from each other (i.e. three times the cell resolution). A random sample may help minimize issues associated with spatial autocorrelation and obtain more efficient coefficients [13] . The model accounts for agricultural variability (La) that could be explained by a series of environmental and demographic factors [20] . The MLR model is formalized as:
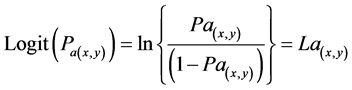 (1)
(1)
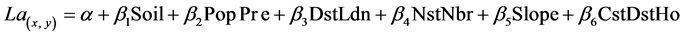 (2)
(2)
where Logit (Pa(x, y)) is the logit of the probability (Pa) of the presence of agriculture at location (x, y), α is the intercept, and βn are the slope parameters estimated via a maximum likelihood iterative procedure. The slope parameters represent how variations of the predictor affect the propensity towards agriculture. Soil is a dummy variable that depicts “good” or “bad” soil conditions and estimated from soils maps created by Ecuador’s Ministry of the Environment [47] and soil observations from the field. PopPre is the ratio between total household size and total cultivated land and estimated from household surveys and land use maps. DstLdn is the Euclidean distance from the edge of the closest landing strip to any site. NstNbr is the Euclidean distance to the nearest agricultural area. Slope is an estimate of on-site conversion costs and depicts terrain steepness or flatness and determined based on a 30 m resolution digital elevation model of the area. CstDstHo is the least accumulative cost of moving through different surfaces and terrain conditions.
Second, this study relies on a CA mechanism that simulates a decision making process, in which key and random unknown factors affect personal decisions on whether or not to expand agriculture. Some events appear to be random because agricultural expansion is a complex phenomenon and not all driving factors are known. Since all the variables are spatially explicit, the coefficients of the MLR model are used to generate a probability raster (employing Equations (1) and (2)) that is the basis for the CA model. The probability map depicts the likelihood of the presence of agriculture at every location. The CA rules determine which cells will transition from forest to agriculture based on the cell’s probability and of its eight closest neighbors. The CA algorithm was implemented in ArcGIS using Python language and is formally defined as follows:
Line 1: If 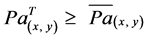 then
then 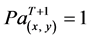 else
else 
Line 2: 
Line 3: If  then
then 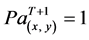 else
else 
Line 4: Go to Line 2 where Pa(x, y) is the propensity towards agriculture at location x,y at time T and estimated through MLR and extrapolated to other cells via map algebra; 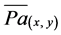 is the average probability of observed agricultural areas;
is the average probability of observed agricultural areas;
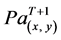 is the probability of a cell of being agriculture at location x, y at time T + 1; Nij is the average probability in a window of 3 × 3 pixels. At the beginning of the very first iteration (Line 1), the algorithm assigns a value of one (presence of agricultural area) to those cells that have a value equal or higher than the cut-off probability value (i.e. the average probability of observed cultivation areas [value = 0.6] and entered as a parameter in the model). Otherwise, the probability of the cell remains the same. If most of the area surrounding a forest patch has been transformed to agricultural use, it is likely that the patch of forest will also be cleared in the near future (based on the assumptions of the model). Line 2 takes into consideration the spatial context to update a cell’s probability based on the characteristics of the eight closest neighboring cells and its own. Line 3 compares the average probability to the cut-off probability and assigns a value of one to those cells that are equal or higher. Line 4 creates a loop in the algorithm that allows agricultural areas to expand until there are no more possible transitions utilizing the most current set of variables. The new landscape map primarily shows the presence (value = 1) or absence (values < 1) of agriculture in N years (Figure 3).
is the probability of a cell of being agriculture at location x, y at time T + 1; Nij is the average probability in a window of 3 × 3 pixels. At the beginning of the very first iteration (Line 1), the algorithm assigns a value of one (presence of agricultural area) to those cells that have a value equal or higher than the cut-off probability value (i.e. the average probability of observed cultivation areas [value = 0.6] and entered as a parameter in the model). Otherwise, the probability of the cell remains the same. If most of the area surrounding a forest patch has been transformed to agricultural use, it is likely that the patch of forest will also be cleared in the near future (based on the assumptions of the model). Line 2 takes into consideration the spatial context to update a cell’s probability based on the characteristics of the eight closest neighboring cells and its own. Line 3 compares the average probability to the cut-off probability and assigns a value of one to those cells that are equal or higher. Line 4 creates a loop in the algorithm that allows agricultural areas to expand until there are no more possible transitions utilizing the most current set of variables. The new landscape map primarily shows the presence (value = 1) or absence (values < 1) of agriculture in N years (Figure 3).
The total number of cells to change from forest to agriculture in an N-year simulation depends mostly on the cell’s probability (obtained from the probability map and modified by the influence of its spatio-temporal neighborhood) and on the transition rate from forest to agriculture for the region. Each iteration in the model represents a time step of one year since population and agricultural growth estimates are annual. The mechanism continues until there are no more possible transitions. If the extent of agriculture at a particular time step is less than the expected area, a new set of randomly chosen cells will go through the CA mechanism to determine the size and shape of agricultural areas. The system stops if the agricultural area is larger than or equal to the expected agricultural extent in N years.
Conceptually, the variables in the model can be classified as state dynamic or static. State dynamic variables are those that change over time, whereas static variables (or parameters) remain the same (Figure 4). For in-
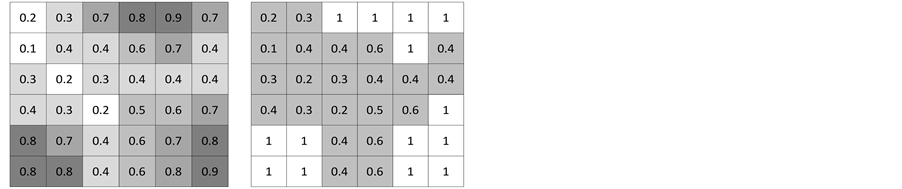 (a)
(a)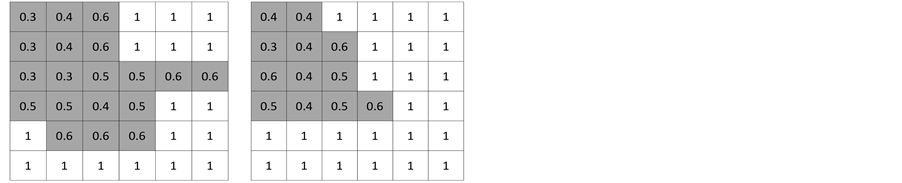 (b)
(b)
Figure 3. Probability maps before (a) and after (d) the convolution of the cellular automata engine using an average probability of 0.6. (b) and (c) show intermediate steps in the transition process.
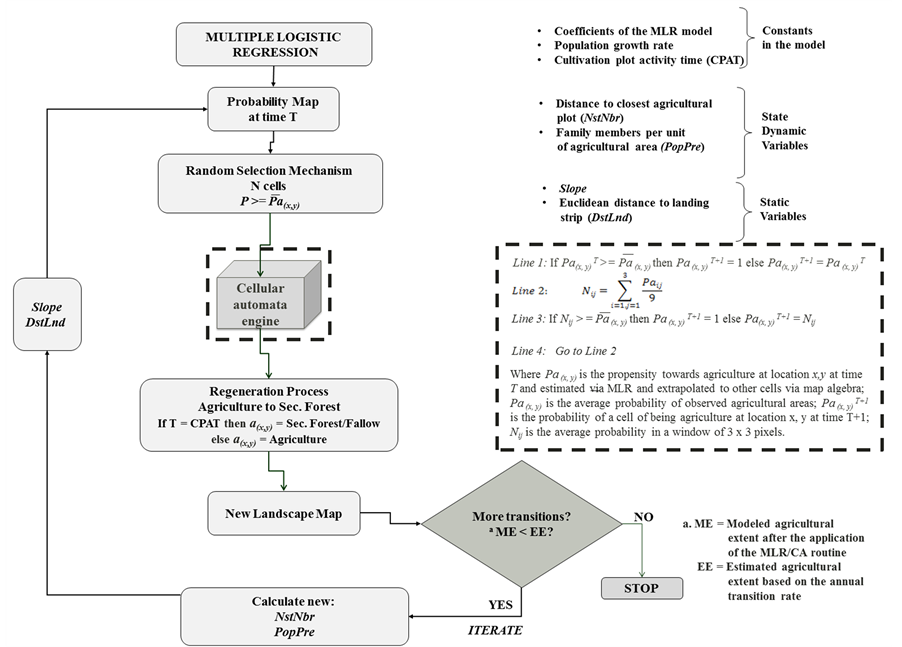
Figure 4. Conceptual logistic multipleregression/cellular automata (MLR/CA)model of shifting cultivation.
stance, distance to the closest cleared area (NstNbr) and population pressure per unit of agricultural area (PopPre) are dynamic because the actual spatial layers change during iteration. Population pressure values are updated after each iteration based on population growth estimates for the region. Slope values (Slope) and distance to land strips (DstLnd) remain the same after each time step since these are constant conditions in the long term. After each time step, a new probability map is generated using the MLR regression coefficients and the other spatially explicit variables through simple map algebra functions. If the amount of cells converted to agricultural use in a particular time period is less than the expected agricultural extent, the system iterates and new state dynamic variables are calculated. The simulation stops if the agricultural extent, after a particular iteration, is larger than or equal to the total expected agricultural area for a particular time period.
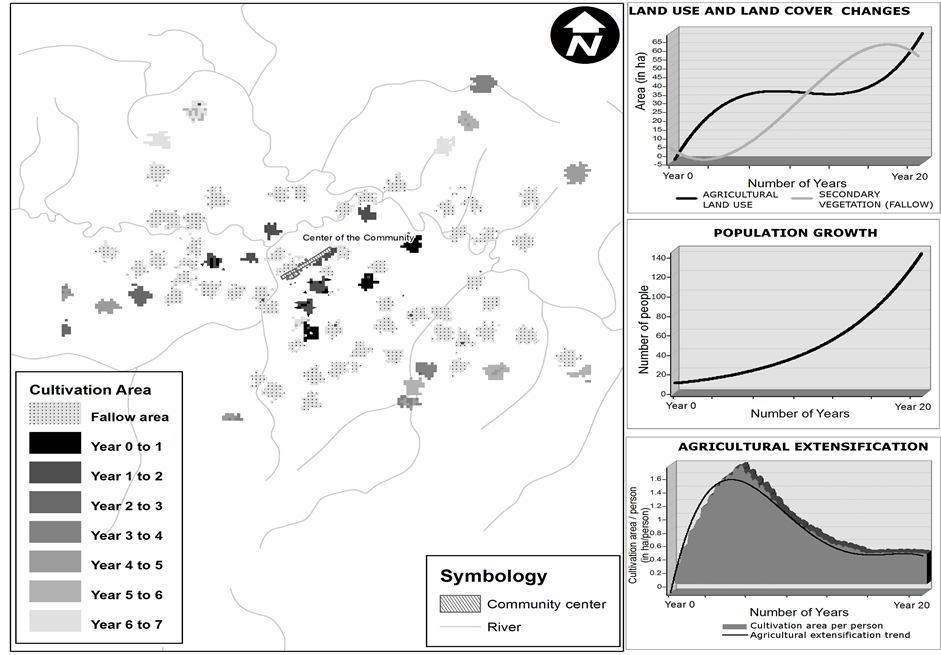
Although the transition rate from agriculture to fallow was not possible to determine because of the lack of data at a resolution consistent with household level analysis, it is still possible to determine when such transitions will occur and where. The transition from agriculture to secondary vegetation occurs after the productive cycle of an agricultural area (i.e. three years on average based for inter-fluvial communities and ten years for riverine communities). This information is entered in the model as a constant parameter. Therefore, the modeled land use maps not only show where the transitions from forest to agriculture will likely take place at a specific time step, but also the transitions from agriculture to fallow areas.
The outcomes of the MLR/CA model allow rigorous validation since it can be compared to the actual agricultural landscape. It contains no indication as to when these land cover changes might take place, but it does suggest where future changes will occur if similar recent causal processes affect the region. If conditions remain relatively stationary (as it has been the case of the populations under study), it is possible to model future land cover changes based on a series of actual known factors or to trace back landscape conditions to better understand landscape dynamics.
The simulated landscapes generated by the MLR/CA model were compared with observed data (N = 13 production units; 886 cells) of the community not included in the calibration of the statistical model. The assumption in this study is that since subsistence based communities in the PRBEA region still practice traditional shifting slash-and-burn cultivation and the methods of production and socio-economic relationships have not significantly changed in the past few decades, it is possible to characterize past landscape conditions based on the same factors that affect agricultural expansion today. This is especially the case under current land tenure regimes and social institutions that regulate the use of the land in traditional indigenous settlements.
When models are based on a neighborhood context, such as cellular automata models, parametrical statistical comparisons on a pixel-by-pixel basis are not feasible [48] . Thus, this study used a series of landscape metrics and non-parametric measures to compare our model outputs with the observed data. Examples of studies that have used similar validation approaches include [49] -[52] .
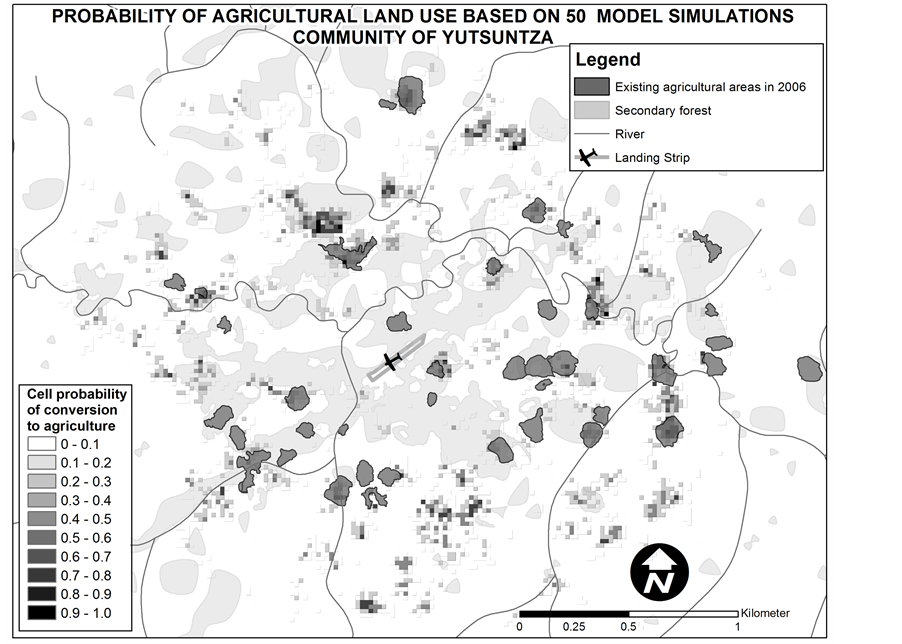
Using the MLR/CA model, 50 landscape scenarios in raster format showing agricultural (value = 1) and non-agricultural areas (value = 0) were generated and five key landscape characteristics used (i.e. total extent of agriculture, mean size of agricultural plots, distance between nearest agricultural patches, patch density, and fractal dimension) to compare the results of the model with the actual observed landscape and validate the accuracy of the predictions. These metrics were obtained using FRAGSTATS [53] .
First, comparisons were made between the averages of the five landscape metrics of the 50 simulated landscapes and the actual agricultural land use pattern of the community not used in the model’s calibration. The assessment consisted in obtaining a series of error estimates to quantify the ratios between: 1) average total extent of predicted agricultural area (Sp) and the actual extent of agricultural land use in 2006 (So), 2) mean patch area of predicted land use (MPAp) and mean patch area in 2006 (MPAo), 3) predicted mean patch density (PDp)and mean observed patch density in 2006 (PDo), 4) average nearest neighbor distance of predicted agricultural patches (NDp) and average nearest distance of agricultural plots in year 2006 (NDo), and 5) the average perimeter-area fractal dimension of the simulated landscapes (FDp) and the fractal dimension of the actual landscape in year 2006 (FDo).
Second, a Chi-square non-parametric procedure was used to examine on a cell-by-cell basis whether the difference in corresponding pixel values of both observed and predicted agricultural areas is more significant than would be expected by chance alone [54] . The null hypothesis is that there is no difference between the actual land use mosaic and the aggregated raster of agriculture/non-agriculture areas. To obtain a robust approximation of predicted agricultural areas, the simulated maps were combined into a single raster using a cell sum function in the GIS. If a cell was classified as agriculture in each of the model outcomes (value = 50), that cell had a 100% probability of conversion to agriculture. If a cell was always consistently coded as non-agriculture (value = 0), its probability of conversion to agriculture was zero. This combined raster was classified into agriculture and non-agriculture areas using the cut-off probability value (i.e. the average probability of the observed agricultural areas).
4. Results and Discussion
This study focused on the analysis of the processes and patterns associated with shifting cultivation in tropical lowlands. First, the model takes advantage of the predictive capability of MLR to compute the spatial probabilities of cells to transition from forest to agriculture based on a series of significant predictors. Results show that the probability of an area of becoming agriculture increases with population pressure (PopPre), proximity to existing cultivation plots (NstNbr), and proximity to the center of the human settlement (DstLnd), and terrain quality (Slope) (Table 2). For a more detailed discussion of the interpretation and implications of these findings please refer to [20].
Second, the MLR coefficients were used as initial slope estimates to obtain rasters in a cell-based GIS representing the conversion probability of a forest cell into agriculture. Since the spatial probabilities are highly autocorrelated (Figure 5), the model incorporates a CA mechanism to simulate the spatial spillover effect of agricultural land use and investigate the underlying spatial processes that lead to current landscape patterns. The conversion of a cell from forest to agriculture depends on the cell’s and its eight closest neighbors’ transition potential. The positive association between proximity to cultivation areas and the probability of the presence of agriculture clearly shows the spillover effect and spatial inertia carried by shifting cultivation practices; changes from one state to another are more likely to take place near areas where those changes have already occurred. Openings in the forest cover improve accessibility into forest lands and, consequently, the probability of the presence of agricultural land use increases. Cultivation areas expand and contract in the form of patches and the expansion is radial from the center of the community.
Each simulation started with the conversion from forest to agriculture at two locations representing the settlement of two families with 7 members each (i.e. the average household size of the sample) around the center of the community. This is typically the manner in which new family clusters and villages originate in the region. These locations are selected depending on initial spatial conditions (i.e. topography and distance to landing strips).Results show that at the beginning of the iterative process, forest dominates the landscape, the extent of agricultural land use is enough to support the current population, and there is no secondary vegetation (Figure 6). It is expected that agricultural areas expand at first since landholders practice extensive or labor-efficient agriculture to sustain the initial requirements of the household. As production pressure increases to supply the demand for food, agriculture is expanded throughout the communal area. When this occurs, secondary vegetation is minimal since all agricultural areas are active and under production. The simulation shows that agricultural area increases until food demand can no longer be met with this option, then extensification stops. Henceforth, agriculture is intensified in land already under cultivation as shown by the agricultural extensification graphs on both Figure 6 and Figure 7. As expansion rates decrease, the extent of land under cultivation in lands of varying quality follows a sequence opposite to expansion. Lands of low quality are taken out of production and left as fallows prior to lands of optimal quality because they require greater inputs to produce comparable yields. Hence, the extent of secondary vegetation increases. As demand increases because of population growth additional land is put into production. Lands that have been recuperated by means of fallow will be preferred to old-growth forest areas if they produce comparable yields. Areas closer to access infrastructure (i.e. landing strips) will be preferred than areas farther away since clearing this areas may be easier than old-growth forest due to lower conversion costs (e.g. lack of large trees and topographic conditions). Thus, at the end of the cycle (e.g. a 20-year process, which is age of the community that was not used in the calibration of the MLR model) the extent of secondary forest decreases and cultivation areas will again expand outwards from the center of the community ( Figure 7). In the model, the extents of cultivation and secondary vegetation depend on the cropping and fallow periods, which are obtained from field surveys and introduced in the model as input parameters. At the end, the model depicts an ideal shifting cultivation system, with a complete cropping/fallow/cropping cycle that shows how agricultural areas expand and contract across space and over time. Fifty simulated agricultural scenarios were created, quantitatively characterized, and compared with the actual landscape structure of the community not included in the calibration of the statistical model. The result of each Table 2. Results of the MLR procedure and test of significance. Source: [20] . Cox & Snell R Square: 0.40; Nagelkerke R Square: 0.88; a: Correlation is significant at a 0.001 level; b: Correlation is significant at a 0.05 level; c: Correlation is significant at a 0.1 level; d: Categorical variable: differential effect of n-1 levels of the variable. Figure 5. Semivariogram of probability values showing a strong spatial dependence at different scales. simulation is a spatial layer representing an anthropogenic landscape showing agricultural and non-agricultural areas in a 20-year period (i.e. the age of the community). The analysis of the structural characteristics of the simulated landscapes show that, the total extent of agriculture, as predicted by the model, is about 33 haon average, with agricultural plots of 0.82 ha, and a density of 3.66 patches per km2 (Table 3). The results of the comparison (Table 4) indicate that the model predicted, on average, slightly less cultivated area (0.94 < 1) than the amount obtained from the interpretation of aerial images. Cultivation plots were generally smaller than the observed average size (0.74 < 1), more regular (0.89 < 1), and their density significantly higher than the observed density (1.79 > 1). The model also predicted a more clustered arrangement of patches in comparison to the observed landscape (0.82 < 1). The differences in size of cultivation areas, patch area, and patch density are likely effects of the CA procedure. These estimates can be improved by relaxing the set of rules or by changing the cut-off probability value that determines the transition from “forest” to “agriculture”. In addition, sliver areas that are not necessarily agricultural plots, but artifacts of the CA mechanism, should not be considered in the final evaluation. The application of a filtering technique, such as a modal algorithm at the end of the iterative process, could help minimize these effects, reduce the amount of patches, and provide a better estimate of the extent of agriculture. To quantify the spatial correlations between the simulated landscapes and the observed one, the 50 simulated land use layers were combined into one layer that depicts the conversion certainty of each cell (Figure 8). The Figure 6. Results of a simulation after one year. Agricultural extensification increases (bottom-right corner graph) as the demand for food increases due to steadily population growth. Table 3. Descriptive statistics of five landscape metrics use to evaluate the performance of the MLR/CA model. N = 50. Table 4. Results of the analysis of the structural characteristics of the simulated landscapes. Descriptive statistics and mean errors of the ratios between observed and predicted landscape metrics. a: Ratios between average predicted values of 50 MLR-CA model outcomes and observed values of the community not used in the MLR model estimation. Figure 7. Results of a simulation after 20 years. The simulation shows an expansive behavior of agricultural land use at initial phases of village formation. As population grows there is a transition from extensive to intensive practices. Intensification may occur by producing higher yields per unit of area or by shortening fallow periods. results of the Chi-square procedure show that a significant statistical relationship exists between both the observed and predicted distributions at significance level of 0.05, however this relationship is weak (Cramer’s Phi Statistic = 0.03) (Table 5). Thus, the non-parametric evaluation shows that the model predicted the location of cultivation areas reasonably well. However, since the surface depicting the accumulated simulations shows all possible locations and only a fraction of these actually match the observed cultivation areas, the strength of the correlation is low. 5. Conclusions This study focused on the analysis of agricultural expansion in subsistence based production systems through the implementation of a MLR/CA model. The MLR procedure showed that population pressure is the most important predictor of the presence of agriculture in the region; larger families demand more land resources for food production. At a local level, the effect of population pressure on land cover is intertwined with other factors such topographic conditions and the spatial structure of the land use system. This finding is consistent with other studies in indigenous areas that show similar associations between LUCC, demographics, and ecological factors [55] -[57] . Since landscape change is an inherently spatial and dynamic phenomenon, the identification of factors associated with the presence of agriculture is only the first step in the attempt to understand the processes associated with land cover change. Based on the identification of key variables that explain the presence of agriculture, this study applied a modeling framework in which time and space are explicitly incorporated into one system. However, this was not a simple task; the lack of multi-temporal spatial data with the appropriate level of detail hindered the development of a land cover change model based on spatial trajectories because these approaches rely on spatial information of past periods to extrapolate future changes. As an alternative, this study suggested a Figure 8. Predicted cultivation areas based on the aggregation of 50 land use simulations and observed cultivation areas of the community not used in the calibration of the MLR model. Table 5. Results of the chi-square procedure evaluating the statistical relationship between predicted and observed agricultural land use areas. a: Predicted by the model; b: Observed; Chi Square = 22.973; Probability (p) = 0.0001; Critical Chi Square = 3.8414; Degrees of freedom = 1; Cramer's Phi Statistic = 0.03. combination of MLR and CA to simulate agricultural expansion scenarios based on the assumption that future changes will depend on the most current processes of agricultural expansion and not on previous ones. The approach concurrently synthesizes demographic, environmental, and spatial factors to adequately quantify agricultural expansion in subsistence production areas. The MLR/CA model implemented in this study is flexible for experimentation and further insights can be obtained on how changes in the social and spatial configuration of local populations may affect landscape composition. Ultimately, the model has the ability to generate spatially explicit projections that allow improving our understanding of the interaction between the demand for land resources and the intrinsic dynamics of land cover change associated with subsistence-based shifting cultivation systems. The spatial model presented here produced accurate results, especially in regards to the extent of cultivation, and the size and shape of cultivation areas. However, some other structural landscape characteristics (density and clustering of the agricultural mosaic) were less accurately estimated. The model also presents some limitations because it is constrained by: 1) global and deterministic transition rules (applied to all cells and known), which results in the “homogenization” of human behavior; people made the same decisions about landscape utilization based on similar known pre-conditions, which hindered the representation of individual preferences, 2) constant demographic and agricultural expansion growth rates that may not reflect conditions of individual households at a particular time step, and 3) the assumption of long term linear relationships among driving factors of LUCC. The ability of the model to add randomness into the simulation process helped to deal with the first limitation. In this particular study, the introduction of randomness during the selection of cells accounts for the lack of complete data on human behavior (e.g. values, experience, ability) affecting decisions on land allocation, accounts for modeling the average case and not the individuals, and gives some kind of assignation to human preferences. The second and third limitations restrict the application of the model to conditions of steadily population growth and known relationships between land-cover change factors. Although these issues may be problematic in the long term, in the short term the model may help estimate agriculture expansion with good results, as shown with the comparison procedure of the 50 spatial simulations. In general, there are two main aspects of this research that should be highlighted. First, if populations in the region continue to grow as some studies have suggested [58] [59] , then the area of agricultural land will increase until intensification occurs. This study suggests that agriculture intensification through improved management techniques (e.g. improved weed control, biological fertilization, agro-forestry) could be a strategy to reduce human pressure on tropical forests and help preserve their resources. Unplanned radial agricultural extensification, a process that characterizes the spatial dynamics of land cover change in indigenous territories in the Amazon basin and that was clearly depicted in this study, may reduce forest extent and forest resources in the long term and may not be desired. Second, the model could assist the development of a support system for land management policy that wishes to capture the complexity of indigenous resource use strategies. Landscape scenarios, like the ones discussed in this study, could be integrated into comprehensive management plans and help fill gaps of information, especially in situations where socio-economic, demographic, and spatial data are scarce (like those of several indigenous territories in the Amazon basin). Acknowledgements This research at different stages was supported by the Tinker Foundation, the College of Liberal Arts of the University of Texas at Austin, the National Science Foundation, and the Gordon and Betty Moore Foundation. In Ecuador, our special thanks to Nacionalidad Achuar del Ecuador (NAE) and Nacionalidad Shiwiar del Ecuador (NASHIE) for allowing this research and providing the institutional support. Julian Ilianes, Eddie Villamil, Santiago Ayuy, and Clemente Tiriats provided invaluable assistance during field work activities. Rodrigo Sierra, David Stokes, Jin-Kyu Jung, and three anonymous reviewers provided insightful comments on previous versions of this document. References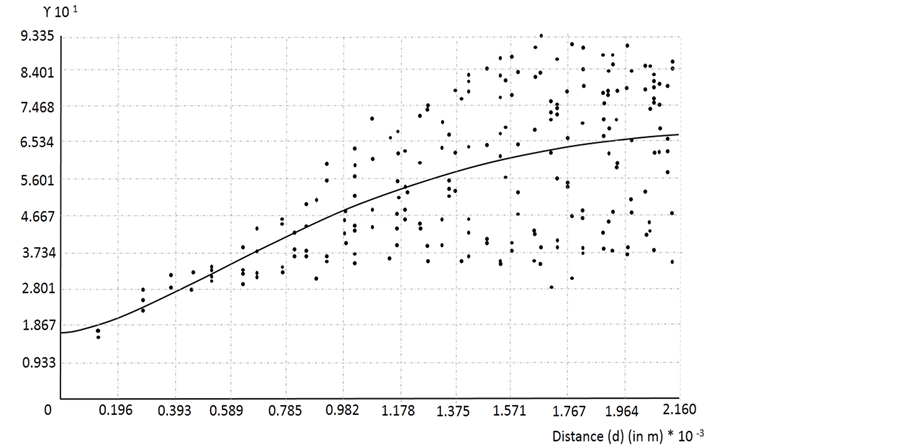

http://dx.doi.org/10.1038/ngeo756
http://dx.doi.org/10.1007/s10745-007-9141-6
http://dx.doi.org/10.1007/BF00131257
http://dx.doi.org/10.1016/j.worlddev.2006.02.009
http://dx.doi.org/10.1111/0004-5608.00205
http://dx.doi.org/10.2307/3147089
http://dx.doi.org/10.1023/A:1024430026953
http://dx.doi.org/10.1023/A:1011901023485
http://dx.doi.org/10.1016/j.ecolmodel.2006.12.039
http://dx.doi.org/10.1016/j.compenvurbsys.2008.06.006
http://dx.doi.org/10.1016/S0167-8809(01)00188-8
http://dx.doi.org/10.1080/13658811003752332
http://dx.doi.org/10.1016/S0301-4797(05)80038-6
http://dx.doi.org/10.1080/13658810210157769
http://dx.doi.org/10.1016/j.jag.2010.09.008
http://www.umass.edu/landeco/research/fragstats/fragstats.html
http://dx.doi.org/10.1111/j.1523-1739.2005.00194.x
http://dx.doi.org/10.1353/lar.2005.0012.


