Natural Science
Vol.08 No.04(2016), Article ID:66027,15 pages
10.4236/ns.2016.84023
Approximate Analytical Expressions for the Concentrations of Acetate and Methane in the Microbial Electrochemical Cell
Sivasamy Pavithra1, Lakshmanan Rajendran1*, Raghavan Ashokan2
1Department of Mathematics, Sethu Institute of Technology, Kariapatti, India
2Department of Mathematics, Madurai Kamaraj University, Madurai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
Mathematical modeling of microbial electrochemical cells (MXCs) for both microbial fuel cell and microbial electrolysis cell is discussed. The model is based on the system of reaction diffusion of reaction-diffusion equation containing a non-linear term related to substrate consumption rates by electrogeneic and methanogenic microorganism in the bioflim. This paper presents the approximate analytical method to solve the non-linear differential equation that describes the diffusion coupled with acetate (substrate) consumption rates. Simple analytical expressions for the concentrations of acetate and methane have been derived for all experimental values of bulk concentration, distributions of microbial volume fraction, local potential in the biofilm and biofilm thickness. In addition, sensitivity of the parameters on concentrations is also discussed. Our analytical results are also validated with the numerical results and limiting cases results. Further, a graphical procedure for estimating the kinetic parameters is also suggested.
Keywords:
Mathematical Modeling, Microbial Fuel and Electrolysis Cells, Waste Water Treatment, Boundary Value Problems, Non Linear Equations

1. Introduction
Microbial fuel cells (MFC) can be defined as a microbial catalyzed electrochemical system which can facilitate the direct conversion of substrate to electricity through a cascade of redox reactions, especially in the absence of oxygen [1] . The applications of MFC are widespread in different fields including waste water remediation, toxic pollutants/xenobiotics removal, recovery of commercially viable products, sequestration of CO2 harvesting the energy stored in marine sediments, desalination, etc. [1] . Microbial electrochemical cells are recognized as a modern technology to directly utilize bioenergy stored in organic substances, especially in wastewater [2] . Several experiments have been conducted to evaluate MXCs main performance as a current or hydrogen generator fed with different organic matters [3] and [4] . A simple mediator based model with suspended cells was investigated [5] . A simple model with rapid implementation and computations is used to describe the effect of some operational conditions such as temperature and substrate concentration on in the MFC performance [6] . Pinto developed a time-dependent mathematical model with the uniform distribution of bacteria in the anode chamber. Although a number of MFC mathematical models have been developed and discussed. To the best of the knowledge, only one MEC model has been proposed [7] . Yahya modified this model for a fed-batch reactor. It is a multi population mediator-based model developed based on the Bernard’s anaerobic digestion kinetics model [8] . Alavijeh [2] used a variety of approaches to develop the first generalized conduction-based model for MXCs including both MFCs and MECs. It is a one-dimensional spatial distribution and time-dependent model using Bernard’s anaerobic digestion kinetics model and both biofilm and liquid bulk simulation. The purpose of this communication is to derive the analytical expression for acetate and methane concentration using the Adomain decomposition method. We also provide the tabular complication of concentration of acetate with limiting case results (first order and zero order kinetics).
2. Mathematical Formulation of the Problem
Anolyte contains fermentative microorganisms and acetoclastic methanogens. Biofilm contains acetoclastic methanogens and anode respiring bacteria (electrogens). Acetate is produced during fermentation process and then diffuses to the biofilm where electrogens consume it and conduct electrons to the anode surface [2] . The systematic diagram of the model is represented in Figure 1.
The acetate and methane mass transfer equations through the biofilm are described as follows [2] :
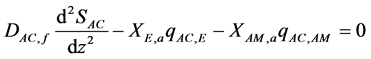 (1)
(1)
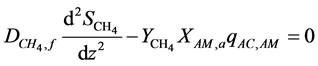 (2)
(2)
Figure 1. Schematic representation of the model [1] .
where 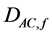 and
and 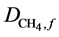 the diffusion coefficient of acetate and methane in the bioflim
the diffusion coefficient of acetate and methane in the bioflim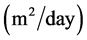 .
. 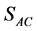 and
and 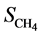 are the concentration of acetate on the biofilm
are the concentration of acetate on the biofilm 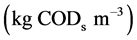 and methane concentration on the biofilm
and methane concentration on the biofilm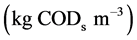 .
.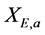 ,
, 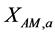 and
and 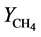 are the density of biomass
are the density of biomass 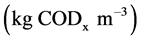 yield coefficient. The acetate consumption rate by electromagnetic microorganism in the biofuel
yield coefficient. The acetate consumption rate by electromagnetic microorganism in the biofuel 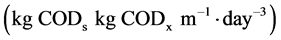 is represented by the Nenst-Monoid equation [2]
is represented by the Nenst-Monoid equation [2]

where 






where 






where 








Using the above dimensionless variables the non-linear reaction-diffusion Equations ((1) and (2)) are expressed in the following dimensionless form:


The boundary conditions can be written as follows:




3. Approximate Analytical Expression of Concentration of Acetate and Methane
Recently, many authors have been applied the Adomain decomposition method (ADM) to various problems and demonstrated the efficiency of the ADM for handling non-linear problem in physics and engineering sciences [9] - [13] . The modified Adomain decomposition method [11] is used to give the approximate solutions of the non-linear Equations ((7) and (8)). Many researchers find that the ADM requires less computational work than traditional approaches [11] - [13] . Other advantages include the ability to solve nonlinear problems without linearization, the wide applicability to several types of problems and scientific fields, and the development of a reliable, analytic solution. Many researchers find that the ADM requires less computational work than traditional approaches [11] - [13] . Other advantages include the ability to solve nonlinear problems without linearization, the wide applicability to several types of problems and scientific fields, and the development of a reliable, analytic solution. Using this method (refer Appendix A), we can obtain the concentrations acetate and methane as follows:


where the constants

Equations ((13) and (14)) are valid provided 

4. Limiting Case
4.1. Unsaturated (First Order) Catalysis
We initially consider the situation where the concentration of acetate 






Hence, the non-linear Equations ((7) and (8)) have been reduces to linear equations. Now, the concentration of acetate 



where 

4.2. Saturated (Zero-Order) Catalysis
We now consider that the second major limiting situation found in practice, when the concentration of acetate and methane is very much greater than the half saturation constants 




The above Equations ((17) and (18)) are linear reaction-diffusion equations which are exactly solvable. By solving the above Equations ((17) and (18)), we can obtain the concentration of Acetate (16), and Methane (17).


Equations ((22) and (23)) are the exact solution of Equations ((20) and (21)).
4.3. Saturated Electrogenic Microorganism and Acetoclastic Methanogens Are Equal (α = β)
In this case, Equations ((7) and (8)) become as follows:


In this case, the above non-linear equation can be solved using Adomain decomposition method. Now, the concentrations become


where the constants 


5. Discussion
Equations ((7) and (8)) represent the general closed-form of analytical expression for the concentrations of acetate and methane for non steady state condition and for various system parameters (potential, saturation parameter of electrogenic microorganism and acetoelastic methanogenes, the diffusion coefficient of acetate, ratio of the thickness of the biofilm and boundary layer). It is of interest to compare the influence of each parameter on the concentration of acetate and methane for various realistic experimental parameters.
Influence of Potential on the Concentration of Acetate. The influence of dimensionless potential on the concentration of the acetate for some experimental values of parameters is shown in Figure 2(a). The microbial activity is strongly dependent on the redox potential of the anode. From this figure it is observed that the concentration of acetate decreases when 
Influence of Saturation Parameter of Electrogenic Microorganism 

Figure 2. Plot of dimensionless concentration 





acetate increases when saturation parameter of electrogenic microrganism 

Influnce of the Ratio of Thickness of the Biofilm and the Boundary Layer. Figure 2(d) represents the concentration verses distance from the anode surface for various values of 

Influence of Other Parameters of the Concentration of Methane and Acetate. The concentration of methane versus dimensionless distance x for various experimental values of parameters is plotted in Figure 3. From these figure, it is interfered that the concentration of methane increases when 

Figure 4 represents the dimensionless concentrations of acetate versus potential for various values of 




Figure 3. Plot of dimensionless concentration of 





Figure 4. Plot of dimensionless concentration 




6. Comparison with Numerical Data and Limiting Case Results
The non-linear differential Equations ((9) and (10)) for the given initial-boundary conditions are being solved numerically. The function pdex, in Matlab software which is a function of solving the initial-boundary value problems for non-linear ordinary differential equations is used to solve this equation. Its numerical solution is compared with analytical results in Table 1. The maximum relative error between our analytical result and the numerical result is 0.32%. The Matlab program is also given in Appendix C. The concentration of acetate and methane are also obtained for the following limiting cases, that is zero order kinetics, first order kinetics and saturated electrogenic microorganism and saturated acetoclastic methanogens are equal
7. Determination of Kinetic Parameters KAC,E, qAC,AM,max, φE,a, α and β
The acetate consumption rate by electromagnetic microorganism in the microbial fuel cell (Equation (3)) can be written as follows:
Table 1. Comparison of the acetate concentration 


Figure 5. Plot of two dimensional comparative diagram of general solution of dimensionless Acetate concentration 




As shown in Figure 6, 





From Equation (10), we can obtain the concentration of acetate at bioflim and anode interface as

Now the plot of 





Figure 6. Estimation of kinetic parameters 

Table 2. Nomenclature.
8. Conclusion
A theoretical model describing the bio energy production using microbial electrochemical cell via Nernst-Mo- noid kinetics is analyzed. The time independent non-linear partial differential equations have been solved analytically using the Adomain decomposition method. The primary result of this work is the approximate analytical expression of concentration of acetate and methane for all values of parameters. The influence of potential, ratio of thickness of biofilm and boundary layer, etc. on the concentration of acetate and methane is discussed. Our results are in excellent agreement with stimulation and limiting case results. Also two graphical procedures are suggested for estimating the kinetic parameters.
Acknowledgements
This work was supported by the DST SB/SI/PC-50/2012, New Delhi, India. The authors are thankful to Mr. S. Mohamed Jaleel, The Chairman, Dr. A. Senthilkumar, The Principal, Dr. P. G. Jansi Rani, Head of the Department of Mathematics, SethuInistitute of Technology, Kariapatti-626115, Tamilnadu, India for their encouragement.
Cite this paper
Sivasamy Pavithra,Lakshmanan Rajendran,Raghavan Ashokan, (2016) Approximate Analytical Expressions for the Concentrations of Acetate and Methane in the Microbial Electrochemical Cell. Natural Science,08,196-210. doi: 10.4236/ns.2016.84023
References
- 1. Mohan, S.V., Srikanth, S., Velvizhi, G. and Lenin Babu, M. (2013) Microbial Fuel Cells Forsustainable Bioenergy Generati-On: Principles and Perspective Applications. Biofuels Technologies, 14, 335-368.
- 2. Alavijeh, M.K., Mardanpour, M.M. and Yaghmaei. S. (2015) A Generalized Model for Complex Waste Water Treatment with Simultaneous Bioenergy Production Using the Microbial Electrochemical Cell. Electrochimica Acta, 167, 84-96.
- 3. Pant, D., Van Bogaert, G., Diels, L. and Vanbroekhoven, K. (2010) A Review of the Substrates Used in Microbial Fuel Cells (MFCs) for Sustainable Energy Production. Bioresource Technology, 101, 1533-1543. http://dx.doi.org/10.1016/j.biortech.2009.10.017
- 4. Kadier, A., Simayi, Y. Kalil, M.S. Abdeshahian, P. and Hamid, A.A. (2014) Review of the Substrates Used in Microbialele-Ctrolysis Cells (MECs) for Producing Sustainable and Clean Hydrogen Gas. Renewable Energy, 71, 466-472. http://dx.doi.org/10.1016/j.renene.2014.05.052
- 5. Zhang, X.-C. and Halme, A. (1995) Modelling of a Microbial Fuel Cell Process. Biotechnology Letters, 17, 809-814. http://dx.doi.org/10.1007/BF00129009
- 6. Oliveira, V.B., Simoes, M., Melo, L.F. and Pinto, A.M.F.R. (2013) A 1D Mathematical Model for a Microbial Fuel Cell. Energy, 61, 463-471. http://dx.doi.org/10.1016/j.energy.2013.08.055
- 7. Pinto, R.P., Srinivasan, B., Manuel, M.F. and Tartakovsky, B. (2010) A Two-Population Bioelectrochemical Model of a Microbial Fuel Cell. Bioresource Technology, 101, 5256-5265. http://dx.doi.org/10.1016/j.biortech.2010.01.122
- 8. Yahya, A.M., Hussain, M.A. and Abdul Wahab, A.K. (2015) Modeling Optimization, and Control of Microbial Electrolysis Cells in a Fed-Batch Reactor for Production of Renewable Bio Hydrogen Gas. International Journal of Energy Research, 39, 557-572. http://dx.doi.org/10.1002/er.3273
- 9. Praveen, T. and Rajendran, L. (2011) Mathematical Model for Multi-Phase Micro Channel Bioreactors. International journal of Mathematical Archive, 2, 2270-2280.
- 10. Saravanakumar, K. and Rajendran, L. (2011) Analytical Solution of the Concentration of Substrate and Effectiveness Factor for Acetophenone in Packed Bed Reactor. International Journal of Mathematical Archive, 2, 2347-2357.
- 11. Yahya, Q.H. and Liu, M.Z. (2009) Solving Singular Boundary Value Problems of Higher Order Ordinary Differential Equation by Modifiedadomain Decomposition Method. Communications in Nonlinear Science and Numerical Simulation, 14, 2592-2596. http://dx.doi.org/10.1016/j.cnsns.2008.09.027
- 12. Yahya, Q.H. (2012) Modified Adomian Decomposition Method for Second Order Singular Initial Value Problems. Advances in Computational Mathematics and Its Applications, 1, 2.
- 13. Yahya, Q.H. and Liu, M.Z. (2008) Modified Adomian Decomposition Method for Singular initial Value Problems in the Second-Order Ordinary Differential Equations. Surveys in Mathematics and Its Applications, 3, 183-193.
Appendix A: Basic Concept of the Adomain Decomposition Method
This is given in the supplementary material of the manuscript.
Appendix B: Approximate Analytical Solution of Non Linear Equation (7) Using ADM
In this appendix, we indicate how Equation (6) in this paper is derived. Furthermore, an ADM is constructed to determine the solution of Equation (4) in the operator form,

where


where A and B are the constants of integration. We let,


where

From Equations ((B.3) to (B.5)), Equation (B.2) becomes

We identify the zeroth component as

and the remaining components as the recurrence relation

where 




Adding (B.9) and (B.10), we can obtain the concentration of acetate as described in Equation (10) in the text. By substituting the values of 
Appendix C: Scilab/Matlab Program for the Numerical Solution of Equation
This is given in the supplementary material of the manuscript.
Supplementary Material of the Manuscript
Appendix A: Basic Concept of the Modified Adomain Decomposition Method
Consider the singular boundary value problem of 

where N is a non-linear differential operator of order less than n, 


where

The inverse operator 


By applying 

Such that
The Adomian decomposition method introduce the solution 


and

where the components 


can be used constant Adomian polynomials, when 

Through using modified Adomian decomposition method, the components 

which gives

From (A.8) and (A.11), we can determine the components


can be used to approximate the exact solution. The approach presented above can be validated by testing it on a variety of several linear and nonlinear initial value problems.
Appendix C
Scilab/MatlabProgram for the Numerical Solution of Equation (4)
function pdex4
m = 0;
x = linspace (0, 1);
t = linspace (0, 100000);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
%――――――――――――――――――――?
Figure
plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,1)')
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c =1;
f =1.* DuDx;
e=0.3;alpha=2;
F =-(e*u(1))/((1+(alpha*u(1))));
s =F;
% ――――――――――――――――――――?
function u0 = pdex4ic(x);
u0 = [0];
% ――――――――――――――――――――?
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
j=10;
pl = [0];
ql = [1];
pr = [-j*(1-ur(1))];
qr = [1];
NOTES
*Corresponding author.










