Received 28 April 2015; accepted 6 June 2015; published 9 June 2015

ABSTRACT

This paper is devoted to studying the generalized Chaplygin gas models in Bianchi type III space- time geometry with time varying bulk viscosity, cosmological and gravitational constants. We are considering the condition on metric potential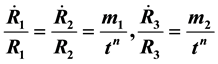. Also to obtain deterministic models we have considered physically reasonable relations like, 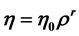and the equation of state for generalized Chaplygin gas given by. A new set of exact solutions of Einstein’s field equations has been obtained in Eckart theory, truncated theory and full causal theory. Physical behaviour of the models has been discussed.

Keywords:

Bianchi Type III, Bulk Viscosity, Cosmological Constant, Gravitational Constant, Generalized Chaplygin Gas

1. Introduction

The motivation behind the stimulated interest in anisotropic cosmological models is experimental study of isotropy of the cosmic microwave background radiation and speculation about the amount of the helium formed at the early stages of the evolution of the universe. The existence of anisotropic stage of the universe is supported by experimental data and numbers of scientific arguments in the literature which is supposed to be phased out during evolution. The present day universe is isotropic and homogeneous. In understanding the behavior of universe at early stages, anisotropic cosmological models have played a significant role. Singh and Singh [1] [2] have obtained cosmological models for Bianchi type V, VI₀, III and Kantowski-Sachs space-times within framework of Lyra geometry. Bianchi type III cosmological model in f(R, T) theory of gravity has been discussed by Reddy et al. [3] . Pradhan et al. [4] discussed anisotropic Bianchi type III string cosmological models in normal gauge for Lyra’s manifold with electromagnetic field. Singh et al. [5] have investigated Bianchi type III cosmological models in Lyra’s geometry in the presence of massive scalar field.

The astronomical observations of type Ia supernovae [6] - [10] , galaxy red shift surveys [11] , cosmic background radiation data [12] [13] and large scale structure [14] convincingly suggest that present universe is undergoing the accelerated phase of expansion. To understand this accelerated behavior of universe, cosmological constant played a significant role. A large cosmological constant at early epoch is the basis of the inflationary model and the much smaller cosmological constant at a much later epoch is suggested by current observations. In an attempt to solve the discrepancy between the cosmological constant inferred from observations and the vacuum energy density resulting from quantum field theories, many researchers have proposed cosmological models with time varying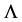. Sahni and Starobinski [15] have presented detailed discussion on current observational situation focusing on cosmological tests on.

The idea of variability of G originated with the work of Dirac [16] , who for the first time drew the attention of the scientific community to the time varying G in context of cosmological model. The theory of an expanding universe supports the idea of time-dependent gravitational constant. Time varying G has many interesting consequences in astrophysics. It is shown that G varying cosmology is consistent with whatsoever cosmological observations available at present [17] . Variability of G is also supported by observational results coming up from Lunar Laser Ranging [18] . Anisotropic cosmological models with bulk viscosity, variable G and 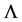have been investigated by Chakraborty and Roy [19] . Singh and Beesham [20] have discussed anisotropic Bianchi type V perfect fluid space-time with variable G and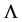. Singh [21] has focused on Robertson-Walker model with variable cosmological term and gravitational constant in cosmological relativity theory. Khurshudyan et al. [22] have studied observational constraints on models of the universe with time-variable gravitational and cosmological constants along modified gravity theory.

In the literature it has been discussed that during the early stages of evolution of the universe, bulk viscosity could arise in many circumstances and could lead to an effective mechanism of galaxy formation [23] . To consider more realistic models one must take into account the viscosity mechanism, which has already attracted the attention of many researchers. Bulk viscosity leading to an accelerated phase of the universe today has been studied by Fabris et al. [24] . Singh et al. [25] have presented a number of classes of solutions of Einstein’s field equations with variable G and 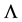and bulk viscosity coefficient in the frame work of non-causal theory. Singh and Chaubey [26] , and Singh and Baghel [27] [28] have discussed some Bianchi type models with bulk viscosity. Recently Kotambkar et al. [29] have investigated anisotropic cosmological models with quintessence considering the effect of bulk viscosity.

It has been observed that the universe has entered an acceleration phase and some exotic dark energy must presently dominate [30] [31] . This hypothetical form of energy that permeates all of space tends to increase the rate of expansion of the universe. Hence in order to explain recent cosmic observations, dark energy is considered as prime candidate. Chaplygin gas may be useful for describing dark energy because of its negative pressure. Chaplygin gas (CG) is referred as exotic fluid, as it has positive energy density but negative pressure. Due to effectiveness of CG in explaining the evolution of the universe, several generalizations of Chaplygin gas have been proposed in the literature [32] - [34] . The form of equation of state (EOS) of matter is generalized by adding an arbitrary constant with an exponent over the mass density, referred as generalized Chaplygin gas (GCG) [35] [36] . The form of EOS is modified by adding an ordinary matter field, matching the recent observational fallouts GCG referred as modified Chaplygin gas (MCG) [37] . Alcaniz et al. [38] have investigated cosmological models with high red shift objects and the generalized Chaplygin gas. Paul et al. [39] have studied observational constraints on modified Chaplygin gas.

2. Field Equation

We consider the Bianchi type III metric in the form

(1)

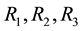are function of t alone.

For perfect fluid distribution Einstein’s field equations with gravitation and cosmological constant may be written as

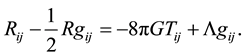(2)

where G is gravitational constant, is cosmological constant, which are time dependent.

The energy momentum tensor 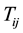for viscous fluid distribution is given by

(3)

where

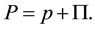(4)

where p is equilibrium pressure, is bulk viscous stress together with.

Einstein’s filed Equation (2) for the metric (1) leads to

(5)

(6)

(7)

(8)

(9)

where the over head dot denote differentiation with respect to time t. An additional equation for the time changes of G and is obtained by divergence of the Einstein tensor, i.e. which leads to, yielding

(10)

Equation (10) splits into two equations as

(11)

(12)

For the full causal non-equilibrium thermodynamics the causal evolution equation for bulk viscosity is given by [40]

(13)

absolute temperature, is bulk viscosity coefficient which cannot become negative, denote the relaxation time for transient bulk viscous effects. Causality requires. When, Equation (13) reduces to evolution equation for truncated theory. For Equation (13) reduces to evolution equation for full causal theory and for Equation (13) reduces to evolution equation for non-causal theory (Eckart’s theory).

3. Cosmological Solutions

Since there are five basic Equations (5)-(9) and eight unknowns viz. therefore three more physically plausible relations among these variables will be considered for solving the set of equations.

Case I: Non-Causal Cosmological Solution

For non causal solution , therefore the evolution Equation (13) takes the form of

(14)

To find the complete solution of the system of equations, following relations are taken into consideration.

The power law relation for bulk viscosity is taken as

(15)

and r is constant.

The equation of state is

(16)

We assume the solution of the system in the form

(17)

where n is constant. On integrating Equation (17), we get

(18)

where a and b are constants of integration.

Using Equations (16) and (17) in (11), we obtain

(19)

which on solving yields

(20)

where C is constant of integration.

From Equation (20) and Figure 1 one can see that energy density is decreasing with evolution of the universe which is in fair agreement with observations.

On differentiating Equation (20), one can get

(21)

Now with the help of Equations (17) and (18), Equation (8) becomes

(22)

which on differentiation leads to

(23)

Substituting Equations (12), (14) and (17) into Equation (23), we have

(24)

By use of Equations (15) and (21), Equation (24) yields

(25)

where

From Equation (25) and Figure 2 one can see that gravitational constant is increasing with evolution of the universe which goes with observations.

Using Equations (20) and (25), Equation (22) gives

(26)

From Equation (26) and Figure 3 one can see that cosmological constant is decreasing with evolution of the universe which is in fair agreement with observations.

Now from Equations (15) and (20), we have

(27)

From Equation (27) and Figure 4 one can see that bulk viscosity coefficient is decreasing with evolution of the universe which is in fair agreement with observations.

From Equations (14) and (17), the expression for bulk viscous stress is given by

(28)

Thus the metric (1) reduces to the form

(29)

The shear scalar [41] may be defined as

(30)

For this model the Shear scalar is

(31)

From Equation (31) it is clear that as, shear dies out.

The expansion scalar is defined by

(32)

For this model expansion scalar is given by

(33)

The deceleration parameter is related to the expansion scalar as

(34)

For this model

(35)

Foe accelerating expansion of the universe the deceleration parameter q < 0 for

(36)

(37)

Case II: Causal Cosmological Solution

In addition to physically plausible relations (16), (17), in this case we assume

(38)

where H is Hubble parameter, given by

(39)

From Equations (17) and (39), the Hubble parameter is given by

(40)

Using Equations (17)-(18), (38) and (40) in Equation (8), we get

(41)

where

From Equations (20) and (41),

(42)

From Equation (42) and Figure 5 one can see that gravitational constant is increasing with evolution of the universe which supports observations.

Substitute the values from Equations (17), (20), (38) and (42) in Equation (5), we get

(43)

where

By use of Equation (20), Equation (43) gives

(44)

(i) Evaluation of Bulk viscosity in Truncated Causal Theory

Now we study variation of bulk viscosity coefficient and relaxation time with respect to the cosmic time. It has already been mentioned that for truncated theory and hence Equation (13) reduces to

(45)

In order to have exact solution of the system of equations one more physically plausible relation is required.

Thus, we consider the well known relation

(46)

Using Equations (17), (20), (44) and (46) in Equation (45) one can obtain

(47)

where

(ii) Evaluation of Bulk Viscosity in Full Causal Theory

It has already been mentioned that for full causal theory and hence Equation (13) reduces to

(48)

On the basis of Gibb’s inerrability condition, Maartens [40] has suggested the equation of state for temperature as

(49)

which with the help of Equation (16) gives

(50)

using Equations (20), (40), (46) and (50) in Equation (48) one can obtain

which on simplification yields the expression for bulk viscosity

(51)

4. Discussion

In this paper we have studied bulk viscous Bianchi type III space-time geometry with generalized Chaplygin gas and time-varying gravitational and cosmological constants. We have obtained a new set of Einstein’s equations

by considering and. In all cases energy density, bulk viscosity and cosmological

constant are decreasing as gravitational constant G(t) is increasing with time. Shear dies out with evolution of the universe for large value of t. For accelerating model of the universe, the deceleration parameter q < 0

for. We find that. Thus anisotropy is maintained throughout. However, if then, and then the model isotropizes. In case II for n = 1, we have

which is considered to be fundamental and match with the observations. In order to have clear idea of variation in behavior of cosmological parameters, relevant graphs have been plotted. All graphs of cosmological parameters go with cosmological observations.

Acknowledgements

S. K. would like to thank U. G. C. New Delhi for providing financial support under the scheme of major research project F. No. 41-765/2012 (SR). S. K. and R. K. would like to thank Inter University Centre for Astronomy and Astrophysics for providing facilities.

References