Natural Science
Vol.6 No.10(2014), Article
ID:46948,10
pages
DOI:10.4236/ns.2014.610071
Adaptive Match-Filtering: A Biomedical Application to Identify T-Wave Alternans
Laura Burattini1,2, Giovanni Ottaviano2, Francesco Di Nardo1, Sandro Fioretti1,2
1Department of Information Engineering, Università Politecnica delle Marche, Ancona, Italy
2B.M.E.D. Bio-Medical Engineering Development SRL, Università Politecnica delle Marche, Ancona, Italy
Email: l.burattini@univpm.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2014; revised 27 April 2014; accepted 4 May 2014
ABSTRACT
T-wave alternans (TWA), consisting in an alternation of the electrocardiographic (ECG) repolarization segment (T-wave), is a promising index of the risk of sudden cardiac death. By definition, it is characterized by a frequency component, termed fTWA, that matches half heart rate. The heartrate adaptive match filter (AMF) based method is a technique for automatic TWA identification from the digital ECG. Aim of the present study was to provide a complete technical description of the filter able to explain its methodological principles. The AMF is usually realized as a 6th order Butterworth filter with a narrow (0.12 Hz) passing band centered in fTWA. It is applied in a bidirectional fashion, so that final filtering order is 12. While extracting the TWA component, the AMF simultaneously filters out every ECG component including noise and artefacts, and thus results are very robust. Goodness of the technique was tested using 8 synthetic ECG tracings corrupted by typical noisy factors, such as white random noise, baseline wanderings, heart-rate variability, and others. Six ECG tracings were affected by 100 µV TWA, whereas two were not. Results indicate that the AMF-based method is able to prevent false-positive and false-negative detections and, thus, represents a useful tool for a reliable TWA identification.
Keywords:Adaptive Filtering, Digital ECG, T-Wave Alternans, Sudden Cardiac Death

1. Introduction
Despite recent advances in the treatment of life-threatening ventricular arrhythmias, sudden cardiac death (SCD; an unexpected death due to cardiac causes occurring within an hour of symptom onset in a person with known or unknown cardiac disease) remains one of the leading causes of death in developed countries [1] . At the present time, patients are selected for clinical evaluation and treatment of ventricular arrhythmias only after they have experienced and survived a major cardiac event. Thus, from a public health viewpoint, identification and treatment of such high-risk subjects before the occurrence of a cardiac event are expected to have a great impact on the problem of SCD [2] .
The simplest way to diagnose most of the cardiac abnormalities that can lead to SCD is to perform an electrocardiogram (ECG) test, which is noninvasive, painless and affordable, and provides a recording of the electrical activity of the heart by means of surface electrodes disposed on the skin in standardized positions. The ECG signal is, by its nature, an analog pseudo-periodical signal constituted by the repetition of a typical waveform-complex, representing a cardiac cycle (heartbeat) (Figure 1). At rest cardiac cells are polarized (electrically negative inside) but, if electrically stimulated, can temporally depolarize to generate the myocardium contraction. Under normal conditions, the electrical impulse is spontaneously generated by the sinoatrial node. Such impulse is then propagated throughout the right and left atria via the internodal tracts to stimulate the atrial myocardium contraction, generating the P wave. The internodal tracts end in the atrioventricular node which delays ventricular contraction, as represented by the PR segment. From the atrioventricular node the electrical impulse is propagated to the ventricles through the Bundle of His that splits into the left and right bundle branches, which further taper out into numerous Purkinje fibers to stimulate contraction of individual groups of myocardial cells. The spread of electrical activity through the ventricles is represented by the QRS complex, which also obscure most of atrial repolarization. Eventually, the ventricles repolarize, generating the electrocardiographic J wave, ST segment, and T and U waves. Nowadays most ECG recorders acquire the ECG signal in digital format, so that it can be stored in a computer memory and automatically processed for information extraction.
Among all the possible causes of SCD there are the abnormalities in the repolarization phase of the heart, which are known to be associated to susceptibility to malignant ventricular arrhythmias and SCD [3] . The standard indicator of cardiac safety in clinical trials is the QT interval [4] , which is measured as the time distance between the onset of the Q wave and the offset of the T wave, thus representing the total duration of the contraction and subsequent relaxation of the ventricles. The QT-interval measure, however, is strongly method- [5] and lead-dependent [6] , and thus little reliable. The difficulties in accurately measuring the QT interval, together with the clinical observation that not all pronged QT intervals necessarily lead to ventricular arrhythmias [7] , has stimulated the interest in identifying new alternative markers of abnormal repolarization [8] , among which microvolt T-wave alternans (TWA) is the most promising one [2] [9] -[16] .
T-wave alternans (TWA) consists in an alternation of the ECG T-wave amplitude on every-other-beat bases. Macroscopic (i.e. visible) forms of TWA are quite rare and may even show alternating T-wave polarity (Figure 2). Instead, microvolt forms of TWA are more common, but require specifically designed algorithms to be identified [17] -[19] because invisible to the naked eye. Both macroscopic and microvolt TWA have been associated to malignant ventricular arrhythmias and SCD [2] [9] -[16] .
The heart-rate adaptive match filter (AMF) based method is a popular technique for automatic TWA identification [20] . It is has been used in several comparative [18] [19] [21] and clinical studies [10] [22] -[26] , each of which has identified a specific peculiarity of the technique. Nevertheless, a detailed technical description of the filter, which allows a clear understanding of its methodological principles, has never been reported. Thus, aim
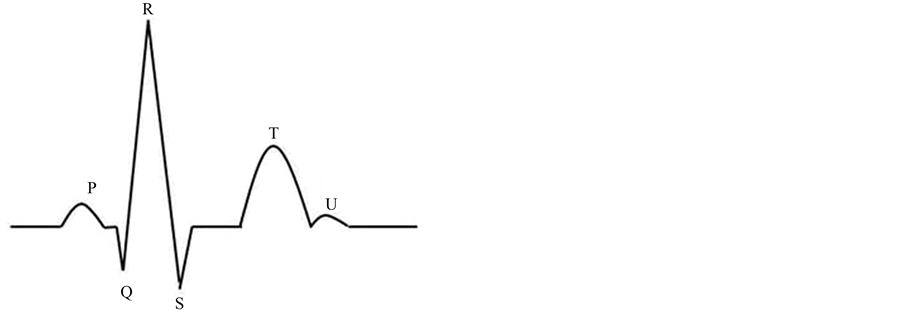
Figure 1. ECG complex relative to a single heartbeat showing all typical waves.
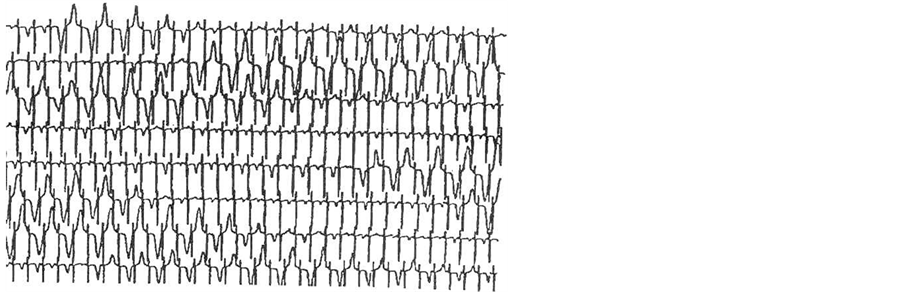
Figure 2. ECG affected by macroscopic, visible TWA with alternating T-wave polarity.
of the present study was to provide such a detailed AMF description. A simulation study was then used to demonstrate the goodness of the AMF-based method in identifying TWA in the typical noisy conditions usually affecting real ECG tracings.
2. The Heart-Rate Adaptive Match Filter Based Method
Ideally, at fixed heart rate (HR), TWA is characterized by a single frequency, by definition equal to half heart rate. However, in real clinical ECG tracings some physiologic HR variability always occurs. Consequently, the AMF-based method supposes TWA to be characterized by a small frequency band centered in half mean heart rate (fTWA), and conceives the AMF as a HR (and, thus, fTWA) adaptive narrow-band passing filter (ideally a match filter) with its passing band centered in fTWA. Its implementation consists of a 6th order bidirectional Butterworth band-pass filter characterized by a 0.12 Hz wide passing band centered in fTWA, which can be thought as cascade of a low-pass filter (LPF; cut-off frequency fLPF = fTWA + dfTWA, with dfTWA = 0.06 Hz) and a highpass filter (HPF; cut-off frequency fHPF = fTWA − dfTWA) [20] . The squared module of the AMF is expressed by the following equation:
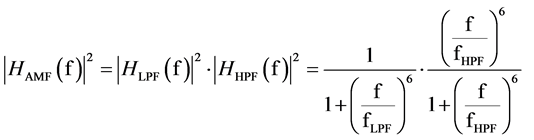 (1)
(1)
In the practical computerized applications involving digital ECG tracings the AMF has to be designed in the digital domain. To compute the digital AMF filter coefficients bi and ai (i = 0, 2… 6), bilinear transformation with frequency prewarping was used to convert the analog filter into a digital filter. Careful frequency adjustment guarantees that the analog filter and the digital filter will have the same frequency response magnitude at the cut-off frequencies. The AMF transfer function is reported in Equation (2), where the actual values of bi and ai parameters depend on HR and sample frequency (a1 = a3 = a5 = 0):
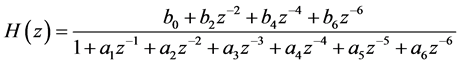 (2)
(2)
An example of digital AMF magnitude and phase responses relative to a mean HR of 80 bpm (or 1.33 Hz) and a sampling rate of 200 Hz is displayed in Figure 3. The magnitude response is a narrow passing band around 0.67 Hz, which corresponds to half HR, while the phase response is a non-linearly descending curve.
To avoid distortions due to the non-linearity of the phase response that causes the group delay not to be constant, the AMF is applied in a bidirectional fashion, that consists in a zero-phase digital filtering procedure performed by processing the input ECG data in both forward and reverse directions. The overall filter transfer function equals the squared magnitude of the original filter transfer function and doubles its order, so that actual filtering order becomes 12.
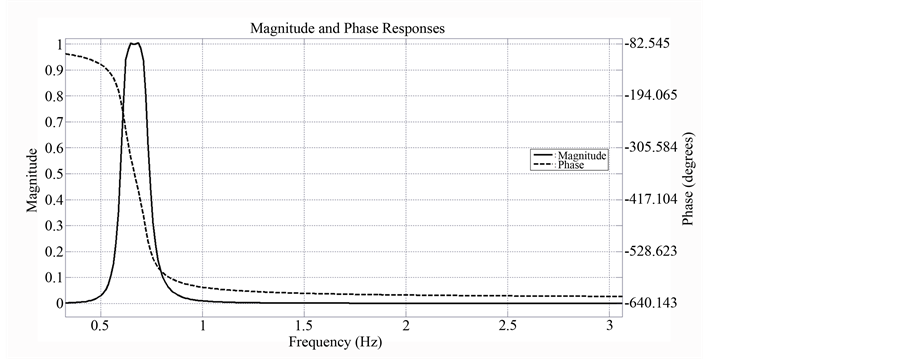
Figure 3. Digital AMF magnitude and phase responses relative to a mean HR of 80 bpm (fTWA = 0.67 Hz).
Each time the AMF is fed with an ECG, it first computes HR and corresponding fTWA, and then filters out every ECG components but the one relative to TWA. Thus, the output of the AMF is an amplitude-modulated sinusoidal signal, called the TWA signal, having the same length of the input ECG and characterized by a frequency which matches fTWA. If really pertaining to TWA (and not, for example, to QRS oscillations which match fTWA), the TWA signal maxima and minima have to fall inside in the ECG repolarization segment (ST segment and T-wave) (Figure 4). The local amplitude of the TWA signal in correspondence of the ith beat provides a quantification of the TWA amplitude (TWAAi, in µV) characterizing that beat. If the TWA signal has its maxima and minima outside the repolarization segment (as in the presence of QRS alternans, for example), the TWAAi values are set to zero (Figure 4). Eventually, in case of an ECG tracing affected by no alternans (of any kind), the TWA signal at the output of the AMF reduces to a zero constant signal. Consequently, all the TWAAi values are equal to zero. A global measure of TWA amplitude (TWAA) relative to an ECG tracing can be obtained by averaging all TWAAi values over the number of beats.
3. Simulation Study
3.1. Synthetic ECG Data
Basic tracing of our simulation set-up consisted of an N-fold (N = 64) repeated real digital (sampling rate: 200 Hz) ECG complex, 0.75 s long, with no visible noise and no baseline wanders. TWA fundamental frequency (fTWA) was 0.67 Hz, that is 1/(0.75 × 2 s) or 0.5 cycles per beat. T-wave was identified in a 160 ms window centered around the T-wave apex. When present, TWA was obtained increasing the T-wave amplitude of 100 µV. Globally, 8 synthetic ECG tracings were considered to include the most typical noise factors affecting clinical recordings (Figure 5):
Ÿ no TWA: ideal ECG tracing affected by no TWA and no noise;
Ÿ QRSA: ECG tracings affected by no TWA but by QRS alternans (QRSA) obtained by increasing the QRS amplitude of 100 µV;
Ÿ const TWA: ECG affected by a form of TWA which remains constant and equal to 100 µV;
Ÿ linear TWA: ECG affected by a form of TWA which linearly increases from 0 µV to 100 µV and linearly decreases from 100 µV to 0 µV;
Ÿ on-off TWA: ECG affected by a form of TWA which instantaneously increases from 0 µV to 100 µV;
Ÿ noise TWA: ECG tracing affected by constant 100 µV TWA and by zero-men white random noise of ± 100 µV in amplitude;
Ÿ baseline TWA: ECG tracing affected by constant 100 µV TWA and modulated with a sinusoidal baseline characterized by a frequency of 0.27 Hz (every 5 beats) and an amplitude of 100 µV.
Ÿ HRV TWA: ECG tracing affected by constant 100 µV TWA and by a HR variability (HRV) of ±25 ms around its mean value (0.75 s).
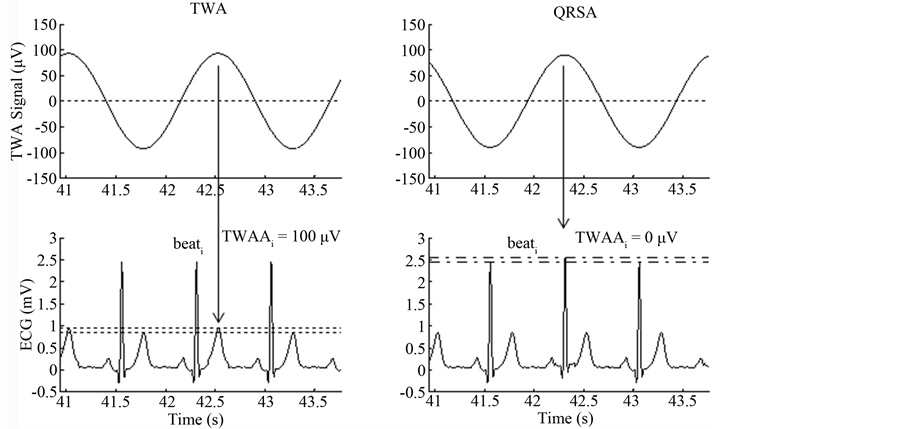
Figure 4. Example of T-wave alternans (TWA) and QRS alternans (QRSA).
3.2. Simulation Results
Application of the AMF to 8 synthetic ECG tracings provided the 8 TWA signals displayed in Figure 6. TWA signal was a zero-constant for the tracing affected by no TWA, while was sinusoidal (100 µV of amplitude) in the presence of QRSA. In the latter case, however, its maxima and minima did not occurred in correspondence of the ECG repolarization segment. Consequently, TWAA was found to be zero, analogously to what found for the former case (Figure 7). For the ECG characterized by constant TWA, a constant-amplitude sinusoidal TWA signal was extracted, which allowed identification of a constant TWA of 100 µV of amplitude (Figure 7). Amplitude modulated TWA signals were instead obtained for linearly and instantaneously changing TWA (Figure 6), which allowed identification values of TWAA close to the simulated ones (Figure 7). In particular estimated TWAA overcame the simulated values when TWA was linearly changing (errors between 6 and 22%), whereas it showed a transitory trend where the simulated one was instantaneously changing. Also in this latter case, estimated and simulated TWAA values were very close in correspondence of the ECG segments affected by stationary TWA (estimated TWAA was between 0 µV and 8 µV instead of zero for the first part of the ECG tracing, and above 90 µV in the second, with an error < 10%). Eventually, TWAA estimation was not significantly affected by the presence of noise (maximum error: 9%) and baseline wanderings (maximum error: 3%), whereas in the presence of HR variability the TWAA estimation error reached 20%.
4. Discussion
This study describes how adaptive match filtering can be used in a biomedical application finalized to TWA identification from digital ECG signals. TWA is a promising indicator of SCD ideally characterized by a frequency that, by definition, matches half HR (i.e. fTWA). Although TWA is an electrophysiological phenomenon which implies stable sinus rhythm, some small variations of the HR are usually acceptable, so that the phenomenon is more properly characterized by a very narrow band around fTWA. Thus, a heart-rate adaptive filter, with a narrow passing band appears as a useful tool to extract the frequency components characterizing TWA from an ECG tracing. While extracting the TWA signal, the AMF simultaneously filters out any other ECG component, including noise and artifacts. Because of this, the AMF-based method for TWA identification is a technique particularly robust to noise and interferences likely affecting real ECG tracings [21] . Still, other kinds of alternations, such as QRSA and some noise components, may fall in the narrow frequency band characterizing TWA, jeopardizing its correct identification. To minimize the probability of such occurrence, the phase of the TWA signal is analyzed before measuring its amplitude to determine TWAA. The maxima and the minima of the TWA signal, which is a pseudo-sinusoid, occur in correspondence of the center of mass of the alternations at fTWA present in the ECG signal. If such alternations mostly pertain to the T-waves, such maxima and minima must fall in correspondence of such waves. If this is not the case, TWA is not identified.
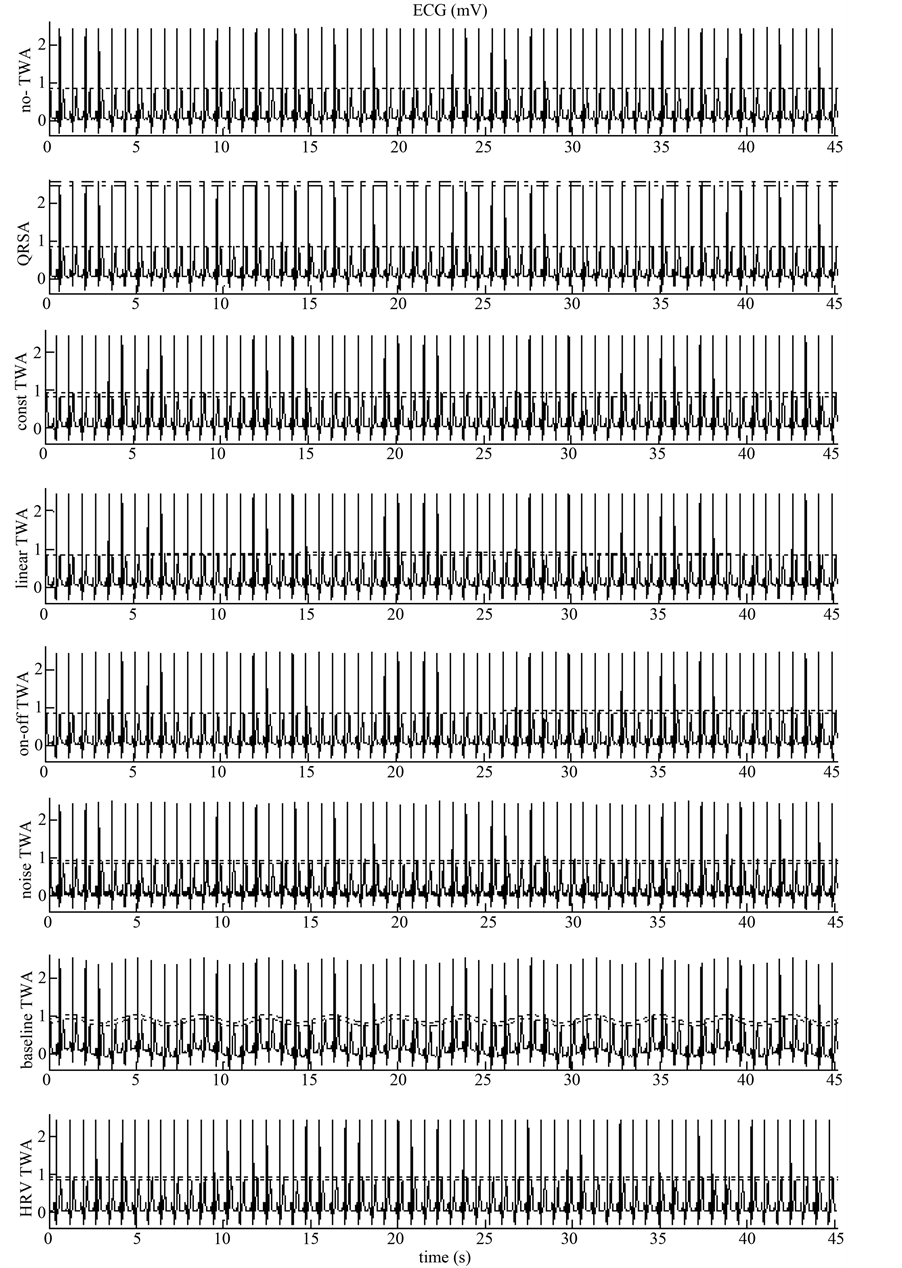
Figure 5. Synthetic ECG tracings (see text for details). Where present, TWA is highlighted by parallel dotted lines.
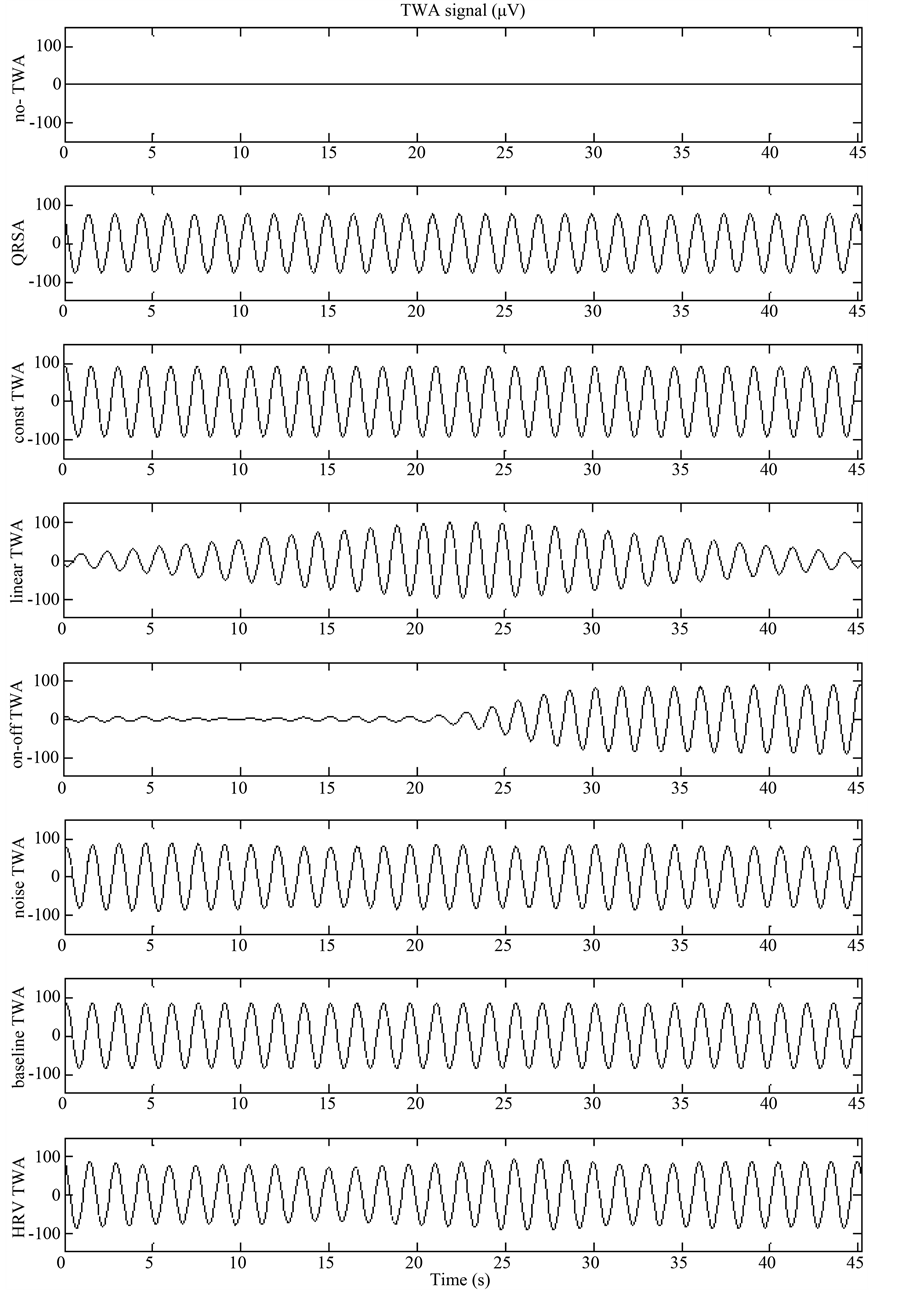
Figure 6. TWA signals at the output of the AMF when fed with the synthetic ECG tracings.
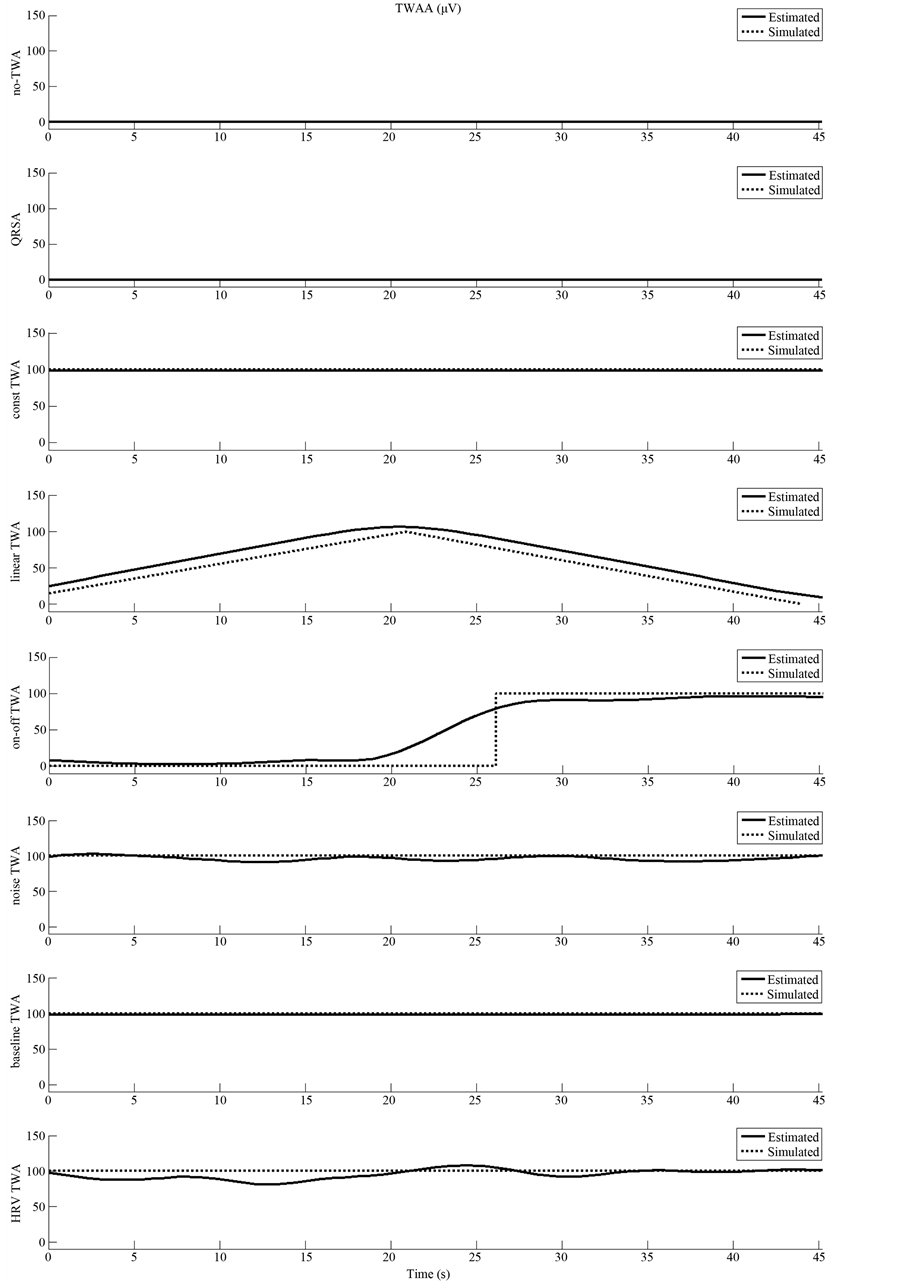
Figure 7. Estimated and simulated TWAA values in each synthetic ECG tracing.
Usually, the AMF is realized as a 6th order Butterwort filter, characterized by a magnitude response that is maximally flat in the pass-band and monotonic overall. The Butterworth filter sacrifices roll-off steepness for monotonicity in the passand stop-bands, but this is does not represents a limitation for the AMF. Indeed, it is applied bidirectionally, so that the final filtering order is 12, which is quite high for ECG applications (roll-off steepness increases with increasing filter order).
In the simulation study reported in this work, a MATLAB implementation of the AMF-method provided by B.M.E.D. Bio-Medical Engineering Development SRL (http://www.bmed-bioengineering.com) was used for TWA identification from synthetic ECG tracings affected by the most typical and representative noise factors. Results confirm the goodness of this technique in both avoiding false-positive as well as false-negative identifications, even though the presence of noise and interferences, such as HRV, may compromise perfect quantification of TWAA. The noise level and the baseline amplitude considered here were both 100 µV, i.e. equal to TWAA. Thus, the signal-to-noise ratio was low, around 1. In the worst corrupted conditions, the maximum error reported was 20% which does not represent a significant practical problem from a clinical point of view, since it is usually much more important to know if TWA is present or not and its order of magnitude rather than its exact amplitude. Very small levels of TWA (for example under 10 µV) are usually considered negligible, and could even be eliminated using a threshold criterion.
5. Conclusion
Heart-rate adaptive match filtering represents a useful technique for a reliable TWA identification from the digital ECG. The filter can efficiently be implemented using a digital 6th order narrow-passing-band Butterworth filter, which has to be specifically designed for each ECG tracing, since the passing band has centered around the fTWA, which is by definition, equal to half heart-rate. Given the non-linearity of the phase response, the filter has to be applied in a bidirectional fashion to avoid signal distortions.
References
- Montagnana, M., Lippi, G., Franchini, M., Targher, G. and Cesare Guidi, G. (2008) Sudden Cardiac Death: Prevalence, Pathogenesis, and Prevention. Annals of Medicine, 40, 360-375. http://dx.doi.org/10.1080/07853890801964930
- Rosenbaum, D.S., Albrecht, P. and Cohen, R.J. (1996) Predicting Sudden Cardiac Death from T Wave Alternans of the Surface Electrocardiogram: Promise and Pitfalls. Journal of Cardiovascular Electrophysiology, 7, 1095-111.
- Hlaing, T., DiMino, T., Kowey, P.R. and Yan, G.X. (2005) ECG Repolarization Waves: Their Genesis and Clinical Implications. Annals of Noninvasive Electrocardiology, 10, 211-223. http://dx.doi.org/10.1111/j.1542-474X.2005.05588.x
- Zhang, Y., Post, W.S., Blasco-Colmenares, E., Dalal, D., Tomaselli, G.F. and Guallar, E. (2011) Electrocardiographic QT Interval and Mortality: A Meta-Analysis. Epidemiology, 22, 660-670. http://dx.doi.org/10.1097/EDE.0b013e318225768b
- Malik, M. (2004) Errors and Misconceptions in ECG Measurement Used for the Detection of Drug Induced QT Interval Prolongation. Journal of Electrocardiology, 37, 25-33. http://dx.doi.org/10.1016/j.jelectrocard.2004.08.005
- Malik, M. and Batchvarov, V.N. (2000) Measurement, Interpretation and Clinical Potential of QT Dispersion. Journal of the American College of Cardiology, 36, 1749-1766. http://dx.doi.org/10.1016/S0735-1097(00)00962-1
- Hondeghem, L. (2006) Thorough QT/QTc Not So Thorough: Removes Torsadogenic Predictors from the T-Wave, Incriminates Safe Drugs, and Misses Profibrillatory Drugs. Journal of Cardiovascular Electrophysiology, 17, 337-340.
- Brennan, T.P. and Tarassenko, L. (2012) Review of T-Wave Morphology-Based Biomarkers of Ventricular Repolarisation Using the Surface Electrocardiogram. Biomedical Signal Processing and Control, 7, 278-284. http://dx.doi.org/10.1016/j.bspc.2011.05.010
- Hou, Y., Fang, P.-H., Wu, Y., Li, X.-F., Liu, J., Li, Z., Lei, S. and Shu, Z. (2012) Prediction of Sudden Cardiac Death in Patients after Acute Myocardial Infarction Using T-Wavealternans: A Prospective Study. Journal of Electrocardiology, 45, 60-65. http://dx.doi.org/10.1016/j.jelectrocard.2011.07.015
- Man, S., De Winter, P.V., Maan, A.C., Thijssen, J., Borleffs, C.J. van Meerwijk, W.P., Bootsma, M., van Erven, L., van der Wall, E.E., Schalij, M.J., Burattini, L., Burattini, R. and Swenne, C.A. (2011) Predictive Power of T-Wave Alternans and of Ventricular Gradient 2 Hysteresis for the Occurrence of Ventricular Arrhythmias in Primary Prevention ICD Patients. Journal of Electrocardiology, 44, 453-459. http://dx.doi.org/10.1016/j.jelectrocard.2011.05.004
- Leino, J., Minkkinen, M., Nieminen, T., Lehtim?ki, T., Viik, J., Lehtinen, R., Nikus, K., K??bi, T., Turjanmaa, V., Verrier, R.L. and K?h?nen, M. (2009) Combined Assessment of Heart Rate Recovery and T-Wave Alternans during Routine Exercise Testing Improves Prediction of Total and Cardiovascular Mortality: The Finnish Cardiovascular Study. Heart Rhythm, 6, 1765-1771. http://dx.doi.org/10.1016/j.hrthm.2009.08.015�
- Maeda, S., Nishizaki, M., Yamawake, N., Ashikaga, T., Shimada, H., Asano, M., Ihara, K., Murai, T., Suzuki, H., Fujii, H., Sakurada, H., Hiraoka, M. and Isobe, M. (2009) Ambulatory ECG-Based T-Wave Alternans and Heart Rate Turbulence Predict High Risk of Arrhythmic Events in Patients with Old Myocardial Infarction. Circulation Journal, 73, 2223-2228. http://dx.doi.org/10.1253/circj.CJ-09-0420
- Sakaki, K., Ikeda, T., Miwa, Y., Miyakoshi, M., Abe, A., Tsukada, T., Ishiguro, H., Mera, H., Yusu S. and Yoshino, H. (2009) Time-Domain T-Wave Alternans Measured from Holter Electrocardiograms Predicts Cardiac Mortality in Patients with Left Ventricular Dysfunction: A Prospective Study. Heart Rhythm, 6, 332-337. http://dx.doi.org/10.1016/j.hrthm.2008.12.011
- Hohnloser, S.H. (2008) T-Wave Alternans: A Pathophysiological Link to Human Ventricular Tachyarrhythmias. Heart Rhythm, 5, 677-678. http://dx.doi.org/10.1016/j.hrthm.2008.02.023
- Stein, P.K., Sanghavi, D., Domitrovich, P.P., Mackey, R.A. and Deedwania, P. (2008) Ambulatory ECG-Based TWave Alternans Predicts Sudden Cardiac Death in High-Risk Post-MI Patients with Left Ventricular Dysfunction in the EPHESUS Study. Journal of Cardiovascular Electrophysiology, 19, 1037-1042. http://dx.doi.org/10.1111/j.1540-8167.2008.01225.x
- Klingenheben, T., Zabel, M., D’Agostino, R.B., Cohen, R.J. and Hohnloser, S.H. (2000) Predictive Value of T-Wave Alternans for Arrhythmic Events in Patients with Congestive Heart Failure. Lancet, 356, 651-652. http://dx.doi.org/10.1016/S0140-6736(00)02609-X
- Martínez, J.P. and Olmos, S. (2005) Methodological Principles of T Wave Alternans Analysis: A Unified Framework. IEEE Transactions on Biomedical Engineering, 52, 599-613. http://dx.doi.org/10.1109/TBME.2005.844025
- Bini, S. and Burattini, L. (2013) Quantitative Characterization of Repolarization Alternans in Terms of Amplitude and Location: What Information from Different Methods? Biomed Signal Process Control, 8, 675-681. http://dx.doi.org/10.1016/j.bspc.2013.06.012
- Burattini, L., Bini, S. and Burattini, R. (2009) Comparative Analysis of Methods for Automatic Detection and Quantification of Microvolt T-Wave Alternans. Medical Engineering & Physics, 31, 1290-1298. http://dx.doi.org/10.1016/j.medengphy.2009.08.009
- Burattini, L., Zareba, W. and Burattini, R. (2008) Adaptive Match Filter Based Method for Time vs. Amplitude Characterization of Microvolt ECG T-Wave Alternans. Annals of Biomedical Engineering, 36, 1558-1564. http://dx.doi.org/10.1007/s10439-008-9528-6
- Burattini, L., Bini, S. and Burattini, R. (2011) Automatic Microvolt T-Wave Alternans Identification in Relation to ECG Interferences Surviving Preprocessing. Medical Engineering & Physics, 33, 17-30. http://dx.doi.org/10.1016/j.medengphy.2010.08.014
- Burattini, L., Zareba, W. and Burattini, R. (2009) Assessment of Physiological Amplitude, Duration and Magnitude of ECG T-Wave Alternans. Annals of Noninvasive Electrocardiology, 14, 366-374. http://dx.doi.org/10.1111/j.1542-474X.2009.00326.x
- Burattini, L., Zareba, W. and Burattini, R. (2010) Identification of Gender-Related Normality Regions for T-Wave Alternans. Annals of Noninvasive Electrocardiology, 15, 328-336. http://dx.doi.org/10.1111/j.1542-474X.2010.00388.x
- Burattini, L., Bini, S. and Burattini, R. (2012) Repolarization Alternans Heterogeneity in Healthy Subjects and Acute Myocardial Infarction Patients. Medical Engineering & Physics, 34, 305-312. http://dx.doi.org/10.1016/j.medengphy.2011.07.019
- Burattini, L., Man, S., Burattini, R. and Swenne, C.A. (2012) Comparison of Standard vs. Orthogonal ECG Leads for T-Wave Alternans Identification. Annals of Noninvasive Electrocardiology, 17, 130-140. http://dx.doi.org/10.1111/j.1542-474X.2012.00490.x
- Burattini, L., Man, S. and Swenne, C.A. (2013) T-Wave Alternans Dependency on T-Wave Amplitude in Exercise Electrocardiographic Recordings. International Journal of Bioelectromagnetism, 15, 90-96.

