Natural Science
Vol.06 No.17(2014), Article ID:52903,6 pages
10.4236/ns.2014.617119
Using the Resistance Depending on the Magnetic and Electric Susceptibility to Derive the Equation of the Critical Temperature
H. G. I. Hamza1, M. H. M. Hilo2, R. Abd Elgani2, R. Abd Elhai2, Mubarak Dirar2
1Department of Physics, Gazera University, Hasahisa, Sudan
2Department of Physics, Sudan University of Science and Technology, Khartoum, Sudan
Email: hasabo25@hotmail.com, mhhlo@qu.edu.sa, mahmoud1972@sustech.edu, rawia@sustech.edu, rashaabdelhaye@sustech.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 September 2014; revised 20 October 2014; accepted 15 November 2014
ABSTRACT
In this study the electromagnetic theory and quantum mechanics are utilized to find the resistivity in terms of electric and magnetic susceptibility in which the electron is considered as a wave. Critical temperature of the wire at which the resistance vanishes is found. In this case the resistance being imaginary which leads the real part of the resistance to real zero at critical temperature and the material becomes super conductor in this case. If one considers the motion of electron in the presence of inner magnetic field and resistance force, a new formula for the conductivity is to be found; this formula states that the material under investigation becomes a superconductor at critical temperature and depends on the strength of the magnetic field and friction resistance, and the substance conductivity is found to be super at all temperatures beyond the critical temperature.
Keywords:
Susceptibility, Superconductivity, Critical Temperature, Permeability, Permittivity

1. Introduction
In superconductors, the resistance is zero at temperatures less than the critical temperature [1] ; in this work, the above concept is proved by taking the conductivity as a function of the permittivity and permeability, and within the existence of the conditions that make the resistance be equal to zero or approach to infinity.
2. Resistivity Formula Due to the Permeability and Permittivity
When the temperature of a conductor approach to the absolute zero, the friction resistance can be ignored [2] , if an electron e is induced by an electric field E, then the force on it is given by
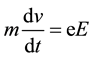 (1)
(1)
Including the position variable  in Equation (1) it can be written as
in Equation (1) it can be written as
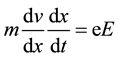 (2)
(2)
Then
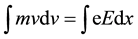 (3)
(3)
According to the definition of the potential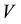 , we get
, we get
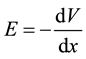 (4)
(4)
From Equation (3)
 (5)
(5)
Then
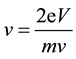 (6)
(6)
While  is constant, and when the potential difference is constant, then the velocity
is constant, and when the potential difference is constant, then the velocity  is being also constant.
is being also constant.
Using Equation (6) and substituting the value of  in the equation of current, that given due to the electron velocity
in the equation of current, that given due to the electron velocity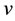 , charges density
, charges density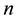 , and the area
, and the area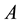 ,
, 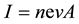 , then the current
, then the current 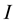 is found to be
is found to be

Then the resistance 

On other hand 



Considering the electron as a wave, its velocity becomes [3]

Accordingly the resistivity is given by

3. Critical Temperature at a Changing Permeability µ
If a magnetic field with a flux density


force 

where 

where 
when the outer magnetic field vanishes, then the radial velocity becomes

And

where 
And when an outer magnetic field 

where 



The equation of motion in the presence of the outer magnetic field is given in the form [5] .

where 


when 


where 
Dividing both sides by 


The current for one atom with 

where 


The magnetic torque for one atom is given by

where 
And from Figure 1, one get:
But

So the magnetic torque for one atom 
Figure 1. Magnetic torque in Z direction.

If the number of atoms per unit volume is assumed to be 


According to the definition of susceptibility 

Comparing Equations (26) and (27) the susceptibility being

Then the resistivity in Equation (11) becomes

where 
The resistivity 
or 
Accordingly the critical temperature becomes
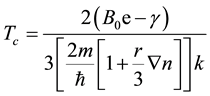
4. Calculating the Critical Temperature Due to the Conductivity
Assuming that the charges in the conductor are acted by a resistance force



The previous forces are given by the formulas
where 

The equation of motion takes the formula

When the electron moves with a uniform constant velocity, the Equation (33) becomes

And the conductivity is given by

where 


And the conductivity approaches to infinity when

According to the Maxwell-Boltzmann statistics the density of the atoms in the medium takes the formula [8] .
Then

Equation (38) represents the critical temperature in which the conductivity becomes very huge, and when

The conductivity also becomes very high, and then


And finally the critical temperature is found to be

5. Discussion
The classical rules of the electron motion in Equation (1) are used to find the classical formula of the resistivity given in Equation (11), and the electron is considered to be a wave according to the quantum principles and this clarified that the resistivity is a function of the electric and magnetic susceptibility.
The interpretation of Equation (28)―in which we derived the magnetic susceptibility from the electron equation of motion, that depend on the friction force within the friction coefficient







When we considered the electron motion due to the impact of an inner magnetic field, and a friction resistance, the conductivity was found to be as shown in Equation (36).
The mathematical analysis interprets that the conductivity becomes very high at temperatures less than the critical temperature, which depends on the friction resistance and the inner magnetic field as shown in Equations (41)-(42).
6. Conclusion
The model in which the resistance depends on the electric and magnetic susceptibility, clarifies that the resistance vanishes, and the metal becomes a superconductor at the critical temperature and the temperatures less than it; this relation is not clear in the famous models of the superconductivity.
References
- Sales, B.C., et al. (2012) Transport, Thermal, and Magnetic Properties of the Narrow Gap Semiconductor CrSb2. Physical Review B, 86, Article ID: 235136. http://dx.doi.org/10.1103/PhysRevB.86.235136
- Nguyen, D.N., et al. (2009) Temperature Dependence of Total AC Loss in High-Temperature Superconducting Tapes. IEEE Transactions on Applied Superconductivity, 19, 3637-3644.
- Slooten, E., et al. (2009) Enhancement of Superconductivity near the Ferromagnetic Quantum Critical Point in UCoGe. Physical Review Letters, 103, Article ID: 097003.
- Millican, J.N., Phelan, D., Thomas, E.L., Leao, J.B. and Carpenter, E. (2009) Solid State Communications, 149, 707.
- Kantorovich, L. (2004) Quantum Theory of the Solid State: An Introduction. Kluwer Academic Publishers, London. http://dx.doi.org/10.1007/978-1-4020-2154-1
- Weyeneth, S., Puzniak, R., Mosele, U., Zhigadlo, N.D., Katrych, S., Bukowski, Z., Karpinski, J., Kohout, S., Roos, J. and Keller, H. (2009) Anisotropy of Superconducting Single Crystal SmFeAsO0.8F0.2 Studied by Torque Magnetometry. Journal of Superconductivity and Novel Magnetism, 22, 325-329. http://dx.doi.org/10.1007/s10948-008-0413-1
- Weyeneth, S., Puzniak, R., Zhigadlo, N.D., Katrych, S., Bukowski, Z., Karpinski, J. and Keller, H.J. (2009) Evidence for Two Distinct Anisotropies in the Oxypnictide Superconductors SmFeAsO0.8F0.2 and NdFeAsO0.8F0.2. Journal of Superconductivity and Novel Magnetism, 22, 347-351. http://dx.doi.org/10.1007/s10948-009-0445-1
- De Visser, A., et al. (2009) Muon Spin Rotation and Relaxation in the Superconducting Ferromagnet UCoGe. Physical Review Letters, 102, Article ID: 167003. http://dx.doi.org/10.1103/PhysRevLett.102.167003
















