Natural Science
Vol.06 No.06(2014), Article ID:44855,21 pages
10.4236/ns.2014.66041
Gibbs Density Surface of Water and Steam: 2nd Debate on the Absence of Van Der Waals’ “Critical Point”
Leslie V. Woodcock
Department of Physics, University of Algarve, Faro, Portugal
Email: lvwoodcock@ualg.pt
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 January 2014; revised 2 March 2014; accepted 10 March 2014
ABSTRACT
A revised phase diagram for water shows three distinct fluid phases. There is no continuity of liquid and gas, and no “critical point” on Gibbs’ density surface as hypothesized by van der Waals. A supercritical colloidal mesophase bounded by percolation transition loci separates supercritical liquid water and gas-phase steam. The water phase is bounded by a percolation transition (PA) of available volume, whereas steam is bounded by the loci of a percolation transition (PB) at a density whereupon a bonded molecular cluster suddenly percolates large distances. At the respective percolation densities, there is no barrier to nucleation of water to steam (PA) or steam to water (PB). Below the critical temperature, the percolation loci become the metastable spinodals in the two-phase coexistence region. A critical divide is defined by the interception of PA and PB the p-T plane. Critical parameters are obtainable from slopes and intercepts of pressure-density supercritical isotherms within the mesophase. The supercritical mesophase is a fourth equilibrium state besides ice, water and steam. A thermodynamic state function rigidity (dp/dρ)T defines a distinction between liquid and gas, and shows a remarkable symmetry due to an equivalence in number density fluctuations, arising from available volume and molecular clusters, in liquid and gas respectively. Following an earlier debate in these pages [“Fluid phases of argon: A debate on the absence of van der Waals’ critical point” Natural Science 5 (2) 194-206 (2013)], we here report further debate on a science of criticality applied to water and steam (APPENDIX 1).
Keywords:
Water, Steam, Phase Diagram, Critical Line, Percolation Loci

1. Introduction
The thermodynamic diagram of water phases is described in a recent educational review [1] . Theoretical and computational advances, however, have done little to change the generally accepted phase boundaries of water and steam over many decades [2] . A wide variety of water phase diagrams in various projections of Gibbs surfaces for state functions of temperature (T) and pressure (p) can be viewed on comprehensive websites [3] . They show no boundaries between the phases of water and steam as they merge above the critical temperature. Some show ad hoc dividing lines using the critical isotherm, others the critical isobar, to bound “water” and “steam” from a supercritical “fluid”, but these lines have no thermodynamic status.
The conventional phase diagram of water, and indeed all other pure fluids, is presently based upon the van der Waals hypothesis [4] . Briefly, every fluid there is deemed to exist a critical temperature-pressure singularity at Tc,pc where upon an equation-of-state for which the first two derivatives of pressure, i.e. with respect to changes in volume at constant T, go to zero. This has been the accepted description of liquid-gas criticality since van der Waals published his renowned thesis “On the continuity of liquid and gas”. The hypothesis further implies that for all supercritical temperatures the thermodynamic state functions e.g. density ρ(T,p) or Gibbs energy G(T,p), from the gas at low density, steam, to the liquid at high density, water, are continuous in all their derivatives for supercritical temperatures across the whole density range.
Another hypothesis that has been fashionable amongst theoretical physicists for about 50 years is the concept of universality [5] . From Ising models, ferro-magnetic systems, spin glasses, to liquid-gas criticality, according to this community, all critical phenomena, obey the same universal physical description, in the vicinity of a “critical point”, which can be explained using group renormalization theory [5] . An originator of this theory, K. Wilson, summarizes the phenomenology of liquid-gas criticality by reference to water and steam in one brief paragraph as follows [6] :
“A critical point is a special example of a phase transition. Consider, e.g. the water-steam transition. Suppose that water and steam are placed under pressure always at the boiling temperature. At the critical point, the distinction between water and steam disappears, and the whole boiling phenomena vanishes. The principal distinction between water and steam is that they have different densities. As the pressure and temperature approach their critical values the difference in density between water and steam goes to zero”.
It is evident from modern 5-figure precision density data (Figure 1), that Wilson’s assertion does not accord with experiment. Recent investigations, moreover, of percolation transitions in model square-well fluids [7] [8] , also contradict this hypothesis. We have concluded that, at the critical temperature Tc, the density difference does not go to zero. Rather, we have found that a liquid-gas critical “point”, as hypothesised by van der Waals and accepted by the physics community for 140 years, does not exist a such. Moreover, there is no universality of critical phenomena that spans the dimensions. In the ρ(T,p) surface there is a dividing line of uniform
Figure 1. Densities of saturated water and steam vapour in the vicinity of the critical temperature taken from IAWPS?IF97 Electronic Steam Tables (see reference [11] ).The nearest data point to Tc is at 373.8˚C, i.e. within 0.1 K of the critical temperature (373.9˚C) from the same source; the critical density values are intercepts given by the EXCEL cubic trendlines with the constants representing the critical coexistence densities.
chemical potential connecting maximum and minimum coexisting gas and liquid densities, respectively, above which there exists a supercritical mesophase bounded by weak higher-order percolation transitions, and below which there is the familiar liquid-vapour coexistence region. Furthermore, and contrary to Wilson’s statement above [6] , for T > Tc water and steam remain distinctly different phases, and are separated by a supercritical mesophase.
This new description of liquid-gas criticality has also been shown to describe all the experimental thermodynamic phenomenology of liquid and gaseous argon [9] . Water and steam exhibit essentially the same phenomenology as fluid phases of argon [5] [6] . Moreover, for temperatures above the critical temperature the phases of water and steam exist with distinct liquid and gas properties, and are separated by a supercritical mesophase (formerly referred to as “steam II” [8] ). The mesophase can be characterized as being macroscopically homogeneous, but microscopically heterogeneous colloidal-like mixture of gas-like molecules and molecular clusters, and liquid-like macroscopic clusters or droplets, all with the same Gibbs chemical potential. These phase boundaries appear as a weak higher-order thermodynamic phase transition, known as percolation transition loci, on the Gibbs state function f(T,p) surfaces [7] -[9] . They were unforeseen by Gibbs, but recently have been shown to play a role in determining the phase diagram alongside Gibbs phase rule [10] .
2. Percolation Transitions
Percolation transitions occur when structural properties of a molecular system, for example clusters of molecules in the gas phase, or holes in the liquid phase, on reaching a certain density suddenly coalesce from being of molecular dimension to become macroscopic, i.e. system spanning. This gives rise to higher-order thermodynamic phase transitions, in which there are discontinuities in second and/or higher derivatives of Gibbs chemical potential (μ) with respect to temperature or pressure, notably: isothermal compressibility (d2μ/dp2)T, heat capacity (d2μ/dT2)p and thermal expansivity (d2μ/dpdT) all of which undergo some degree of change at, or in the vicinity of, percolation transitions.
We begin therefore by taking a look at the behaviour of these three second-order thermodynamic state functions in the case of supercritical water (Figure 2).
The first observation from Figure 2 is that all three derived properties exhibit a line of maximum values stemming from the coexistence line at Tc. The observation of these lines has a long history that goes back to J. D. Bernal [12] . They are characterized in the literature, but have remained somewhat of a mystery. Bernal actually named the line of maximum heat capacity (Cp), which can be clearly observed in Figure 2(a), as the “hypercritical line”. It appears to be the extension of the coexistence line. The maximum in the thermal expansivity (αp) (Figure 2(b)) is shifted, very slightly to higher temperature from Bernal’s hypercritical line; it is not quite the same line. Likewise, the line of maximum isothermal compressibility Figure 2(c), which has been referred to as the Widom line [13] is also shifted even further to higher temperatures. Interestingly, these three supercritical loci have been rediscovered recently in molecular simulations of Lennard-Jones fluids [14] . Associated lines of maxima in various dynamical properties have also been reported [15] , a Russian name has even been suggested for another such line discovered recently [16] .
The second observation that we make from Figure 2 is that there is a clear difference in thermodynamic behavior between steam, at pressures below the coexistence-hypercritical line, and water above it. In the liquid phase, Cp, αp and κT, all increase with temperature along an isobar, whereas in the gaseous state they all decrease with temperature. Thus there is a fundamental thermodynamic defining distinction between liquid and gas that extends to supercritical temperatures. Below, we find that defining property is the work required to change the density, i.e.an inverse compressibility, or rigidity (dp/dρ)T where ρ is the density. The rigidity of a gas decreases with density and increases for a liquid, i.e. (d2p/dρ2)T is negative for a gas and positive for a liquid; its value is zero in the mesophase. Lines of higher-order discontinuity in the rigidity can be characterized, not just for water, but all liquids, in terms of percolation loci that bound the supercritical mesophase separating gas from liquid.
Percolation transitions in model fluids of hard-spheres and square-well molecules are well defined by a characteristic distance, which unambiguously divides configuration space volume into “sites” and “holes”. The densities at which small clusters of occupied sites in the gas phase, or unoccupied holes in the liquid phase, first span the whole system are referred to as percolation transitions, and denoted by PB and PA, referring to “bonded cluster” (sites) and “available volume” (holes) respectively [7] -[9] . For model fluids with continuous pair potentials, and all real fluids, however, there is no such well-defined distance to define PA and PB. In the case of
Figure 2. Isocontours for water and steam: (a) heat capacity (Cp); (b) thermal expansivity (αp) (c) isothermal compressibility (κT): from International Steam Tables [11] .
water, however, the steep hydrogen bond is fairly sharply defined for water clusters. At a given temperature, the total volume of any equilibrium configuration of water or steam can be divided in occupied sites, not accessible to an incoming molecule, and holes which would be accessible to an additional molecule. At these percolation transitions, thermodynamic state functions can change form due to sudden changes in the state-dependence of density and/or energy fluctuations. It is the change in (dp/dρ)T that defines PA and PB phenomenologically.
In order to understand “mysterious lines” [12] [16] on the p(T) projection, we first look at the discontinuities in the Gibbs density surface which reflect the percolation loci PA and PB. These can be seen in Figure 3, in which various supercritical isotherms from the International Steam Tables of Wagner and Krezschmar [11] are plotted and analyzed for the three supercritical phases, as in a previous analysis of liquid argon [9] The bonded-cluster percolation transition (PB) occurs when atoms bonded together in molecular clusters, within a characteristic distance, e.g. close to the hydrogen-bond length, suddenly begin to be macroscopic. At a higher pressure and density, the available volume percolation transition (PA) occurs at a density below which the distribution of “holes” in the liquid suddenly begins to permeate the volume or become macroscopic.
The critical divide from Figure 1 at Tc is shown in Figure 3 from the experimental p-ρT data [11] ; the percolation loci must pass through these two points. The data points used to estimate the region of the mesophase, i.e. stemming from the two percolation transitions at Tc, are obtained from the EXCEL trend line fits to the densities of water and steam in Figure 1 The lowest temperature in Figure 3, T = 370, is subcritical (Tc = 374˚C). The percolation transitions define the limits of existence of the supercritical steam and water phases on the Gibbs density surface.
3. Phase Limits of Steam and Water
Both percolation transitions can be observed on all the supercritical isotherms as a weak discontinuity in the slope of the p(ρ) isotherms. For temperatures up to 800˚C, all the isotherms show three distinctly different
Figure 3. Experimental data points for the p-ρ isotherms of supercritical water from the IAPWS-International Steam Tables [5] . The extended straight lines, fitted in the intermediate linear region for the two isotherms 450 and 500, have been superimposed to highlight the higher-order discontinuities associated with percolation transition loci PB and PA,approximately illustrated by vertical dashed lines at the critical coexisting densities in Figure 1.
regions of behavior for the state function p(ρ)T. In the steam phase ρ < ρPB the rigidity (dp/dρ)T decreases with density, in the mesophase ρPB < ρ < ρPA(dp/dρ)T is constant, and for water ρ > ρPA and (dp/dρ)T increases with density. The slope of the isotherm in the mesophase is zero at the critical temperature. This fundamental extensive state function, called “rigidity”, is the work required to change the density reversibly, with the dimensions of a molar energy, hence equal to the change in Gibbs energy (G) with density
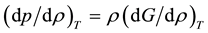 (1)
(1)
It will eventually explain all the mysterious maxima in Figure 2, the percolation loci in Figure 3, the nature of the supercritical mesophase. Rigidity, moreover, defines a distinction between steam and water or, more generally, between gas and liquid.
The reason for linearity of p(ρ) in the mesophase, can be understood if the percolation loci, although lacking a definition at the molecular level, are defined phenomenologically similar to subcritical spinodal lines. The limit of existence of the gas phase (PB) corresponds to the density (ρPB) at which the first system-spanning cluster of “occupied sites” or stable liquid state “nucleite” spontaneously appears in equilibrium configurations. The chemical potential of the small cluster species in the gas phase, becomes equal to the chemical potential of a liquid “droplet” at a higher pressure. At this density the gas phase ceases to exist as such, and for densities above ρPB, i.e. in the mesophase, the fluid is essentially a homogeneous mixture of gaseous molecules, i.e. dimers, trimers and small clusters, etc. plus liquid-like macro clusters. There is a bimodal distribution of cluster sizes [9] .
Likewise, as the liquid state density is reduced across PA, from above ρPA to below ρPA, the “unoccupied holes” spontaneously coalesce to form system-spanning “holes” of gas which can contain single molecules, or small clusters, which will have the same chemical potential as the liquid, albeit at the lower gas phase pressure. Thus, in this region there are larger fluctuations in energy, pressure and density that explains the maxima loci of Cp, αp and κT in Figure 2 and references [12] -[16] .
The discontinuities in (dp/dρ)T, and linearity of (dp/dρ)T in the mesophase region, seen in Figure 3, has been simply explainedby a linear combination rule. It is essentially a supercritical extension of the subcritical two- phase Lever rule. The structural properties of the mesophase in the vicinity of Tc and PB will resemble a liquid- in-gas “mist” with wide polydispersity of the micro-droplets, whereas in the vicinity of PA a colloid with water being the continuous phase, and steam dispersed rather like small bubbles as in a gas-in-liquid “foam”. The different refractive index and size distribution of a dispersed phase give rise to a supercritical opalescence, or white appearance, known in colloid science as Tyndall scattering [17] .
For temperatures below Tc, PA and PB become the metastable spinodals of liquid to gas, and gas to liquid, spontaneous nucleation loci respectively. Both above and below the critical divide at Tc, PA and PB represent the limits of existence of the liquid water and gaseous steam phases respectively.
Another feature of second or higher-order phase transitions, which is consistent with thermodynamic properties, is the non-existence of supercritical metastability. Whereas first-order phase transitions on Gibbs density surfaces are characterized by a possible metastable existence of either phase on both sides of the transition point of equal chemical potential, there can be no metastability across a second-order phase transition. The reason being since, in a higher-order transition, (dp/dρ)T is the same for both phases at the point of the transition it follows from equation (1) that the phase with the higher rigidity would have a lower chemical potential, and hence be the more stable, on both sides of the transition on the Gibbs density surface. Since this is a thermodynamic impossibility, PA and PB loci are minima and maxima density limits for the existence of the liquid and gas phases, respectively.
4. Critical Parameters
Supercritical isotherms for experimental ρ(p,T) data in the near-critical mesophase region can be used to obtain independent critical parameters without resort to experimental data in the two-phase region. In this section we perform the same analysis that resulted in the determination or revised critical properties of argon, but the present exercise is less accurate as there are fewer data points on each isotherm in the tables used [11] .
Every supercritical isotherm, shown for example in Figure 3, in the mesophase region, obeys the linear equation for the pressure with a high precision within the bounds of uncertainty. The linear equation
 (2)
(2)
where Rm is the constant isothermal rigidity (dp/dρ)T within the mesophase. It is independent of density, and as shown in Figure 4, can be easily parameterized. Slopes and intercepts of the nine supercritical isotherms in Figure 3 obtained directly from the numerical tabulations of experimental data of the International Steam Tables [11] are collected in Table 1. These parameters can be used to estimate directly a critical temperature (Tc) and critical pressure (pc), respectively, and also to obtain the pressures and densities, of the percolation loci PB and PA. For densities both below PB, and densities above PA, on every isotherm, the departures in pressure p = (p‒pm)T, are found to be quadratic in density. A plot of density against the modulus |(p ‒ pm)|1/2 gives a straight line that interpolates at ∆p = 0 to obtain the percolation densities at PA and PB and, hence also the pressures using Equation (2), all as given in Table 1.
The present thermodynamic description of criticality has given rise to slightly different values for the critical constants than those previously reported in the case of argon [9] . The slopes of the mesophase rigidities decrease linearly with temperature in the vicinity of Tc, which is then obtainable from the experimental measurements of the rigidity constants in the mesoscale region by extrapolation of the slopes of the isotherms against temperature to zero (Figure 5). The present value obtained for Tc by this procedure (374.66) is slightly higher than previous literature values (given as 373.746˚C [11] ); here the uncertainties are too great to infer revised values.
Likewise, a critical pressure can then also be obtained from the supercritical isotherms by plotting the intercept of the linear plots (po in Equation (2)) against T ‒ Tc, and interpolating to T ‒ Tc = 0 (Figure 6).
The critical pressure we obtain by this procedure, pc = 221.7 ± 1 bar lies within the uncertainty of the literature results [11] , obtained from subcritical two-phase coexistence measurements (220.64 ± 0.03 bar). Nobody has ever measured the hypothetical “critical density” directly; ever since the critical temperature was discovered, experimentalists have used the law of rectilinear diameters (LRD) to obtain their “critical point” density [18] . This is well illustrated from the water liquid vapor coexistence densities in Figure 1. The lowest coexisting water mass density that can be measure is around 344 kg∙m−3 and the highest vapor mass density they can observe near Tc is 220 kg∙m−3 as seen in Figure 1. The mean of these two experimental liquid and vapor densities is 282 kg∙m−3. This is essentially the mean value obtained from experimental saturated vapor pressures in the coexistence region, and interpolation using the LRD, historically referred to as a “critical density” [18] .
Figure 4. Plots of the data points in the mesophase of nine supercritical isotherms taken numerically from the tables of Wagner and Kretzschmar [11] leading to the slopes and intercepts of Equation (2) to determine critical parameters without the assumption of a “critical point”; the temperatures and colour coding are the same as in Figure 3.
Figure 5. A value of the critical temperature as determined from slopes of the supercritical isotherms in the meso-phase region.
The coexisting gas and liquid densities at the critical temperature and pressure can also be conveniently and ac- curately obtained from the pressure-dependence of the supercritical percolation loci (Table 1). The percolation
Figure 6. Determination of a critical pressure value from the supercritical mesophase rigidity intercepts.
Table 1. Parameters in Equation (2) for supercritical mesophase isotherms p(ρ)T; the percolation loci are in units of density, kg∙m−3 and pressure inbar. The present critical parameters (bottom row in bold) correspond to rigidity slope Rm = 0.
densities in the range close to Tc are linear functions of pressure so that the coexisting densities can be obtained by plotting the percolation densities of gas (PB) and liquid (PA) against (p-pc) and interpolating to zero as seen in Figure 7. The uncertainties are quite large, but it is reassuring that the values obtained are not too different from the critical densities in Figure 1.
5. Phase Diagram
The data for the percolation locican now are used to construct a preliminary phase diagram of water and steam. Figure 8 shows the p-T projection that can be compared directly with the contours of properties in Figure 2. The immediate observation is that the loci of maxima the derived properties Cp, αp and κT lie broadly in the region of the supercritical mesophase bounded by the percolation loci.
The next observation from Figure 8 is that the critical point on the T, p plane is thermodynamically defined by an intersection of two percolation loci. All points on the Gibbs density surface must have a thermodynamic definition. The “critical point” hypothesized by van der waals, by contrast, has no thermodynamic definition; its
Figure 7. Determination of the densities of coexisting water (blue circles) and steam (red circles) at the critical temperature.
Figure 8. Phase diagram of water in the p-T plane; the coexisting density curves are taken from the experimental measurements of the IAPWS International Steam Tables [11] ; the supercritical percolation transition points PA (blue) and PB (red) intersect at Tc, and continue to define the metastable limit lines (usually referred to as spinodals) of the subcritical gas and liquid phases within the binodal region.
predicted existence was based upon a hypothesis regarding the form of the equation of state. Now, we find that two different equations of state are required for water and steam at all temperatures. Also plotted on Figure 8 are the experimental spinodals [19] [20] which bound the regions of metastable existence in the two-phase coexistence region at subcritical temperatures. Note also that the percolation transition loci cross at Tc and continue the below Tc to become the spinodals. This behavior was also observed for liquid argon [9] .
At Tc, PA and PB cross the critical coexistence line, to become subcritical limits of existence of the metastable compressed gas (p > psat) and expanded liquid phases (p < psat), respectively. The two percolation loci define the limits of existence of gas and liquid phases, not only above Tc, i.e. in the supercritical meso phase, but also below Tc, in the two-phase water-steam coexistence region. This is consistent with a phenomenological definition of PA and PB when liquid and gas have the same values of the rigidity (dp/dρ)T on the same isotherm whereupon (d2p/dρ2)T = 0 at both PA and PB, albeit at different pressures. At this point, there is also zero surface tension between water and steam, and consequently, within the mesophase, there is no barrier to spontaneous nucleation of steam from water (at PA) or water from steam (at PB).
None of the three supercritical maxima lines in Figure 2 coincide with PA or PB although the line of maximum κT on the p, T plane is quite close to PA. A better understanding of lines of maxima in these properties can perhaps be seen from the Gibbs density surface where the data points for PA and PB are plotted in Figure 9. When the various maxima in Cp. αp and κT, at constant temperature, as functions of density, are obtained from the tables [11] , and are put on the density phase diagram, a quite different picture emerges. All three maxima have their origins at the mean of the liquid and gas critical densities. The Cp maximum, which could be Bernal’s “hypercritical line” [12] essentially bisects the mesophase, at least up to 500˚C. Since Cp is associated with energy fluctuations, it could represent the colloidal mesophase inversion line when the dispersed phase changes from steam to water. Curiously, both αp and κT also stem from the central mean density at Tc, and both cease even to exhibit a maximum at all nearby the points at which they intersect the two percolations lines PA and PB, respectively.
At Tc, the rigidity difference between liquid and gas is zero, hence the surface tension should go to zero at a finite density difference [19] . This “critical divide” could be further understood by considering the surface tension. The percolation loci PA is the boundary of the existence of the liquid state for supercritical temperatures, it must connect up with the boundary for the non-existence of the liquid state for sub critical temperatures, i.e. the liquid-vapor decomposition spinodal. The spinodals are often defined operationally by the absence of a barrier to nucleation of the new phase, but an alternative definition is the point at which the surface tension of a liquid goes to zero as suggested by He and Attard [19] .
6. Discussion and Conclusions
In this preliminary investigation of supercritical water and steam, we have seen that the principle difference between liquid and gas is not just the density. Moreover the density difference does not disappear at the critical temperature. Rather, the structures of liquid and gas phases are fundamentally different in their description. Steam is a spatial distribution of small clusters of water molecules. Every species will have the same chemical
Figure 9. Equilibrium fluid phase diagram on the Gibbs density surface; the data points for the percolation loci are given in Table 1; loci of the maxima in heat capacity (Cp), isothermal compressibility (κT) and the thermal expansivity (αp) (red, blue and green dashed lines respectively) along the isotherms as functions of density, from thermodynamic data source [11] .
potential with monomers being the most probable, then dimers, trimers, etc. with ever decreasing probability, to balance the decreasing entropy with the increased enthalpy of association. These hydrogen bonded molecular clusters are occupied “sites” distributed in one large volume-spanning “hole”. Water, on the other hand is onelarge volume-spanning cluster, i.e. a network, of hydrogen bonded molecular “sites”, with a distribution within it of available “holes”. The foregoing analysis shows that this distinction between water and steam extends to supercritical temperatures.
It has been deduced from statistical thermodynamics [21] that the chemical potential is proportional to the probability of increasing the density by inserting one additional molecule into a “hole”. As a consequence of this relationship, the statistical properties of an average hole, relative to its environment of occupied sites and other holes, are the same as the statistical properties of the occupied site of an average molecule. We therefore expect to see a symmetry between water and steam in the work required to increase the density by simply adding one more occupied site in steam, or removing a hole, or part of a larger hole, in water by filling it with a water molecule, ensemble averaged. This is indeed seen in Figure 10 which shows a plot of the rigidity (dp/dρ)T i.e. the work required to increase the density at constant temperature.
The relative slope of the rigidity functions is the distinguishing thermodynamic property between gases and liquids. For steam it is seen to decrease quadratically with density, and for water it increases quadratically. This can be explained by the exact statistical mechanical relationship between the rigidity function, and fluctuations in the molecular number density (N) in a thermodynamically large fixed sub volume (V) of the equilibrium fluid. Infinite snapshots of such a dynamical system in statistical thermodynamics are a grand canonical ensemble. From the statistical properties of this ensemble, it is proven that the rigidity function is exactly related to the change in Gibbs chemical potential (μ) with number density (N) according to
 (3)
(3)
and from the thermodynamic theory of fluctuations [22] the right hand side is exactly and inversely proportional to an average dimensionless variance in N for a constant sub volume V, whereupon
 (4)
(4)
where R is the gas constant, T is the absolute temperature and V is a molar volume. For the ideal gas the variance in Equation (4) is 1, and it will approach zero for an amorphous ground state [7] as T ® 0 K. The rigidity can never be negative; it varies from zero at the critical temperature in the mesophase, to infinity for a metastable
Figure 10. Plot of (dp/dρ)T (rigidity) for the supercritical isotherm 400˚C obtained from the electronic steam tables of reference [11] showing a remarkable symmetry between steam and water, that can be explained by statistical fluctuations in density at the molecular level.
amorphous ground state. The symmetry seen in Figure 10 is then explained by the simple observation that fluctuations in N for the occupied molecular sites in the volume of gaseous state are mirrored in a corresponding liquid state. The distribution of “holes” in a liquid mirrors the distribution of “sites” in the gas. Number density fluctuations in the liquid state are determined by the fluctuations in the number of “holes”. The formal statistical theory of this translational invariance between insertion sites and holes for systems with continuous potentials was originally derived by Widom [21] .
In conclusion, the previous conjecture that the present description of liquid-gas criticality, already verified in the case of argon [9] , will be the same phenomenology for all liquids is here confirmed now for water and steam. The density difference between saturated water and steam does not go to zero at the critical temperature. Rather, above the critical temperature, the gas and liquid phases of water and steam are separated by a supercritical mesophase (regrettably referred to as steam II in a previous publication [8] ) which is a homogeneous mixture of gas-like small clusters, and liquid-like system spanning large clusters or microdroplets, all species with the same Gibbs chemical potential in thermal equilibrium. These phase boundaries are percolation transition loci and appear here either as very weak second-order or possibly third-order thermodynamic phase transition, referred to as percolation loci. These transitions are not well understood at the molecular theory level, but now require a more refined experimental and theoretical investigation.
Acknowledgements
We would like to thank the Scientific Committee of the 10th Asian Thermophysical Conference in South Korea Oct.1-5 2013 for the invitation to attend and present this paper. The presentation was well-received by the conference participants, with encouraging discussion and positive feedback. This manuscript was submitted to the International Journal of Thermophysics (IJTP) website in accord with ATPC guidelines for consideration by University of Korea Professor Jeong Won Kang as IJTP Editor of ATPC 2013 Proceedings, i.e. a member of the ATPC Scientific Technical Committee who invited the paper and attended the conference. On 29th Nov. 2013 I received E-mail from IJTP administrator Dr. D. Friend (of NIST, Boulder, USA), who had not attended ATPC-2013, and who was PRL reviewer A in a previous debate [23] . Dr. Friend procured two reports on this paper for the basis of this 2nd NS debate (APPENDIX 1).
We therefore also thank the Editors of Natural Science, who provide a valuable new forum for many areas of physical sciences, by publishing open debate with open access, where advancement of scientific ideas may have been impeded by prejudice and bigotry of the peer review processes in conventional journals, and in the IJTP case, by the absence of any appeal procedure.
References
- Glasser, L. (2004) Water, Water, Everywhere: Phase Diagrams of Ordinary Water Substance. Journal of Chemical Education, 81, 414-418. http://dx.doi.org/10.1021/ed081p414
- Guillot, B. (2002) A Reappraisal of What We Have Learned during Three Decades of Computer Simulations of Water. Journal of Chemical Education, 101, 219-260. http://dx.doi.org/10.1016/S0167-7322(02)00094-6
- Chaplin, M. (2013) Water Structure and Science. http://www.lsbu.ac.uk/water/
- Van der Waals, J.D. (1873) Over de Continuiteit van den Gas-en Vloeistoftoestand (On the Continuity of the Gas and Liquid State). Ph.D. Thesis, University of Leiden, Leiden.
- Binney, J.J., Dowrick, N.J., Fisher, A.J. and Newman, M.E.J. (1995) The Theory of Critical Phenomena: An Introduction to the Renormalization Group. Oxford Science Publications, Oxford.
- Wilson, K.G. and Nobel Lecture (1993) The Renormalization Group and Critical Phenomena. December 8 1982. In: Ekspång, G., Ed., Nobel Lectures, Physics 1981-1990, World Scientific Publishing Co., Singapore.
- Woodcock, L.V. (2012) Thermodynamic Description of Liquid State Limits. The Journal of Physical Chemistry B, 116, 3735-3744. http://dx.doi.org/10.1021/jp2116214
- Woodcock, L.V. (2013) Observations of a Liquid-Gas Critical Coexistence Line and Supercritical Mesophase Bounds from Percolation Transition Loci. Fluid Phase Equilibria, 351, 25-33. http://dx.doi.org/10.1016/j.fluid.2012.08.029
- Woodcock, L.V. (2013) Gibbs Density Surface of Fluid Argon: Revised Critical Parameters. International Journal of Thermophysics, 34, 1411-1416.
- Gibbs, J.W. (1873) A Method of Representation of the Thermodynamic Properties of Substances by Means of Surfaces. In: Collected Works of J. Willard Gibbs, Longmans Green and Co, New York, 1928, Chapter 1: Original Publication: Trans. Conn. Acad. Arts Sci., 2, 382.
- Wagner, W. and Kretzschmar, H.-J. (2008) IAPWS- IF’97 International Steam Tables: Properties of Water and Steam. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-540-74234-0
- Bernal, J.D. (1964) The Bakerian Lecture 1962, The Structure of Liquids. Proceedings of the Royal Society (London) A 280, 299-322. http://dx.doi.org/10.1098/rspa.1964.0147
- Widom, B.J. (1972) Phase Transitions and Critical Phenomena. In: Domb, C. and Green, M.S., Eds., Phase Transitions and Critical Phenomena, Vol. 2, Academic Press, Waltham.
- Brazhkin, V.V., Fomin, Y.-D., Lyapin, A.G., Ryzhov, V.N. and Tsiok, E.N. (2011) Widom line for the Liquid-Gas Transition in Lennard-Jones System. The Journal of Physical Chemistry B, 115, 14112-14115. http://dx.doi.org/10.1021/jp2039898
- Simeoni, G.G., Bryk, T., Gorelli, F.A., Krisch, M., Ruocco, G., Santoro, M. and Scopigno, T. (2010) The Widom Line as the Crossover between Liquid-Like and Gas-Like Behaviour in Supercritical Fluids. Nature Physics, 6, 503-507. http://dx.doi.org/10.1038/nphys1683
- Brazhkin, V.V., Fomin, Yu.D., Lyapin, A.G., Ryzhov, V.N. and Trachenko, K. (2012) Two Liquid States of Matter: A Dynamic line on a Phase Diagram. Physical Review E, 85, 031203. http://dx.doi.org/10.1103/PhysRevE.85.031203
- Gopal, E.S.R. (2000) Critical Opalescence. Resonance, 5, 37-45. This prevailing explanation of critical opalescence as reviewed by Gopal requires molecular fluctuations or Brownian motion, according to the theories of Einstein and Smoluchowski. It now seems likely that the effect may have little to do with molecular level fluctuations directly, and that there is a simpler explanation as Tyndall scattering which occursdue to the colloidal dispersion nature of the mesophase. http://www.chm.bris.ac.uk/webprojects2002/pdavies/Tyndall.html
- Reif-Acherman, S. (2003) History of the Law of Rectilinear Diameters. Quimica Nova, 33, 2003-2013.
- He, S.N. and Attard, P. (2005) Surface Tension of a Lennard-Jones Liquid under Supersaturation. Physical Chemistry Chemical Physics, 7, 2928-2935. http://dx.doi.org/10.1039/b507106b
- Shamsundar, N. and Lienhard, J.H. (1993) Equations of State and Spinodal Lines―A Review. Nuclear Engineering and Design, 141, 269-287.
- Widom, B.J. (1963) Some Topics in the Theory of Liquids. The Journal of Chemical Physics, 39, 2808. http://dx.doi.org/10.1063/1.1734110
- Landau, L.D. and Lifshitz, E.M. (1958) Statistical Physics. Pergamon, London.
- Woodcock, L.V. (2013) Fluid Phases of Argon: A Debate on the Absence of van der Waals’ Critical Point. Natural Science, 5, 194-206. http://dx.doi.org/10.4236/ns.2013.52030
Appendix 1
Reviews of manuscript “Gibbs density surface of water and steam”:
submitted (28-9-13) International Journal of Thermophysics:
reviewing Editor: Dr. D. Friend (NIST: Boulder CO)
Reviewer 1: (Prof. J. V. Sengers, University of Maryland wrote:)
This is a revolutionary paper challenging both the famous principle of Van der Waals concerning the continuity of the gaseous and liquid state and the modern theory of critical phenomena in terms of renormalization-theory and critical-point universality as applied to the vapor-liquid critical point in fluids. Basically, this paper resurrects an old picture in terms of liquidons and gasons, reviewed by Levelt Sengers [1] , but now in terms of percolation theory. I want to emphasize that I greatly admire the depth of knowledge of the author on the subject of Gibbsian thermodynamics. Nevertheless, after thinking about it, I find the evidence presented not convincing.
First, I object to using the IAPWS-97 Industrial Formulation for the Thermodynamic Properties of Water and Steam [Ref. 11 in manuscript] to draw any conclusions about the thermodynamic critical behavior of water and steam. All figures appear to be based on IAPWS-97. However, IAPWS-97 is an industrial formulation developed for high computational speeds, but this equation does not even claim to be qualitatively reliable in the critical region. For example, from Figure 1, based on IAPWS-97, one cannot make any reliable conclusion about the behavior of the coexisting vapor and liquid densities near the critical point and whether there exists or does not exist a gap near the critical point. A better equation would be the IAPWS-95 Formulation for the Thermodynamic Properties of Water and Steam [2] , but even that one fails to give a proper account of some thermodynamic properties of water and steam in the near vicinity of the critical point.
My second problem, which is a more fundamental one and which also pertains to a previous article of the author [Ref. 9 in manuscript], is that the author completely ignores the experimental evidence in support of critical-point universality and of the resulting critical behavior of thermodynamic properties in terms of critical power laws [3] . For instance, the isochoric heat capacity has been shown to diverge at the vapor-liquid critical point [4] -[6] . The most recent experiment concerning the behavior of the isochoric heat capacity of a fluid near the vapor-liquid critical point is the one reported by Haupt and Straub [7] . They found that CV diverges with a critical exponent α = 0.1105 ± 0.027 in excellent agreement with the theoretical value α = 0.110 ± 0.003 for Ising-like systems [8] . Unfortunately, the author is silent about the critical behavior of CV. The author claims in a previous publication [Ref. 9 in manuscript] that his theory is in agreement with the experimentally observed thermodynamic behavior of argon in the critical region. However, I have not found any comparison in that paper with the experimental data for the isochoric heat capacity of argon in the critical region [4] -[6] .
As long as the author cannot demonstrate that his theory implies a similar divergence of CV as observed experimentally, I do not think that the manuscript should be accepted for publication.
References
- Levelt Sengers, J.M.H. (1979) Liquidons and Gasons; Controversies about the Continuity of States. Physica A: Statistical Mechanics and Its Applications, 98, 363-402. http://dx.doi.org/10.1016/0378-4371(79)90145-6
- Wagner, W. and Pruß, A. (2002) The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. Journal of Physical and Chemical Reference Data, 31, 387. http://dx.doi.org/10.1063/1.1461829
- Sengers, J.V. and Shanks, J.G. (2009) Experimental Critical-Exponent Values for Fluids. Journal of Statistical Physics, 137, 857-877. http://dx.doi.org/10.1007/s10955-009-9840-z
- Bagataskii, M.J., Voronel, A.V. and Gusak, V.G. (1963) Soviet Physics, JETP, 16, 517.
- Anisimov, M.A., Voronel, A.V. and Gorodetskii, E.E. (1971) Soviet Physics, JETP, 33, 605.
- Voronel, A.V., Borgunova, V.G., Smirnov, V. A., Shmakov, N.G. and Shcheochikhina, V.V. (1973) Soviet Physics, JETP, 36, 505.
- Haupt, A. and Straub, J. (1999) Evaluation of the Isochoric Heat Capacity Measurements at the Critical Isochore of SF6 Performed during the German Spacelab Mission D-2. Physical Review E, 59, 1795-1802. http://dx.doi.org/10.1103/PhysRevE.59.1795
- Pelisso, A. and Vicari, E. (2002) Critical Phenomena and Renormalization-Group Theory. Physics Reports, 368, 549- 727. http://dx.doi.org/10.1016/S0370-1573(02)00219-3
Reviewer 2
This manuscript proposes a major reinterpretation of the fluid region phase diagram of water, and presumably all simple fluid systems. Significantly, there is no critical point in this new description. The vapor and liquid states extend above the critical temperature, bounding a supercritical “mesophase” with colloid-like characteristics. This alternative view of the phase diagram is supported quite convincingly by the figures presented in the manuscript, and does appear to offer a plausible alternative explanation to the usual one involving the critical point which could explain a number of unresolved experimental observations (well summarized in the introduction of the manuscript). Which one is correct still needs to be established, presumably by further experiments and maybe theory. It is important that this new perspective is presented to the scientific community so that it will spur on such investigations. I support publication of the manuscript, which is well written.
Reviewer 3 (Dr. D. Friend NIST Communicated)
While challenges to conventional interpretations of physical phenomena are certainly worth considering, their threshold for publication must be set reasonably high in terms of an ability to interpret experimental results, predict new phenomena, or simplify our understanding of the physical system. This paper challenges about 150 years of theory and experiment, and offers very little in return.
The premise of the approach seems to stem from an interpretation of Figure 1. Evidently lack of convergence of an EOS (IAWPS IF97) is interpreted as a signal for an onset of a percolation transition. No experimental evidence is given for this! It seems clear that other EOS models could have convergence issues in at other state points, or not at all. For instance, a critical region EOS (e.g., a scaling model or other RG model, a simple interpolation model, etc.) might show no termination of the saturation lines other than at the conventional critical point. While this observation may not negate the entirety of the current manuscript, it points to a significant flaw. In the first full paragraph of p. 3, it is stated that the “5-figure precision density data” indicates that Wilson's critical point “does not accord with experiment.” No experimental evidence is given―only results from an EOS, which, by construction conforms to some model behavior and some sets of data.
Similarly the statement that there is “no universality” contradicts most evidence (whatever “spans the dimensions” might mean). The statement about the mesophase above Tc is also given without evidence.
I can see no reason to re-fit tabulated EOS results to get new liquid and vapor saturation lines. (Evidently experimental data were again not considered.) The equations (in Figure 1) contradict most interpretations of experimental behavior in the critical region (e.g. symmetry and critical exponents). The equations are given without uncertainties, comparisons to other saturation lines, or comparisons to data.
Figure 2 is again an observation from a particular EOS: these common plots are not often considered “somewhat of a mystery,” but are consistent with equation of state models that incorporate a critical point. The behavior of dp/drho|T would be the same with and without the conventional critical point, so not much is added in this discussion.
While “hole” models of fluids have been published in numerous papers, the lack of experimental evidence or predictive powers have limited there utility: nothing changes in the current version. As noted, there is “no such well-defined distance to define PA and PB.” The argument about a “steep [??] hydrogen bond” seems irrelevant for a model that is supposed to be common for other (all?) fluids: presumable this argument was not used for argon, and such ad hoc explanations do not replace the universality of critical phenomena. On p. 5, lines 43 - 44, it is not clear what is meant by “change in dp/drho|T” and no precise definition is given.
Figure 3 is not at all clear. Firstly, the caption citation to Ref. 5 seems wrong, but the previously cited “International Steam Tables” is not an experimental source: these are not “experimental data points.” There is no explanation of why portions of the isotherms are assumed to have constant slopes, nor why the transitions lines are assumed to be at constant density in Figure 3 but not in Figure 4. Were fits in Figure 4 really made to only tabulated densities from an EOS, and the absence of multiple values interpreted to give constant slopes? Do actual data provide evidence for these constant slopes―and to what uncertainty?
The conjecture of linearity in the mesophase seems to be made without experimental support. The discussion of clusters is made without experimental support. The spontaneous coalescence is described without experimental support. The critical opalescence has been explained in a conventional critical region theory―what is added here?
The calculations of Table 1 are not well described. Such tables without uncertainty estimates convey very little information. (Give evidence that things are linear “within bounds of uncertainty.”) Why restrict yourself to “numerical tabulations” in Ref. [11] . These are not experimental data, and are not even representative of the “best” EOS models. Why not use the equations themselves, rather than tables, to evaluate derivatives?
In summary, particle-hole theories can be useful in statistical models (such as lattice models), but they seem very limited for interpreting existing experimental data. This paper presents nothing that contradicts existing approaches to criticality, and provides no experimental based evidence for the model under consideration. There seems to be no reason to adjust the critical values of water, nor reject the concept of critical behavior.
Author Response to Reviewers
Sengers: “This is a revolutionary paper challenging both the famous principle of Van der Waals concerning the continuity of the gaseous and liquid state and the modern theory of critical phenomena in terms of renormalization-theory and critical-point universality as applied to the vapor-liquid critical point in fluids.”
Author: In fact this particular manuscript on water and steam is not so “revolutionary”. There are already several (5+ pipeline) refereed and published papers of this new science of criticality with all the supporting evidence, including references [7] - [9] in this manuscript, that Sengers has not properly taken into account. The first of these papers, which is reference 7 of my manuscript, titled “Thermodynamic description of liquid state limits” was published in J. Phys. Chem. (B) two years ago.
Sengers: “Basically, this paper resurrects an old picture in terms of liquidons and gasons, reviewed by Levelt Sengers [1] , but now in terms of percolation theory.
Author: This hitherto obscure historical review by Levelt-Sengers, is interesting, and indeed very relevant, but it is not an objective review of the science. It is politically prejudiced throughout, and highly subjective in its conclusions, especially in favour of the Dutch school and van der Waals hypothesis. The Levelt-Sengers review, interestingly, reveals the names of several early scientists expressed alternative descriptions or reservations of the van der Waals “continuity of liquid and gas” hypothesis; including Faraday, Mendeleev, Ramsay, Gouy, Mathias and Cailletet.
For Sengers to describe the new science of liquid-gas criticality and the supercritical mesophase as a “resurrection” of this nebulous early nineteenth-century idea is quite a stretch. There is no definition of “liquidons and gasons”; and didn’t even know this paper existed until he sent it to me by e-mail last September.
Sengers: “First, I object to using the IAPWS-97 Industrial Formulation for the Thermodynamic Properties of Water and Steam [Ref. 11 in manuscript] to draw any conclusions about the thermodynamic critical behavior of water and steam. All figures appear to be based on IAPWS-97. However, IAPWS-97 is an industrial formulation developed for high computational speeds, but this equation does not even claim to be qualitatively reliable in the critical region. For example, from Figure 1, based on IAPWS-97, one cannot make any reliable conclusion about the behavior of the coexisting vapor and liquid densities near the critical point and whether there exists or does not exist a gap near the critical point. A better equation would be the IAPWS-95 Formulation for the Thermodynamic Properties of Water and Steam [2] , but even that one fails to give a proper account of some thermodynamic properties of water and steam in the near vicinity of the critical point.”
Author: Use of IAPWS-95 rather than-97may improve the precision, but would not change the science. However, I do agree with Sengers that both the IAPWS-97 formulation of Properties of Water and Steam (which I use), and also the IAPWS-95 formulation, cannot be accurate in the immediate vicinity of the critical temperature. What Sengers fails to recognize, however, is the reason for the inadequacy of these modern steam tables in the vicinity of Tc. It is precisely because the functional forms used for the parameterization of the data, in both IAPWS-95 and IAPWS-97 wrongly assume the LRD in conjunction with existence of a critical point singularity on the Gibbs density surface, that is the cause of the inadequacy. This interesting point can be included. Indeed, it is a good reason for publication since the new science explains the root of the problem!
Sengers: My second problem, which is a more fundamental one and which also pertains to a previous article of the author [Ref. 9 in manuscript], is that the author completely ignores the experimental evidence in support of critical-point universality and of the resulting critical behavior of thermodynamic properties in terms of critical power laws [3] .
Author: Non-universality is discussed in references [7] and [8] of my manuscript. Sengers cites his own paper in 2009 with a former research student (Shanks PhD Maryland 1986) as being in support of “critical-point universality”. Reference [3] of Sengers list in fact does not contain any new experimental data that is relevant to my manuscript on water and steam or indeed to liquid-gas criticality. Citing 254 references the paper is actually a belated publication of mainly review Chapters in the PhD Thesis of his former student Shanks (Reference 221, Shanks, PhD Thesis 1986) and some experiments on a binary liquid. This is published as part of Conference Proceedings 25 years after experiments on the binary liquid were actually conducted. This review by Sengers and his former student therefore is of marginal or no relevance to the present manuscript.
Sengers: “For instance, the isochoric heat capacity has been shown to diverge at the vapor-liquid critical point [4] - [6] .
Author: It is rather unusual to go back 50 years to dig out these three papers. On looking through them, it is clear this cannot be “reproducible experimental evidence”. This perhaps explains the 40-year gap.
Both Sengers and Voronel appear to have been under a life-long misapprehension regarding the divergence of the state function Cv = (dU/dT)V, where U is the internal energy. This property depends only upon energy fluctuations, and, unlike Cp and KT, which depend on density fluctuations, for gas-liquid equilibria, Cv does not diverge at the critical temperature. This misapprehension appears to have prejudiced the design, the measurement procedures, and the interpretation of the experimental results.
The paper by Haupt and Strabe (Sengers ref [7] ) also appears to be yet another, of many in the literature (on different aspects of criticality) whose results and conclusions have been adversely prejudiced by the assumption of the existence of a “critical point” singularity at the outset of the design of the experiment, through choice of the experimental measurements, and the final interpretation of their results. It is hard to understand how these physicists could have all been under a basic misapprehension about the behavior of Cv(T) along any isochore in a liquid gas system. Even the hypothetical van der Waals “critical point”, for a real gas-liquid system, could not have such divergence of Cv.
Sengers: The most recent experiment concerning the behavior of the isochoric heat capacity of a fluid near the vapor-liquid critical point is the one reported by Haupt and Straub [7] . They found that CV diverges with a critical exponent α = 0.1105 ± 0.027 in excellent agreement with the theoretical value α = 0.110 ± 0.003 for Ising-like systems [8] ”.
Author: The experiment referred to here is a rather obscure one-off experiment on SF6 aboard the space shuttle, and is not easily verifiable or reproducible. Again, I must say that I find it hard to understand how these authors “found” a divergence in a property (Cv) that does not, and could not, diverge at any point on its Gibbs T-density surface of liquid-gas equilibria. Moreover, Cv would not diverge at the critical temperature even in the van der Waals hypothesis of a singular critical density were true. It is only those properties that depend on a divergence of density fluctuations, arising from the thermodynamic condition (dp/dV)T ® 0 that diverge, e.g. isothermal compressibility or isobaric heat capacity. All isochoric reversible processes on Gibbs T-density surface, e.g. (dU/dT)v (= Cv) are continuous without divergences, basically because there is no latent heat associated with expansion in reversible isochoric processes.
Any comparison, or coincidence, between whatever it is that these authors actually measured, and the published value of an exponent for Ising models is therefore not relevant. There is certainly no valid reason for rejection. Quite the opposite, there is now an overwhelming case to open up this debate.
Sengers: Unfortunately, the author is silent about the critical behavior of CV. The author claims in a previous publication [Ref. 9 in manuscript] that his theory is in agreement with the experimentally observed thermodynamic behavior of argon in the critical region. However, I have not found any comparison in that paper with the experimental data for the isochoric heat capacity of argon in the critical region [4] - [6] .
Author: Reason for the “silence” is that there isn’t much of interest to say about Cv; unlike Cp there is no divergence. Along any isochore that traverses within the two-phase region at TcCv is everywhere well-behaved. The science of liquid-gas criticality regarding Cv is as follows.
For all temperatures below Tc, the thermodynamic state function Cv = (dU/dT)v where U is the internal energy is the mean of heat capacities of coexisting liquid per mole of liquid and of the gas per mole of gas as given by the Lever rule of apportionment. At the critical temperature this reaches a maximum value but, unlike the heat capacity at constant pressure (Cp), or the isothermal compressibility, Cv does not diverge to infinity. For T > Tc, along any isochore, Cv decreases monotonically from its maximum value at Tc. There is no discontinuity in Cv at Tc with any similarity to the singularities observed in Ising lattice gases. In this respect, Cv is a rather uninteresting property of a thermodynamic liquid-gas system. Lattice gases are not thermodynamic systems in the Gibbs definition, i.e. of being able to change energy by reversible exchange of both heat and work, because of the configurational constraints, they can exhibit energy fluctuations that behave quite differently.
Sengers: As long as the author cannot demonstrate that his theory implies a similar divergence of CV as observed experimentally, I do not think that the manuscript should be accepted for publication.
Author: Sengers doesn’t seem to understand that there is no new “theory” here. What has been proposed is an alternative phenomenological description of the thermodynamic phase limits of liquids and gases on the Gibbs density surface that is consistent with Gibbs phase rule, and not based upon any hypothesis (such as van der Waals) or various other ideas involving mean-field theories and universality.
What can be demonstrated is the invalidity of Sengers principle reason for rejection using literature experimental data for the isochoric heat capacity of water and steam (see graph below). The literature value of Tc for water is 373.95˚C ± 0.02˚C. On the plot below is given the Cv values for the near-critical/supercritical isotherm (small black circles) 374.00˚C (i.e. Kelvin T/Tc = 1.0001), alongside the two values for saturated steam (red circle) and saturated water (blue circle) in coexistence at the subcritical 2-phase region temperature of 373.80˚ (T/Tc = 0.9996). There is no divergence of Cv!
Figure A1. The heat capacity at constant volume (Cv) as a function of density for the supercritical isotherm (374.0˚C) of steam and water within 0.1 K of the critical temperature (Tc = 373.9˚C) i.e. T/Tc ~ 1.0001; the values of Cv at coexistence T/Tc ~ 0.9999 are also shown; the data is from reference [11] in the paper.
By contrast, the values of Cp, which does diverge at Tc, for steam and water at 373.8˚C are 51,520 J/(molK) and 37,000 J/(molK) respectively, i.e. of the Order 1000 times Cv!
Friend: “While challenges to conventional interpretations of physical phenomena are certainly worth considering, their threshold for publication must be set reasonably high in terms of an ability to interpret experimental results, predict new phenomena, or simplify our understanding of the physical system. This paper challenges about 150 years of theory and experiment, and offers very little in return.”
Author: The paper that first challenged “150 years of theory and experiment”, reference [7] in the manuscript was actually published 2 years ago. Here is a paragraph from those conclusions: Quote: “Thus, we reach the remarkable conclusion that a liquid-gas critical point, as hypothesized and parameterized by van der Waals 2 and accepted by the physics community for 140 years 4,23−27, does not exist as such. There is no universality of critical phenomena that spans the dimensions. 4,32 Rather, in the V(T, p) surface, we find a line of uniform chemical potential at the critical temperature and pressure, above which there exists a supercritical meso-phase bounded by the second-order percolation transitions, and below which there is the familiar liquid-vapor coexistence region”.
What this manuscript “offers in return” is a vindication of that early conclusion which was based upon percolation transitions in model hard-sphere and square-well model systems. Here we now see, the conclusion is entirely consistent with all known thermodynamic properties of water and steam.
Friend: “The premise of the approach seems to stem from an interpretation of Figure 1. Evidently lack of convergence of an EOS (IAWPS IF97) is interpreted as a signal for an onset of a percolation transition. No experimental evidence is given for this! It seems clear that other EOS models could have convergence issues in at other state points, or not at all. For instance, a critical region EOS (e.g., a scaling model or other RG model, a simple interpolation model, etc.) might show no termination of the saturation lines other than at the conventional critical point. While this observation may not negate the entirety of the current manuscript, it points to a significant flaw.”
Author: The IAWPS-97 water steam tables are themselves the “experimental evidence” in this case. Here is some more experimental evidence, with a simple question for Friend? Take a look at all the raw experimental data in Figure 2 of Guggenheims 1945 classic paper on corresponding states (JCP v.13) where nothing has been “fitted”.
Figure A2. Guggenheim’s (1947) reduced plot of temperature (T/Tc) as a function of reduced density (ρ/ρc) of then available experimental data points for the coexisting densities up to the critical temperature (T/Tc = 1): the reason for the missing data points in the near-critical region of the parabola between the maximum attainable gas density and the minimum attainable liquid density at 2-phase coexistence is a horizontal straight line dividing subcritical 2-phase coexistence and a supercritical mesophase.
Why are there no experimental density data for saturated gas density between ρ/ρc = 0.8 and 1.0? Why are there no liquid state density points between ρ/ρc =1.0 and 1.2? Is this not the ultimate simple experimental evidence?
Friend: In the first full paragraph of p. 3, it is stated that the “5-figure precision density data” indicates that Wilson’s critical point “does not accord with experiment.” No experimental evidence is given―only results from an EOS, which, by construction conforms to some model behavior and some sets of data.
Author: Figure 2 of my paper is the experimental evidence! The source of data plotted is an accurate parameterization of experimental data to within 0.9999 of T/Tc (i.e. 0.1 K). Use of original experimental data points rather than IAPWS-97 parameterization, which is not model-based) would give exactly the same graph.
Friend: Similarly the statement that there is “no universality” contradicts most evidence (whatever “spans the dimensions” might mean).
Author: The statement “no universality” indeed contradicts many theoretical physicists publications on the subject, but theory is not “evidence”. The statement does not contradict the experimental thermodynamic property investigations of liquid-gas equilibria and liquid-gas criticality going back 150 years to the first measurements on CO2 by Andrews.
“Spanning the dimensions” refers to a widely held misapprehension that has arisen from the exact solution for a partition function showing a similar critical singularity in 1, 2 and 3 dimensions. (see: M. Kac, G.E. Uhlenbeck and J. Hammer “On the van der Waals theory of the vapor-liquid equilibrium” (I) J., Math. Phys., 4 216 (1963) (II) ibid 4 2239 (1963) (III) ibid 5 60 (1964).) for Kac-van der Waals mean-field model (reference 32 in reference 7 of my manuscript). The Kac model is a state (temperature)-dependent effective pair potential, and as such, it does not correspond to any model molecular Hamiltonian and is therefore inapplicable to real molecules that comprise Gibbs thermodynamic systems. The Kac model effective-pair potential artifact has no real molecular counterpart, and is not applicable to real molecular liquid-gas thermodynamic equilibria.
Friend: The statement about the mesophase above Tc is also given without evidence.
Author: The nature of the mesophase is evidenced in references [7] -[9] .
Friend: I can see no reason to re-fit tabulated EOS results to get new liquid and vapor saturation lines. (Evidently experimental data were again not considered.) The equations (in Figure 1) contradict most intepretations of experimental behavior in the critical region (e.g. symmetry and critical exponents). The equations are given without uncertainties, comparisons to other saturation lines, or comparisons to data.
Author: Yes, of course they contradict most interpretations etc…that’s precisely the point of my manuscript. I’ll repeat it again: the thermodynamic equilibrium data for water-steam system is inconsistent with previous interpretations based upon van der Waals hypothesis, and entirely consistent with two-phase coexistence up to a critical dividing line with a 20% density gap at Tc.
Friend: Figure 2 is again an observation from a particular EOS: these common plots are not often considered “somewhat of a mystery,” but are consistent with equation of state models that incorporate a critical point. The behavior of (dp/dρ)T would be the same with and without the conventional critical point, so not much is added in this discussion.
Author: The behavior of (dp/dρ)T would be quite similar with and without the conventional critical point, but definitely not “the same”. All we are showing here is that the data for water and steam is entirely consistent with the existence of the supercritical mesophase in which, over a wide range of density, (d2p/dρ2)T = 0 to within the 5-figure precision uncertainty.
Friend: While “hole” models of fluids have been published in numerous papers, the lack of experimental evidence or predictive powers have limited there utility: nothing changes in the current version. As noted, there is “no such well-defined distance to define PA and PB.” The argument about a “steep [??] hydrogen bond” seems irrelevant for a model that is supposed to be common for other (all?) fluids: presumable this argument was not used for argon, and such ad hoc explanations do not replace the universality of critical phenomena.
Author: This manuscript has nothing to do with the “hole models” referred to.
The “hole volume” in the liquid state referred to in this manuscript is not a “model”; it is actually a thermodynamic state function chemical potential exp (−μ/kT) = Vhole/V
where Vhole/V is a normalized probability of inserting the additional molecule anywhere which implies “holes”-but there is no “molecular model”. Presumption of “the universality of critical phenomena” is evidence of prejudice.
Friend: On p. 5, lines 43 - 44, it is not clear what is meant by “change in (dp/dρ)T” and no precise definition is given.
Author: Change in rigidity (dp/dρ)T with density are of course manifested in the second derivative (d2p/dρ2)T. The following changes or inequalities define the percolation loci thermodynamically along any isotherm
Friend: There is no explanation of why portions of the isotherms are assumed to have constant slopes, nor why the transitions lines are assumed to be at constant density in Figure 3 but not in Figure 4. Were fits in Figure 4 really made to only tabulated densities from an EOS, and the absence of multiple values interpreted to give constant slopes? Do actual data provide evidence for these constant slopes-and to what uncertainty?
Author: The constant slopes is not an assumption; the data points, when plotted on an EXCEL sheet, give linear trendlines with a regression coefficient of 0.999…etc. with remarkable consistency in the mesophase for every model system or real liquid that we have looked at, including the present water-steam.PA and PB in Figure 3 were originally schematic. The values obtained in Figure 4 show that PB decreases slightly with density as T increases T > Tc.
Reviewer 3: The conjecture of linearity in the mesophase seems to be made without experimental support.
Author: The linearity is found in all the model square-well model fluids, from sticky spheres to mean field limit, in all Lennard-Jones fluids, in liquid argon, and now, here, in water-steam. It is not a conjecture. It is an experimental observation!
Friend: The discussion of clusters is made without experimental support. The spontaneous coalescence is described without experimental support.
Author: Whilst presently there is not yet real experimental verification of the detailed nature of the clustering at the molecular level, computer simulations in reference 8 and 9 of the manuscript, and also in another recently published paper (D. M. Heyes and L. V. Woodcock , “Critical and Supercritical Properties of Lennar-Jones Fluids” Fluid Phase Equilibria 356 351 - 308 (2013) show that the distribution of clusters in the mesophase, when a cluster is defined by a distance of maximum attractive force, is bi-modal. There are system-spanning liquid clusters or Order N, and small gas clusters of Order 1 to n (where n is a small number Order 10).
Friend: The critical opalescence has been explained in a conventional critical region theory--what is added here?
Author: van der Waaals hypothesis of the supercritical region around the mean critical density as a homogeneous fluid, the only possible origin of fluctuations that could give rise to light scattering is molecular Brownian motion as described by Einstein 100 years ago and later Smoluchowsky. What is suggested here is an alternative and more plausible explanation based on the colloidal nature of the mesophase. All otherwise transparent colloidal systems, e.g. clouds or foams, scatter white light when one phase is dispersed with droplets of a different refractive index to the continuous phase. It is called Tyndall scattering.
Friend: The calculations of Table 1 are not well described. Such tables without uncertainty estimates convey very little information. (Give evidence that things are linear “within bounds of uncertainty”.) Why restrict yourself to “numerical tabulations” in Ref. 11. These are not experimental data, and are not even representative of the “best” EOS models. Why not use the equations themselves, rather than tables, to evaluate derivatives?
Author: Yes, I agree here. The paper could be improved if I use the equations rather than the tabulations and indeed also evaluate the derivatives if at all possible. I could do this to improve the paper, and also the precision of PB and PA in the Figures, but it will not change any fundamental conclusions.
Friend: In summary, particle-hole theories can be useful in statistical models (such as lattice models), but they seem very limited for interpreting existing experimental data.
Author: I don’t disagree with this statement. This manuscript, however, is not about particle-hole model theories.
Friend: This paper presents nothing that contradicts existing approaches to criticality, and provides no experimental based evidence for the model under consideration.
Author: There is no “model” under consideration. It is exactly the opposite, all thermodynamic data used in this manuscript is extracted from precise numerical parameterization of validated literature experimental thermodynamic properties of water and steam. This original thermodynamic data is entirely consistent with the non-existence of a “critical point” on the Gibbs density surface.
Friend: There seems to be no reason to adjust the critical values of water, nor reject the concept of critical behavior.
Author: Except for “the critical density”, which does not exist, I agree that the data used here in the water- steam supercritical mesophase needs sharpening up before an accurate (5-figure) revision may be possible. This preliminary manuscript however, now consolidates the many compelling reasons, to abandon the concept of a van der Waals critical singularity, and brings new insight into the supercritical region between gas and liquid state limits.

















