Natural Science
Vol.6 No.7(2014), Article ID:45341,8 pages DOI:10.4236/ns.2014.67047
Entropy and Entanglement of Moving Two Atoms in a Squeezed Field via Four-Photon Process
Sayed Abdel-Khalek1,2*, Saraa Hussein Halawani2
1Mathematics Department, Faculty of Science, Sohag University, Sohag, Egypt
2Mathematics Department, Faculty of Science, Taif University, Taif, Saudi Arabia
Email: *sayedquantum@yahoo.co.uk, mabdel_k@ictp.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 19 December 2013; revised 19 January 2014; accepted 26 January 2014
ABSTRACT
In this paper, the entanglement between two atoms and squeezed field via four photon process is investigated. The dynamical behavior of the entanglement between two atoms and a squeezed field is analyzed. In particular, the effects of the atomic motion, the initial atomic state and the field squeezing are examined. A high amount of entanglement is generated by increasing the field squeezing. Furthermore, we show that a sudden death and sudden birth emerge when the moving atoms are initially prepared in the excited state.
Keywords:Von Neumann Entropy, Entanglement Sudden Death and Sudden Birth, Squeezed State

1. Introduction
In recent years, the studies focus on the quantum entanglement concept or so called non-local correlation [1] -[14] , which play an important role in quantum information theory, quantum computation and communication [15] [16] , quantum cryptography [17] -[19] , quantum teleportation [20] , and dense coding [21] [22] . Also, there is a lot of attention has been focused on information entropies as a measure of entanglement in quantum information such as von Neumann entropy (NE) [12] , Linear entropy (LE), Shannon information entropy (SE) [23] and atomic Wehrl entropy (AWE) [4] [24] . The atomic Wehrl entropy had been introduced and applied to the Jaynes-Cummings model and its relation to the von Neumann entropy had been obtained in [5] , all these measures to test whether a given quantum state is separable or entangled. Some physical phenomenons are observed as a result of entanglement measure such as “entanglement sudden death” (ESD) and “entanglement sudden birth” (ESB) [6] [25] is the creation of entanglement where the initial unentangled qubits can be entangled after a finite evolution time. The coherent field is a kind of the electromagnetic field which have a minimum-uncertainty and it’s more classical field than it’s quantum field [7] . Other states of the electromagnetic field, such as squeezed states, even and odd coherent states and so on, don’t have minimum-uncertainty and they are nonclassical states, and have more applications for quantum communications and weak signal detection [8] .
Quantum and classical correlations are at the heart of quantum information theory. It is seen a great deal of attention pointed to a subtler but more general kind of quantum correlations. In this regard, there are different entanglement measures and quantifiers have been used for the pure and mixed states such as concurrence [26] [27] , quantum discord [28] and Fisher information [29] -[31]
Recently, much attention has been focused on the properties of the Tavis-Cummings model (TCM) when the time dependent coupling with field is considered. The entanglement between two atoms (qubits) is discussed in the case of open and closed quantum system [32] [33] . Also, the entanglement of two moving atoms interacting with a single-mode field via a three-photon process is investigated [9] . In [3] , the authors studied the atomic Wehrl entropy of a V-type three-level atom interacting with two-mode squeezed vacuum state and the results show that the atomic motion and the mode structure play important roles in the evolution of the atomic Wehrl entropy. In our investigation, we focus the study of the entanglement between moving and non moving two two-level identical atoms interacting with a strong squeezed field via four-photon process in a closed system and our main aim is looking for some important phenomenons that accessiable appearance in the interaction such as entanglement sudden death (ESD) and entanglement sudden birth (ESB) for the system under consideration, and examine the effects of the atomic motion parameters p₁ and p₂, the atomic position θ and squeeze parameter r on the interaction system and we want to be convinced that “Are these parameters have a real effect on the interaction system?”
The paper is prepared in the following order: In Section 2, the Hamiltonian system and the solution for the system under consideration will be given. In Section 3, we introduce the von Neumann entropy measure and discussed the results. The main conclusion is summarized in Section 4.
2. The Model
We consider two identical atoms moving in a cavity of length L, and they have the same velocity i.e. 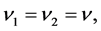 and interacting with a strong squeezed field via four-photon process. The shape function
and interacting with a strong squeezed field via four-photon process. The shape function 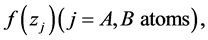 which describe the atomic motion for these atoms in the z-axis direction, and take the form [10] .
which describe the atomic motion for these atoms in the z-axis direction, and take the form [10] .
 (1)
(1)
where p₁ and p₂ are the atomic motion parameters, well, if we put p₁ = 1 and p2 = 0, then the shape function takes the form
 (2)
(2)
which means, there is no atomic motion inside the cavity, but if p₁ = 0 and p₂ = 1, the shape function will be
 (3)
(3)
hence, the atomic motion exists inside the cavity. The interaction Hamiltonian of moving two atoms interacting with a strong squeezed field via four-photon process with a closed system (In other words, there’s not any external fields or external effects can act on the system) in the rotating wave approximation RWA can be written as [9] (set ℏ = 1)
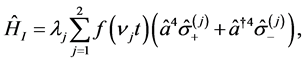 (4)
(4)
where 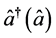 is the creation (annihilation) Boson’s operator,
is the creation (annihilation) Boson’s operator,  are the Pauli spin operators for
are the Pauli spin operators for 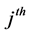 atom,
atom,  is the atom-field coupling constant of the
is the atom-field coupling constant of the 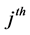 atom. We suppose that A, B and F denote the first atom, second atom and radiation field, respectively. We assume that the two atoms are initially in Bell state and the field in squeezed coherent state as follows
atom. We suppose that A, B and F denote the first atom, second atom and radiation field, respectively. We assume that the two atoms are initially in Bell state and the field in squeezed coherent state as follows
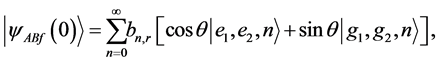 (5)
(5)
where
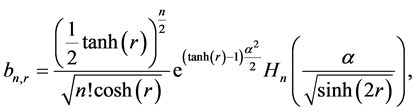
where r is the squeeze parameter. Using the above initial conditions, the wave function of the whole system  can be easily evaluated as
can be easily evaluated as
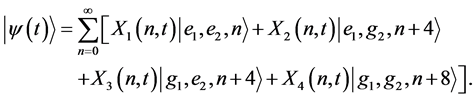 (6)
(6)
where
 (7)
(7)
 (8)
(8)
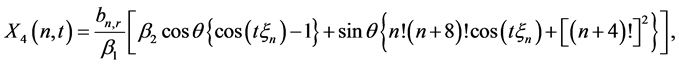 (9)
(9)
 (10)
(10)
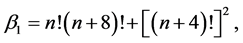 (11)
(11)
and
 (12)
(12)
Thus, one can obtain the atomic density matrix 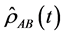 by tracing over the field, hence
by tracing over the field, hence
 (13)
(13)
where
 (14)
(14)
are an atomic occupation probabilities of levels  and
and  respectively, and
respectively, and

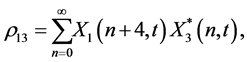
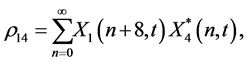
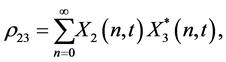

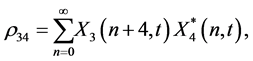
 (15)
(15)
In the following section, we use the relations obtained above to investigate the atoms-field entanglement through a statistical aspect, such as von Neumann entropy measurement for the system under consideration.
3. Von Neumann Entropy and Discussion
Due to the crucial role of entanglement in quantum information processes, the study of entanglement has attracted a lot of interest in recent years. Among the various studies on entanglement, the first question which may be asked is how to know that a quantum state is entangled. For a pure bipartite state, the Schmidt decomposition [11] can be used to judge whether the state is entangled and the degree of entanglement can be quantified by partial von Neumann entropy. We use the von Neumann entropy to measure the entanglement between two two-level atom and nonlinear optical field. The expression of the von Neumann entropy takes the form [12] [13]
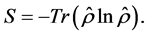
This is zero for all pure states, i.e., for states that satisfy the condition 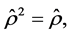 where
where 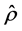 is the density operator describing a given quantum state. For this reason, this entropy cannot distinguish between various pure states, and it is rather a measure of the purity of quantum states. For the system under consideration, i.e.
is the density operator describing a given quantum state. For this reason, this entropy cannot distinguish between various pure states, and it is rather a measure of the purity of quantum states. For the system under consideration, i.e. 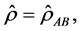 and the von Neumann entropy can be written as
and the von Neumann entropy can be written as
 (17)
(17)
where  are the eigenvalues of
are the eigenvalues of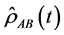 . The results of moving and non-moving two two-level identical atoms interacting with a strong squeezed field i.e. α = 5, via a four-photon process are introduced in Figure 1 and Figure 2 with different values of squeeze parameter r and two initial atomic states setting θ = 0, π/4 for excited and entangled atoms (Bell state), respectively.
. The results of moving and non-moving two two-level identical atoms interacting with a strong squeezed field i.e. α = 5, via a four-photon process are introduced in Figure 1 and Figure 2 with different values of squeeze parameter r and two initial atomic states setting θ = 0, π/4 for excited and entangled atoms (Bell state), respectively.
Since the excited identical atoms interacting with a squeezed field in the absence of atomic center-of-mass motion i.e.  Figure 1(b), Figure 1(c) show that the interaction takes irregular and unperiodic behavior with the time evolution λt, which called “a chaotic behavior”. This chaotic behavior appearance also if we put the squeeze parameter r = 0 and get a coherent field interacting with excited atoms as a special case in Figure 1(a).
Figure 1(b), Figure 1(c) show that the interaction takes irregular and unperiodic behavior with the time evolution λt, which called “a chaotic behavior”. This chaotic behavior appearance also if we put the squeeze parameter r = 0 and get a coherent field interacting with excited atoms as a special case in Figure 1(a).
However, if the atoms initially prepared in Bell state by setting 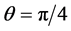 and interacting with a quantized fieldwe get also chaotic behavior in the presence or absence of squeezing in Figures 1(d)-1(f). Moreover, the interaction starting from zero and takes the maximum values of von Neumann entropy
and interacting with a quantized fieldwe get also chaotic behavior in the presence or absence of squeezing in Figures 1(d)-1(f). Moreover, the interaction starting from zero and takes the maximum values of von Neumann entropy  approximately 0.9 in Figure 1(a) and 0.7 in Figure 1(b), Figure 1(c), while the interaction starting from 0.5 in Figures 1(d)-1(f), the
approximately 0.9 in Figure 1(a) and 0.7 in Figure 1(b), Figure 1(c), while the interaction starting from 0.5 in Figures 1(d)-1(f), the

Figure 1. The von Neumann entropy 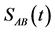 for the atoms-field entanglement and α = 5, since the atoms initially prepared in excited state θ = 0 with different values of squeezing parameter r where: Figure 1(a) r = 0, Figure 1(b) r = 1 and Figure 1(c) r = 2. Figures 1(d)-1(f) the same as Figures 1(a)-1(c) but the atoms in Bell state i.e. θ = π/4. The atomic motion parameters p₁ = 1 and p₂ = 0, i.e.
for the atoms-field entanglement and α = 5, since the atoms initially prepared in excited state θ = 0 with different values of squeezing parameter r where: Figure 1(a) r = 0, Figure 1(b) r = 1 and Figure 1(c) r = 2. Figures 1(d)-1(f) the same as Figures 1(a)-1(c) but the atoms in Bell state i.e. θ = π/4. The atomic motion parameters p₁ = 1 and p₂ = 0, i.e. 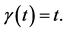

Figure 2. The von Neumann entropy 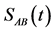 for the atoms-field entanglement and α = 5, since the atoms initially prepared in excited state θ = 0 with different values of squeezing parameter r where: Figure 1(a) r = 0, Figure 1(b) r = 1 and Figure 1(c) r = 2. Figures 1(d)-1(f) the same as Figures 1(a)-1(c) but the atoms in Bell state, i.e. θ = π/4. The atomic motion parameters p₁ = 1 and p₂ = 0 i.e.
for the atoms-field entanglement and α = 5, since the atoms initially prepared in excited state θ = 0 with different values of squeezing parameter r where: Figure 1(a) r = 0, Figure 1(b) r = 1 and Figure 1(c) r = 2. Figures 1(d)-1(f) the same as Figures 1(a)-1(c) but the atoms in Bell state, i.e. θ = π/4. The atomic motion parameters p₁ = 1 and p₂ = 0 i.e. 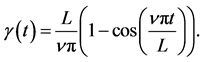
maximum values for von Neumann entropy equal one, i.e. , which the atomic initial state setting is very important to quantify the maximum degree of entanglement between atoms and field, so, the initial preparations for atoms in the Bell state is much better than the excited state for strongest entanglement through four-photon process, and the oscillation amplitudes can be weakened by more squeezing to coherent field and this is the useful thing about the squeeze parameter effects.
, which the atomic initial state setting is very important to quantify the maximum degree of entanglement between atoms and field, so, the initial preparations for atoms in the Bell state is much better than the excited state for strongest entanglement through four-photon process, and the oscillation amplitudes can be weakened by more squeezing to coherent field and this is the useful thing about the squeeze parameter effects.
By considering the atomic center-of-mass motion in Figure 2, i.e. 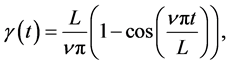 the results are reported us through von Neumann entropy measurement that the atoms-field entanglement takes a chaotic behavior, appearance for every periodic interval
the results are reported us through von Neumann entropy measurement that the atoms-field entanglement takes a chaotic behavior, appearance for every periodic interval  since the atoms in excited state as in Figures 2(a)-2(c), or in Bell state as in Figures 2(d)-2(f), with different values of squeeze parameter r. Also, we get a separable state, i.e.
since the atoms in excited state as in Figures 2(a)-2(c), or in Bell state as in Figures 2(d)-2(f), with different values of squeeze parameter r. Also, we get a separable state, i.e. 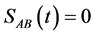 for every periodic interval
for every periodic interval 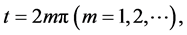 and entanglement sudden death (ESD) and birth (ESB) phenomenon appearance for periodic interval
and entanglement sudden death (ESD) and birth (ESB) phenomenon appearance for periodic interval  where
where  all that happened in Figures 2(a)-2(c) since the excited atoms interacting with a coherent field i.e. r = 0 shown in Figure 2(a), or interacting with a squeezed field in Figure 2(b), Figure 2(c), but since the atoms initially prepared in Bell state, the separable state, ESD and ESB are not existing in Figures 2(d)-2(f). Moreover, the interaction in Figures 2(a)-2(c) starting from zero and take the maximum values of
all that happened in Figures 2(a)-2(c) since the excited atoms interacting with a coherent field i.e. r = 0 shown in Figure 2(a), or interacting with a squeezed field in Figure 2(b), Figure 2(c), but since the atoms initially prepared in Bell state, the separable state, ESD and ESB are not existing in Figures 2(d)-2(f). Moreover, the interaction in Figures 2(a)-2(c) starting from zero and take the maximum values of  in Figure 2(a) approximately 0.9 and 0.7 in Figure 2(b), Figure 2(c), but in Figures 2(d)-2(f) the interaction starting from 0.5 in Figure 2(d) and from 0.7 in Figure 2(e), Figure 2(f), also, the maximum values of von Neumann
in Figure 2(a) approximately 0.9 and 0.7 in Figure 2(b), Figure 2(c), but in Figures 2(d)-2(f) the interaction starting from 0.5 in Figure 2(d) and from 0.7 in Figure 2(e), Figure 2(f), also, the maximum values of von Neumann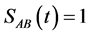 . On the other hand, the oscillations which appearance in von Neumann entropy in Figures 2(a)-2(c) can be weakened by more squeezing in coherent field, so, in Figure 2(b) the oscillation amplitude occur until 0.2 and 0.7, and by more squeezing in squeezed field, the oscillations getting weakened and occur in 0.5 and 0.7 in Figure 2(c), but in Figure 2(e), Figure 2(f) the oscillations occur in 0.7 and 1 for entangled atoms. It is clear that the sudden vanishing of entanglement at
. On the other hand, the oscillations which appearance in von Neumann entropy in Figures 2(a)-2(c) can be weakened by more squeezing in coherent field, so, in Figure 2(b) the oscillation amplitude occur until 0.2 and 0.7, and by more squeezing in squeezed field, the oscillations getting weakened and occur in 0.5 and 0.7 in Figure 2(c), but in Figure 2(e), Figure 2(f) the oscillations occur in 0.7 and 1 for entangled atoms. It is clear that the sudden vanishing of entanglement at 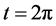 is due to its flow from one subspace to other ones. This phenomenon of the flow between various spaces were discussed in [34] in the absence of dissipation.
is due to its flow from one subspace to other ones. This phenomenon of the flow between various spaces were discussed in [34] in the absence of dissipation.
4. Conclusion
In summary, we have investigated the moving and non-moving two two-level identical atoms interacting with a squeezed coherent field via four-photon process in a closed system. The von Neumann entropy is used as a measure of the two atoms-field entanglement. The results show that some new important and interesting features of entanglement such as entanglement sudden birth and sudden death which can be obtained when the moving two atoms are initially in the excited state. Also, the entropy has a chaotic behavior in the presence or absence squeezing and atomic motion parameters. On the other hand, the initial state setting for the atomic position θ and squeeze parameter r playing an important role to get a high amount of entanglement since the atoms initially in Bell’s state. Our recommendation as an important future investigation will be the study of two atoms interacting with a squeezed field in the presence of the decoherence and the dipole-dipole interaction effects.
References
- Chao, W. and Mao-Fa, F. (2010) The Entanglement of Two Moving Atoms Interacting with a Single-Mode Field via a Three-Photon Process. Chinese Physics B, 19, Article ID: 020309. http://dx.doi.org/10.1088/1674-1056/19/2/020309
- Bashkirov, E.K., Sochkova, E.Y. and Litvinova, D.V. (2011) The Influence of Dipole-Dipole Interaction on the Sudden Death of Entanglement of Two Atoms with Degenerate Two-Photon Transitions. Pacific Science Review, 13, 255-259.
- Abdel-Khalek, S. and Obada, A.-S.F. (2009) The Atomic Wehrl Entropy of a V-Type Three-Level Atom Interacting with Two-Mode Squeezed Vacuum State. Journal of Russian Laser Research, 30, 146-156. http://dx.doi.org/10.1007/s10946-009-9066-1
- Abdel-Khalek, S., Abdel-Hameed, H.F. and Abdel-Aty, M. (2011) Atomic Wehrl Entropy of a Single Qubit System. International Journal of Quantum Information, 9, 967-979. http://dx.doi.org/10.1142/S0219749911007538
- Obada, A.-S.F. and Abdel-Khalek, S. (2004) New Features of the Atomic Wehrl Entropy and Its Density in Multiquanta Two-Level System. Journal of Physics A: Mathematical and General, 37, 6573. http://dx.doi.org/10.1088/0305-4470/37/25/010
- López, C.E., Romero, G., Lastra, F., Solano, E. and Retamal, J.C. (2008) Sudden Birth versus Sudden Death of Entanglement in Multipartite Systems. Physical Review Letters, 101, Article ID: 080503. http://dx.doi.org/10.1103/PhysRevLett.101.080503
- Gerry, C. and Knight, P. (2005) Introductory Quantum Optics. University Press, Cambridge.
- Ye, Y.-H., Li, Z.-J. and Zeng, G.-J. (2008) A Measure of Non-Classicality of Even and Odd Coherent States. Chinese Physics Letters, 25, 1175. http://dx.doi.org/10.1088/0256-307X/25/4/004
- Wu, C. and F, M.-F. (2010) The Entanglement of Two Moving Atoms Interacting with a Single-Mode Field via a Three-Photon Process. Chinese Physics B, 19, Article ID: 020309. http://dx.doi.org/10.1088/1674-1056/19/2/020309
- Abdel-Khalek, S. (2008) The Effect of Atomic Motion and Two-Quanta JCM on the Information Entropy. Physica A, 387, 779-786. http://dx.doi.org/10.1016/j.physa.2007.09.034
- Bennett, C.H., Berstein, H.J., Popescu, S. and Schumacher, B. (1996) Concentrating Partial Entanglement by Local Operation. Physical Review A, 53, 2046-2052. http://dx.doi.org/10.1103/PhysRevA.53.2046
- von Neumann, J. (1955) Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton.
- Phoenix, S.J.D. and Knight, P.L. (1988) Fluctuations and Entropy in Models of Quantum Optical Resonance. Annals of Physics (New York), 186 381-407. http://dx.doi.org/10.1016/0003-4916(88)90006-1
- Braunstein, L. and Caves, C.M. (1988) Information Theoretic Bell Inequalities. Physical Review Letters, 61, 662-665. http://dx.doi.org/10.1103/PhysRevLett.61.662
- Benenti, G., Casati, G. and Strini, G. (2007) Principles of Quantum Computation and Information, Volume. II: Basic Tools and Special Topics. World Scientific, Singapore City.
- Nielsen, M.A. and Chuang, I.L. (2010) Quantum Computation and Quantum Information. 10th Anniversary Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511976667
- Ekert, A. (1991) Quantum Cryptography Based on Bell’s Theorem. Physical Review Letters, 68, 661-663. http://dx.doi.org/10.1103/PhysRevLett.67.661
- Cirac, J.I. and Gisin, N. (1997) Coherent Eavesdropping Strategies for the Four State Quantum Cryptography Protocol. Physics Letters A, 229, 1-7. http://dx.doi.org/10.1016/S0375-9601(97)00176-X
- Fuchs, C.A., Gisin, N., Griffiths, R.B., Niu, C.-S. and Peres, A. (1997) Optimal Eavesdropping in Quantum Cryptography. I. Information Bound and Optimal Strategy. Physical Review A, 56, 1163-1172. http://dx.doi.org/10.1103/PhysRevA.56.1163
- Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A. and Wootters, W.K. (1993) Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Physical Review Letters, 70, 1895-1899. http://dx.doi.org/10.1103/PhysRevLett.70.1895
- Mozes, S., Oppenheim, J. and Reznik, B. (2005) Deterministic Dense Coding with Partial Entangled State. Physical Review A, 71, Article ID: 012311. http://dx.doi.org/10.1103/PhysRevA.71.012311
- Ye, L. and Guo, C.C. (2005) Scheme for Implementing Quantum Dense Coding in Cavity QED. Physical Review A, 71, 034304. http://dx.doi.org/10.1103/PhysRevA.71.034304
- Shannon, C.E. and Weaver, W. (1949) The Mathematical Theory of Cummunications. Urbana University Press, Chicago.
- Abdel-Khalek, S. (2007) Atomic Wehrl Entropy in a Two-Level Atom Interacting with a Cavity Field. Applied Mathematics & Information Sciences, 1, 53-64
- Abdel-Khalek, S., Barzanjeh, S., Eleuch, H. (2011) Entanglement Sudden Death and Sudden Birth in Semiconductor Microcavities. International Journal of Theoretical Physics, 50, 2939-2950. http://dx.doi.org/10.1007/s10773-011-0794-y
- Berrada, K., Chafik, A., Eleuch, H. and Hassouni, Y. (2010) Concurrence in the Framework of Coherent States. Quantum Information Processing, 9, 13-26. http://dx.doi.org/10.1007/s11128-009-0124-y
- Berrada, K., Mohammadzade, A., Abdel-Khalek, S., Eleuch, H. and Salimi, S. (2012) Nonlocal Correlations for Manifold Quantum Systems: Entanglement of Two-Spin States. Physica E: Low-dimensional Systems and Nanostructures, 45, 21-27. http://dx.doi.org/10.1016/j.physe.2012.06.014
- Berrada, K., Eleuch, H. and Hassouni, Y. (2011) Asymtotic Dynamics of Quantum Discord in Open Quantum Systems. Journal of Physics B: Atomic, Molecular and Optical Physics, 44, Article ID: 145503. http://dx.doi.org/10.1088/0953-4075/44/14/145503
- Obada, A.S.F. and Abdel-Khalek, S. (2010) Entanglement Evaluation with Atomic Fisher information. Physica A: Statistical Mechanics and Its Applications, 389, 891-898. http://dx.doi.org/10.1016/j.physa.2009.09.015
- Obada, A.S.F., Abdel-Khalek, S. and Plastino, A. (2011) Information Quantifiers’ Description of Weak Field vs. Strong Field Dynamics for a Trapped Ion in a Laser Field. Physica A: Statistical Mechanics and Its Applications, 390, 525-533. http://dx.doi.org/10.1016/j.physa.2010.09.003
- Abdel-Khalek, S. (2013) Quantum Fisher information for Moving Three-Level Atom. Quantum Information Processing, 12, 3761-3769. http://dx.doi.org/10.1007/s11128-013-0622-9
- Obada, A.S.F., Abdel-Khalek, S., Berrada, K. and Shaheen, M.E. (2013) Investigations of Information Quantifiers for the Tavis-Cummings Model. Physica A: Statistical Mechanics and Its Applications, 392, 6624-6632. http://dx.doi.org/10.1016/j.physa.2013.07.051
- Obada, A.S.F., Abdel-Khalek, S. and Abo-Kahla, D.A.M. (2010) New Features of Entanglement and Other Applications of a Two-Qubit System. Optics Communications, 283, 4662-4670. http://dx.doi.org/10.1016/j.optcom.2010.06.074
- Kowalewska-Kudlaszyk, A., Leonski, W. and Jr, J.P. (2011) Photon-Number Entangled States Generated in Kerr Media with Optical Parametric Pumping. Physical Review A, 83, Article ID: 052326. http://dx.doi.org/10.1103/PhysRevA.83.052326
NOTES

*Corresponding author.

