Natural Science
Vol.6 No.1(2014), Article ID:42373,6 pages DOI:10.4236/ns.2014.61004
Designing mixed  structure specified controllers using Particle Swarm Optimization (PSO) algorithm
structure specified controllers using Particle Swarm Optimization (PSO) algorithm
1Electrical and Electronics Department, Engineering College, Thi-Qar, Iraq; a.n.younis@live.com
2Iraq University College, Basra, Iraq
Copyright © 2014 Ayman N. Salman Younis et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Ayman N. Salman Younis et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 15 June 2013; revised 15 July 2013; accepted 25 July 2013
ABSTRACT
This paper proposes an efficient method for designing accurate structure-specified mixed  optimal controllers for systems with uncertainties and disturbance using particle swarm (PSO) algorithm. It is designed to find a suitable controller that minimizes the performance index of error signal subject to an unequal constraint on the norm of the closed-loop system. Although the mixed
optimal controllers for systems with uncertainties and disturbance using particle swarm (PSO) algorithm. It is designed to find a suitable controller that minimizes the performance index of error signal subject to an unequal constraint on the norm of the closed-loop system. Although the mixed  for the output feedback approach control is considered as a robust and optimal control technique, the design process normally comes up with a complex and non-convex optimization problem, which is difficult to solve by the conventional optimization methods. The PSO can efficiently solve design problems of multi-input-multi-output (MIMO) optimal control systems, which is very suitable for practical engineering designs. It is used to search for parameters of a structure-specified controller, which satisfies mixed
for the output feedback approach control is considered as a robust and optimal control technique, the design process normally comes up with a complex and non-convex optimization problem, which is difficult to solve by the conventional optimization methods. The PSO can efficiently solve design problems of multi-input-multi-output (MIMO) optimal control systems, which is very suitable for practical engineering designs. It is used to search for parameters of a structure-specified controller, which satisfies mixed 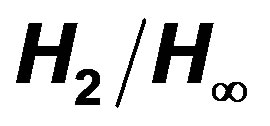 performance index. The simulation and experimental results show high feasibility, robustness and practical value compared with the conventional proportional-integral-derivative (PID) and proportional-Integral (PI) controller, and the proposed algorithm is also more efficient compared with the genetic algorithm (GA).
performance index. The simulation and experimental results show high feasibility, robustness and practical value compared with the conventional proportional-integral-derivative (PID) and proportional-Integral (PI) controller, and the proposed algorithm is also more efficient compared with the genetic algorithm (GA).
KEYWORDS
Mixed 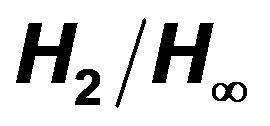 Optimal Control; Particle Swarm Optimization Algorithm; Structure-Specified Controller
Optimal Control; Particle Swarm Optimization Algorithm; Structure-Specified Controller
1. INTRODUCTION
Recently, mixed 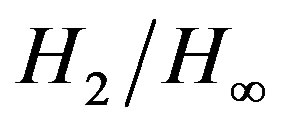 optimal control problems have received a great deal of attention from the viewpoint of theoretical design because it is an advanced technique for designing robust and optimal controllers for systems associated with sources of uncertainties. It was firstly proposed by Bernstein [1], and has been further developed by many researchers [2,3]. Although GA is a useful tool for solving optimization problems and has been applied successfully in many control systems, it still has limitations due to its stochastic searching characteristic and complex computation that make it slow convergence to global optimum. PSO is a powerful method for solving complex and ill-defined optimization problems because of its oriented searching and simple computation search [4]. Many researchers have become increasingly interested in the use of PSO as a means to design various classes of control systems. Kao [5] used PSO to design a self-tuning PID controller for a slidercrank mechanism. Chang [6] used PSO to design a PID controller for chaotic synchronization. In this paper, we propose a method to design the structure-specified mixed
optimal control problems have received a great deal of attention from the viewpoint of theoretical design because it is an advanced technique for designing robust and optimal controllers for systems associated with sources of uncertainties. It was firstly proposed by Bernstein [1], and has been further developed by many researchers [2,3]. Although GA is a useful tool for solving optimization problems and has been applied successfully in many control systems, it still has limitations due to its stochastic searching characteristic and complex computation that make it slow convergence to global optimum. PSO is a powerful method for solving complex and ill-defined optimization problems because of its oriented searching and simple computation search [4]. Many researchers have become increasingly interested in the use of PSO as a means to design various classes of control systems. Kao [5] used PSO to design a self-tuning PID controller for a slidercrank mechanism. Chang [6] used PSO to design a PID controller for chaotic synchronization. In this paper, we propose a method to design the structure-specified mixed  controllers by using PSO algorithm. The aims of this design are to obtain both robust stability and good performance, for instances, small tracking error, less control energy, etc. In the method, model uncertainty of the system is represented by multiplicative uncertainty, and the system is assumed to be affected by external unit step disturbances and then the structure-specified controller is defined. Finally, PSO is used to search for parameters of an admissible structure-specified controller that minimizes the integral of squared error (H2 norm) subjected to robust stability constraints (H∞ norm) against model uncertainty and external disturbances. The paper is organized as follows. Section 2, 3 and 4 explain a systematic procedure of the proposed controllers design algorithm. Simulation and results are presented in Section 5. Finally, Section 6 concludes the paper.
controllers by using PSO algorithm. The aims of this design are to obtain both robust stability and good performance, for instances, small tracking error, less control energy, etc. In the method, model uncertainty of the system is represented by multiplicative uncertainty, and the system is assumed to be affected by external unit step disturbances and then the structure-specified controller is defined. Finally, PSO is used to search for parameters of an admissible structure-specified controller that minimizes the integral of squared error (H2 norm) subjected to robust stability constraints (H∞ norm) against model uncertainty and external disturbances. The paper is organized as follows. Section 2, 3 and 4 explain a systematic procedure of the proposed controllers design algorithm. Simulation and results are presented in Section 5. Finally, Section 6 concludes the paper.
2. STRUCTURE-SPECIFIED MIXED 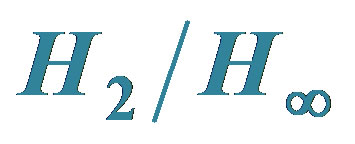 CONTROL
CONTROL
Consider a system with 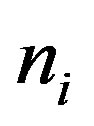 inputs and
inputs and 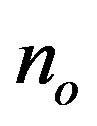 outputs controlled system as shown in Figure 1, where
outputs controlled system as shown in Figure 1, where 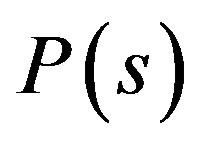 is nominal plant model,
is nominal plant model, 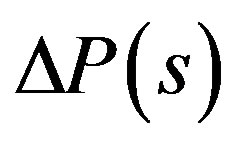 is plant perturbation,
is plant perturbation, 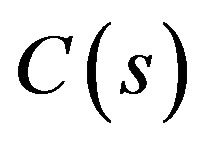 is controller,
is controller, 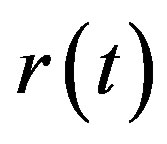 is reference input,
is reference input, 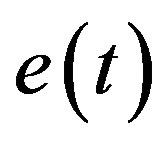 is trackingerror,
is trackingerror, 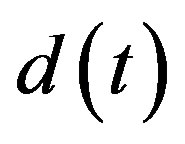 is external disturbance, and
is external disturbance, and 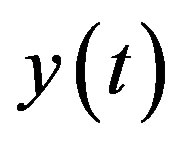 is output of the system [7]. The plant perturbation
is output of the system [7]. The plant perturbation  is assumed upper bounded by a known stable weighting function matrix
is assumed upper bounded by a known stable weighting function matrix 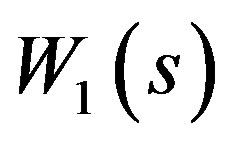
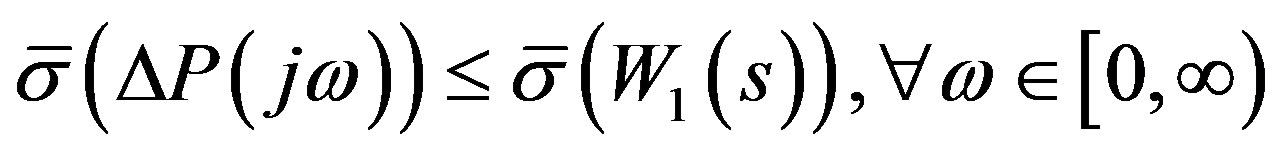 (1)
(1)
where 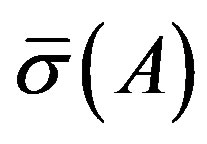 denotes the maximum singular value of a matrix
denotes the maximum singular value of a matrix .
.
It is proved that if a controller 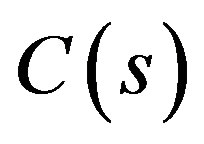 is designed so that:
is designed so that:
1) The nominal closed-loop system (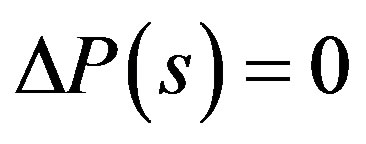 and
and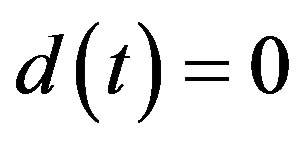 ) is asymptotically stable.
) is asymptotically stable.
2) The robust stability performance against plant perturbation satisfies the following inequality
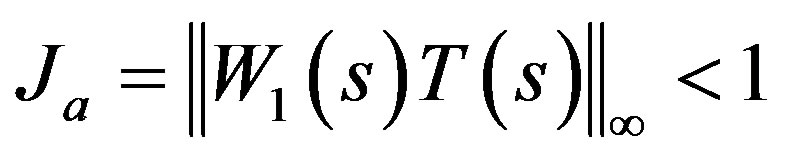 (2)
(2)
3) The disturbance attenuation performance satisfies the following inequality
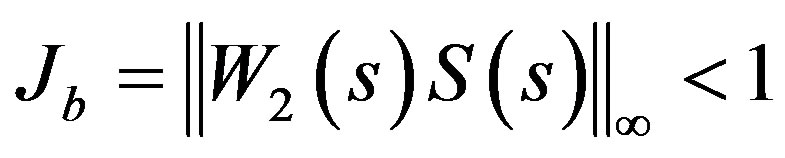 (3)
(3)
Then, the closed-loop system is also asymptotically stable with  and
and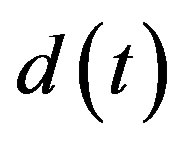 , where
, where 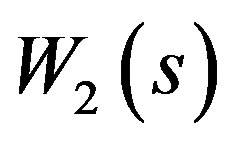 is a stable weighting function matrix specified by the designers.
is a stable weighting function matrix specified by the designers. 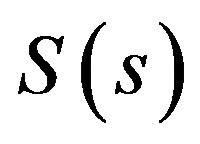 and
and  are the sensitivity functions, and the complementary sensitivity of the system, respectively [8]
are the sensitivity functions, and the complementary sensitivity of the system, respectively [8]
 (4)
(4)
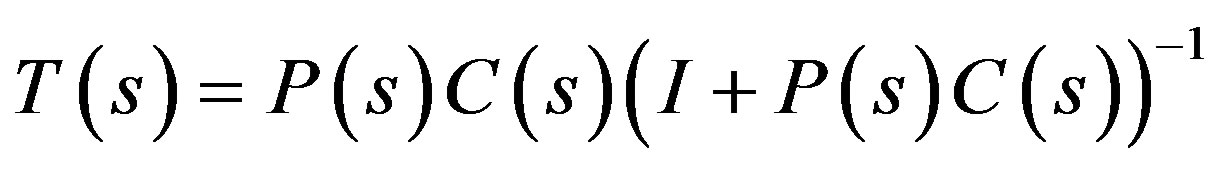 (5)
(5)
In many control systems, not only the robust stability against plant perturbation and external disturbancesbut also small tracking error is also important. The problem of minimizing the tracking error of a system can be defined as minimizing the cost function, called the integral of the squared error (ISE)
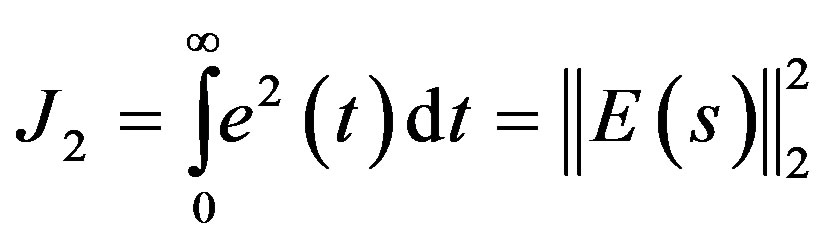 (6)
(6)
where 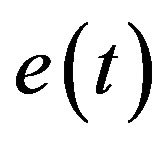 is the system error between input and output which can be obtain from inverse Laplace transformation of
is the system error between input and output which can be obtain from inverse Laplace transformation of  with
with  and
and 
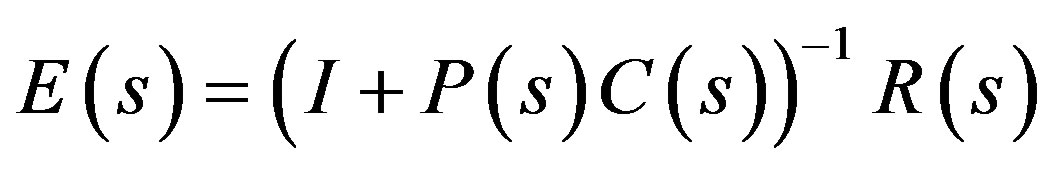 (7)
(7)
The handling of constraints in Equation (2), and Equation (3) is to recast the constraints as objectives tobeminimized and, consequently, a weighted sum approach is conveniently used with suitable weightings 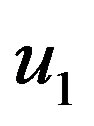 and
and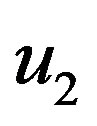 , which can be calculated by the designer. Therefore, the objective function of the investigated problem of designing mixed
, which can be calculated by the designer. Therefore, the objective function of the investigated problem of designing mixed 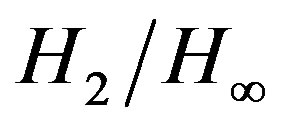 optimal controllers will be as follows
optimal controllers will be as follows
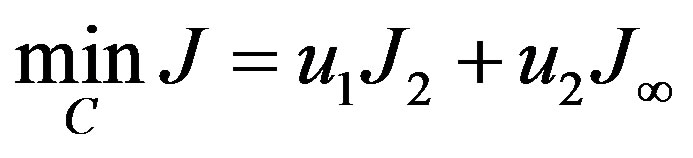 (8)
(8)
In this paper, the value of 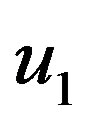 and
and 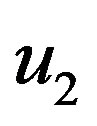 is chosen equal to 1, and a suitable structure specified PID controller will be chosen depending on the number of the inputs and the number of the outputs.
is chosen equal to 1, and a suitable structure specified PID controller will be chosen depending on the number of the inputs and the number of the outputs.
3. PSO ALGORITHM
Particle swarm optimization is a heuristic global optimization method and also an optimization algorithm, which is based on swarm intelligence. It comes from the research on the bird and fish flock movement behavior. In an initial moment, all the particles are positioned randomly in the searching space, in which the solution must be. The movement of each particle is the result of a vector sum of three distinct terms; the first contribution is related to the inertia of the particle (a particle’s personal component), the second is related to the best position occupied by the particle (a personal component-memory) and the third is relative to the best position found by the group (group contribution-cooperation). Let the search space be 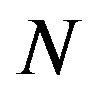 -dimensional, and the particle i is represented by an
-dimensional, and the particle i is represented by an 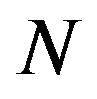 -dimensional position vector
-dimensional position vector
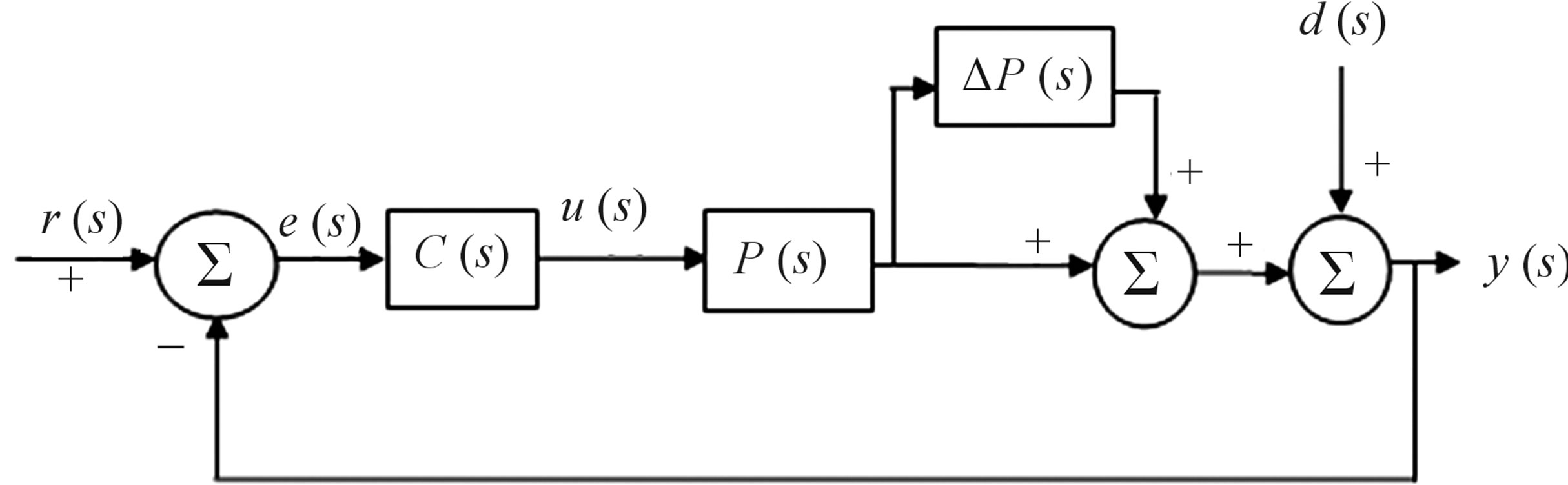
Figure 1. Control system with plant perturbation and external disturbance.
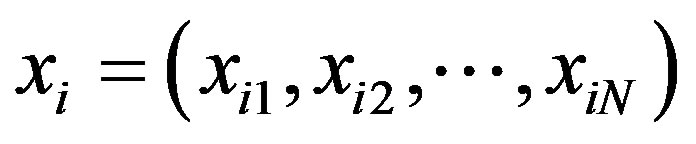 . The velocity is represented by an
. The velocity is represented by an 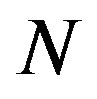 -dimensional velocity vector
-dimensional velocity vector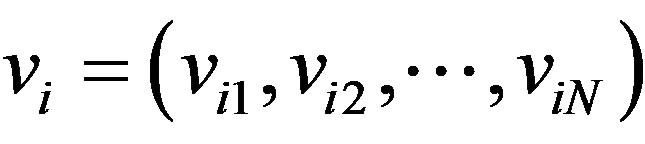 . The fitness of particles is evaluated by the objective function of the optimization problem. The best previously function of the optimization problem. The best previously visited position of particle
. The fitness of particles is evaluated by the objective function of the optimization problem. The best previously function of the optimization problem. The best previously visited position of particle 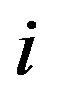 is noted as its individual best position,
is noted as its individual best position,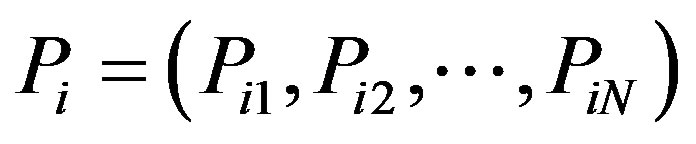 . The position of the best individual of the whole swarm is noted as the global best position,
. The position of the best individual of the whole swarm is noted as the global best position, . At each step of searching process, the velocity of particle and its new position are updated according to the following two equations [9]
. At each step of searching process, the velocity of particle and its new position are updated according to the following two equations [9]
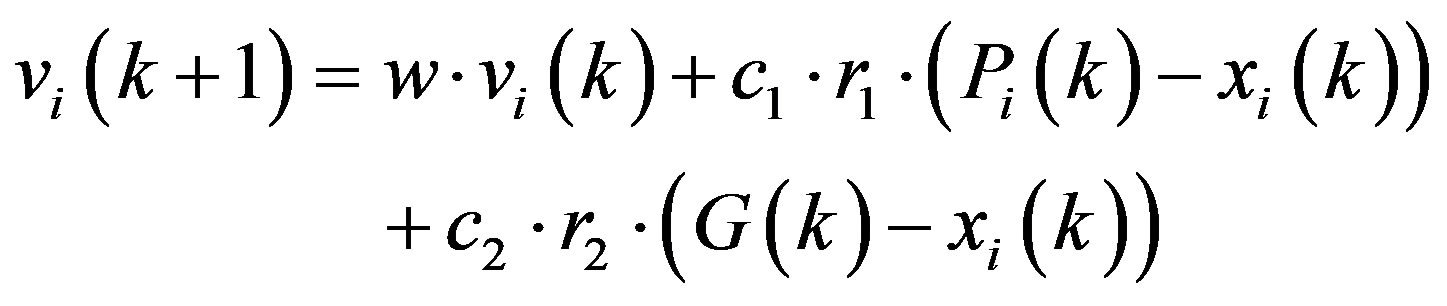 (9)
(9)
 (10)
(10)
where w, called inertia weight, controls the impact of previous velocity of the particle.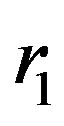 ,
, 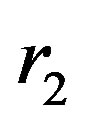 are random variables in the range of [0, 1].
are random variables in the range of [0, 1].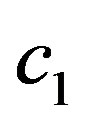 ,
, 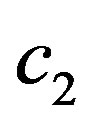 are positive constant parameters called acceleration coefficients. The value of each component in v is limited to the range
are positive constant parameters called acceleration coefficients. The value of each component in v is limited to the range 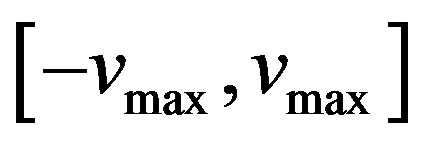 to control excessive roaming of particles outside the search space.
to control excessive roaming of particles outside the search space.
4. PSO-BASED STRUCTURE-SPECIFIED MIXED 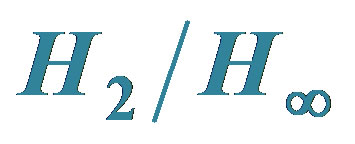 CONTROL
CONTROL
A procedure for designing PSO-based structure-specified mixed 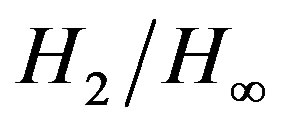 controllers for the problem defined in Section 3.1 is presented below.
controllers for the problem defined in Section 3.1 is presented below.
Step 1: Define a structure-specified controller of the form
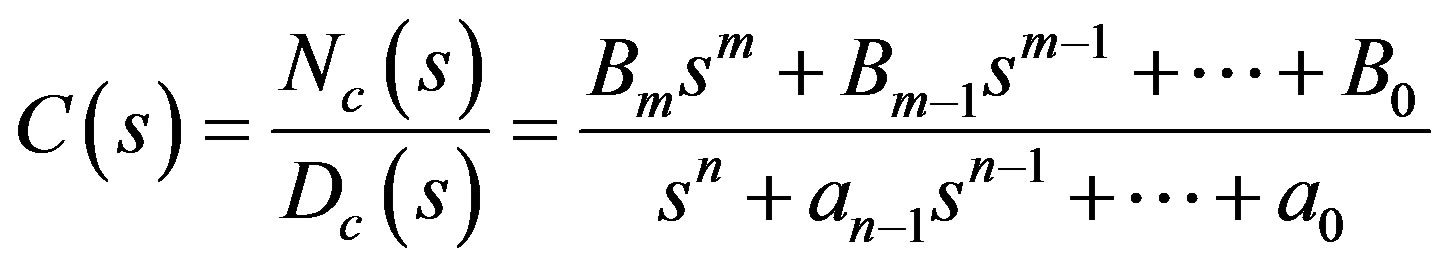 (11)
(11)
and specify the upper bound of plant uncertainty,  , weighting function for disturbance rejection,
, weighting function for disturbance rejection,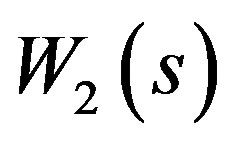 .
.
Step 2: Set particle  to
to
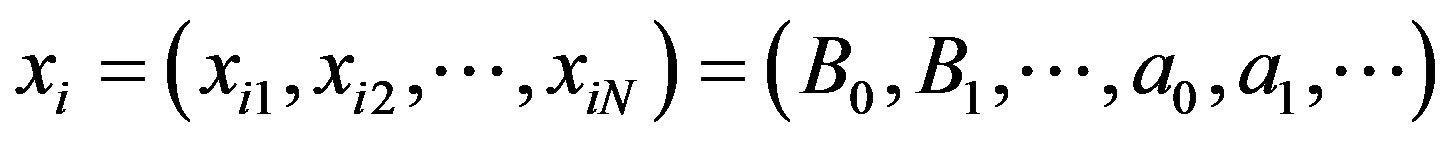 , the number of parameters of the controller in Equation (11) is the dimension of particle,
, the number of parameters of the controller in Equation (11) is the dimension of particle, .
.
Step 3: Initialize a random swarm of  particles as
particles as 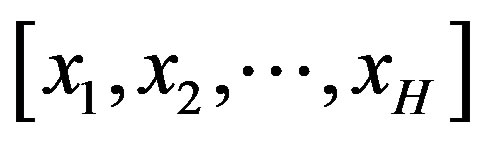 when the swarm size is set to
when the swarm size is set to .
.
Step 4: For each generation, evaluate objective function of each particle using the objective function expressed in (6), and also evaluate the constraints (2) and (3). The cost function can then be calculated as following:
• If 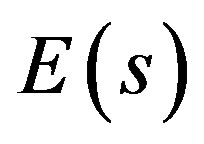 has right half-plane poles, then set
has right half-plane poles, then set 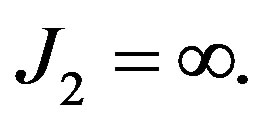
• If 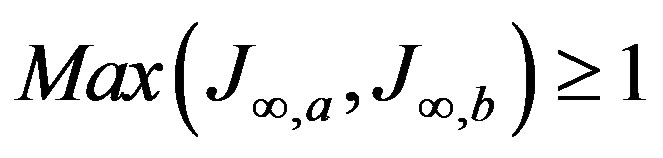 then set
then set 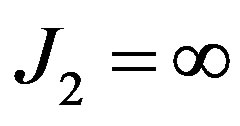 else
else 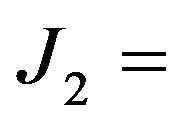
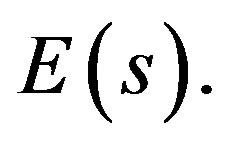 Determine the individual best, and the global best.
Determine the individual best, and the global best.
Step 5: Update the velocity of particle and its new position using (9) and (10).
Step 6: When the maximum number of iterations is arrived, stop the algorithm. Otherwise, go to Step 4.
5. SIMULATION RESULTS
In this section, an PID and PI examples are given to illustrate the proposed design procedures and a comparison study with GA algorithm is carried out to illustrate the effectiveness. Consider a highly coupled distillation column model [8]
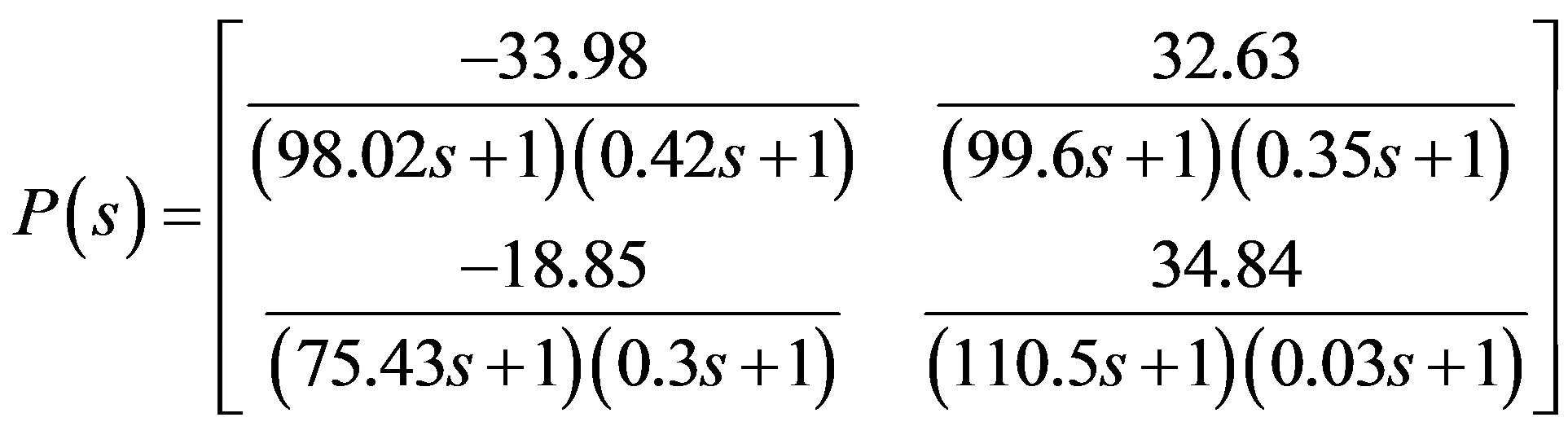 (12)
(12)
The bound 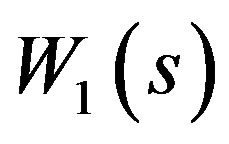 of the plant uncertainties
of the plant uncertainties 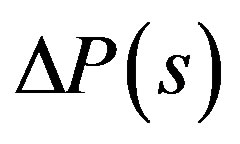 is
is
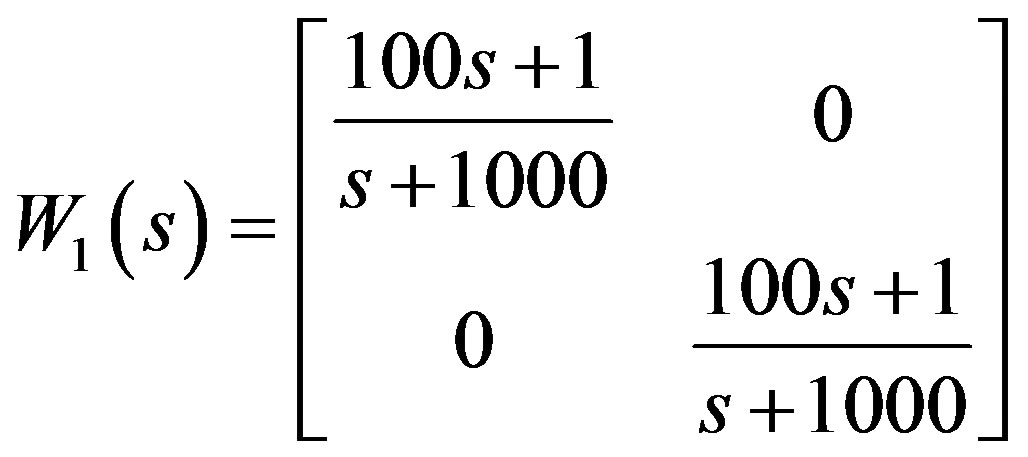 (13)
(13)
To attenuate disturbance, the stable weighting function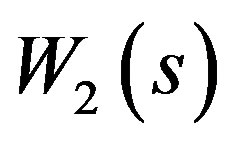 is chosen as
is chosen as
 (14)
(14)
5.1. PI Problem
Since there are 2-inputs and 2-outputs, the structuredspecified PI controller will be
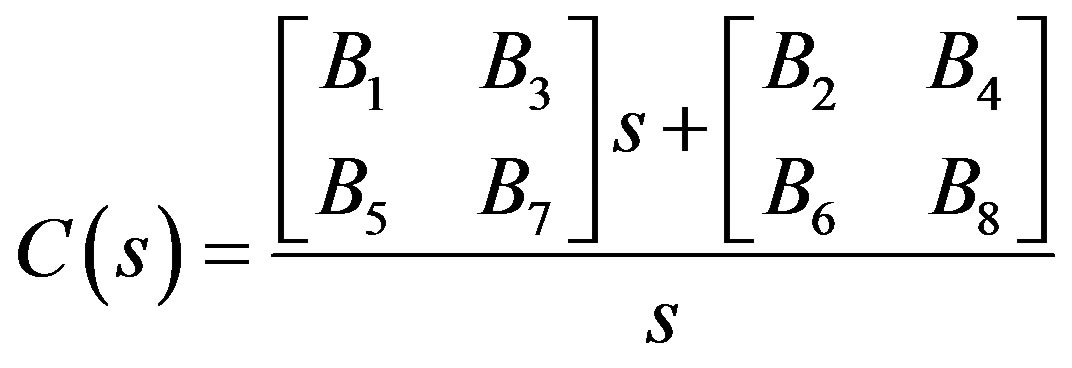
A typical controller 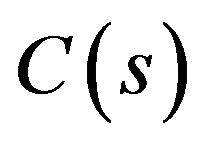 obtained from the POSbased method with 10 runs
obtained from the POSbased method with 10 runs

With the following value of performance indices 
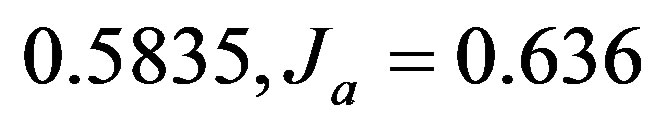 , and
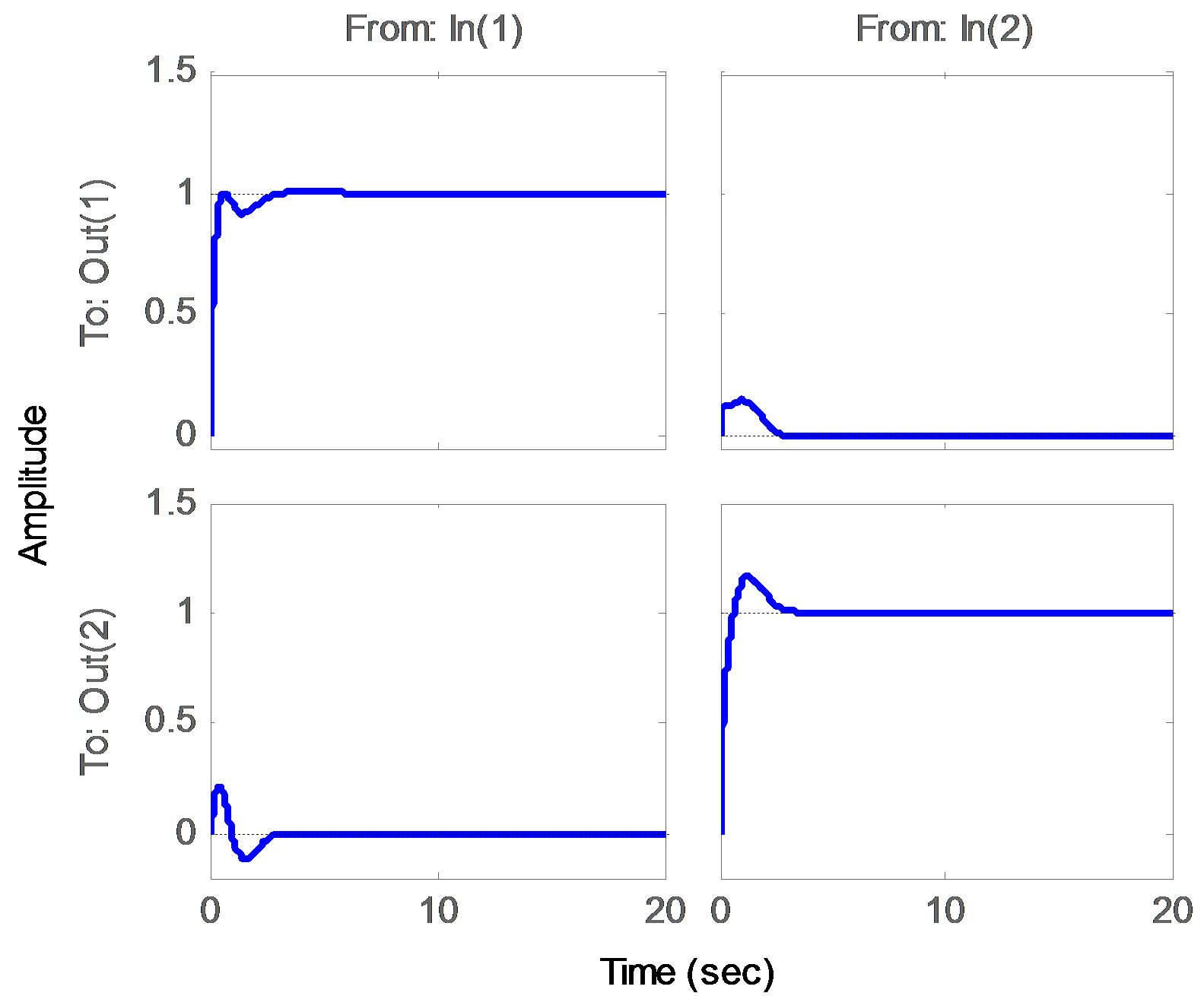
, and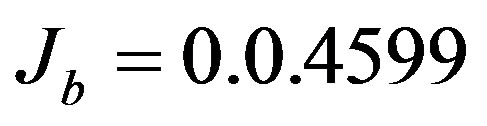 . The step response, the disturbance response, and Step response with the following value uncertainty for the resultant system using PSO is shown in Figures 2(a)-(d).
. The step response, the disturbance response, and Step response with the following value uncertainty for the resultant system using PSO is shown in Figures 2(a)-(d).
5.2. PID Problem
Since there are 2-inputs and 2-outputs the structuredspecified PI controller will be
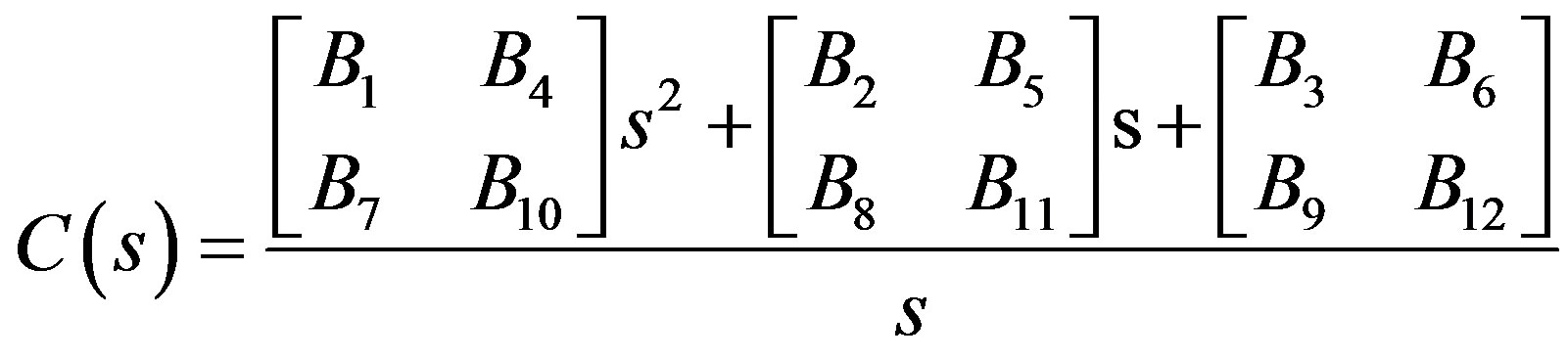
A typical controller 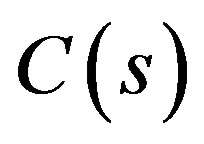 obtained from the PSObased method with 10 runs (equation at the end of the page).
obtained from the PSObased method with 10 runs (equation at the end of the page).
The step response, the disturbance response, and step response with the following value uncertainty of the resultant system using PSO is shown in Figures 3(a)-(d). Table 1 shows the statistical results from the 10 runs of problems 1 and 2. Figure 4 shows the convergence of the best trial from both PSO-based and GA-based algorithms. It can be seen that PSO-based algorithm is convergent at about 30 generations whereas GA-based algorithm takes about 45 generations.
6. CONCLUSION
This paper proposed a PSO-based algorithm for designing structure-specified mixed 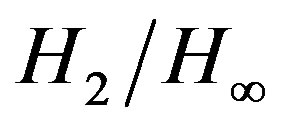 MIMO controllers with robust stability and disturbance attenuation. The high performance and validity of the proposed method are demonstrated by a MIMO system with PI and
MIMO controllers with robust stability and disturbance attenuation. The high performance and validity of the proposed method are demonstrated by a MIMO system with PI and
 (a)
(a)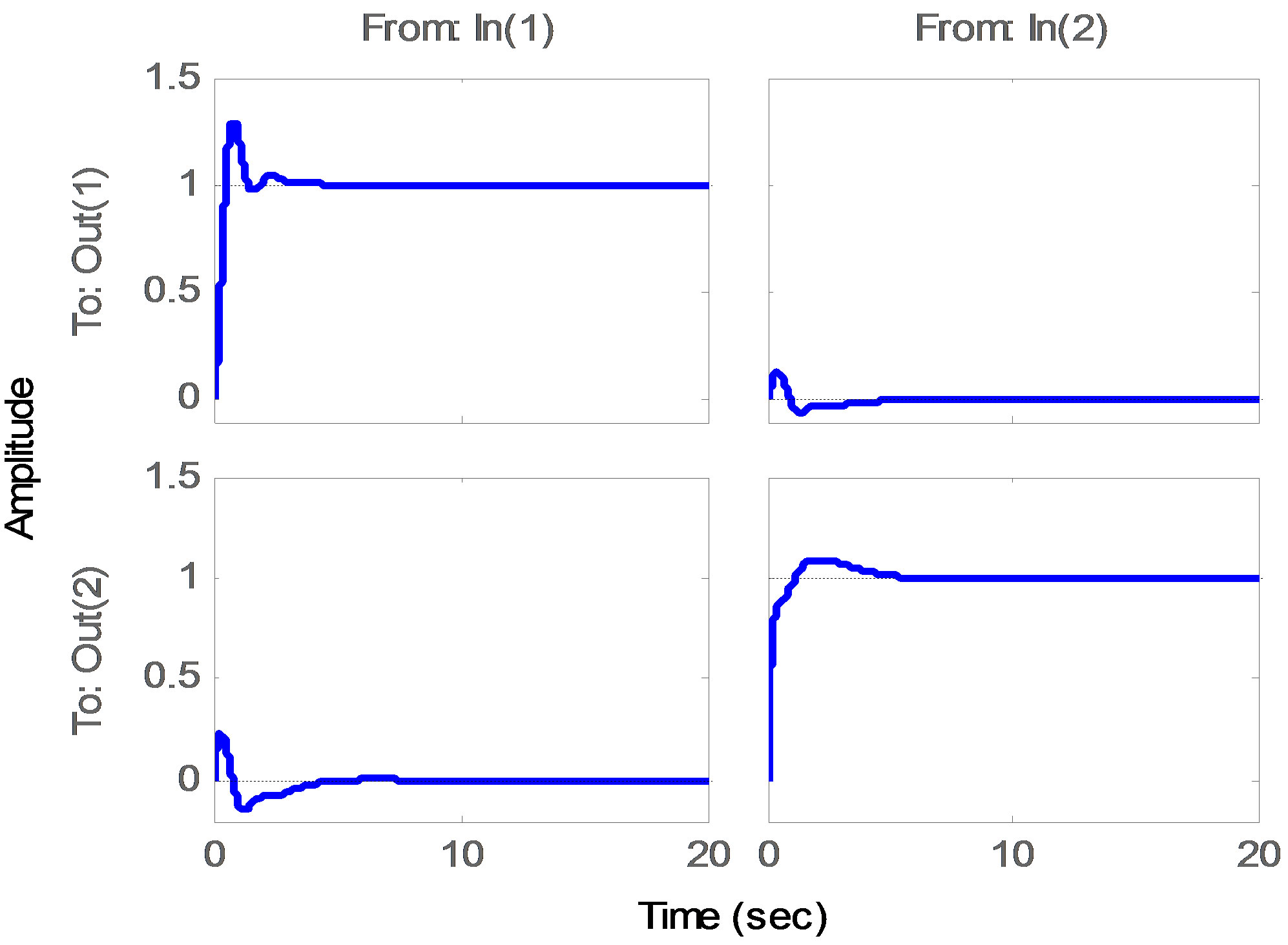 (b)
(b) (c)
(c)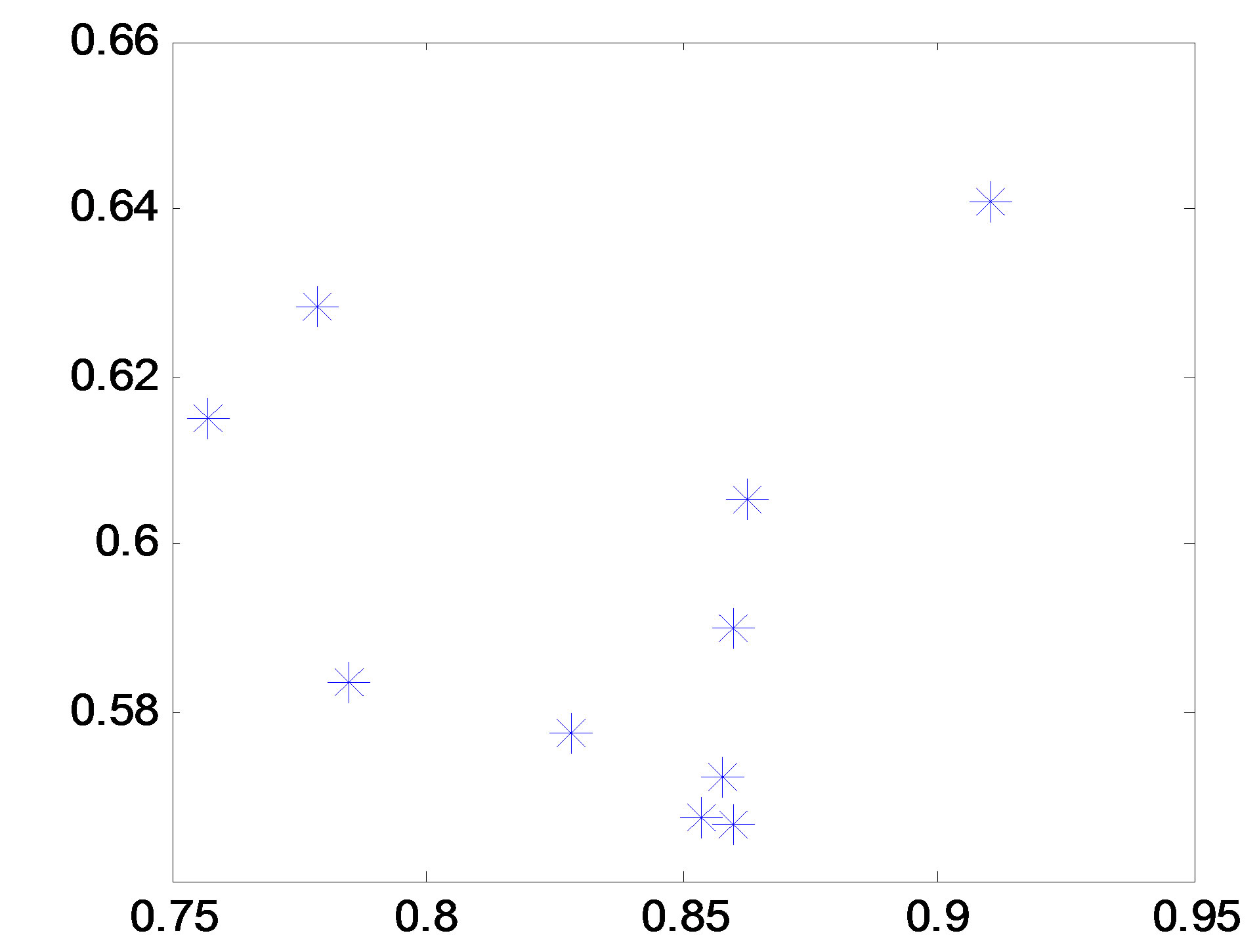 (d)
(d)
Figure 2. Output response for example 1. (a) PI step response; (b) PI disturbance response; (c) PI Step response with uncertainty; (d) Distribution of the ten PI controllers.
|
|
 (a)
(a)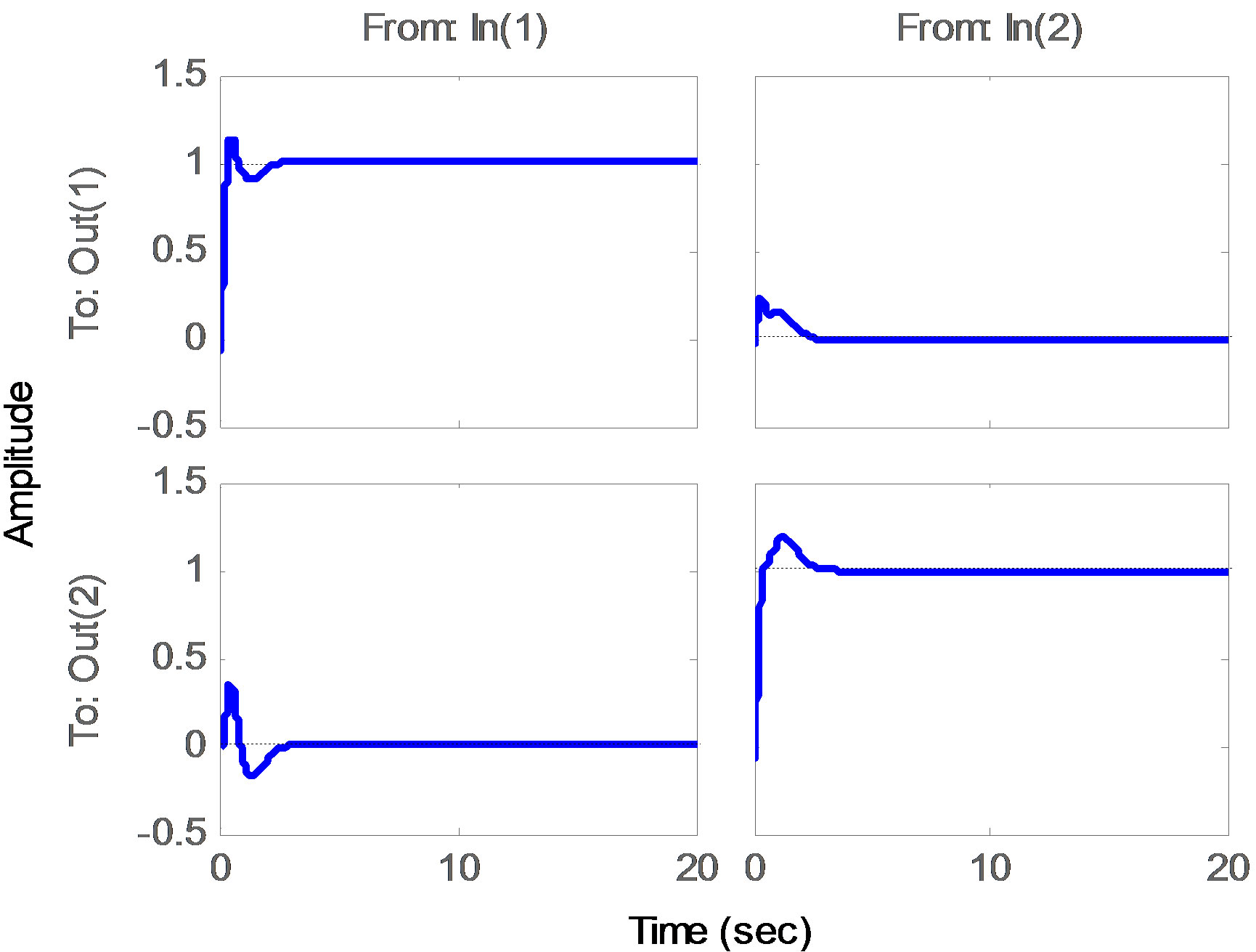 (b)
(b)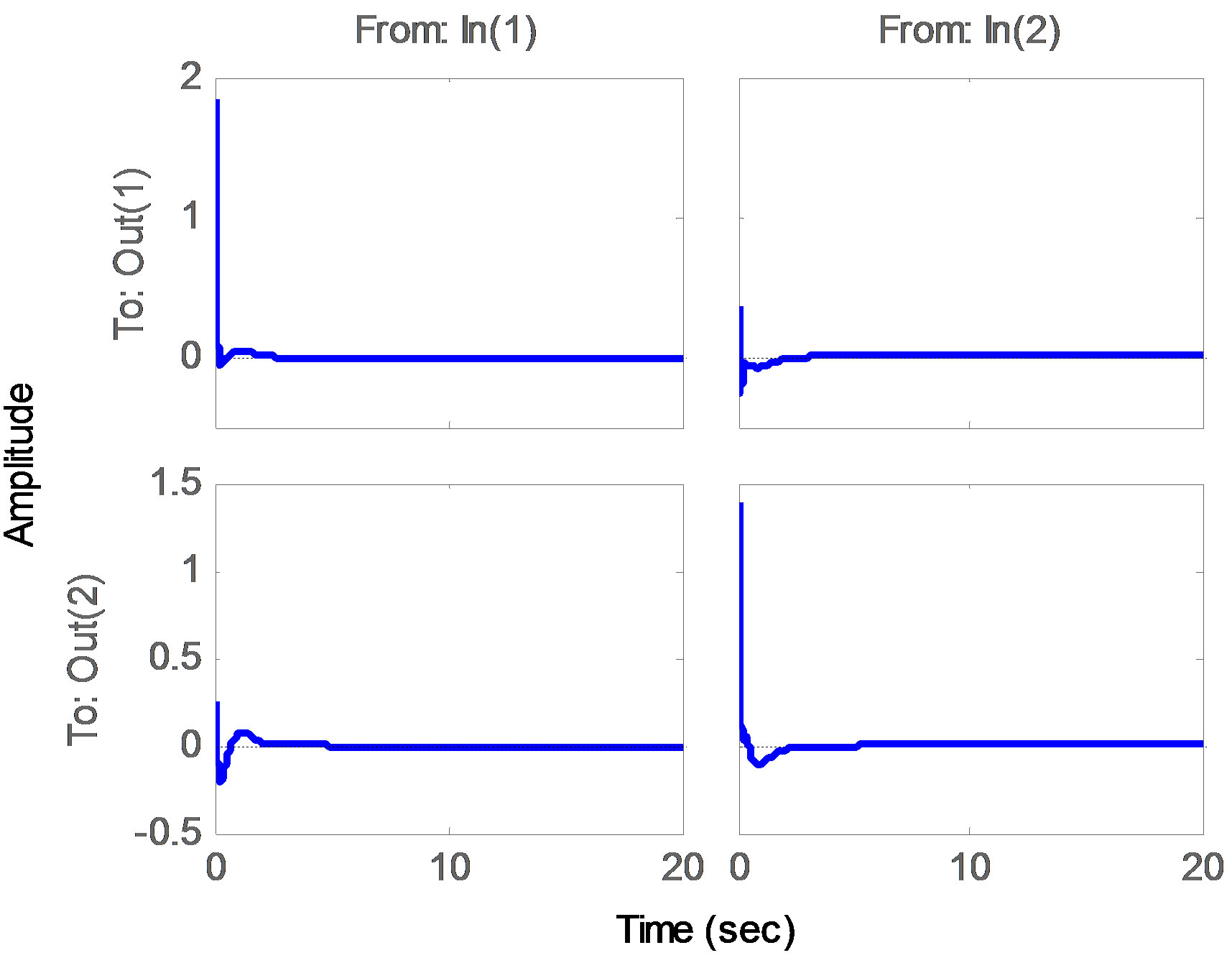 (c)
(c)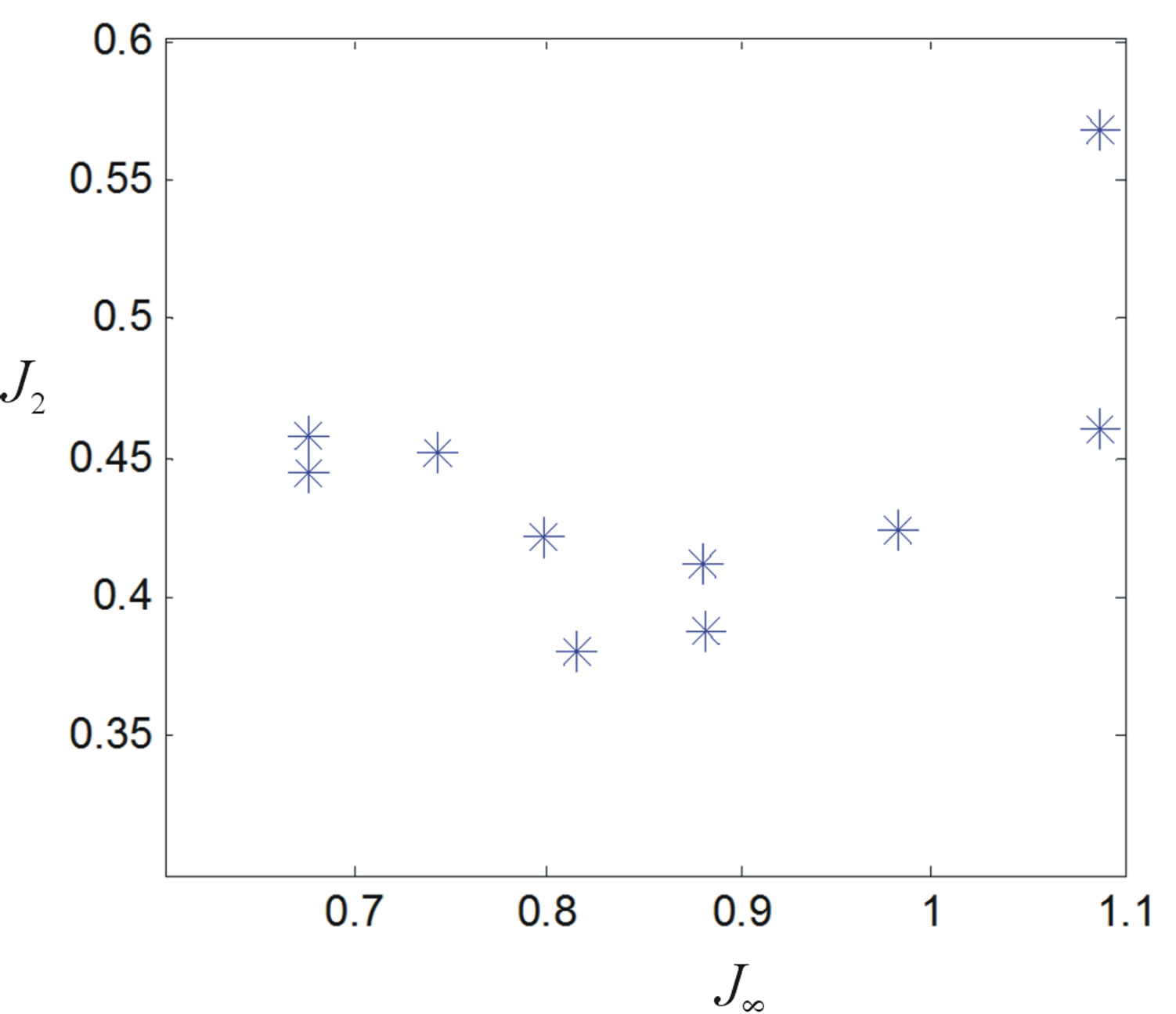 (d)
(d)
Figure 3. Output response for example 2. (a) PID step response; (b) PID disturbance response; (c) PID Step response with uncertainty; (d) Distribution of the ten PID controllers.

Table 1. Performance of the pso-based controller from 10 runs.
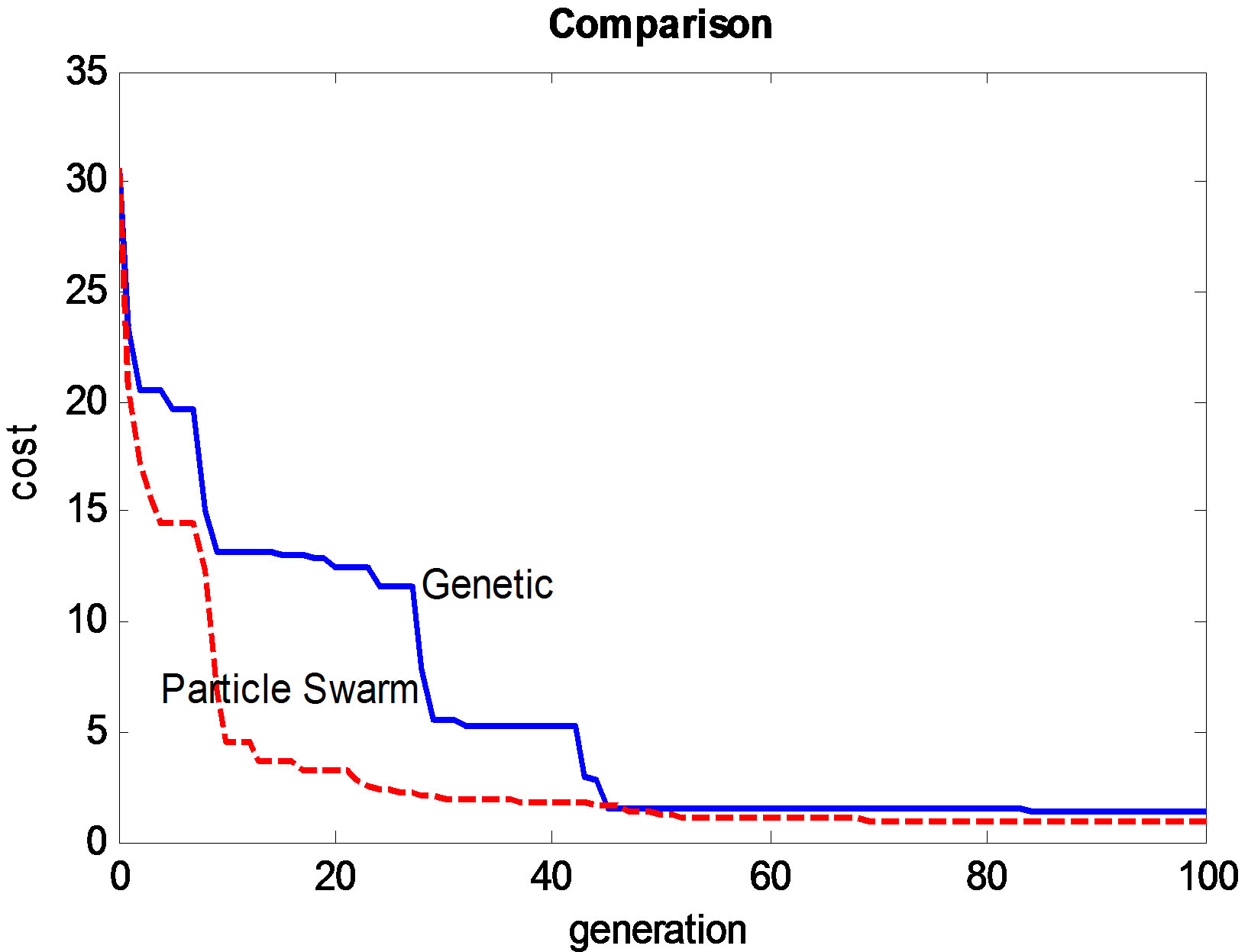
Figure 4. Convergence of the cost for PSO-based and GA-based optimization algorithms.
PID controllers. It shown empirically that the performance of the proposed method is more superior than that of existing GA due to the presence of very good speed and fitness with a few numbers of iteration and less complexity to reach the optima simulation and experimental results show the robustness and efficiency of the proposed controller. The PSO-based method can be most widely used for designing high-performance optimal controllers.
REFERENCES
- Bernstein, D.S. and Haddad, W.M. (1989) LQG control with a H∞ performance bound: A Riccati equation approach. IEEE Transactions on Automatic Control, 34, 293- 305. http://dx.doi.org/10.1109/9.16419
- Chen, B.S., Cheng, Y.M., et al. (1995) A genetic approachto mixed H2/H∞ optimal PID control. IEEE Control Systems, 15, 51-60. http://dx.doi.org/10.1109/37.466262
- Ho, S.J., Ho, S.Y., et al. (2004) OSA: Orthogonal simulated annealing algorithm and its application to designing mixed
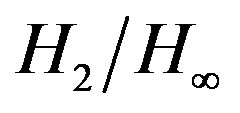 optimal controllers. IEEE Transactions on Systems, Man and Cybernetics, 34, 588-600.
optimal controllers. IEEE Transactions on Systems, Man and Cybernetics, 34, 588-600. - Kennedy, J. and Eberhart, R. (1995) Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks, 4, 1942-1948.
- Kao, C.C., Chuang, C.W., et al. (2006) The self-turning PID control in a slider-crank mechanism system by applying particle swarm optimization approach. Mechatronics, 16, 513-522. http://dx.doi.org/10.1016/j.mechatronics.2006.03.007
- Chang, W.D. (2007) PID control for chaotic synchronization using particle swarm optimization. Chaos Solitons & Fractals, 39, 910-917. http://dx.doi.org/10.1016/j.chaos.2007.01.064
- Chen, B.-S. and Cheng, Y.-M. (1998) A structure-specified
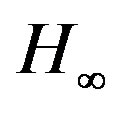 optimal control design for practical applications: A genetic approach. IEEE Transactions on Control Systems Technology, 6, 707-718. http://dx.doi.org/10.1109/87.726532
optimal control design for practical applications: A genetic approach. IEEE Transactions on Control Systems Technology, 6, 707-718. http://dx.doi.org/10.1109/87.726532 - Tan, W., Chen, T. and Marquez, H.J. (2002) Robust controller design and PID tuning for multivariable processes. Asian Journal of Control, 4, 439-451. http://dx.doi.org/10.1111/j.1934-6093.2002.tb00085.x
- Song, M.P. and Gu, G.C. (2004) Research on particle swarm optimization: A review. Proceedings of 2004 International Conference on Machine Learning and Cybernetics, Shanghai, 26-29 August 2004, 2236-2241.