Natural Science
Vol.5 No.2(2013), Article ID:27836,13 pages DOI:10.4236/ns.2013.52030
Fluid phases of argon: A debate on the absence of van der Waals’ “critical point”
![]()
Manchester Institute of Biotechnology University of Manchester, Manchester, UK; les.woodcock@manchester.ac.uk
Received 5 November 2012; revised 10 December 2012; accepted 22 December 2012
Keywords: Critical Point; Supercritical Fluids; Liquid Phase
ABSTRACT
A phase diagram of argon based upon percolation transition loci determined from literature experimental p-V isotherms, and simulation values using a Lennard-Jones model shows three fluid phases. The liquid phase spans all temperatures, from a metastable amorphous ground state at 0 K, to ultra-high T. There is a supercritical mesophase bounded by percolation transition loci, and a gas phase. Intersection of two percolation loci in the p-T plane thermodynamically defines a critical line between two coexisting gas and liquid critical states at T = Tc, and the single mesophase for T wang##Bracket# Tc. A debate on the absence of a van der Waals critical point in the Gibbs p-T density surface is appended.
1. INTRODUCTION
When van der Waals wrote his renowned thesis [1] on the theory of the liquid and gas critical point in 1873, he would not have been aware of Gibbs work on thermodynamic equilibria, also published in 1873 [2]. The van der Waals critical point does not comply with Gibbs phase rule. Its existence is based upon a hypothesis rather than a thermodynamic definition. Moreover, no one has ever succeeded in measuring a critical density of an atomic or molecular fluid directly; liquid-gas critical densities are only obtained experimentally indirectly by an extrapolation of a mean of the two coexisting densities of liquid and vapor using the law of rectilinear diameters [3]. Yet, the existence of a critical point singularity in the ρ(p,T) density surface has not been questioned until very recently [4].
Here, we present compelling evidence from experiment, simulation and theory, to show that the “critical point”, hypothesized by van der Waals, does not exist as such. Existing knowledge of percolation transitions, and consideration of existing thermodynamic properties of liquid argon from the literature are not consistent with van der Waals hypothesis, but they are entirely consistent with the concept of a “line of critical coexisting states” at Tc, i.e. the temperature above which it is impossible to liquefy a gas by the application of higher pressure.
Gibbs defined surfaces of thermodynamic state functions, and subsequently explained all 1st-order thermodynamic phase transitions. A point on the Gibbs ρ(p,T) surface can only be defined thermodynamically where two lines intersect. For example, in a single phase region, a state point with two degrees-of-freedom (F) is the intersection of an isobar and an isotherm. A state point in a two-phase region (F = 1), is the intersection of either an isotherm or an isobar with a coexistence line. There are no conceptual problems with the definition of the triplepoint; it is the intersection of the liquid-vapor coexistence line and the solid-vapor coexistence line in the p-T plane. By contrast, there is no thermodynamic definition of the “critical point” of van der Waals; indeed if at Tc (dp/dρ)T = 0, there would be one phase and one degree of freedom; a contradiction of the laws of thermodynamics by Gibbs deductions.
This conundrum has been resolved from simulation studies on hard-sphere and square-well fluid percolation transitions [4,5]; at the critical temperature there is a 2-phase coexistence line between the densities of two percolation transitions. By analogy with the triple point, Tc, pc is found to be a “double point” with a single degree of freedom in the p-T plane where the percolation transition pressure loci intersect, as shown in Figure 1 for fluid argon. At Tc, each state-point corresponds to a different density, and since (Vdp)T = dμ = 0 there is a connecting line of states at Tc, pc of constant Gibbs chemical potential (μ). Thus, the 2nd-order percolation transitions on intersection in the p-T plane, become a 1st-order phase transition, in compliance with Gibbs phase rule.
The liquid-vapor coexistence line in Figure 1 is taken from the experimental p-V-T data of Gilgen et al. [6,7] which, except in the immediate vicinity of the critical temperature, is reported with 6-figure accuracy. The data points for the two percolation transitions are obtained from the discontinuity in the slope of the p(ρ) isotherms,
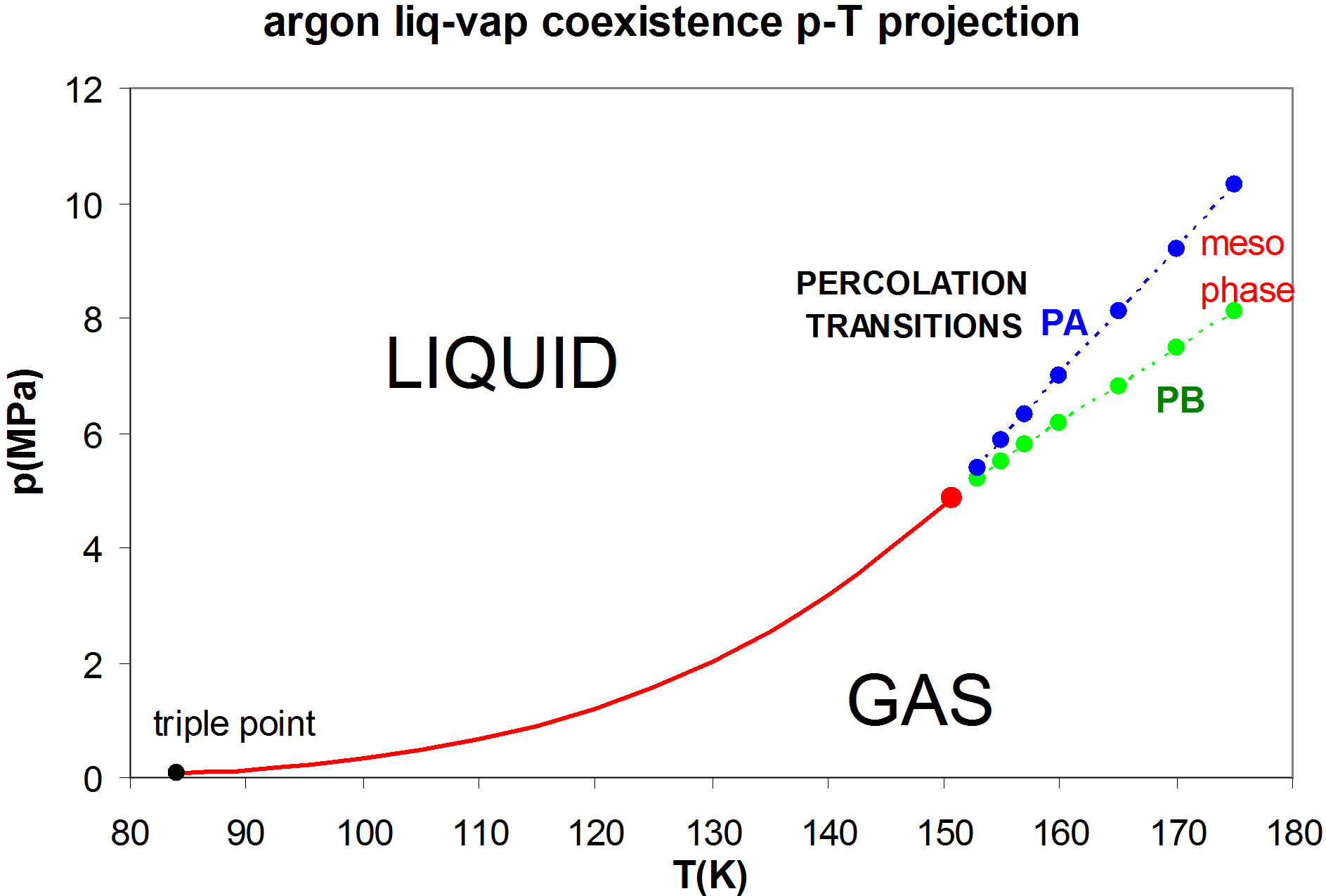
Figure 1. The liquid-vapor coexistence line for argon using the measurements of Gilgen et al. [6,7] for the coexistence line (red); PA (blue) is the available-volume percolation transition and PB (green) is the bonded-cluster percolation transition, both also obtained from the Gilgen supercritical experimental measurements [6]; the percolation transitions define the bounds of a supercritical mesophase.
for seven supercritical isotherms as shown in Figure 2. Using this information, and knowledge of the percolation transitions for the high-temperature limit of argon, if it is represented by a Lennard-Jones model, we can now obtain a reasonably accurate prediction the whole fluid phase diagram.
2. PERCOLATION TRANSITIONS
The available volume (Va) percolation transition (PA) occurs at the density (ρpa) at which the volume accessible to any single mobile atom, in static equilibrium configuration of all the other atoms, percolates the whole system. It is related to the excess Gibbs chemical potential relative to an ideal gas at the same temperature and volume (μe) by the equation
 (1)
(1)
The bonded-cluster percolation transition (PB), is the same percolation transition, previously referred to for square-well fluids [4] as the extended-volume percolation transition. Now, for real molecules we need to distinguish between the excluded volume percolation transition (PE), which is also a cluster system-spanning transition, and the bonded-cluster percolation transition (PB).
At percolation transitions, thermodynamic state functions can change form due to sudden changes in statedependence of density and/or energy fluctuations. For the hard-sphere fluid, PA is a very weak, but definite, higher-order thermodynamic phase transition [5]. Purely repulsive potential models, such as hard or soft repulsive spheres, have a gas-like region and a liquid-like region on either side of PA. The percolation transitions, as shown in Figure 1, have been computed from simulations in hard-sphere and square-well model fluids, and have been

Figure 2. Experimental data points for the p-V isotherms of supercritical argon from the tabulations of Gilgen et al. [6]. The extended straight lines, fitted in the intermediate linear region, have been superimposed to highlight the percolation transition loci shown as dashed lines. ρpb is the density of the bonded cluster percolation transition, and ρpa is the density of the available-volume percolation transition.
found to play a central role in the thermodynamic description of liquid-gas critical phenomena [4].
We do not presently know whether PE has a thermodynamic status for the hard-sphere fluid. When an attractive perturbation is added, however, both percolation transitions gain strength as temperature is reduced. This gives rise to weak 2nd-order thermodynamic phase transitions, in which there are discontinuities in second derivatives of chemical potential with respect to temperature or pressure, notably: isothermal compressibility (d2μ/dp2)T, heat capacity (d2μ/dT2)p and thermal expansivity (d2μ/ dpdT) all of which undergo some degree of change at a percolation transitions.
The bonded-cluster percolation transition (PB) occurs when atoms bonded together, within a given characteristic distance, around the minimum in the pair potential, first begins to span the system. Unlike PA, PB manifests itself more in the temperature derivatives of the chemical potential which are determined by fluctuations in the energy, rather than density. Thus we are likely to see lines of discontinuity, showing apparent maxima or minima, in the 2nd-order properties heat capacity and thermal expansivity.
3. PHASE DIAGRAM
The phase diagram in Figures 1 and 2 shows only the two percolation transitions that determine the critical coexistence. Atomic fluids have only one availablevolume percolation transition (PA), but of the other two percolation transitions, the bonded-cluster percolation transition (PB) occurs at a much higher density than the excluded volume percolation transition (PE). Thus the bonded-cluster percolation intersects the available volume percolation line first at the higher temperature and pressure to effect the first-order phase transition as shown in Figure 1. At present, we do not have information on the excluded volume percolation transition and its effect, if any, at lower temperatures, i.e. on intersecting the vapor-phase coexistence line at a temperature between Tc and the triple point.
To obtain a general simple-fluid phase diagram, we use the Lennard-Jones potential with the scalable energy (ε) and distance corresponding to the diameter of a hard sphere reference fluid where r0 is in dimension of the distance of zero force at ε = −1.
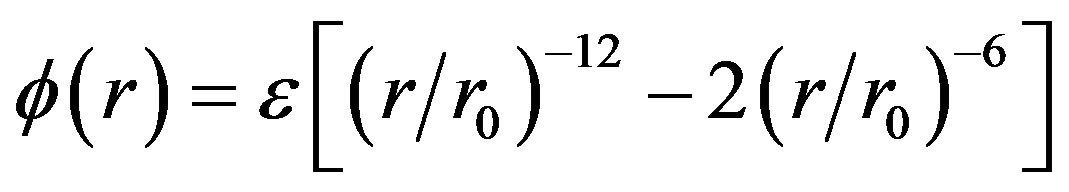 (2)
(2)
The phase diagram in Figure 3 has been constructed follows. Beginning with the raw data from the Gilgen tables [6,7], the experimental mass densities at Tc can be converted to reduced number densities for comparison with the known percolation transitions of the hard-sphere reference fluid. Using a Lennard-Jones pair potential argon take σ = 3.405 ´ 10−;10 m; then the reference hardsphere diameter corresponding to zero-force is r0 = 2(1/6) σ =3.822 ´ 1010 m; taking Avagadro’s number N = 6.0221 ´ 1023 and argon atomic mass = 39.948, the data points of Gilgen have been converted to L-J units, with reduced number density ρ = Nr03/V.
Nobody has ever measured a critical density directly [3]; this is well illustrated from the experimental measurements of the argon liquid vapor coexistence densities by Gilgen et al. [7]. The highest temperature for which they report both coexisting vapor and liquid densities is 150.61. They use the law of rectilinear diameters to obtain their “critical point” temperature 150.69, and critical density 535.6 kg/m3. The mean of the two highest recorded liquid and vapor densities is 536. The lowest coexisting liquid mass density they report is 602 kg/m3 giving ρPA(Tc) = 0.507. The highest vapor mass density they can observe near Tc is 470 kg/m3 which corresponds to ρPB = 0.395. The line of critical states connects these two points (Figures 2 and 3).
We can calculate a characteristic bond-length that defines a bonded-cluster percolation transition from the hard-sphere model, i.e. in a first-order perturbation approximation, if the structure is not perturbed significantly by the attraction. From an EXCEL power-law trendline parameterization of the extended volume percolation transition density as a function of cluster-length l from table I in the paper of Heyes et al. [8], an inversion gives
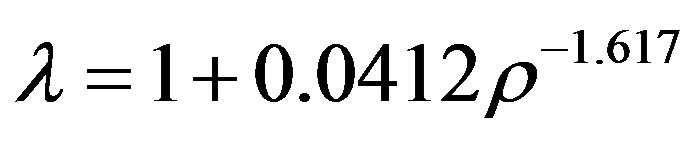 (3)
(3)
After conversion to L-J units, substituting ρ f or the minimum liquid density of Gilgen et al. at the critical temperature, we obtain lPA(Tc) = 1.185, which is in the anticipated range of the Lennard-Jones attraction; slightly greater than the distance of maximum attractive force which, from the first derivative of Eq.2, is (13/7)1/6 = 1.1086.
To complete the construction of the phase diagram (Figure 3) we need the two percolation densities ρPE and ρPA of the soft-sphere fluid which is the high-temperature limit of the L-J fluid. The density of PE for purely repulsive soft-spheres ρPE(ss) = 0.085 is obtained from Heyes et al. [8]. The density of the softsphere available volume percolation density ρPA(ss) = 0.48 is determined in reference [9]. The equilibrium fluid freezing density of the high-temperature limit is obtained from Hoover et al. for the soft-sphere model [10], ρf(ss) = 1.51. These three phase transition points are the limiting high-temperature bounds of argon’s three fluid phases at β = ε/kBT = 0 in Figure 3.
The bonded cluster percolation transition clearly must become increasingly weaker with temperature and eventually non-existent, probably before it crosses the excluded volume percolation transition at the much lower density. Likewise, it is not presently known what the extent and manifestations of the excluded volume percolation transition (PE) in Figure 3 are at low temperatures. There is the possibility of a second mesophase bounded by PE and PB.
4. SUPERCRITICAL MESOPHASE
From the general picture in Figure 3, we can summarize the thermophysics of the liquid state. First, since a

Figure 3. Phase diagram of argon, excluding crystalline phases, reduced to Lennard-Jones units; the red dots show the coexisting densities from the experimental measurements of Gilgen et al. [6,7]; the densities of the soft-sphere percolation transitions PE and PA in the high-temperature limit (β = 0), and the soft-sphere freezing density (black dot) are obtained from references [8-10] respectively.
thermodynamic phase equation-of-state is continuous in all derivatives, within the F = 2 Gibbs region of a phase diagram, the coexistence line will extend all the way from T = 0 at an amorphous ground state (ρa). For argon at T à 0K and vanishing pressures, this should be close to the random close-packed density of the hard-sphere fluid ρrcp = 1.216 [4]. The critical temperature (Tc) now has a thermodynamic definition; by the intersection of the available-volume and the bonded-cluster percolation transitions. In the p-T projection of the ρ(p,T) Gibbs surface, these two lines intersect to trigger a first-order phase transition whereupon the gas at density ρPB and liquid at density ρPA coexist. The liquid phase extends all the way from 0K to an essentially-infinite temperature for a fluid defined by a classical model Hamiltonian, albeit metastable below the triple point temperature.
Brazhkin et al. [11] have calculated the values Cp, αp, and a “Widom line” (related to κT) for several isotherms of the Lennard-Jones supercritical fluid. These authors are unaware of the role of percolation transitions, but an inspection of their results is entirely consistent with the present thermodynamic based description. First, Cp against pressure, in Figure 3(a) of reference [11], shows a pronounced discontinuity at the reduced pressure pσ3/ε = 0.2 (note: σ = r0/2(1/6)) for the lowest isotherm T/Tc = 1.4. Second ap isotherms in Figure 2(b) of reference [11] have flat maxima roughly spanning the two percolation densities shown here in Figures 2 and 3. The isothermal compressibility (κT) increases monotonically from ideal gas to dense liquid, but when multiplied by a “correlation length”, that decreases monotonically from ideal gas to dense liquid, the resulting maximum locus, which has been called the Widom line, seems to lie broadly within the two percolation densities ρPA and ρPB as seen in Figure 4 of reference [11].
Percolation transitions are known to be associated with discontinuities in linear and nonlinear transport properties [12-14], and various other dynamical properties such
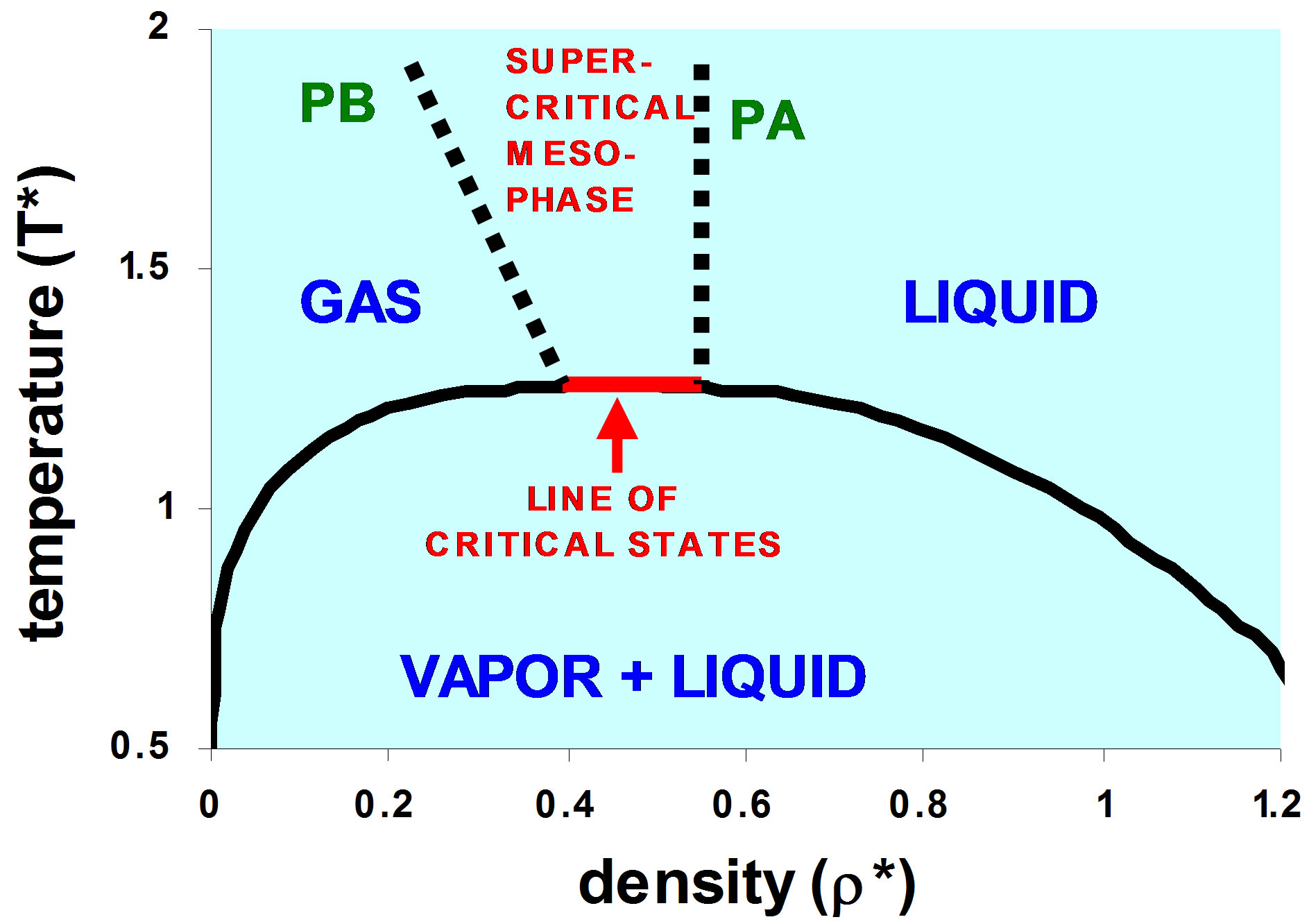
Figure 4. Schematic picture of the phase diagram for a simple fluid such as argon.
as frequency spectra [12]. There is an increasing literature [13] of hitherto “inexplicable” supercritical lines associated with observations of changes in dynamical properties from gas-like to liquid-like in various supercritical fluids, including water. It seems likely a simple thermodynamic explanation for the existence of all these lines will be forthcoming when the percolation transition loci in these fluids are investigated. Interestingly, the little graphic presented within the abstract of the paper of Brazhkin et al. [11], shows all three lines of maxima stemming from the critical point in the p-T plane. All of their lines can be identified with the present thermodynamic percolation transition loci, shown here in Figure 1 also in the p-T plane. Their ζ(T)-max locus is near PB, their Cp-max locus is near PA, and their ap-max locus is intermediate between PA and PB loci. A discontinuity locus referred to by Brazhkin et al. [11] as a “Widom line” can actually be seen in Figure 9 of the paper by Heyes and Melrose, published 25 years ago, which they identified as the line a percolation transition [14].
5. CONCLUSIONS
The previous conclusion [4] that real liquids behave in a similar way to the square-well model fluids in that there is a line of critical coexistence states being a twophase system of a liquid and vapor is reaffirmed. At the critical temperature, there is a range of volumes between the maximum gas coexisting density, and the minimum liquid coexisting density for which the two-phase separation disappears. There is no van der Waals “critical point” on the Gibbs density surface as illustrated in Figure 4.
For temperatures above Tc there exists a superctitical mesophase bounded by percolation transitions of occupied and available volumes (clusters of sites and holes) or PB and PA respectively. In this region the pressure isotherms are linear functions of density, indicating a supercritical extension of the Lever rule, whereby a single phase consists of a fluctuating mixture of gas-like cluster distributions, and single system-spanning liquidlike clusters, with a linear combination of the percolation pressures at the respective densities ρpb and ρpa.
For temperatures below Tc, at thermodynamic equilibrium, there is the familiar two-phase coexistence region. The percolation loci PB and PA, however, over the entire temperature range, bound the gas and liquid phases, respectively. It is suggested that below the line of critical states, in the two-phase region, the loci of PB and PA will connect with the metastable limits of gas and liquid respectively, i.e. non-equilibrium spinodal decomposition lines, between metastable and unstable state points in the otherwise two-phase region.
The van der Waals theory of a critical point [1], for which he received the Nobel prize in 1910 [15], has been universally accepted description of liquid-gas criticality ever since.
According to this hypothesis, every fluid has an equation-of-state for which the first two derivatives of pressure with respect to changes in density or volume, go to zero at a singular point on the Gibbs density surface. A second misapprehension that has been in fashion for 50 years, a concept to describe all critical phenomena, from Ising models, ferro-magnetic systems, spin glasses add liquid-gas criticality, is “universality”. All critical phenomena, according to this theoretical physics community, obey the same universal physical description, which has been explained, culminating in a second Nobel prize being awarded in 1982 to Wilson [16] for his application of renormalization group theory to the generalization of critical points descriptions including the hypothetical van der Waals “critical point” singularity.
After 140 years of scientific investigation, how could the physics community get the science so completely wrong, when all the essential experimental data, and some theory, has been out there all along?
Some clues to the answer to this question can be found in the Nobel addresses: van der Waals had problems with critical volumes, he refers throughout his Nobel lecture [15] to “the critical volume”, but nowhere does say that its existence is a hypothesis; i.e. it is very misleading. At one stage, however, he states: “…and again it can be seen from the equation that what I have termed the weak point of my theory is actually responsible for the theoretical impossibility of calculating accurately the critical volume”. In fact, it is the incorrect hypothesized mathematical form of the equation-of-state of superctritical fluids, with a cubic node, that generates the spurious “critical point”.
Wilson, in the introduction to his Nobel address [16], summarizes the phenomenology of liquid-gas criticality by reference to water and steam in one brief paragraph as follows: “A critical point is a special example of a phase transition. Consider, e.g. the water-steam transition. Suppose the water and steam are placed under pressure, always at the boiling temperature. At the critical point, the distinction between water and steam disappears, and the whole boiling phenomena vanishes. The principal distinction between water and steam is that they have different densities. As the pressure and temperature approach their critical values the difference in density between water and steam goes to zero”. This statement is the only reference to any liquid-gas experimental coexistence data in the entire lecture. There is no reference at all to the Gibbs classical thermodynamic description, in a 32-page Nobel lecture. In fact, liquid-gas criticality is not mentioned again! We now see that the experimental phenomenology on which Wilson’s theory, and indeed also the Nobel prize, is to a large extent, justified, is quite incorrect.
Notwithstanding two Nobel prizes in physics for theory of a “critical point” that does not exist, we conjecture that the present description of liquid-gas criticality of argon will be the same phenomenology for all liquids. The density difference between water and steam is the same phenomenology as “fluid phases of argon”, it does not go to zero at the critical temperature. [17]. Moreover, for temperatures above the critical temperature the gas and liquid phases of water and steam are separated by a supercritical mesophase (referred to as steam II [17]) which is a homogeneous mixture of gas-like small clusters, and system spanning large clusters, all with the same Gibbs chemical potential. These phase boundaries appear as a weak second-order thermodynamic phase transition, referred to as percolation transition loci [17], not presently well understood at the molecular level, but now requiring further experimental and theoretical investigation.
6. ACKNOWLEDGEMENTS
I wish to thank colleagues Dr. John F. Maguire and Dr. Frank van Swol of Scientific Simulation Systems Inc. for encouraging discussions, and Prof. David M. Heyes of Imperial College London for many helpful contributions from his work on percolation transitions, and for information from his hitherto unpublished results for the Lennard-Jones fluid which reaffirm the conclusions expressed in this paper.
REFERENCES
- Van der Waals, J.D. (1873) Over de continuiteit van den gas-en vloeistoftoestand (on the continuity of the gas and liquid state). Ph.D. Thesis, University of Amsterdam, Amsterdam.
- Gibbs, J.W. (1873) A method of geometrical representation of the thermodynamic properties of substances by means of surfaces. Transactions of the Connecticut Academy of Arts and Sciences, 2, 382-404.
- Reif-Acherman, S. (2010) History of the law of rectilinear diameters. Quimica Nova, 33, 2003-2013. doi:10.1590/S0100-40422010000900033
- Woodcock, L.V. (2012) Thermodynamic description of liquid-state limits. The Journal of Physical Chemistry B, 116, 3734-3744. doi:10.1021/jp2116214
- Woodcock, L.V. (2011) Percolation transitions in the hard-sphere fluid. AIChE Journal, 58, 1610-1618. doi:10.1002/aic.12666
- Gilgen, R., Kleinrahm, R. and Wagner, W. (1994) Measurement and correlation of the (pressure, density, temperature) relation of argon: I the homogeneous gas and liquid regions in the temperature range from 90K to 340K at pressures up to 12 MPa. The Journal of Chemical Thermodynamics, 26, 383-398. doi:10.1006/jcht.1994.1048
- Gilgen, R., Kleinrahm, R. and Wagner, W. (1994) Measurement and correlation of the (pressure, density, temperature) relation of argon: II saturated-liquid and saturated vapor densities and vapor pressures along the entire coexistence curve. The Journal of Chemical Thermodynamics, 26, 399-413. doi:10.1006/jcht.1994.1049
- Heyes, D.M., Cass, M. and Branka, A.C. (2006) Percolation threshold of hard-sphere fluids in between the softcore and hard-core limits. Molecular Physics, 104, 3137- 3146. doi:10.1080/00268970600997721
- Woodcock, L.V. (1987) Developments in the non-Newtonian rheology of glass forming liquids. Lecture Notes in Physics, Springer-Verlag, 277, 113-123.
- Hoover, W.G., Ross, M.K., Johnson, W., Henderson, D., Barker, J.A. and Brown, E.C. (1970) Soft-sphere equations of state. Journal of Chemical Physics, 52, 4931- 4936.
- Brazhkin, V.V., Fomin, Y.-D., Lyapin, A.G., Ryzhov, V. N. and Tsiok, E.N. (2011) Widom line for the liquid-gas transition in Lennard-Jones system. The Journal of Physical Chemistry B, 115, 14112-14115. doi:10.1021/jp2039898
- Brazhkin, V.V., Fomin, Y.-D., Lyapin, A.G., Ryzhov, V.N. and Trachenco, K. (2012) Two liquid states of matter: A dynamic line on a phase diagram. Physical Review E, 85, 03120. doi:10.1103/PhysRevE.85.031203
- McMillan, P.F. and Stanley, H.E. (2010) Going supercritical. Nature Physics, 6, 479-480. doi:10.1038/nphys1711
- Heyes, D.M. and Melrose, J.R. (1989) Microscopic simulation of rheology: Molecular dynamics computations and percolation theory. Molecular Simulation, 2, 281-300. doi:10.1080/08927028908034606
- Van der Waals, J.D. (1967) The equation of state for gases and liquids. 12 December 1910, Nobel Lectures, Physics 1901-1921, Elsevier Publishing Company, Amsterdam.
- Wilson, K.G. (1993) The renormalization group and critical phenomena. 8 December 1982, Nobel Lectures, Physics 1981-1990, In: G. Ekspång, Ed., World Scientific Publishing Co., Singapore.
- Woodcock, L.V. (2012) Observations of a thermodynamic liquid-gas critical coexistence line and supercritical fluid phase bounds from percolation transition loci. Fluid Phase Equilibria, in Press. doi:10.1016/j.fluid.2012.08.029
- APPENDIX
Debate on the Absence of a Van Der Waals Critical Point in the Gibbs p-T Density Surface
An original paper titled “Fluid phases of argon” [A1] was submitted to Physical Review Letters (PRL) for publication. The paper was not recommended for publiccation on the basis of adverse and critical comments of disbelief by three anonymous referees [A2]. In the interests of innovation, there should be an open debate on the scientific issues. Here we reproduce the debate on the adverse viewpoints put forward these anonymous referees. The referees’ reports were unreservedly supported by a PRL Divisional Associate Editor (DAE) [A3] and further re-enforced by a second PRL DAE [A4].
The first anonymous referee (A) said this paper is not suitable for publication because a statement upon which it is partly based, i.e. that “van der Waals critical point does not comply with Gibbs phase rule ...” is incorrect. Referee A argued, “if the phase rule is used correctly: F = C − P + 2 − R, where R is the number of additional constraints, i.e., constraints not implied by the conditions of phase equilibrium, constraints imposed by chemical equilibrium. Another example are critical points, at which one would require 2 derivatives (dp/dV, d2p/dV) to vanish. So the critical point complies with the phase rule after all.”
The generalization of Gibb’s phase rule F= (C − R) − P + 2 is only applicable to multi-component systems in which the number of independent chemical components (C − R) is reduced by the number of chemical equilibria constraints e.g. chemical reactions, or azeotropes. It is not applicable to a one component system. There is no thermodynamic definition of the hypothetical “critical point”; such a singular point, with (dp/dV = 0), would be thermodynamically unstable. The referee’s use of the expression “the critical point” indicates prejudice.
Referee A continued with his criticism of another statement in the same paragraph, i.e. that “... critical densities are only obtained experimentally indirectly ... Why indirectly, referee A asked? One fills a variable-volume cell with the liquid, slowly increases temperature, and manipulates the volume to keep the meniscus in the middle of the cell. When the meniscus vanishes (or critical opalescence sets in), the cell volume corresponds to the critical volume.”
This statement presupposes the hypothetical existence of “the critical point” again, indicating prejudice. Indeed, this is exactly what one would expect to see at the transition from two-phases to one; when the meniscus vanishes, or critical opalescence sets in, the cell volume corresponds to the mean coexistence volume of liquid and vapor states, at the critical temperature. The range of volumes for which the meniscus disappears at the same temperature is a well known established experimental fact for many decades; see Mayer and Mayer: Statistical Mechanics 1940 p. 313 last paragraph.
Referee A went on to say that “Gilgen et al. used the rectilinear diameter extrapolation to construct a good engineering equation of state, but that should not be taken as a proof that everybody has to follow their example. Moreover, precise measurements (especially from the Wagner group) have shown that the law of the rectilinear diameter is not quite true.
The Gilgen data on argon, however, has not been taken to “prove” anything. The law of rectilinear diameters, with various subtle modifications, has a long history of use, to enable prediction of a singular “critical volume” which does not exist.
Referee A continued: “A state point in the two-phase region (F = 1) is the intersection of either an isotherm or an isobar with a coexistence line. Why ‘either’? Sometimes we have to use intersections with isochores or other thermodynamic curves.”
This is an irrelevant point by referee A; of course this statements applies to other Gibbs surfaces e.g. T, density surfaces; the sentence reviewer A actually quotes from begins with the words “For example,… etc.” the comment is therefore irrelevant.
Referee A then turned to Figure 3 “the fact that the measurements of the Wagner group stopped short of the critical point has something to do with the design of their apparatus. Many experiments have been reported, e.g., by the group of Jan. V. Sengers, with other apparatus in the immediate vicinity of critical points, usually with the objective to measure critical exponents, and these experiments usually did not mention gaps in their phase envelopes.”
The statement that no one has previously directly measured a critical point density is correct; see e.g. S. Reif-Acherman History of the Law of Rectilinear Diameters . Can this referee supply a reference(s) to “report of Jan V. Sengers”, or “many experiments”?
Referee A then said that, overall, there seems to be a problem with nomenclature. It is a bad habit of theoreticcal physicists to call zeros of thermodynamic derivatives “phase transitions”, and if no phase separation occurs, “higher-order phase transitions”. In reality, changes of thermodynamic and transport properties in the supercritical region are continuous—if the common definition of the critical point is used.
What are “zeros of thermodynamic derivatives”? n-th order phase transitions are defined by discontinuities in an n-th derivative of Gibbs free energy with respect to one or both state variables p and T. There is “no common definition of the liquid-gas critical point; it’s existence and thermodynamic description is a hypothesis! What is a “common definition of the critical point”, we ask?
Referee A: “I doubt whether the critical point of a real fluid can be identified with an intersection point of some percolation lines could be proven. Percolation theory is working well for lattice models, but becomes rather fuzzy for molecular fluids with realistic interaction potentials.”
There can be no “proof” in a mathematical sense; thermodynamics is an empirical science! This paper shows that a line of critical states is consistent with 1) principles of Gibbs chemical thermodynamics which are rigorously derived from the 1st and 2nd laws of thermodynamics 2) experiment measurements of liquid-vapor coexistence densities and the law of rectilinear diameter going back 140 years, and 3) all previous computer simulation determinations of square-well fluid, and Lennard-Jones fluid mean critical densities.
Referee A finally said “the author should be encouraged to investigate the percolation behavior of nearcritical fluids, but the present manuscript needs more work before it is publishable.”
Referee A here admits that this description of liquid-gas criticality in liquid argon is “publishable” but has cynically sought to obstruct its publication in this final statement! All Referee A comments are based upon a preconception (and misapprehension) that the van der Waals hypothetical critical point is established scientific fact. Of course there needs to be further investigation of all the mysterious supercritical lines [8-12]. That is precisely why it is important to publish this paper now, so interested scientists can extend these new lines of research. How could one person possibly undertake all the new experimental, simulation and also theoretical physics research that this description of liquid-gas criticality now needs?
A second referee (B) (8th June 2012) reported : “ In this manuscript, Woodcock makes a series of extraordinary claims, culminating to the suggestion that there is no critical point for the vapor-liquid phase transition in argon (Figures 2 and 3). He finds a different critical density for the liquid and the gas. This is all supposedly based on experimental data of Gilgen et al. measured in 1994, which, according to Woodcock, show “discontinuity in the slope of the p(ρ) isotherms” This discontinuity exists only in the imagination of the author (see Figure 2 and the original paper of Gilgen et al.)”.
Referee B added “The whole derivation is based on the premise of the existence of these ‘second order transitions’ in argon with no explanation as to why no previous researcher has discovered their existence.”
Referee B completely overlooks the determination and characterization of the percolation transitions in the hard-sphere, soft-sphere, square-well and Lennard-Jones models [4,5,8,14] that is already out there in the literature. It is not “imagination”! The data plotted in Figure 2 is the original, 6-figure accurate, data taken numerically and directly from the tables of Gilgen et al. The breaks in (dp/dρ)T are clearly discernible, exactly where one expect to find them, and there for all to see.
Not one valid reason was given by PRL referees A and B for rejection of this paper that withstands scrutiny as grounds to obstruct the publication. Moreover, the terse commentary of referee B is inadequate, unscientific, and unprofessional. PRL were requested to obtain an alternative and less bigoted report in lieu of B.
A third report was obtained 3 months after the original submission: referee C reported “In this manuscript, the author presents the hypothesis that there is no critical point in argon and other simple fluids that can be described by the Lennard-Jones model pair potential, but instead that there is a “double point”, which in a temperature vs. density plot of the phase diagram, corresponds to a line of critical states. This claim goes against everything that is taught in all the standard text book on the subject (I list a selection below).
1) “Theory of Simple Liquids”, J.-P. Hansen and I.R. McDonald.
2) “Statistical Physics”, L.D. Landau and E.M. Lifshitz (Vol. 5 of their course on theoretical physics).
3) Principles of Condensed Matter Physics, P.M. Chaikin and T.C. Lubensky.
4) A Modern Course in Statistical Physics, L.E. Reich The above bigoted statement regarding the content of this paper is a false premise; there is no new “hypothesis”. Rather, we provide further evidence from computer simulations of percolation loci, alongside experimental isotherms, that refutes an existing “hypothesis” proposed by van der Waals 140 years ago that has been accepted but unsubstantiated ever since. We have no new theory or hypothesis; the present, alternative, interpretation of thermodynamic properties contends the van der Waals hypothesis is an incorrect conjecture, and therefore cannot be substantiated.
This statement, moreover, shows that PRL referee C does not understand what scientific research is about! The objective of research is not to rediscover what is already in text books. Instead of saying “look at the text books”, were he up to the task of reviewing this article properly, he would look at the new science and not the history books. In fact, all these four UG physics teaching books, in dealing with liquid-gas criticality, assume van der Waals conjecture of the existence of a critical point to be established science, whereas it has always remained an unsubstantiated hypothesis. All four of these text books cited by referee C incorrectly assume the hypothesis to have been established, as, of course, do many other teaching texts.
In response to this list by Referee C; we can cite four more text books, written by distinguished scientists, namely, Mayer, Ziman, Hildebrand and Gibbs.
1) “Statistical Mechanics”, Mayer and Mayer, 1st Edition, Chapter 14 (Condensation) section (i) (The Physical Interpretation of the Critical Temperature) {NB Mayer and Mayer use Tm for critical temperature, i.e. the temperature at which the meniscus appears/disappears}. Quote: page 313 last paragraph “The temperature Tm is the temperature at which the sharp meniscus separating the liquid from the gaseous phase will disappear in a system heated at constant volume v between two volumes Vg (gas) and Vl (saturated liquid). It is well known that the disappearance of the meniscus can be observed for a range of volumes and is a phenomena not limited to the single volume Vc as would be demanded by a p-V diagram such as the van der Waals equation predicts. … There is considerable other evidence for the existence of this critical region… experimental evidence indicates that the volume difference between Vg and Vl at Tm is 10% to 20% for some materials.”
2) “Models of disorder: the theoretical physics of homogeneously disordered systems J.M. Ziman 1979 Chapter 6: Thermodynamics of topological disorder” section 6.2 the van der Waals approximation: Quote: page 219, 2nd paragraph “It must be emphasized that the parallelism, between liquid-gas and Ising ferromagnetic criticality, does not imply that we have deduced from first principles a general theory of condensation of disordered fluids. The van der Waals equation itself is, frankly, phenomenological; if it did not in fact describe the behavior of real fluids, there would be little reason to accept it”.
3) “The solubility of Non-electrolytes” J.H. Hildebrand and R.L. Scott: Quote: page 461 last paragraph “A horizontal portion of the coexistence curve is probable at Tc; above this temperature, however, the activity (pressure) curves must show a finite although possibly very small, slope at all concentrations. Such a situation is shown schematically in Figure 5. It is impossible to prove experimentally that there is an absolute horizontal portion to any curve, as it is equally impossible to exclude the possibility of a small horizontal section.”
4) “Equilibrium of Heterogeneous substances” J.W. Gibbs. (Volume 1 Scientific Papers) Page 129 “Critical phases” Quote: “It has been ascertained by experiment that the variation of two coexistent states (phases) of the same substance are in some cases limited in one direction by a terminal state (phase) at which the distinction of the coexistent states (phases) vanishes… (aljebra)… in this respect, a critical phase resembles any phase which has a coexistent phase... for as every stable phase which has a coexistent phase lies upon the limit which separates stable from unstable phases, the same must be true of any stable critical phase” (i.e. the critical phase boundary is a line of critical states).
Referee C went on: “evidence that the author presents to back up his assertion is that the experimental isotherms form Gilgen et al., displayed in Figure 2 look flat near the critical density. This does not in any way prove the claim. Regular theories of the critical point also have flat looking isotherms near the critical point.”
Referee C, however, is turning scientific protocol upside down! If an observer claims to have seen a teapot in orbit between the earth and the moon, it is not up to a scientist to “prove” it doesn’t exist, it is up to the hypothesizer to substantiate his hypothesis by providing experimental evidence. Again, we can only repeat what is stated above; there has been no experimental evidence in the literature on liquid-gas coexistence density measurements, over a period of 140 years, to substantiate the hypothetical existence of a critical point as theorized and parameterized by van der Waals. Quite the contrary, the Gilgen experimental isotherms are redrawn for this paper to show that they are consistent with the discontinuities in the second derivative of chemical potential at the loci of the percolation transitions in the supercritical region shown. The Gilgen data show that at the critical temperature Tc the percolation transitions have the same pressure, and hence same chemical potential.
Referee C then expressed his disbelief at th existence of percolation loci: “the other aspect of this paper concerns the percolation lines that are presented. However, these are not well defined: One can define the effective particle radius to be almost any value one likes and so locate the percolation line wherever one wants. This is not evidence for a new critical scenario! In short, there is nothing in this paper worth publishing. It should not be published anywhere, and certainly not in PRL.”
Percolation loci are defined phenomenologically by discontinuities in the second or higher derivatives of the Gibbs chemical potential with respect to the state variables temperature or pressure, and determined experimentally. Whilst the underlying statistical Mayer cluster theory is not fully developed yet, and presently a matter of priority research, the determination of, or theoretical prescription for, characteristic distances for percolation loci, are in place, and are well-defined in the case of model square-well fluids described in reference .
A formal complaint of prejudice and bigotry resulted in an appeal to PRL Divisional Associate Editor (appointed by PRL Senior Editor Throwe) DAE J. Beamish wrote :
“Your appeal concerning the paper ‘Fluid phase of argon’ was directed to me by the editors of Physical Review Letters. I have carefully read this paper and a number of relevant works, including several of the papers which you cited. I have also read the reports of the three referees to you, the comments of the referees to the editors, and the correspondence between you and the editors. After examining the files and becoming aware of the identities and backgrounds of the referees, I cannot possibly overturn their recommendations. The editors received reports from three referees who were properly chosen as reviewers of your paper—they have extensive experience in the fields related to your submission. It is very important to appreciate that for a paper to be accepted by Physical Review Letters the editors look for referee reports that are strongly in favor of publication. In their reviews none of the referees recommends publication, nor do they suggest that a revised version would be publishable in Physical Review Letters. I have no reason to believe that the referees have any non-scientific reason to hold up publication of your article, and I have to accept that their opinions and the decision of the editors are sincere and honorable.”
Like any appeal Judge in an unbiased system of natural justice, it is surely the duty of DAE arbiter to reach a decision on the validity of scientific arguments on both sides, without prejudice, and to proffer a judgment of the validity of these scientific arguments, together with reasons for that judgment.
This brief letter-of-dismissal of the appeal tells us nothing about the judgment regarding the scientific dispute leading to the rejection of this paper. In the first paragraph of the “letter-of-judgment”, Beamish claims to have read the relevant papers referenced in the PRl [4,5]. Is it his judgment that the discovery of a “line of critical states” with its origins in percolation loci, in reference 4 does not exist? Is it his judgment that the calculations leading to the determination of the percolation transitions, which lead to the conclusions in reference 4 are somehow flawed. What is his judgment on the science?
The second part is a quite astonishing admission that his judgment has been subjective, and based not upon any scientific arguments supplied by the referees, but by the referees’ “identities”. Surely, it is the duty of a DAE arbitrator to put subjective politics aside, and judge the case on the pros and cons of scientific arguments, not the names of “anonymous” referees. We quote Max Planck who experienced similar problems. “An important scientific innovation rarely makes its way by gradually winning over and converting its opponents. What does happen is that its opponents gradually die out and that the growing generation is familiarized with the ideas from the beginning.”
Max Planck: Scientific Autobiography and Other Papers, trans. F. Gaynor (1950), 97; quoted in David L. Hull, Science as a Process (1990), 379.
Of the three referees A, B, and C, only one of them (referee A) provides any cogent scientific counterpoints. Referee A says van der Waals critical point is consistent with Gibbs phase rule. What is the DAE’s judgment and why? Referee A says that critical densities can and have been measured directly (though he has failed to produce one single reference from 140 years of experimental investigations, as we have requested); such a measurement has never existed. What is the DAE’s judgment and why?
Senior PRL Editor Throwe declined to obtain an answer from DAE Beamish, but, instead, obtained a second report on rebuttals from referee A which began by again questioning the non-compliance of van der Waals with Gibbs phase rule. Referee A said: “Gibbs’ phase rule merely compares the number of variables and the number of equations, conditions, or constraints. There is no reason why “constraints” should be limited to chemical equilibria. E.g., for vapor-liquid equilibria of mixtures, azeotropy can be a legal (non-chemical) constraint. So-called pure substances are in reality mixtures of several nuclidic species with fixed mole fraction ratios; so we have a stoichiometric constraint here.”
The first of these revised statements by referee A is not relevant to a one-component fluid. This second statement begs the question: what is the “stoichiometric constraint” at van der Waals hypothetical critical point of a simple fluid like argon?
Referee A said “A thermodynamic state with dp/dV = 0 is not unstable, it is at the border of instability.”
This is yet another nonsensical statement! All thermodynamic state points on a Gibbs surface, in the thermodynamic limit, are, by definition, stable. The state point hypothesized by van der Waals would be unstable according to Gibbs’ criteria. One can of course have metastable states of a single phase in a two phase region.
Referee A added further criticism: “The classical thermodynamic definition of a pure fluid critical point is either an inflection point with a horizontal tangent on an isotherm in a p-V diagram (i.e., a single-phase state with 2 constraints) or the point of maximal pressure up to which a vapor-liquid equilibrium occurs (two-phase state with 1 constraint). Whichever definition is preferred, there are constraints, and the number of degrees of freedom at the critical point is zero.” A modern textbook discussing such matters is: U.K. Deiters and Th. Kraska, High-Pressure Fluid Phase Equilibria-Phenomenology and Computation, Elsevier, Amsterdam 2012.
Referee A does not understand the “point” (no pun intended). These are not “thermodynamic definitions”, but hypotheses regarding the form of the p(V,T) thermodynamic equations-of-state. Again, I maintain that there is no “thermodynamic definition” of van der Waals critical point. The textbook cited does not discuss this question, nor does it give any research references. The book incorrectly states that in Gibbs phase rule the number of degrees-of-freedom at a liquid-gas critical point is zero because there are two constraints arising from van der Waals hypothesis that dp/dV = 0 and d2p/dV2 = 0. These are not thermodynamic constraints, and have nothing to do with the definition of state points on the Gibbs p-T density surface. There is still no reference, neither in the original report of refere A, nor in the response to my request in my first rebuttal, and not in this book he now cites, i.e. to the argument found on page 7; nowhere in that book is there a research reference to this argumentof referee A.
By contrast, I will supply an original reference that shows that, at the critical temperature, it is not just the first two derivatives that are equal to zero, all the derivatives of p with respect to V go to zero as slope of the p(ρ) isotherm in the supercritical mesophase, which so far, has invariable been found to be linear, goes to zero. Hence at this temperature the critical phases referred to by Gibbs , lie on a horizontal straight line. The reference is Bruno H. Zimm,“Contributions to the theory of critical phenomena”, Journal of Chemical Physics Vol. 19 pp. 1019-1023 (1951). Quote: “If one considers the critical point between the liquid and gaseous phases, it may be shown that the ‘principle of superposition’ leads to the result that the critical point is a singularity in the isotherm of fugacity or pressure against density. At this singularity the derivatives of every order of the fugacity or pressure with respect to the density are zero, not only the first two derivatives as in the van der Waals theory.”
Referee A turned again to measurement of critical volumes: “Of course the described experiment primarily gives mean volumes. If one does not believe in the existence of a single critical point, it does not make sense to define a critical volume. But this would only be true if the author’s hypothesis were correct, and this has still to be proven. The range of the volumes for which the meniscus disappears has shrunk over the past decades as a consequence of apparatus design improvements; it does not seem to be a physical parameter for each fluid.”
The hypothesis that needs to be substantiated, however, is that of van der Waals; that there exists a critical point singularity on the Gibbs density surface. Despite a very clear request in the original rebuttal, PRL Referee A has failed to provide one single reference from the tens of thousands of experimental papers over a period of 140 years that could substantiate the singular critical density hypothesis.
Referee A further said that “in measurement of Vmc the law of rectilinear diameters is not the only way to determine critical densities. Cailletet apparatus measurements are an alternative, or light scattering. The author should look at Johanna M. H. Levelt Sengers “How Fluids Unmix”, Edita KNAW, Amsterdam, for a historical overview of fluid criticality, which also cites some key experimental publications.
On reading this review by Mrs. J.V. Sengers, whose husband is the one person in 140 years, who referee A claims to have directly measured a critical point. Nowhere in the references of that review can I find reference to any paper that directly observes a critical point density, by any method that withstands scrutiny. Moreover, the reason Referee A cannot supply a “thermodynamic definition” of van der Waals “critical point” because there is no such definition.
Referee A then became philosophical: “the formalism of classical thermodynamics is isomorphic with Euclidean geometry (F. Weinhold, Physics Today, March 1976, 23-30). The line of critical points is merely a vapor-liquid coexistence line, and such is indeed compatible with Gibbs’ thermodynamics. But along such a line, compression requires work, and one cannot have the well-established divergence of fluctuations. I am afraid that the author’s view is not compatible with reality.”
Of course there will be thermodynamic descriptive analogies with Euclidean geometry of Gibbs surfaces, this has been known since the work of Gibbs himself, and later discussed by the work of J.C. Maxwell 100 years before Weinhold! This statement is not relevant to the present scientific debate. Regarding the line of critical states, its quite the contrary, it is the divergence of fluctuations as the pressures of the two percolation transitions become the same and dp/dρ à 0 that triggers the first-order phase transition and the existence of a critical line as T is reduced to Tc (or vice versa as T is increased to Tc). What is not compatible with reality is van der Waals hypothesis.
Referee A continued: “I am not aware of any experiment or simulation excluding the existence of a critical “point” in fluids. Moreover, a new theory to replace the present view of critical phenomena should also explain why renormalization group theory (which evidently requires the existence of a singular critical point) works.”
Reviewer A, like referee C, is now turning scientific protocol upside down! It is not up to me to find an experiment that shows van der Waals critical point does not exist. It is surely incumbent upon believers in van der Waals hypothesis to provide reproducible experimental evidence, notwithstanding the vast literature in theoreticcal physics and two Nobel prizes ([15,16] see conclusions), to show that it does! In 140 years since van der Waals, nobody has yet achieved this very clear objective! The reason is that the critical point envisioned by van der Waals cannot exist as such.
Referee A in summary said “I am not cynical. I merely check whether a manuscript is faulty, incomplete, or incomprehensible. Perhaps I am sometimes too polite when I formulate my opinion. I do not mind passing manuscripts containing unusual or exotic theories. But the present manuscript misinterprets or simply ignores older literature. This is why I still recommend rejection.
Quote: Oliver Wendell Holmes, Sr. described bigotry in the following quotation: “The mind of a bigot is like the pupil of the eye; the more light you pour upon it, the more it will contract.” (Wikipedia) A further complaint of lack of objectivity by DAE Beamish resulted in an appeal to a second PRL Divisional Associate Editor (appointed by PRL Senior Editor)
The DAE (N. Brilliantov) wrote: “I have carefully studied all the materials related to your submission: your manuscript, the comments of the referees and your response to the comments. I have also studied the letter by PRL DAE Dr. Beamish as well as your response to his letter and some additional materials related to your submission, e.g. your papers and papers of other researches on the topic. I have found that the consideration of the referees and the PRL DAE Beamish was fair and unbiased, and I agree with many of their comments, although some of your responses to the criticism are convincing. Unfortunately, I have to confirm the previous decision of the editor, that the paper is not appropriate for the Physical Review Letter.”
This first paragraph addresses the PRL administration; he has served his debt as DAE by upholding their decision, by supporting the bigotry and prejudice of three anonymous referees. Notice that nowhere (below) does he say which of their comments he does not agree with.
DAE: “After exploring all the materials I come to the conclusion that you did not manage to expose with the clarity and convincingness, required for the Physical Review Letters, the main claim of your study. Please note that the acceptance of an article to the Phys. Rev. Letters requires not only novelty and sound scientific content of the submission but also a possibility of a non-expert in the field to understand the arguments without addressing to special literature. Let me ensure you that I analyzed in deep your conjecture, and read the according literature. Moreover, let me also mention that I have a few articles on the topic of liquid criticality, including the MC studies of the phase diagram of a square-well fluid (see my publication list on my webpage, http://www.math.le.ac.uk/people/nb144. Therefore, below I present my view on the discussed problem which could be helpful for you if you would like to find more supporting arguments for your hypothesis.”
This paragraph is essentially political, and based upon personal prejudice as evidenced by the self-citation. The references referred to on that website are irrelevant to this debate. Also, again, this report, so far, fails to address the specific scientific points on which basis this PRL paper has been rejected.
DAE: “In your paper you suggest a new view on the phase diagram of liquid, which is supposed to be a paradigmatic change of the present understanding of the critical point. I believe that this is a very serious claim, which must be supported with much more detailed, diverse and convincing arguments. I doubt that this may be, in principle done, in a short letter, corresponding to the Physical Review Letters format.”
Why “supposed to be”? This is yet more bigotry; the detailed arguments are contained references [3,4] of this PRL which Brilliantov claims to have read!
DAE: “For example, your claim that there is two lines of percolation transitions; these are well defined for hard-core and square-well liquids that you discuss in your papers (e.g. in Ref. ). Then you make a statement that similar transitions are expected in real liquids, like argon. It could be qualitatively true, but if one wants to make the according quantitative definitions for liquids with a realistic potential, like argon, one needs to admit large uncertainties for both transitions. Indeed, there is an uncertainty in choosing the hard core diameter for the realistic potential for the first percolation transition, as well as the uncertainty in definition of the criterion when two molecules are connected for the second transition (obviously, this may be unambiguously done for a square-well liquid). Hence an unambiguous microscopic definition of these transitions for real fluids is lacking.”
Brilliantov is meant to act as a judge in deciding disputed scientific points, which he ignores completely. Instead, he looks for alternative reasons for rejection, that are not already rebutted, as though he were a 4th referee, knowing that referees A, B and C have failed to produce cogent counter scientific reasons for rejection. Regarding the scientific point, all the new observations are in fact phenomenological, so the definition of a system spanning cluster at this stage does not require a molecular-level definition based upon an arbitrary distance parameter for the science to hold good. A simple rule of classical Gibbsian thermodynamics that Brilliantov doesn’t seem to understand is “don’t confuse statistical mechanics with classical thermodynamics”.
DAE: “Therefore, in your article you suggest to use a macroscopic approach: Namely, you suggest to interpret the discontinuities in the slope of the pressure versus density isotherms for seven experimental supercritical isotherms of argon from the experimental data of Gilgen et al., Refs. [6,7]. In your article, however you do not give the respective analysis for these isotherms, that is, from the raw data given in the Figure 2 of your paper these discontinuities are not visible. You need to present detailed explanations which prove that there indeed exist the slope discontinuities. However, I believe that this would be a hard task to convincingly prove the existence of the claimed discontinuities from the set of the discrete experimental point: As far as I understand the problem, one would need to obtain experimental data near the points of the expected slope discontinuities with extremely small density step, that is, to perform precise measurements in the vicinity of this points. Alternatively, one can try to make the according large-scale MD simulations, but it may well be, that the discontinuities appear only in the thermodynamic limit, which is hardly accessible for modern computers. Anyhow, your present claim of the discontinuities and percolation lines for real fluids is far from being convincing.”
Brilliantov, being completely unable to find fault with my counter science arguments and rebuttals of referees A, B, and C, here looks for new objections in a desperate attempt to justify rejecting the paper by further adding his own prejudices?
DAE: “Another problem with your conjecture about a line of critical states refers to numerous experimental data for the behavior of the order parameter (difference of the liquid and gas densities for the case of interest) near the critical point. It is well known and reported in many experiments that the order parameter may be expressed with a high accuracy by the relation, ρl − ρg = A |T − Tc|γ gamma is one of the critical indexes. Note that this is a purely experimental finding, the way how the experimental data may be fitted by a mathematical expression. What I want to stress, is that the experimental data indicate the existence of some special temperature (T − Tc) which allows to describe the experiment. It is also important to note that all studied liquids obey the above law, with approximately the same critical exponents (see e.g. Shang-ken Ma “Modern Theory of Critical Phenomena”). How does this bunch of experimental data concur with your conjecture of a line of critical states?”
This is another new argument, not considered by referees A, B and C. Of course, the theory referred to by Brilliantov is wholly inconsistent with the line of critical states. My view is that the successful parameterization of experimental data of state functions to something resembling a cubic of 1/(T − Tc) could be fortuitous and tells us nothing about the science of liquid-gas criticality.
DAE: “At least you must admit that there is a special point on your line, right? That is, you must admit that there are plenty of experimental works which indicate the existence of a special temperature, which conventionally called critical temperature”.
Again, another nonsensical query: of course there is a critical temperature, above which a gas cannot be liquefied by the application of higher pressure, but there is no “special point” on the Gibbs density ρ(p,T) surface. There are two thermodynamic state points corresponding to the maximum vapor density, and the minimum coexisting liquid density, at the intersection of the percolation loci PA and PB in the p-T planar projection.
DAE: “There is also a lot of other reasons, why it is difficult to accept your hypothesis. Among these are similarity of magnetic and liquid criticality (see e.g. the above book of Shang-ken Ma), which would be very difficult to explain within your view on liquid criticality, while it is easy to explain and even formally (mathematically) prove within the conventional view on the liquid criticality. One can also mention the RG analysis of critical behavior, which also indicates the existence of an isolated stable point in the RG fluxes (that is, a single critical point), but not a line of stable states (that is a line of critical state). Strictly speaking, the RG analysis has been performed for magnetics, but it may be proven that the liquid Hamiltonian may be mapped onto the Hamiltonian of magnetics, which implies the same topology of the RG fluxes for the Hamiltonian of liquids.”
Nothing is “proven” about liquid-gas criticality within the universality conjecture; this statement is totally incorrect, and indeed irrelevant to the new science we seek to report. This DAE is prejudiced in his defense of universality between non-Gibbsian statistical mechanics models which are lattice-gas like systems with no pV work, and hence no Gibbs chemical potential, such as the magnetic lattices to which he refers. Gibbs thermodynamic equilibrium systems, that convert heat and work reversibly, do not belong to that “universality” class to which he refers. One could argue that these lattice gases are not strictly (classical) thermodynamic systems.
DAE: “To conclude, I believe that there is too many experimental and theoretical results that support the present view on the critical phenomena, while the suggested hypothesis is not able to explain these.”
Quite the opposite: in 140 years of experimentation, and latterly simulation, no one has measured, or simulated, directly a liquid-gas critical volume. This DAE doesn’t seem to understand, the only “hypothesis” in this debate is that proposed by van der Waals. This paper explains why his “critical point” theory has never been substantiated. There is no new hypothesis here; rather, there is an alternative self-consistent re-interpretation of all the existing thermodynamic phenomenology.
[A1] REFERENCES
- [A2] Woodcock, L.V. (2012) Fluid phases of argon, LANL, arXiv. cond-mat. stat-mech. 1206.2638.
- [A3] Throwe, J. (2012) Private Communications Referee Reports. Physical Review Letters.
- [A4] Beamish, J. (31 July 2012) Private Communication. Physical Review Letters, University of Alberta, Edmonton.
- [A5] Brilliantov, N.D. (22 October 2012) Private Communication. Physical Review Letters, University of Leicester, Leicester.

