Natural Science
Vol.4 No.4(2012), Article ID:18625,8 pages DOI:10.4236/ns.2012.44033
Occurrence of Fibonacci numbers in development and structure of animal forms: Phylogenetic observations and epigenetic significance
![]()
Bioderm Technologies, Inc., Chesterfield, UK; jjwille@aol.com
Received 14 February 2012; revised 18 March 2012; accepted 30 March 2012
Keywords: animal body plan; Fibonacci numbers (n); Hox genes; nested triads; phylogeny; recursive transition networks; segmentation
ABSTRACT
A survey of zoological literature affirmed the wide occurrence of Fibonacci numbers in the organization of acellular and prokaryotic life forms as well as in some eukaryotic protistans and in the embryonic development and adult forms of many living and fossil remains of metazoan animals. A detailed comparative analysis of the axial skeleton of a fossil fish and humans revealed a new rule of the “nested triad” of bones organized along the proximal to distal axis of limb appendages. This growth pattern and its ubiquity among living vertebrates appear to underlie a profound rule of pattern formation that is dictated in part by the genetics and epigenetic mechanisms of stem cell clonal development.
1. INTRODUCTION
In his Liber Abachi, published in 1202, Leonardo da Pisa, better known as Fibonacci, considered the question of how many pairs of rabbits would you have after N breeding seasons, starting with a simple immature pair and assuming idealized rules for growth of their number as represented (Figure 1).
The Fibonacci series has been encountered in plant morphogenesis as the phenomenon of Phyllotaxis seen in the spiraled seeds of the sunflower, fir cones, and in animal morphology such as the spiraled shells in foraminiferan and in molluscan shells [1]. The basic biology of phyllotaxis is well documented and attempts made to provide an underlying mechanism. However, a raison d’etre and mathematical basis has been the subject of considerable interest and controversy [2,3]. Recently,

Figure 1. Idealized diagram of the rabbit Fibonacci pattern formation.
(Mario Livio in the Golden Ratio) [4] provided an analog explanation based on physical experiments [4,5], that phyllotaxis simply represents such a state of minimal energy of mutually repelling buds. Another recent mechanistic explanation of phyllotaxis [2,6], is that “the growth dynamics of cell division causes primordia to be pushed into golden-angle relationships, and as the cells grow and move, they create forces that affect neighboring cells”. In all these above examples, the conceptual theme is selfsimilarity of articulated parts of plants and animals. The Fibonacci numbers are a prime example of self-similarity. The Fibonacci numbers are simply the arithmetic consequence of multiplying each number by 1.6, and rounding to the nearest integer. Self-similarity of Fibonacci numbers has been amply discussed in relation to recursive transitional networks in computer science [7], in the mathematics of reiterative sequences exemplified in chaos [8], and an outcome of reiterative process even in the simplest of non-linear dynamical systems [9]. Here, we document the pervasive occurrence of Fibonacci numbers throughout the animal kingdom in both adult organism and in embryonic development, provide a cellular basis, and propose a novel epigenetic mechanism.
2. RESULTS
Prolife and Prokaryotes
Among acellular life forms the viral head capsid proteins are often arranged as 12-five-sided faces (icosahedrons) e.g., Phi-X 174, a single-stranded DNA bacteriophage and Human Adenovirus and hepatitis virus); the spherical Rotovirus has a sunflower-like disc arrangement of protein subunits, reminiscent of Fibonacci number of spiraled parastiches in plants [10].
Among prokaryotes, motile single-celled bacteria often arrange themselves into dynamic growth patterns resembling Fibonacci patterns either as alternating concentric rings of dense and less dense cells [11] or into spirals [12]. The authors have ascribed the results to an iterative process in which the number of rings and or spirals is the result feedback between genetic circuits that generate inhibitory signals, i.e. morphogens, combined with growth stimulatory growth circuits and modeled as non-linear dynamics.
3. EUCARYOTIC PROTOZOA
Among the eucaryotes, the single-celled foraminferan amoeba, Nummelites laevigatus, builds a calcareous exoskeleton with the Fibonacci number of thirteen (13) spiral chambers. The silicaceous skeletons of the amoeboid protozoan Radiolaria display an almost infinite variety of pentagonal or Fibonacci number five (5) observed for five-sided forms much documented by Ernest Haeckel’s Challenger Expedition, and reproduced elsewhere [3]. The ciliated protozoa with their highly differentiated surface architecture provide many examples of reiterated subcellular components as revealed by silver line staining methods [13]. Most ciliate species have a characteristic stable number or range of numbers of ciliary rows arranged circumferentially and oriented along the anterio-posterior axis known as kineties. The modal number of kineties differs in different ciliate species, known as their corticotype. For Tetrahymena thermophila, the best studied species, the corticotype exhibits a range of 19 - 21 kineties with a stable modal Fibonacci number of twenty-one (21), when the truncated paroral kinety is included in the count [14]. Under natural condition of starvation, cells with a corticotype of 18 - 19 kineties undergo oral replacement and insertion of two additional postoral kineties, resulting in the stable modal Fibonacci number of twenty-one (21) kineties, while cells with the stable Fibonacci number of 21 kineties are unaffected by these conditions [15]. Further analysis of maternal inheritance of corticotype transmission revealed that there a sharp break in the variance that occurs 30 - 50 clonal fissions at exactly the Fibonacci number of twenty-one (21) [16]. Rearrangements of corticotype number also occur in the exconjugant pairs after sexual reproduction in Tetrahymena pyriformis [17]. In a cross between a 10 different parents arising from a maternal line having a stable corticotype with a Fibonacci number of twenty-one (21) crossed with 10 different parents arising from a maternal line with un unstable corticotype of 27 - 28 following separation of the exconjugant pair all clones derived from the maternal line with 21 kineties continued with a stable modal number of 21 kineties, while the maternal exconjugant line with an originally high and unstable model number of kineties drifted downward toward the stable modal number of 21 [17]. Similarly for the much larger ciliate Paramecium tetraaurelia, the corticotype number for the uninterrupted right field the modal number of kineties is the Fibonacci number thirty-four (34) [18]. There are many other examples of Fibonacci number of subcellular cortical components in other ciliate species. The ciliate Loxodes striatus displays the Fibonacci number of thirteen (13) total cortical surface kineties and a Fibonacci number of 3 - 5 anterior left buccal kineties [19]. The trichostominid ciliate Tillina magna undergoes periodic encystment in which all traces of ciliature disappear (Figure 2). Upon excystment, the immature form displays a Fibonacci number of twenty-one (21) kineties and upon maturation and torsion the adult form displays additional kineties of the Fibonacci number of thirty-four (34) kineties [20].
The Oligotrich ciliate, Stylonychia mytilus is distinguished by cirri located on their ventral surface (Figure 3).
The frontal cirri are arranged in groups of 3 and 5; the abdominal cirri are arranged in group of 3, and the posterior cirri in groups 3 and 5 all Fibonacci numbers. These
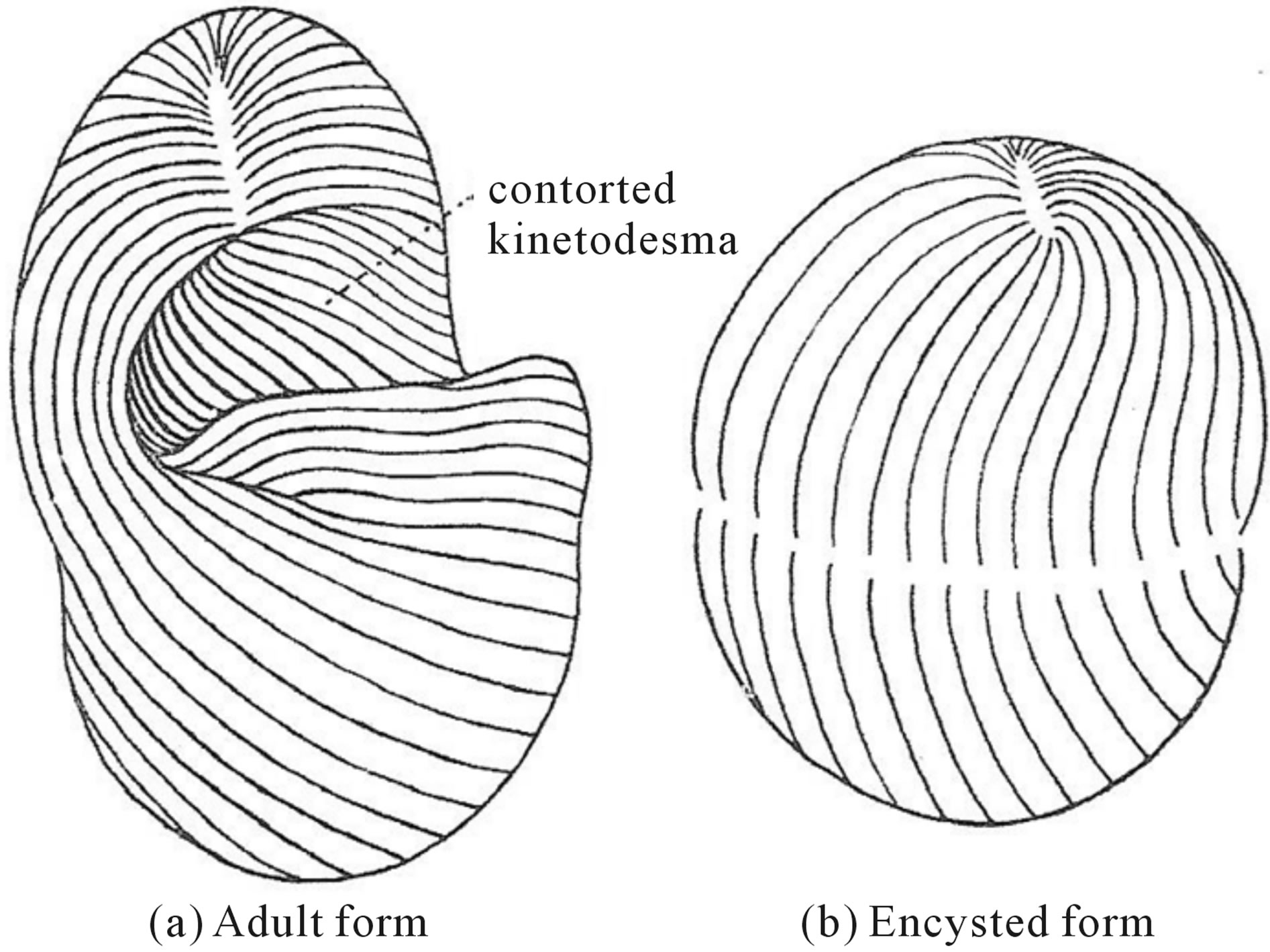
Figure 2. Torsion of the kineties after excystment of Tillina magna (after Corliss cited in BEPS [20].
grouping arise at fixed cortical sites along particular ventral meridian of kineties [20]. A theoretical basis for the reproduction of kineties during cell division and their stable propagation was proposed earlier, based on detailed electron microscopic studies of ciliary body formation. A paratene is defined as linear catenaries of new ciliary corpuscles that develop semi-conservatively, one unit at a time, just posterior to an old trichocyst and just anterior to an old ciliary corpuscle as envisioned along a kinety as a abstract cortical construct (Figure 4) [21].
This reproductive mechanism assures continuity of corticotype in Paramecium by substituting modal Fibonacci number of eighty-nine (89) with a range of 70 to 100 cortical loci accomplished without any additional ad

Figure 3. Cirri of Stylonychia mytilus (ventral view) (after BEPS [20]).

Figure 4. Mapping of kineties and paratenes (after Ehret, 1967 [21]).
hoc postulates.
4. EARLY METAZOANS
Metazoan life forms are multicellular organisms composed of tissue layers. The simplest two-layered or diploblastic tissue grade, intermediate forms between protozoan and the three-layered or triploblastic, metazoans are the common sponges of the Phylum Porifera They produce calcareous or silcaceous spicules that lie within a radially symmetrical body plan from scattered cells within the gelatinous middle layer of a hollow tube-like body (Figure 5).
Fibonacci numbered three (3) tri-rayed spicule formation of three spicule-forming cells to form a three-rayed compound spicule. The spicule projections are then oriented with two pointing anteriorly and the third posteriorly. Together the tri-rayed spicules form a branching reiterated network as body cover [20]. The Phylum Coelenterata shares the same diploblastic tissue grade as sponges, except that coursing through the middle layer or mesoglea, are well-formed nerve cells that coordinate body movements. All three aquatic classes of Coelenterates are radially symmetrical and are characterized by socalled “alteration of generations,” The sessile polyp stage alternates with a motile or migratory medusa stage, the latter connecting the two stages by a fertilized embryo with a free-swimming larval form that settles down to form a polyp. The class Hydroidea is exemplified by
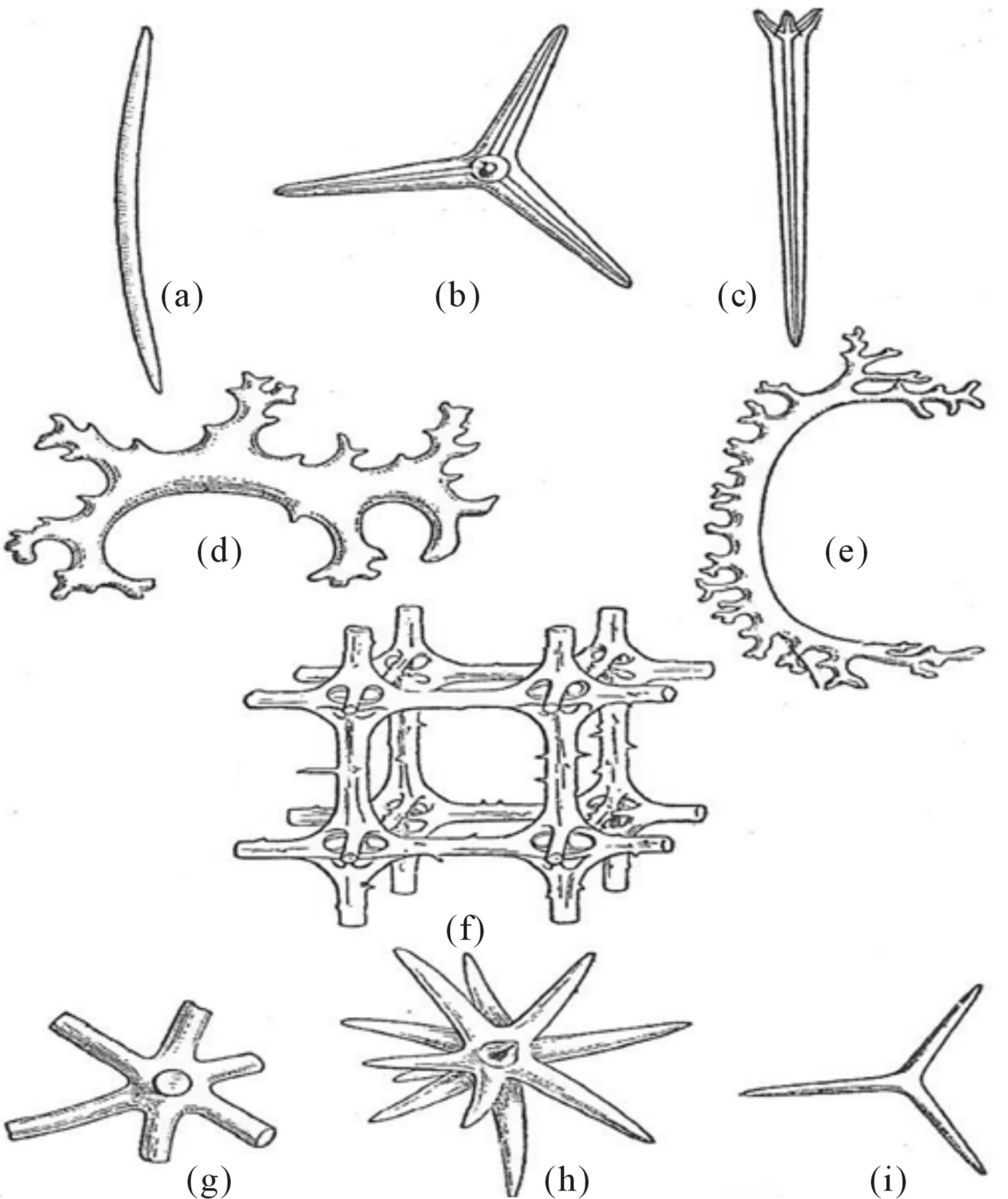
Figure 5. Calcareous sponge spicules (note (b) and (f)). After BEPS [20].
Hydra, a single sessile tube-like polyp, and the sessile colonial hydroid, Obelia (Figure 6).
It reproduces asexually by a budding process along the trunk of the body but it can also form a gonadal bud that develops into the free-swimming medusa stage. The head of the polyp opens at the mouth of the hollow tube and is surrounded by a ring of a Fibonacci number of thirteen (13) solid tentacles [22]. Medusa forms in all classes of coelenterates when viewed in the horizontal plane have an upper aboral side and an under oral side, which universally display a Fibonacci number in their eight-fold (8) radial symmetry (figure 7).
Among sessile colonial Actinozoan coelenterates the order, Octoradiata, commonly known as “Dead men’s fingers” are characterized by the Fibonacchi number of eight (8) mesenteries and eight (8) tentacles. Finally, the subphylum Ctentophores, a common pelagic form that has a bilateral symmetry secondarily imposed on radial symmetry. The Ctenophore, Pleuribrachia bachei, has an ovoid shaped body with a Fibonacci number of eight (8) meridional rows of comb plates of cilia (Figure 8) [22].
Surveying the truly tribloblastic acoelomate phylum, Platyhelmenthes, the triclad Turbullarian flatworm, Dendrocoelum lacteum, has no true body cavity but the gut has the Fibonacci number of three (3) branches. The body is bilaterally symmetrical with an anterior head end with dorsal eyes and nerve ganglia, and a tail end from which an elongated oral proboscis extends. The paired (Fibonacci number (2) lateral reproductive organs are present with both a male and female paired canals in this hermaphroditic organism. The paired lateral longitudinal excretory canals also display the Fibonacci number of
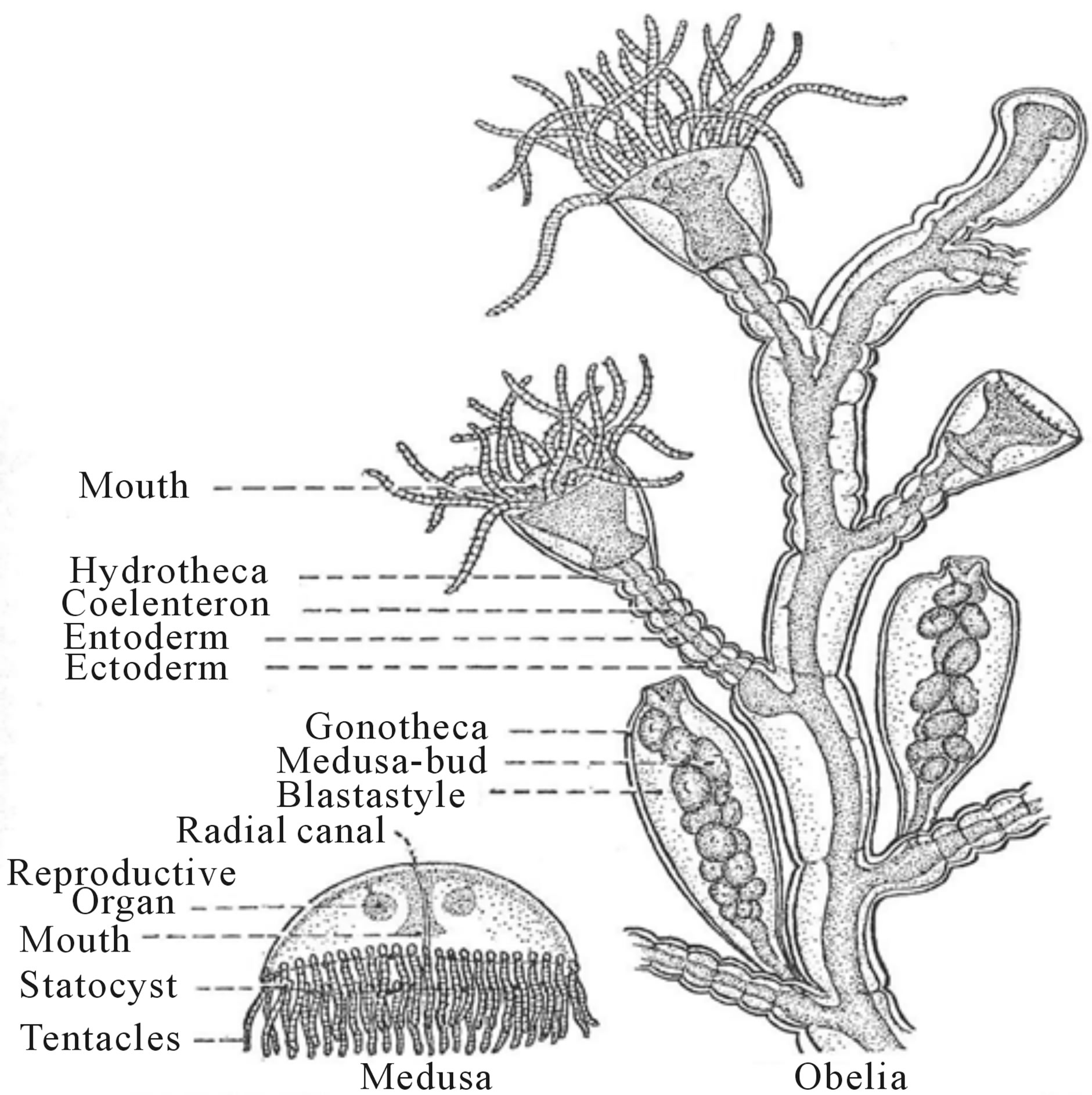
Figure 6. Obelia hydrozoan colonial coelenterate (after Potter, Textbook of Zoology, 2nd Ed. [22]).
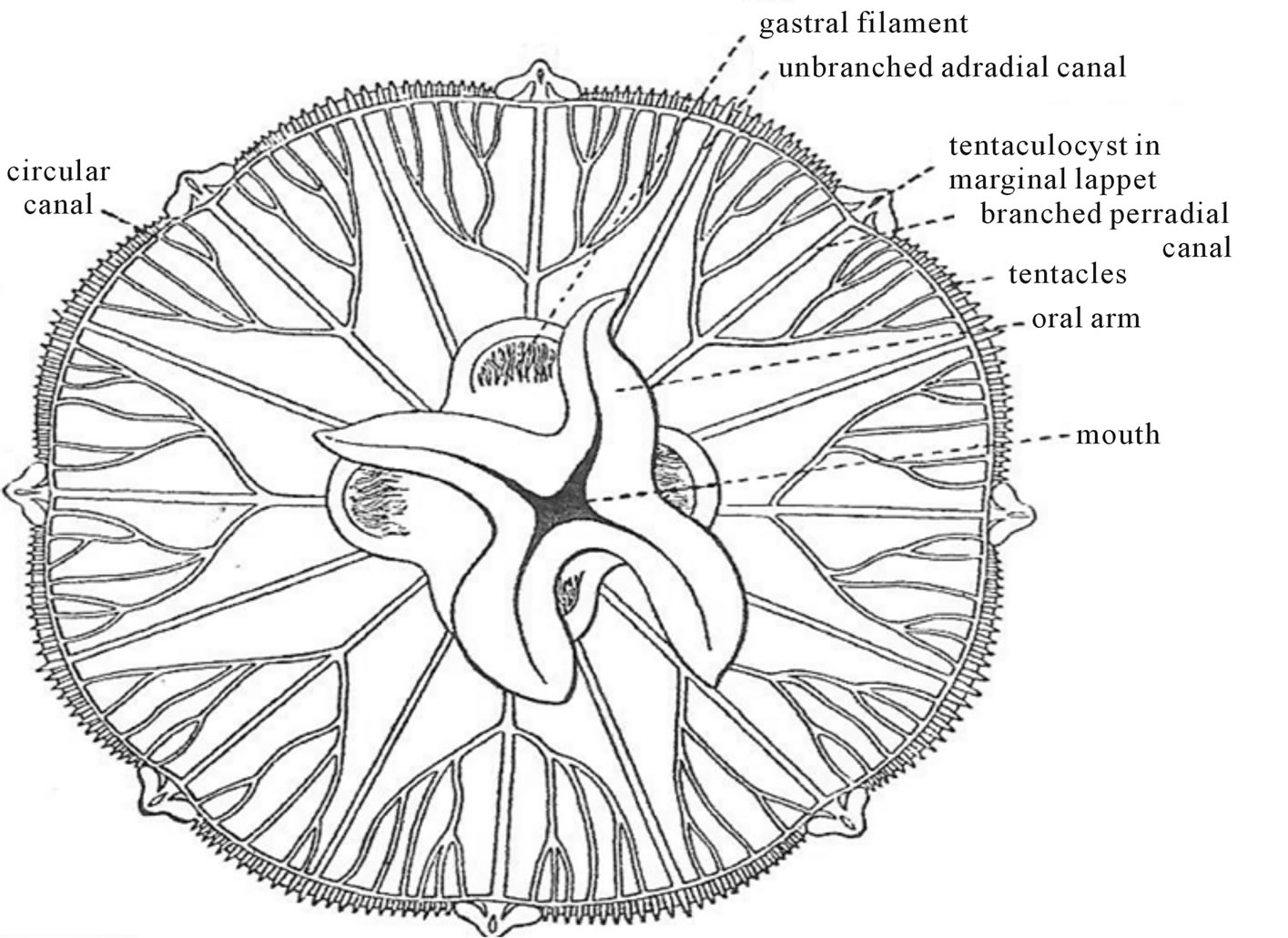
Figure 7. Aurelia aurita, a Discomedusae form (after BEPS [20]).
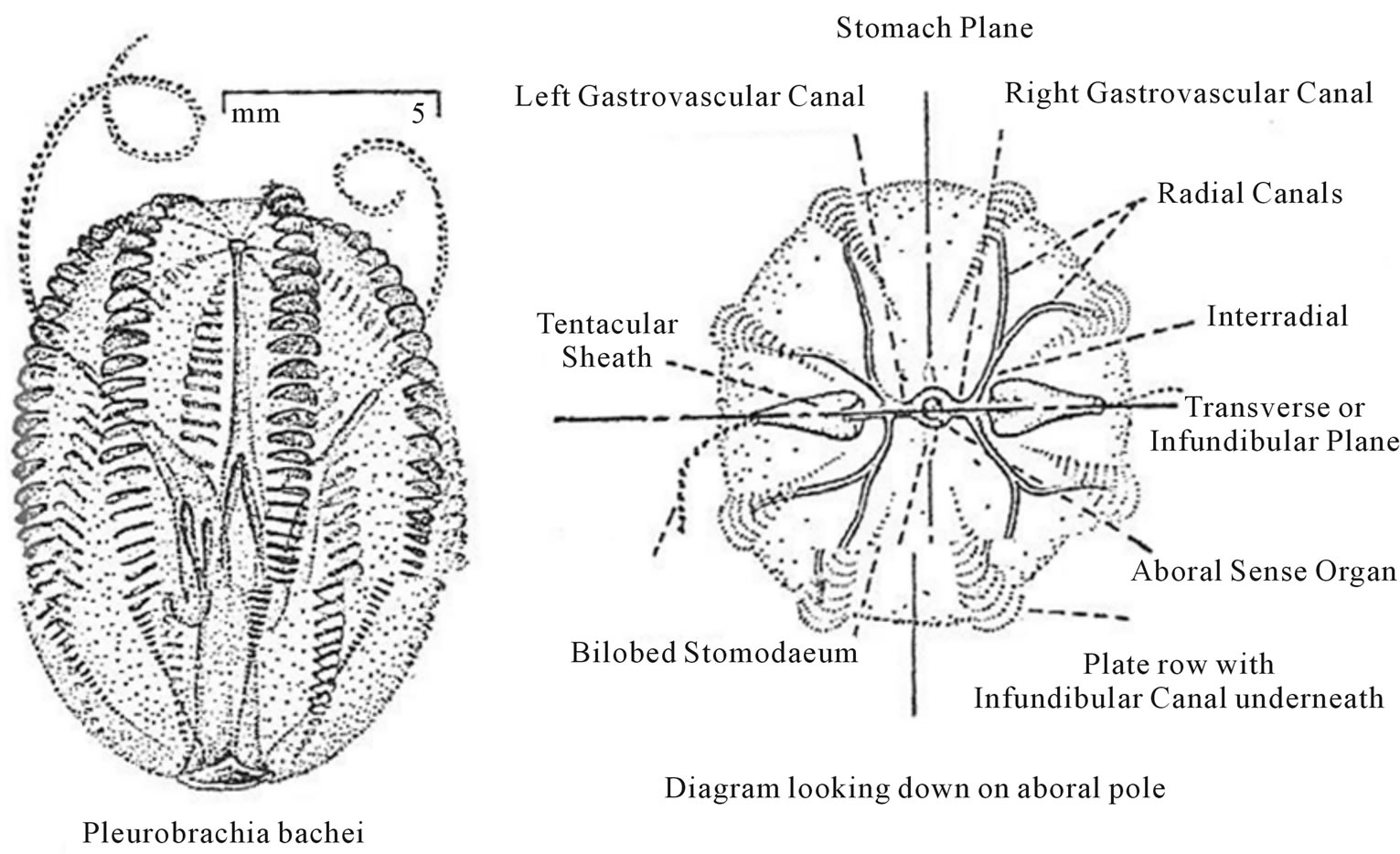
Figure 8. Pacific comb jelly (after Potter [22]).
eight (8) non-segmentally spaced excretory pores. Turbullarian flatworms can reproduce asexually with a Fibonacci number of three (3) individuals forming a chain budded from the hind end body of one individual. An extraordinary example of Fibonacci numbers is seen in the Nemertinean acoelomate round worm Caenorhabditis elgans perhaps, the most recently studied metazoan invertebrate. This is due to the fact that its complete development can be traced and clonally mapped to its fixed total number of 959 somatic cells of the adult hermaphrodite. Consider that there should be 1024 or 210 somatic cells, if all were derived by 10 undifferentiated binary cell divisions. Also, it is estimated that there are an additional 32 or 25 germ line cells [23]. Thus, the adult hermaphrodite has a grand total of 891 cells, which is close to the 15th place Fibonacci sequence number of 897. Statistical analysis comparing the Fibonacci versus binary geometric sequence by null hypothesis suggests that the 15 iterations of the Fibonacci sequence is a better fit than the binary geometric progression at approximating the clonal pathway to the adult total cell number. This may be related to the known loss of 131 cells during development by commitment to programmed cell death.
5. PHYLUM ANNELIDA
The architecture of an Annelid worm represents one of the overarching principles of body plans in zoology, metamerism, or the repeated segmentation of body into numerous nearly identical units. For the sake of clarity and simplicity we will restrict the study of the occurrence of Fibonacci numbers to the well-know representative of the Oligochaete class, the earthworm, Lumbricus terrestris shown in Figure 9, based on previous descriptions [22].
Segments by convention are listed as Roman numerals. The total number of segments is indeterminate beyond the clitellum (segment XXXIV), a Fibonacci number of thirty-four (34). External as well as internals structures are definitely related to specific segments. The first segment (I) is incomplete due to the opening of the mouth on the ventral side. A Fibonacci number of five (5) paired hearts is located at segments VII through XI). Segment XIII, a Fibonacci number thirteen (13), marks the

Figure 9. Segemental anatomy of the earthworm, Lumbricus terrestris (after Potter [22]).
boundary between the opening (pores) of paired oviducts on each side of segment XIV. Segment VIII, a Fibonacci number of eight (8), marks the boundary for the paired opening (pores) of the seminal receptacles in groves between segments IX through XI, and within the body lie a Fibonacci number of three (3) pairs of seminal vesicles between the boundaries of segments VIII and XIII. Ovaries are located within on each side of segment XIII, the Fibonacci number of thirteen (13). Openings of the vas deferentia, which convey sperm to the outside, are located on each side of the anterior part of segment XV. The anterior boundary of the seminal groove runs from segments XX-XXI through XXV. In sexually mature worms segments XXX, XXXI, XXXII through segments XXXVII are swollen to form the clitellum, which function to secrete a cocoon in which eggs are deposited. Every segment, except the first and last, bears a total of four stiff bristles or chitinous setae. Segment III, a Fibonacci number of three (3), marks the boundary for the start of paired nephridiopores, the openings of the paired nephridia, or excretory organs, which are present on all posteriorly located segments. The digestive system is demarcated by the mouth which runs through segments I and III (Fibonacci numbers); the pharynx starts at segment II and runs through segment V. The esophagus runs straight through from segment VI to segment XIV. The boundaries of the Fibonacci number of three (3) pairs of lateral pouches of the calciferous glands lies within segments X through segment XII. The crop runs from end of segment XIV through XVI followed by a muscular gizzard from segments XVII through XVIII. The thinwalled intestine extends from the gizzard to the anus that opens through the last segment. It should be noted that the entire digestive tube courses through the hollow body cavity independent of the septae separating each segment and, thus independent of metamerism. The nervous system of the earthworm consists of a brain composed of fours ganglia, that lie at the boundary of segment I and ends at the boundary of segment III. A ventral nerve cord extends posteriorly the length of the body with one ganglion and the Fibonacci number of three (3) pairs of nerves branching out from the cord in each segment. Earthworms have the favorite subject of many studies on regeneration. A cut made ahead of segment XVIII will result in the regeneration of new segments I through V), which are Fibonacci number boundries) at the anterior end, but no new anterior end segments regenerate if cuts made posterior to segment XVIII. However, any cuts made at posterior end to this tail segment will regenerate a new tail end. In summary, we have identified Fibonacci numbered segments, which are either the boundary or site(s) at which key developmental event occur for the formation of tissues and organs in the anterio-posterior axis of the body plan of annelids. The further significance of the role of segment XVIII for the regeneration of the first five segments of a new anterior end remains enigmatic from the Fibonacci number point of view. To be sure, there are many other examples in the other two annelid classes. In the typical Hirudinean leeches the constitution of the body is remarkably constant Fibonacci number of thirty-four (34) segments [20].
6. PHYLUM ARTHROPODA
“…the way was clear for careful observer to map the barnacle anatomy against the twenty-one segments of Milne-Edward’s archetypal crustacean” Darwin and the Barnacle, Rebecca Scott, p. 208, 2003 [24].
The phylum Arthropoda (jointed legs) is a group of invertebrate animals that have a bilateral segmented body plan, that again exemplify the principle of metamerism. There are eight different classes all of which display a body segmented into an evolutionary conserved Fibonacci number of twenty-one (21) [20] somites, which is more often apparent in larval stages than the adult. Trilobites are fossil ancestral arthropods whose body is divided into a Fibonacci number of three (3) lobes or tagma. In the fossil species, Teratopsis, the body parts arises from a primitive Fibonacci number of thirteen (13) somites. For the four living arthropoda (Onychophora, Crustacea, Insecta, and Myripoda), the body is again subdivided in to the Fibonacci number of three (3) tagma (head, trunk and abdomen). The allotment of somites to these tagma differ in each of these classes, but all arthropoda have the Fibonaccci number of two (2) appendages per segment. The nervous system consist of the Fibonacci number of two (2) longitudinal ventral cords, a dorsal brain recruited from glanglia of the Fibonacci number of the first three (3) somites. There is a pair of ganglia for each body somites. We see, therefore, a system built on the principle of bifurcation of tagma parts with paired appendages per somite including paired epipodites that extend from the bases of the legs that serve as respiratory or gill-like structures. The Onychophoran, genus Scolopendra, has a centipede body plan with a Fibonacci number of twenty-one (21) metameric segments (Figure 10) [22].
A survey of the number of somites in the three body divisions (tagma: head, thorax and abdomen) among the eight orders of crustaceans has been categorized [20]. Of interest is the higher Fibonacci number of thirty-four (34) somites found in the Onychophorea, thought to be related to the most primitive ancestor of the crustacean. Note also that evolutionary adaption to specialized habits has led to a major reduction in abdominal somites in both the Ostracoda (7) and Cirripedia (11), and to a less extent in the Cladocera (16), Leptostraca (20), Amphipoda (19) and Decapoda (19). By contrast, the head tagma of all

Figure 10. The twenty-one body segments of the Onychophoran, Scolopendra. After Potter [22].
crustacea arises from the Fibonacci number of five (5) somites, and the thorax arises from the Fibonacci number of thirteen (13) somites in Notistraca. The Fibonacci of number of eight (8) somites are found in four other classes: Cladocera, Leptostraca, Amphipoda and Decapoda. The other three classes have a reduced number of thoracic somites: Ostracoda (2), Copepoda (7), and the Cirripedia (6). Note that these three classes also display reduced numbers of abdominal somites. A crustacean formula for the somite distribution in head (H), thorax (T), abdomen (A), and tail/telson (Te) regions is given here: H(5)/Th(13/8)/A(21)/Te(1).
The above formula is based on hypothesis that Fibonacci numbers form the basis for positioning of metameric somites of the crustacean body plan. The ideal Arthropoda subclass, Malacostrada, have only 20 somites, excluding the telson. Their formula is H(6)/T(8)/A(6). The order Leptostraca has the classical crustacean and Fibonacci number of twenty-one (21) somites. The additional somite is from the abdomen. The embryonic form of the order Mysidacea also has the additional abdominal somite. The suborder Decapoda as the name implies has the Fibonacci number of five (5) thoracic pairs of legs as does the suborder Penaeidea to which belong the prawn, shrimp, crayfish and lobsters. The class Insecta (Hexapoda) is distinguished by all orders having the Fibonacci number of three (3) pairs of legs among all orders. The head consists of 6 segments with the Fibonacci number of five (5) somites with paired appendages, the thorax the Fibonacci number of three (3) segments and the abdomen has 11 segments. There are 32 orders subdivided in to two subclasses the wingless and winged orders, of which he latter are anatomically organized in to four sections. In all orders the legs are made up of the Fibonacci number of five (5) main segments; the last segment of which is bifurcated into claws. Peculiarly, the pattern of wing venation is varied among insects but cluster about the Fibonacci number of twenty-one (21) delineated areas. Dipteran and Hymenopteran larvae have the Fibonacci number of thirteen (13) segments including both head and abdomen with a formula: T(5)/A(8) [20] (see figure 11).
In the class Arachnida, the anterior part of the body is never divided in to a head and thorax and contains 6 adult segments—a single preoral and the Fibonacci number of five (5) postoral segments; the posterior part consists of the Fibonacci number of thirteen (13) segments. There are twelve orders. Larval scorpions have a body plan formula: T(5)/A(7), while the adult has a formula: T(8)/A(5), excluding the telson. The ancestral extinct Eurypterids, Slimonia has a total of Fibonacci number of thirteen (13) segments of the combined head and throrax with an additional Fibonacci number of five (5) abdominal segments. Fibonacci numbers are also seen in Limulus polyphemus, the only surviving member of the order Xiphosura. It has the Fibonacci number of five (5) thoracic pairs of legs and Fibonacci number of eight (8) abdominal segments (Figure 12) [20].
The body plan of the six orders of spiders shows mainly an unsegmented abdomen. Although in embryos there are often have the Fibonacci number of five (5) pairs of rudimentary abdominal legs.
7. PHYLUM MOLLUSCA
“Inequality start curves, and when growth is diverted from the direct path it almost necessarily leads to the production of that most beautiful of curves-the spiral. Alfred R. Wallace [1].
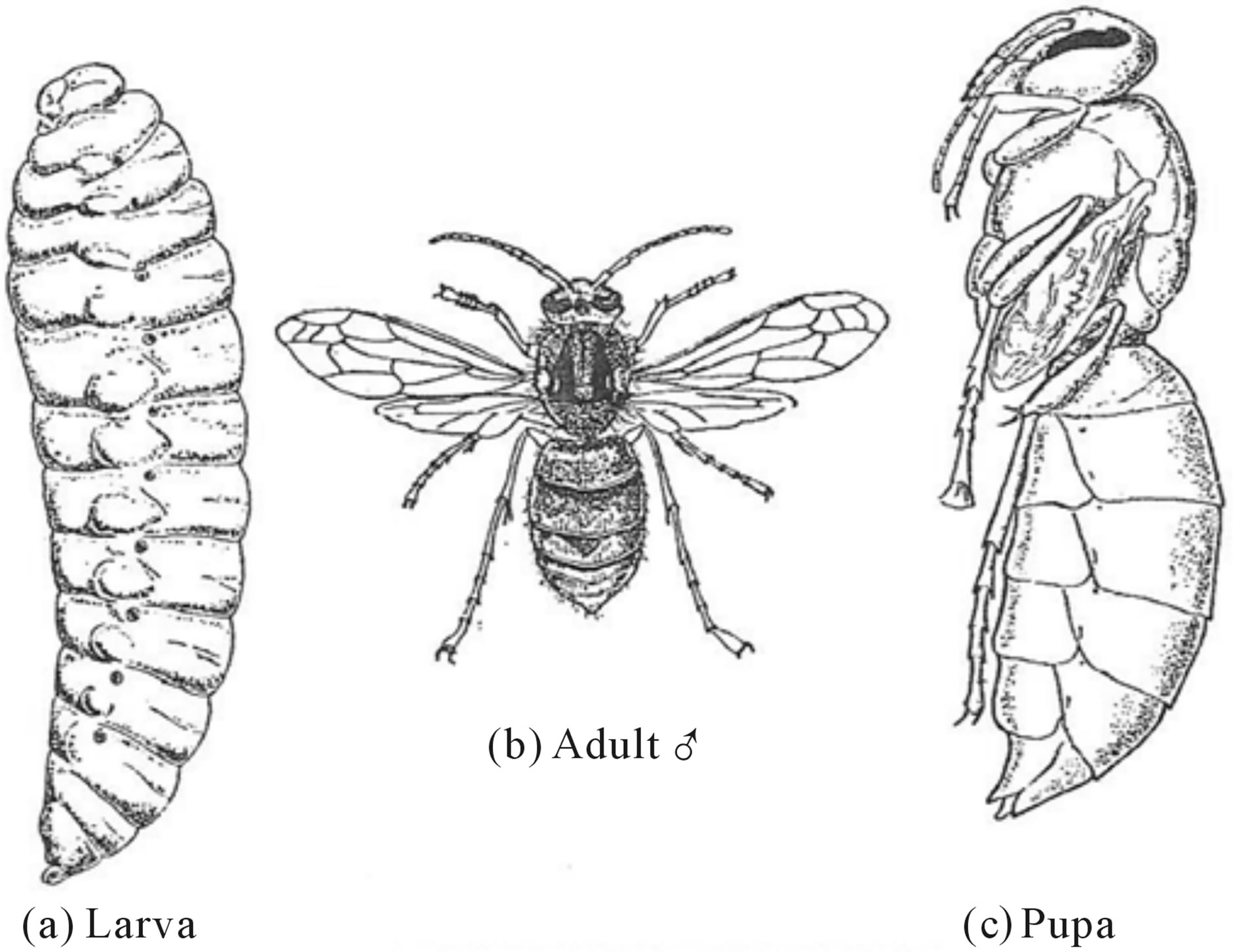
Figure 11. The thirteen body segments of the Hornet larva, Vespa crabro. After BEPS [20].
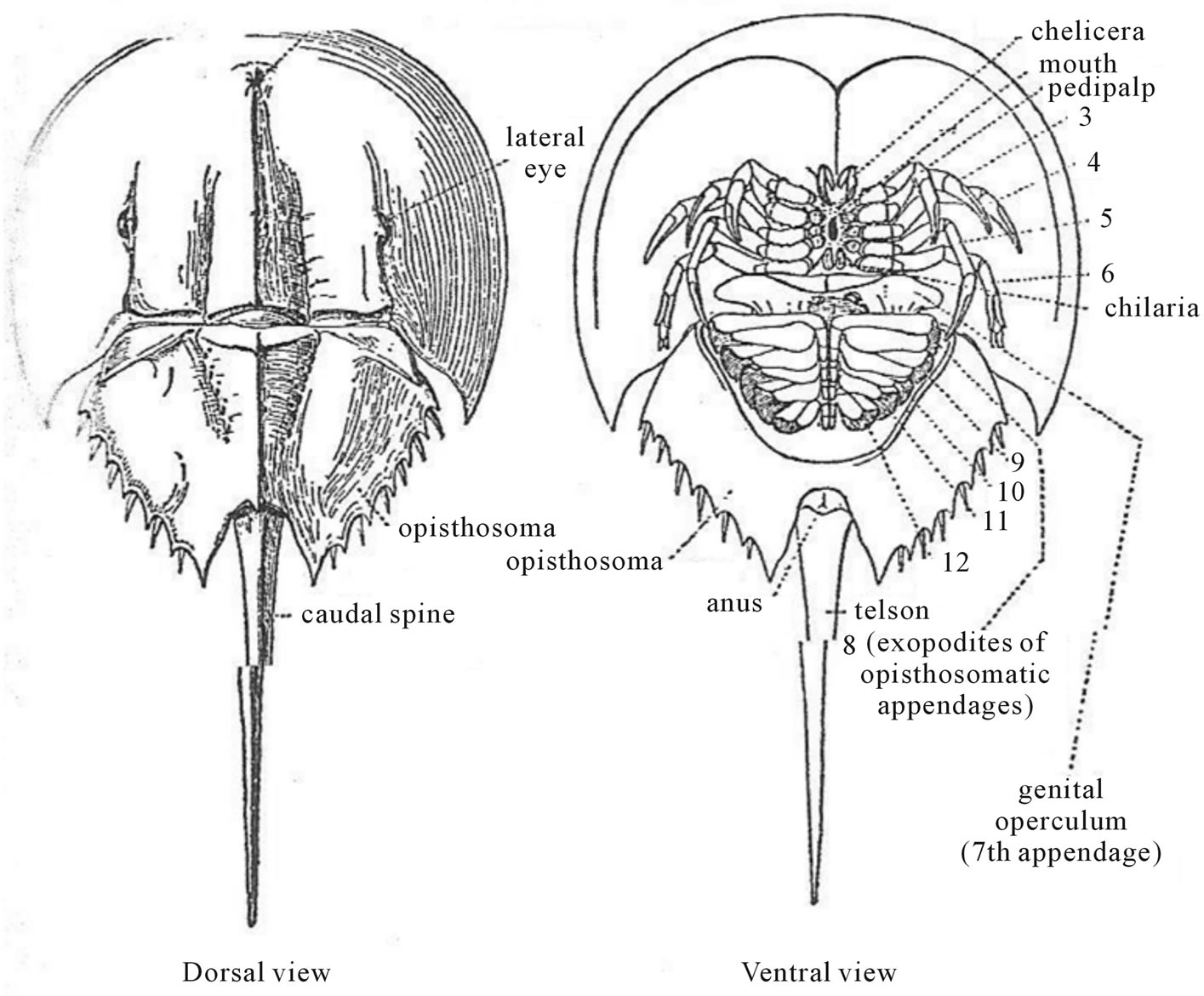
Figure 12. The body segments (ventral view) of the Horseshow Crab, Limulus polyphemus. After BEPS [20].
The phylum includes familiar animals such as snails, clams, oysters and cuttlefish. They are considered to be unsegmented. Shells are one of the most beautiful elaborations of the mollusks. Over twenty sea scallop shells of Pecten of the order, Lamellibrach were collected at random from different eastern United States locations. All had a Fibonacci number of twenty-one (21) radial ribs along the dorsal shell surface [25]. The spiraled shell of the snail, Lymnaea has Fibonacci number of five (5) turns from mouth to apex of the spiral. There are three orders of the class Amphineura, the genus Chiton has a bilateral elongated body with a calcareous dorsal mantle displaying the Fibonacci number of eight (8) transverse plates (Figure 13) [20].
The paleontological antiquity of this group is indicated by the Fibonacci number of eight (8) shell valves in fossil forms. Other living Amphineura such as deep sea species, Neopilina galatheae show a marked metamerism of the internal organs with the Fibonacci numbers of five (5) pairs of gills, five (5) pairs of dorso-ventral muscles, and three (3) more muscles near the head. There are three orders of the class Gastropoda. They are severely flattened dorso-ventrally and show no signs of body segmentation. The class Cephalopoda are represented by the familiar squid and octopus both bearing the Fibonacci number of eight (8) tentacles. Among the order Tetrabranchiata, the order Nautiloidea is represented by the chambered Nautilus; it shows signs of a primitive kind of body segmentation of the body cavity suggesting an originally metamerically segmented ancestor [20].
8. PHYLUM ECHINODERMATA
Echinoderms or “spiny skinned” animals are the familiar free-living marine animals such as starfish (Aster-
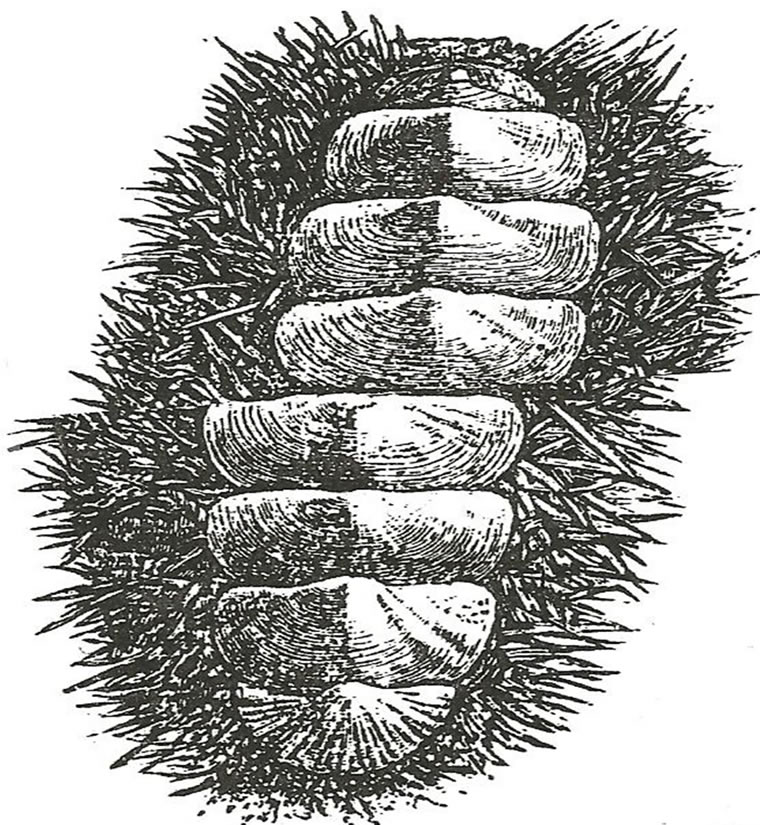
Figure 13. The eight plates of the Polyplacophran mollusk, Chiton (ventral view). After BEPS [20].
oidea), brittle stars (Ophiuroidea), sea urchins (Echinoidea), and sea cucumbers (Holothuroidea). They are generally found in the littoral zone, except for the sessile and stalked Crinoids. They are bilaterally symmetrical as larvae and radially symmetrical as adults. The body plan of Asterias, Ophiura (see Figure 14) and Echinus, three species that are representative of starfish, brittle star and sea urchins, respectively, all display the Fibonacci number of five (5) radial arms in their marked five-fold radial or pentagonal symmetry [20].
The pentagonal symmetry extends to the disposition of the various internal organs including the highly unusual water pumping or water vascular system, the digestive system and the gonadal reproductive organs. The sausage-shaped Holothurideans without the Fibonacci number of five (5) radial arms still display a five-fold radial body plan, although owing to the presence of one interradius, the body possesses a rudimentary bilateral symmetry. Crinoids do possess a Fibonacci number of five (5) pairs of long slender arms that extend from five-fold radially symmetrical body plan. Most Crinoids are extinct; those living members are stalked and live in deep water.
9. PROTOCHORDATA
The three invertebrate subphyla of Protochordata all share features of the vertebrate chordates, i.e., gill slits, dorsal hollow central nervous system, enterocoelic coelom, notochord, and postanal tail, but have no vertebral column [20]. The so-called tadpole larvae of Ascidian tunicates have segmented bodies, which resemble the chordates and their close relatives, the Cephalochordates. Both are bilaterally symmetrical with gill slits and either a partial or complete notochord, and segmental muscles. The Cephalochordate species Amphioxus, has a
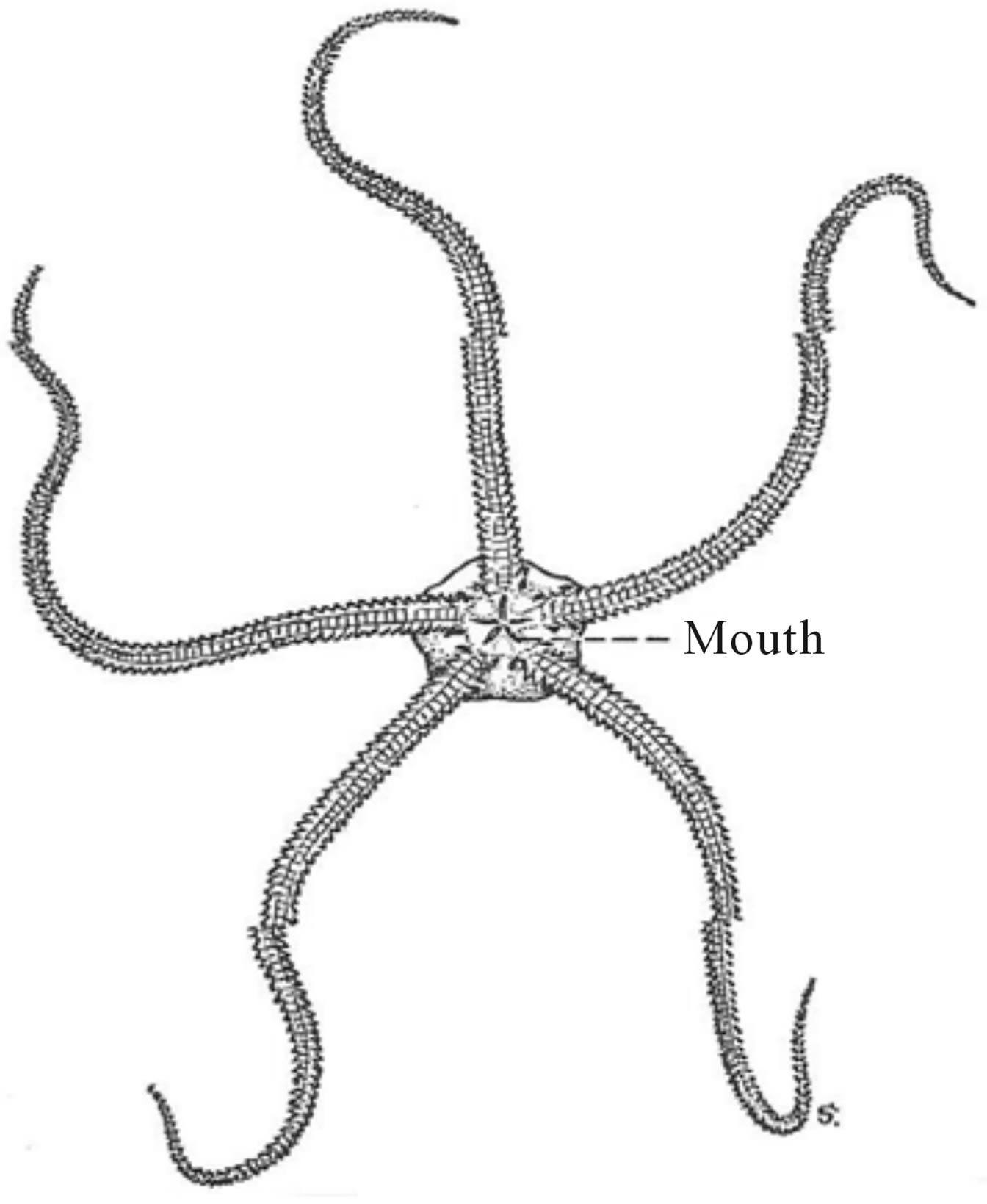
Figure 14. The five-armed Ophiuroidean, Ophiura. After Potter [22].
well formed notochord extending the full length of the fish-like body and has been conjectured to be an evolutionary forerunner of the true chordates. The number of gill slits and metameric somites of the tail hint at Fibonacci numbers, but the evidence is meager.
10. PHYLUM CHORDATA (VERTEBRATES)
These are the four classes of fish (Agnatha, Placodermi, Chondrichthyes. and Osteichthyes) and four terapods vertebrate classes (Amphibia, Reptilia, Aves, and Mammalia). All are marked by body segmentation and serial metamerism. The axial skeleton of both fossil and living representatives of each class provide abundant evidence of the “Rule of Fibonacci Numbers” defined here as markers occurring at boundaries of the developmental program of the body plan that later become specific differentiated regions of the skeleton, musculature, nervous system, heart and circulatory system. Only a cursory outline of these features will be presented here due to the overwhelming documentation available [26]. Among the specialized regions are the head, neck, gill region, trunk, tail, pectoral and pelvic girdles and associated limbs. The Fibonacci number of five (5) paired gill pouches is present in normal jawless fish (Agntha). Similarly, both the cartilage fish (Chondrichthyes) and higher bony fish (Osteichthyes) have the same Fibonacci number of five (5) pairs of gill slits. The primitive Devonian shark, Cladoselache had the archaic Fibonacci number of eight (8) gill arches including the Ist gill arch that support the moveable jaw just as do modern great white sharks. The Fibonacci number of five (5) gill slits and gill arches are also present as pharynygeal derivatives in the embryonic forms of most other vertebrate classes and found also in the human embryo. The longitudinal paired series of gill pouches is largely responsible for a segmental arrangement of the associated nerves and skeletal structures. This corresponds to the segmental arrangement of muscle myotomes, which in fish alternate with vertebral elements, and the skeletal and nervous elements associated with them [26]. Body cavities start from a primitive single hollow coelom, and in fish, amphibian split in to the Fibonacci number of two (2) cavities, the pericardium and coelom, while in the mammals it splits into the Fibonacci number of three (3) body cavities with a separate lung cavity. The circulatory system consists of primitive heart with the Fibonacci number of three (3) chambers, the ventricle, atrium and sinus venosum, and a single (1) enlarged portion of ventral aorta, the conus arteriosus. In birds and mammals the heart bends during development in to an S-shaped loop and fold back on itself to form a bifurcated four chamber heart. With acquisition of air-breathing lungs in lungfish and amphibians, the heart has undergone separation of chambers to receive oxygenated blood from lungs and two sources of deoxygenated blood from the body. In fish the vessels of the circulatory system are organized in to the Fibonacci number of three (3) circulatory circuits: 1) from the heart to the gills and general body; 2) from the gills to the gut and liver and back to heart; and 3) from the gills to the tail and kidney and back to heart. The same three blood circuits are also retained in the birds and mammals with the lung loop replacing the gill loop [26]. In primitive vertebrates the brain consists of a single proencephelon (forebrain). This becomes subdivided in all later vertebrates in to the Fibonacci number of three (3) brain segments with the addition of the mesencephalon (midbrain) and the rhombencephalon (hindbrain). Emanting from the hind brain and spinal cord are a Fibonacci number of thirteen (13) cranial nerves, numbered 0 and I-XII. Each of these has dorsal and ventral roots that supply the various sensory organs of the body. The spinal cord extends the length of the body with dorsal (afferent) and ventral columns (efferent). These cell bodies send spinal nerve fibers out at each of the segmentally arranged vertebrae to supply the various organs and muscles of the body. The axial skeletal system of vertebrates consists of a backbone composed of variable numbers of vertebrae. In primitive vertebrate there is little regional variation except for caudal series bearing hemal arches ventrally and ribs may be present from neck to tail. In higher vertebrates the neck vertebrae (cervical) may or may not bear short ribs. The trunk (thoracic) region bears ribs, while short or absent ribs are located in the posterior lumbar series. The number of vertebrae is many and variable (maybe no one bothered to count them) in fish. In primitive amphibian, there were a total of 30 presacral vertebrae, a single sacral and a hundred or so caudal vertebrae. In modern amphibians such the frogs there are only 9 presacral, a fused rodlike urostyle representing a number of fused caudals. Primitive reptiles had 27 presacral vertebrae, two sacrals, and numerous caudals. In mammals there are uniformly 7 cervicals, and twenty or so dorsal (thoracic plus lumbar), and a variable number of shorter tail vertebrae. Unfortunately, the exact number of regional vertebrae for any given vertebrate order or species is usually not given.
11. CROSSOPTERYGIAN PECTORAL GIRDLE AND FIN BONES
Among ancient fossil fish, the crossopterygian fish were pre-adapted to making the transition from water to land by the possession of a series of shoulder (pectoral) bones with their associated bony appendages as depicted in Figure 15(a) [26]. The remarkable fact is the Fibonacci number of three (3) bones comprising the pectoral

Figure 15. A. Pectoral girrdle and fin bones of extinct fossil crossopterygian fish. B. Homologous pectoral bones of a tetrapod vertebrate. After Romer [26].
girdle (supracleithrum (scth), cleithrum (cth), and clavicle (cl)), and the Fibonacci number three (3) arm bones composed of medial proximal humerus (1), radius (r) and ulna (u) (2). Examination of the lateral distal arrangement of fin bones reveals a bifurcating series of the Fibonacci number of three (3) distal bones extending from the terminus of each larger proximal bone and the Fibonacci number of two (2) which are larger than the third (1), and in the next set of more distal bones this branching pattern alternates so that the third bone now bears the more distal two bones, while the previous two bones bear again repeats the more distal Fibonacci number of three (3) bones extend distally. This pattern of diminishing sized distal bones with their Fibonacci branching are the exact homologues of pectoral girdle and limb bones of all living tetrapod vertebrates (except for losses and specializations (see Figure 15(b)).
12. TURTLE ARMOUR
The ancient Chelonian order of living reptilian vertebrates are also the most heavily armoured of all land vertebrates The dorsal body or bony carapace consists medial series of the Fibomacci number of 8 neurals (includng one postneural), and Fibonacci number of 8 paired costals, surrounded laterally by a series of the Fibonacci number of 13 paired marginals (including the caudal pygal and frontal muchal). The ventral bony plastron consists of a series of the Fibonacci number of five (5) paired bony plates (epiplastron, endoplastron, hyoplastron, hypoplastron and xiphiplastron) [26].
13. HUMAN SKELETAL SYSTEM
A careful consideration of mammalian cervical vertebrae as represented by the human skeleton reveals, that of the seven cervical. Two vertebrae, that articulate with the skull, the axis and atlas, are differentiated from the five columnar vertebrae. The total count of 7 should really be separated into the two groups with the Fibonacci number of two (2) and five (5) cervicals, respectively. The thoracic region generally bears twelve ribs. However, there is often a thirteenth floating rib, giving the Fibonacci number of (13) total thoracic vertebrae. There is a Fibonacci number of five (5) sacral vertebrae, and an additional Fibonacci number of five (5) fused sacral vertebrae. The coccyx is composed of the Fibonacci numbers of three (3) to five (5) rudimentary vertebrae [27]. Given the inexactitude of the thoracic and coccygeal vertebrae count, the total count comes close to the Fibonacci number of thirty-four (34) vertebrae. The neural arch is itself composed of a neural spine and paired transverse processes which yield a branching Fibonacci number pattern of 5 processes. Even the 3 thoracic ribs are decomposed into 7 true ribs attaching directly to the sternum and the Fibonacci number of five (5) false ribs that attached to each other before attaching to the sternum. The sternum itself consists of the Fibonacci number of three (3) parts, a single manubrium with a single attached rib, a series of Fibonacci number of five (5) sternebrae and a ribless xiphisternum. These are all Fibonacci series numbers [28]. The pelvis is composed of a Fibonacci number of three (3) paired bones, the ilium, ischium and pubis. Most anatomist agree that the human skeletal system represents the unmodified less specialized condition of the mammals. The antiquity of this body plan for vertebrate limbs was presented above for the pectoral girdle of the crossopterygean fish. Finally, for dermal bones, the human dentition has a dental formula of two (2) incisor, one (1) canine, two (2) premolars, and three (3) molars in each half jaw. Once again these are all Fibonacci numbers, yielding a total Fibonacci number of eight (8) upper and lower jaw teeth [28]. A total Fibonacci number of thirty-four (34) teeth if we include two wisdom teeth.
14. DISCUSSION
According to Darcy Thompson [2] the appearance of Fibonacci numbers in biology is not due to some mysterious force. It can be accounted for by “the action of forces that lie in the steady production of similar parts, similarly situated, at similar successive intervals of time, and in consequence this gives rise to symmetrical patterns depending on the form of the entire surface.” We are in substantial agreement with this very general argument, and will elaborate in more detail later. For now, we provided ample observations demonstrating the ubiquity and generality of Fibonacci numbers across all levels of biological evolution. Our results document that Fibonacci numbers are found at virtually all hierarchical levels in the evolution and organization of life forms. For example, it has been noted that even at the very hereditary base, the DNA double helix is a prime example of a golden section with a pitch of 34 angstroms and width of 21 angstrom [29]. Moving up the evolutionary ladder, we provided examples of the occurrence of Fibonacci numbers at the sub-cellular and cellular levels of organization. The best documented case is the maternal inheritance and continued asexual perpetuation of corticotypes in the ciliate, Tetrahymena, that give rise to a stable modal Fibonacci number of twenty-one (21) kineties over hundreds of successive fissions. The body plan of Cuvier’s Radiata, the primitive diploblastic and unsegmented phyla (Coelenterates) and bilateral, acoelomate Platyhelminethes and Ashelmenthes) and other secondarily radially symmetrical animals (Echinoderms) also display the “Rule of Fibonacci Numbers.” Interestingly, it is the lower series of the Fibonacci numbers of three (3), five (5) and eight (8) that are the most predominant, and these numbers are apparent in their serially arranged appendages. These examples confirm that the occurrence of Fibonacci numbers is not limited simply to metameric and segmentally organized body plans. These are well documented here for annelids, crustacea and chordates in both larval and adults forms.
14.1. Epigenetics of Animal Segmentation
Segmentation of the animal body plan discussed earlier arises early in evolution. In metazoan embryology, we note the synchronous reiteration of undifferentiated cellular units during blastula stage. During gastrulation the colony of undifferentiated cells undergoes a series of asynchronous divisions and segregation of colonies occurs by staggered proliferation to forms a Fibonacci number of three (3) germ layers accompanied by invaginations and folding that shunt the reiterated and bifurcated clones in to preferred regions that undergo epigenetic determination and commitment to all of the differentiated types of tissues. Recently, the subject of animal segmentation has been studied in relation to regulation of specific gene expression and the so-called segmentation clock [30]. Theses authors posit that vertebrate somite formation, quoted as a total number of about 50, (or could it be closer to the Fibonacci number of fifty-five (55) somites), is a rhythmic process in zebrafish embryo, that may involve an underlying biochemical oscillator or segmentation clock driven by two developmental signaling genes, Wnt and Notch. They further posit that somehow the temporal oscillation is then converted in to a periodic spatial pattern of somite boundaries. Rhythmic expression begins during gastrulation and is maintained throughout somitogenesis. The existence of such a clock whose temporal periodicity can be translated spatially into periodic boundaries of somites was originally proposed in theoretical models [31]. We have proposed a similar biochemical anharmonic oscillator in cells [32] and as an explanation for the phenomenon of Fibonacci numbers in the development of staggered cell cycles during clonal growth of normal human epidermal keratrinocytes undergoing commitment to terminal differentiation [33]. The existence of cyclic genes in the segmentation clock has now been identified in fish, frog, chick and mouse embryos [34]. The generality of these periodic oscillations in all vertebrate is still unknown.
14.2. Occurrence of Fibonacci Sequence Numbers in HOX Gene Organization and Expression
The developmental program that defines the shape of vertebrae is controlled by HOX genes in somites [35]. The segmentation clock is thought to control spatiotemporal HOX gene activation, which play a role in determining the identity of the regional somites. Pourquie and Kumi [34] reported that a mutation of the Delta-like 3 gene in humans that is required for segment clock function, results in abnormal segmentation of the vertebral column as seen in the spondylocostal dysostosis syndrome.
We come now to the question of what, if anything, does the number of Hox genes and their clustering have to do with the number of body segments across the animal phyllogenetic spectrum. The number and presence of Hox genes in different animal phylum has been examined in many studies. The family of Hox genes vary from 4 to 48 per genome depending on the animal, and control of morphologies on the body axis in all metazoans, but in some cases clusters are fragmented [36]. As expected there are no Hox genes in non-segmented single celled protozoans. Nor are there any in the early diploblastic sponges (Porifera) and possibly none in the aberrant diploblastic sea comb Ctenophores. However, in true Coelenerates, Hox genes do play a role in axial patterning in Hydra [37], and there are eight Hox-like genes in the cnidarians, Nematostella, scattered over four different chromosomes with no apparent clustering nor any pattern of co-linear expression in development [38]. The triploblastic metazoans genomes contain a complement of Hox genes clustered together in contiguous chromosomal regions, and the spatial and temporal expression of these genes along the segmented body axis is regulated by the position of the genes from 3’ to 5’ direction along the chromosome, called co-linearity. As early as 1978, based on the number of homeotic mutations of the fruit fly, Drosphila, the body plan can be divided into eight distinct sections [39]. In fact, there is a cluster of exactly eight Hox genes that can be mapped in the same linear order as the eight anterior to posterior body regions regulated by these genes in both the larval and adult body [40]. In six other species of the Hexapoda, (Folsoma, Tribolium, Aaedes Schistocerca, Bombyx and Thermobia), there are a cluster of eight Hox genes corresponding to the body regions of Drosophila [41]. More remarkable is the presence in several orders of the phylum Arthropoda, of the same eight Hox genes clustering in the same order in six examined species of Crusacea (Artemia, Porcellio, Sacculina, Elminus, Trypetesa, and Urophysemia), five examined species of the Chelicerata (Archegozetes, Copiennius, Steatoda, Archeanarea, and the horsecrab, Limulus), and six examined species of the Myriapoda (Lithobius, Ethmostigmus, Stutigerilia, Pachymerium, Pauropus, and Acanthokara) [42]. A recent review [43], reported that the polychaete annelids had a Fibonacci number of five (5) Hox genes that are expressed in a staggered overlap pattern along the anterior-posterior axis corresponding to the A1 to A9 segments. In a more detailed genetic analysis of the annelid, Platynereis, there are three defined body segments and a corresponding Fibonacci number of three (3) Hox genes (Hox 1, hox 4, and hox 5) [44]. These authors reported that the first discernable segmental entity in the annelid P. dumerilli that is delineated by a stripe of engrailed geneexpressing cells. In the segmented arthtropods, the fruit fly Drosphila expresses the Fibonacci number of eight (8) Hox genes (lab, pb, Dfd, Scr, Antp, Ubx, abd-A, and Abd-B), which are expressed in overlapping segments that stretch along the anterior-posterior body axis in both the larva and adult body plan possessing the Fibonacci number of thirteen (13) metameric segments corresponding to the combined thoracic and abdominal body segments. In vertebrates Hox gene complex governs both overt and non-overt segmentation [45]. Again, the temporal and spatial expression of Hox genes reflect their anterior-posterior readout in the vertebrate body plan and is largely co-linear with chromosomal location The thirtynine genes of the Hox complex comprises four distinct Hox gene complexes (Hox A, B, C, and D) that are organized into the Fibonacci number of thirteen (13) homology or paralogue groups. Nine of the thirteen of the paraloques all seem to be derived from the Abd-A gene through some gene duplication event. In the primitive chordate, Amphioxus, there is only the Fibonacci number of one (1) complex, the Hox A cluster. Among the four clusters there has been considerable gene loses. Elasmobrach (sharks bats) or cartilaginous fish are missing the Hox C cluster [46]. Unlike in Drosophila where the single Hox A cluster is expressed all at the same time (in a syncytium) during gastrulation the mouse Hox complex is temporally co-linear, meaning that the body plan develops in an anterior-posterior direction [47]. The mouse genome expresses the Fibonacci number of thirteen (13) Hox genes (a1-a13). During mouse embryo development the last three segments of the hindbrain are associated with the Fibonacci number of three (3) Hox genes (hoxb, hoxc, and hoxd), and along the anterior-posterior axis there is a correspondence between somite arrangement proceeding from anterior to posterior in four groups of the Fibonacci number of three (3) segments, that are associated with four Hox genes (hoxd, hoxe, hoxf and hoxg), followed by a groups of the Fibonacci number of eight (8) somite segments, that are associated with the expression of only the Fibonacci number of one (1) Hox gene (hoxh), and finally the tail segment is composed of the Fibonacci number of thirteen (13) somites and the expression of only one reiterated Hox gene (hoxi). An interesting insight into the question of Fibonacci number of segments and Hox gene expression is the observation, that HoxC6 is expressed at the cervico-thoracic junction in mouse, chicken, goose, the amphibian, Xenopus, and zebrafish, even though they have different numbers of cervical vertebrae. This apparent detour into Hox gene number, expression and animal segmentation has shown that the Hox genes are themselves subject to the Rule of Fibonacci Numbers, but they do not determine the number of body segments in bilateral animal phyla. They merely determine what genes will be turned on in those segments. The origin of body segmentation in the earliest protosomeans appear to be in a common ancestor of annelids/arthopoda (Lochotrochophorans). One theory is that a radially symmetrical ancestor of this group adopted the anterio-posterior axial patterning by extending from a radial symmetrical head region along a preferred meridional axis, that of the larger “D” blastomere, that arises during spiral cleavage in the phylogenetic ancestor of the spiralia [48].
14.3. Fibonacci Paradigm for Stem Cell Fates Based on Clonal Growth Dynamics
We postulate that there is a one-to one correspondence relating the Rule of Fibonacci Numbers to the rules governing clonal growth of human epidermal stem cells Table 1).
A particular example of this correspondence was reported earlier [33]. A proliferating normal human clone of epidermal keratinocytes committed to terminal differentiation adopts a pattern of division in which two different branches of the binary division tree diverge with one of the two daughter cells at each nodal division time dividing on time, while its sister cells fails to divide, but resumes division exactly one cycle later (Modulo 1). Then, at the next cell cycle, the first branch fails to divide on time, but divides again at the next nodal division cycle (modulo 2). This alternating pattern of cell division gives rise to a Fibonacci numbers in the total number of cells at each binary division node (see Figure 16).
The graph shows that by day 8 of clonal growth clone 15 terminated growth with the Fibonacci number of

Table 1. Fibonacci rabbit paradigm for stem cells.

Figure 16. Fibonacci pattern in growth of 15 clones of keratinpocytes undergoing commitment to terminal differentiation. After Wille [33].
twenty-one (21) cells. If all cells had divided every day as do their synblastic cloned cells that divide once every day, there should be 64 cells. Likewise, clones 2 and 3, terminated division on day eight with the Fibonacci number of thirteen (13) cells. One clone terminated on day eight of culture with the Fibonacci number of five (5) cells. Clones numbered 13, 29, and 36 terminated division on day 8 of culture with the Fibonacci number of three (3) cells, two clones 20 and 27 terminated division with the Fibonacci number of two (2) cells after eight days of culture, and finally after eight days five clones numbered 1, 22, 25, 30, and 34 terminated division without ever dividing with the Fibonacci number of one (1). Fourteen of the fifteen (93%) of “committed” keratinocyte clones that were unable to divide at least once a day ceased division with a Fibonacci number of total cells after eight days of culture and achieved at best less than three binary cell divisions. This pattern of clonal expansion can be modeled as a self-similar Fibonacci recursive transitional network (RTN) diagram [7] as depicted in Figure 17.
The Fibonacci pattern of cell growth is an example of a recursive nodal pattern of staggered binary cell division in differentiation of committed epidermal keratinocyte clones. Here, a single progenitor cell generates two daughter cells, both of which retain the binary code of division but only express it in one member of the pair alternately at each successive cell division.
14.4. Generalization of Fibonacci Growth Patterns in Vertebrate Skeletal Development
The number and arrangement of bones of the vertebrate axial skeleton provide additional evidence for the Fibonacci pattern of a triad of bones that display a self-similar pattern of one proximal bone that is followed distally by two bones one of which is always larger than the other as shown in Figure 15 for the crossopterygian pectoral girdle and forelimb bones. In the crossopterygian as in all tetrapod pectoral girdle, there is the Fibonacci number of three (3) bones. The most proximal is the largest, the supracleithrum and the cleithrum in tetrapods. These are followed distally by two bones the larger cleithrum and the smaller, the clavicle. The antiquity of this body plan for vertebrate limbs as presented

Figure 17. Fibonacci sequence diagrammed as recursive transitional network (RTN). After Hofstadter [7].
above for the pectoral girdle of the crossopterygean fish, carries over to the homologous tetrapod pectoral girdle bones. The triad of three bones are the larger clavicle and the smaller interclavicle and clavicle. This triad bone pattern is repeated distally by the proximal large humerus bone followed distally by two bones, the larger radius and the smaller ulna in both the crossopterygian and all tetrapods. This triad bone pattern is repeated more distally in the crossoptertygian fin bones with three bones distal to the radius, one of which is larger medially than the two smaller bones positioned laterally. The smaller ulna gives rise distally to two bones; the larger medial one and a smaller lateral one. Together, the ulna and its two distal bones make a repeated and self-similar triad just like the immediately proximal triad of the humerus, radius and ulna. A schematic diagram of this self-similar “nested triad” of bones is presented in Figure 18.
The blue box contains at a single unpaired lateral humerus bone, H(l); coded by the encircled Fibonacci numbers 2 and 3 (red box) because it is an a proximal unpaired bone. This is interpreted developmentally as modal cycle delay prior to clonal bifurcation in to more distal descendants, the smaller lateral ulna, U1(l), coded by the encircled Fibonacci number 4, and the larger medial radius, R1(m), coded by the encircled Fibonacci number 5. These three bones constitute of bones of Triad I. The dark salmon colored box contains the larger proximal radius, R1(m), coded by the encircled Fibonacci numbers 5 and 8 (red box), which again is interpreted as a modal delay prior to clonal bifurcation to its more distal descendants, the larger medial R2(m), encoded by the encircled Fibonacci numbers 13 and 21 (red box), and the smaller lateral bone, R3(l), encoded by the Fibonacci number 12. These three bones form the self-similar bones of Triad II. The bone R3 (l), coded by the encircled Fibonacci number 12, bifurcates to form the two most distal bones, R4(l), coded by the Fibonacci number 19 and R5(m), coded by the Fibonacci encircled number 20. Together with R3(l) these three bones form the self-similar bones of Triad IV. Now turning to the more distal descendants of U1(l), are the medial bone, U2(m), coded by the Fibonacci number 7 and 11 together with the lateral bone U3(l), coded by the Fibonacci encircled number 6; they form the self-similar three bones of Triad II (light green box). Again, U2(m) is the larger of the two bones enclosed in the dark green box represented by the Fibonacci encircled numbers 7 and 11. The distal descendants of the larger U2(m) form the selfsimilar Triad V; they are the medial and lateral smaller distal bones encoded by the encircled Fibonacci numbers 17 and 18, respectively. Finally, we come to the distal descendants of U3(l), which bifurcates in to the larger medial U6(m) bone, coded by the encircled Fibonacci numbers 10 and 16 enclosed in dark green box, and the distal descendants of the smaller U5(l) bone , coded by the Fibonacci encircled number 10, which itself bifurcates in to a lateral U7(l) and a U8(m) pair of bones, coded by the encircled Fibonacci numbers 14 and 15, respectively. Together U5, U6 and U7 form the three bones of Triad VI (dark blue box). It should be noted that the medial Triad II and the lateral Triad IV are mirror images of the lateral Triad II, and lateral Triad VI. This two-fold rotational symmetry may reflect the bilateral organization of the developmental pathways that regulate the patterning of bones progressing from their proximal origins to their distal endpoints. The same evolutionarily conserved Fibonacci series of bones forming a triad pattern of self-similar bones is found in the pelvic girdle and associated limb bones of all tetrapods, the details of which are left to the reader to document.
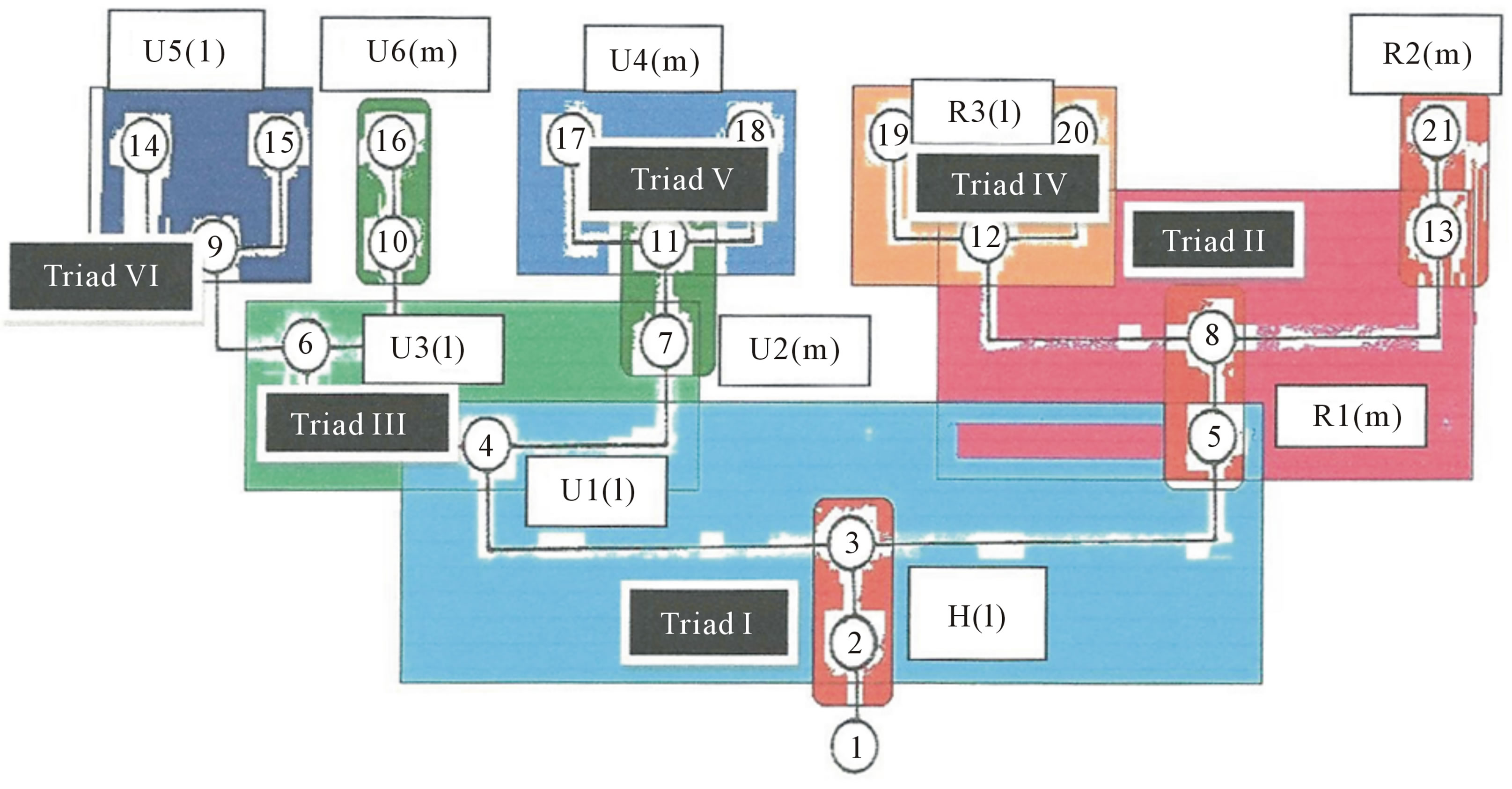
Figure 18. Fibonacci recursive network pattern of nested triads of bones of the crossopterygian pectoral fin.
14.5. Examples of Fibonacci Triad Bone Patterns in Humans
The human hand has the Fibonacci number of eight (8) carpals grouped so that the Fibonacci number of three (3) carpal bones are positioned just distal to the radius, the larger medial scafoid bone, and the smaller lateral lunate bone [27]. Just distal to the smaller ulna is the single pisiform carpal bone. More distal, are a group of the Fibonacci number of five (5) carpals, the medial trapezium and trapezoid bones making a triad with the scaphoid bone. The remaining three distal carpal bones are the lateral triangular and hamate and the medial, capitate. The carpals are extended distally to the Fibonacci number of five (5) metacarpals. A repeated self-similar triad is formed of the most lateral carpal, the hamate with the fourth and fifth later metacarpals. A triad is formed between the two medial carpals, the capitate and trapezoid with a single medial metacarpal. While the most medial carpal, the trapezium, forms a triad with the smaller lateral thumb bearing metacarpal and the larger index finger bearing metacarpal. Thus, repeating the more proximal triads as a self-similar Fibonacci pattern of bones. The Fibonacci number of five (5) phalanges bears the Fibonacci number of two (2) digits on the thumb and the Fibonacci number of three (3) digits on the remaining fingers. They all display ratios of bone sizes of the digits from larger proximal to distal joints that are the Golden Section.
In summary, a similar analysis for the human axial hind limb bones as that carried out above for the forelimb bones would yield the same pattern of bifurcating triads of bones with a single proximal bone, in this case, the femur bifurcating in to two distal bones al larger tibia and a smaller fibula bone. The significance of this Fibonacci arrangement of medial and lateral bones extending from proximal to distal direction is a reflection of the underlying self-similarity of triads composed of one large and two small bones, that explains an embryological mechanism of clonal growth and tissue determination that follows the Fibonacci cell division pattern discussed above as the recursive transition network model for clonal growth and commitment to terminal differentiation. It is our hypothesis that this staggered and alternating pattern of clonal growth is a fundamental biological rule underlying embryonic development, and is responsible for the prevalent occurrence of Fibonacci numbers witnessed in their phylogenetic appearance in much of animal embryonic and adult structures reviewed here. We also interpret the occurrence of Fibonacci numbers associated with animal segmentation as a consequence of clonal bifurcation that sets the permissible boundaries and are the clues to where nodal clonally and tissue determination decision points are destined to occur.
In agreement with this concept, it has been reported that mutations which affect the number of cell division occurring during early development alter the number of somites. Whatever, the exact role of cycle genes are that set clonal division boundaries will have to await further dissection of developmental events that are associated with clonal division mechanics as proposed here, and schematically diagrammed by the hypothetical dendrogram of committed epidermal keratinocyte clones [33]. In summary, our survey of zoological literature has affirmed the wide occurrence of Fibonacci numbers in the organization of acellular and prokaryotic life forms as well as in some eukaryotic protistans and in the embryonic development and adult forms of many living and fossil remains of metazoan animals. A detailed comparative analysis of the axial skeleton of fossil fish and humans revealed a new rule of the “nested triad” of bones organized along the proximal to distal axis of limb appendages. This growth pattern and its ubiquity among living vertebrates appear to underlie a profound rule of pattern formation t.hat is dictated in part by the genetics and epigenetic mechanisms of stem cell clonal development.
REFERENCES
- Cook. T.A. (1979) The curves of life. Dover Publications, Inc., New York.
- Thompson, D.W. (1943) On growth and form. Cambridge University Press/The MacMillan Company, New York.
- Weyl, H. (1952) Symmetry. Princeton University Press, Princeton.
- Livio, M. (2002) The golden ratio. Broadway Books, New York.
- Douady, S. and Couder, Y. (1992) Phyllotaxis as a physiccal self-organized process. Physical Review Letters, 68, 2098-2101. doi:10.1103/PhysRevLett.68.2098
- Stewart, I. (2011) The mathematics of life. Basic Books, New York, 49.
- Hofstadter, D.R. (1980) Goedel, Escher, Bach: An eternal braid. Vintage Books, New York.
- Schroeder, M. (1991) Fractals, Chaos, power laws. W.H. Freeman and Company, New York.
- Gleick, J. (1987) Chaos: Making a new science. Penguin Group, Viking, New York.
- Goodard, T., Huang, C. and Ferrin, T. (2004) New approaches for visualizing virus capsids. NCRR Principle Investigator Meeting, June 2004. http://www.cgl.ucsf.edu/Research/virus/poster/poster.html
- Liu, C., Fu, X., Lui, L., Ren, X., Chau, C.K.L., Li, S., Xiang, L., Zeng, H., Chen, G., Tang, L.-H., Lenz, P., Cui, X., Hunag, W., Hwa, T. and Huang, J.-D. (2011) Sequential establishment of stripe patterns in an expanding cell population. Science, 314, 238-241. doi:10.1126/science.1209042
- Bees M.A. and Hill, N.A. (1997) Wavelengths of bioconvection patterns. The Journal of Experimental Biology, 200, 1515-1526.
- Chatton, E. and Lwoff, A. (1930) Silver stain technique. Comptes Rendus Social Science Biologie Filiales, 104, 831-836.
- Williams, N.E. (2004) The epiplasm gene EPC1 influences cell shape and cortical pattern in Tetrahymena thermophilia. Journal of Eukaryotic Microbiology, 51, 201- 206. doi:10.1111/j.1550-7408.2004.tb00546.x
- Nelson, E.M. and Frankel, J. (2005) Regulation of corticotype through kinety insertion in Tetrahymena. Journal of Experimental Zoology, 210, 277-287. doi:10.1002/jez.1402100211
- Frankel, J. (1980) Propagation of cortical differences in Tetrahymena. Genetics, 94, 607-623.
- Nanney, D. (1966) Corticotype transmission in Tetrahymena. Genetics, 54, 955-968.
- Kaczanowska, J. and Dubielecka, B. (1983) Pattern determination and pattern regulation in Paramecium tetraurelia. Journal of Embryology & Experimental Morphology, 74, 47-68.
- Klindworth, T. and Bardele, C.F. (1996) The ultrastructure of the somatic and oral cortex of the karyorelictean ciliate Loxodes. Acta Protozoologica, 35, 13-28.
- Borradaile, L.A., Potts, F.A., Eastham, L.E.S. and Saunders, J.T. (1958) The invertebrata. 3rd Edition, Cambridge University Press, Cambridge.
- Ehret, C.F. (1967) Paratene theory of the shapes of cells. Journal of Theoretical Biology, 15, 263-272. doi:10.1016/0022-5193(67)90207-X
- Potter, G.E. (1947) Textbook of zoology. 2nd Edition. The C.V. Mosby Company, Saint Louis.
- http://www.wikipedia.com/caenorhabditis
- Scott, R. (2003) Darwin and the barnacle. W.W. Norton & Company, New York.
- Wille, J.J. Survey of Pecten shells collected at Atlantic Highlands, NJ.
- Romer, A.S. (1956) The vertebrate body. W.B. Saunders Company, Philadelphia.
- Hartenstein, R. (1976) Human anatomy & physiology: Priniciples and applications. D. Van Nostrand Company, New York.
- Hyman, L. H. (1942) Comparative Vertebrate Anatomy. 2nd Edition. The University of Chicago Press, Chicago.
- www.goldennumber.net/dna/htm
- Pourquie, O. (2003) The segmentation clock: Converting embryonic tissue time into spatial pattern. Science, 301, 328-330. doi:10.1126/science.1085887
- Cooke, J. and Zeeman, E.C. (1976) A clock and wavefront model for control of the number of repeated structures during animal morphogenesis. Journal of Theoretical Biology, 58, 455-476. doi:10.1016/S0022-5193(76)80131-2
- Kauffman, S.A. and Wille, J.J. (1974) The mitotic oscillator in Physarum polycephalum. Journal of Theoretical Biology, 55, 47-93. doi:10.1016/S0022-5193(75)80108-1
- Wille, J.J. (2011) Growth dynamics of individual clones of normal human keratinocytes: Observations and theoretical considerations. Natural Sciences, 3, 702-722. doi:10.4236/ns.2011.38094
- Pourquie, O. and Kusumi, K. (2001) When body segmentation goes wrong. Clinical genetics, 60, 409-416. doi:10.1034/j.1399-0004.2001.600602.x
- Kmita, M. and Duboule, D. (2003) Organizing axes in time and space: 25 years of collinear training. Science, 301, 331-333. doi:10.1126/science.1085753
- Lemons, D. and McGinnis, W. (2006) Genomic evolution of Hox gene clusters. Science, 313, 918-1922. doi:10.1126/science.1132040
- Irvine, S.Q. and Matindale, M.Q. (2001) Comparative analysis of hox gene expression in the polychaete Chaetopterus: Implications for the evolution of body plan regionalization. American Zoologist, 41, 640-651.
- Myers, P.Z. http://scienceblogs.com/pharyngula/2006/05/jellyfish
- Brady, G. (2000) Hox genes: The molecular architects. The Irish Scientist Year Book. www.ireland.com/newspaper/science/2000/065/sci.htm.
- Dawkins, R. (2004) The ancestor’s tale: The dawn of evolution. A Mariner Book: Houghton Mifflin Company, Boston, New York, 418-424.
- Myers, P.Z. (2006) Jellyfish lack true Hox genes! http://scienceblogs.com/pharyngula/2006/05/jellyfish_lack_true_hox_genes.php
- Myers, P.Z. (2004) A brief overview of HOX genes. http://scienceblogs.com/pharyngula/2004/brief_overview_of_hox_genes
- Carroll, S. Grenier, J.K. and Weatherbee, S.D. (2001) From DNA to diversity: Molecular genetics and the evolution of animal design. Blackwell Scientific, Maiden.
- Steinmetz, P.R., Kostyuchenko, R.P., Fischer, C. and Arendt, D. (2011) The segmental pattern of otx, gbx, and HOX genes in the annelid Platynereis dumerilli. Evolution & Development, 13, 72-79. doi:10.1111/j.1525-142X.2010.00457.x
- Rancourt, D. (1998) Establishment of spatial patterns of gene expression during early vertebrate development: HOX genes. http://ucalgary.ca/uofc/eduweb/virtualembryo/hox.hml
- King, B.L. Gillis, J.A., Carlisle, H.R. and Dahn, R.D. (2011) A natural deletion of the Hox C cluster in elasmobrach fishes. Science, 334, 1517.
- Browder, L.W., Erickson, C.A. and Jeffery, W.R. (1991) Developmental biology. 3rd Edition, Saunders College Publishing, Philadelphia.
- Shankland, M. and Seaver, E.C. (2000) Evolution of the bilateral body plan: What have we learned from annelids. Proceedings of the National Academy of Sciences, 97, 4436-4437. doi:10.1073/pnas.97.9.4434

