Health
Vol.10 No.11(2018), Article ID:88606,22 pages
10.4236/health.2018.1011115
Empirical Studies of Effects of High Blood Pressure on Medical Costs and Heart Disease: Is the 2017 ACC/AHA Guideline Supported by Enough Evidence?
Kazumitsu Nawata1, Moriyo Kimura2
1Graduate School of Engineering, University of Tokyo and Research Institute of Economy, Trade and Industry (RIETI), Tokyo, Japan
2The Public Health Institute, Tokyo, Japan

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 7, 2018; Accepted: November 17, 2018; Published: November 20, 2018
ABSTRACT
Background: The American College of Cardiology (ACC), American Heart Association (AHA) and other organizations announced a new hypertension guideline in November 2017. However, previous studies have pointed out that this new guideline might lack sufficient evidence to justify its use. Data and Methods: The effects of blood pressure (BP) on medical costs and on the probability of having heart disease as anamnesis are analyzed. We used a dataset containing 175,123 medical checkups and 6,312,125 receipts from 88,211 individuals obtained from three health insurance societies from April 2013 to March 2016. The dataset was divided into subgroups based on whether the patients had diabetes and took hypertension medications. The power transformation and probit models were used in the study. Results: We observed negative effects of systolic BP (SBP) on medical costs in most subgroups. We could not find evidence that higher SBP made the medical costs and probability of having heart diseases higher. The results raise uncertainty about the reliability of the new guideline, at least for SBP. Conclusion: The results of this study did not support the new 2017 ACC/AHA guideline, at least for SBP. The new guideline must be more carefully reevaluated by additional studies. Limitations: The dataset was observatory, the sample period was only 3 years, and we could not complete a time-series analysis of individuals.
Keywords:
2017 ACC/AHA Hypertension Guideline, Hypertension, Blood Pressure, Medical Costs, Cardiovascular and Heart Disease

1. Introduction
The American College of Cardiology (ACC), American Heart Association (AHA), and other organizations published the “2017 ACC/AHA/AAPA/ABC/ACPM/ AGS/APhA/ASH/ASPC/NMA/PCNA Guideline for the Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults” (hereafter, the 2017 ACC/AHA guideline) [1] [2] [3] in November 2017. It was the first revision of the high blood pressure (BP) or hypertension clinical practice guideline [3] since the “Seventh report of the joint national committee on prevention, detection, evaluation, and treatment of high blood pressure (JNC 7)” [4] [5] in 2003. Under the new guideline, the threshold for hypertension requiring treatment with lifestyle changes and hypertension medication is 130/80 mmHg. The 2017 ACC/AHA guideline replaces the term “pre-hypertension” with “elevated BP” (systolic BP (SBP) of 120 - 129 mmHg and diastolic BP (DBP) below 80 mmHg). In this guideline, “stage 1 hypertension” is defined as SBP of 130 - 139 mmHg or DBP of 80 - 89 mmHg, and “stage 2 hypertension” is defined as SBP corresponding to stages 1 and 2 in the JNC 7 report (SBP of 140 mmHg or more, or DBP of 90 mmHg or more).
As a result, the prevalence of hypertension among US adults substantially increases from 32% under the JNC 7 criteria to 46% under the criteria of the new guideline. Nonetheless, the guideline states that [1] “the new definition results in only a small increase in the percentage of US adults for whom antihypertensive medication is recommended in conjunction with lifestyle modification.” The 2017 ACC/AHA guideline is an official policy of the ACC and AHA. The focus is on medical practice in the US, but the guideline is expected to have a global impact, as the authoring institutions have stated. Indeed, the influence of the new ACC/AHA guideline is so large that careful reviews of various studies and the performance of further studies are absolutely necessary to determine whether or not the new guideline is appropriate.
The American Academy of Family Physicians, an organization that joined the initial announcement, declared that they would not endorse the 2017 ACC and AHA guideline and would continue to endorse the JNC 7 guideline [6] because the new guideline was not grounded in an assessment of the background resources; that is, substantial weight was given to the Systolic Blood Pressure Intervention Trial (SPRINT) [7] , but other trials were minimized.
In the SPRINT, 9361 participants with SBP of 130 mmHg or higher and an increased cardiovascular risk, but without diabetes, were randomly assigned to two groups. One was the standard treatment group (SBP target of less than 140 mmHg, 4683 participants) and the other was the intensive treatment group (SBP target of less than 120 mmHg, 4678 participants). The trial period was from November 2010 to March 2013, and the trial was stopped early after a median follow-up of 3.26 years owing to a significantly lower rate in the intensive treatment group. However, this might raise the possibility of end-point or termination biases [8] . Their results showed lower rates of fatal and nonfatal major cardiovascular events and death from any course in the intensive treatment group than in the standard treatment group. However, the SPRINT was not a blinded randomized clinical trial (RCT). Both doctors (or researchers) and participants could easily have awareness of the subject groups. Thus the placebo effect [9] [10] might have affected the outcomes of the trials. The mortality rates from any cause were similar for both groups in the first two years and the number of participants declined after the third year. Moreover, the Action to Cardiovascular Risk in Diabetes (ACCORD) Study Group [11] performed a similar trial with 4733 participants with type 2 diabetes. (The SPRINT used a framework similar to that of the ACCORD.) Unlike the SPRINT, the ACCORD showed that targeting SBP below 120 mmHg did not reduce the rate of composite outcomes of fatal and major nonfatal major cardiovascular events compared to targeting SBP below 140 mmHg.
Lewington et al. [12] performed a meta-analysis of individual data for 1,000,000 adults in 61 prospective analyses. They studied 12.7 million person-years at risk. They identified about 56,000 cases of vascular death, including 12,000 stroke, 34,000 ischaemic heart disease (IHD), and other vascular deaths. They found that IHD mortality increased in all age cohorts (from 40 - 49 to 80 - 89) as SBP and DBP increased. The selection criteria of 61 studies used in the meta-analysis were not clarified. As pointed out by Nawata Sekizawa and Kimura [13] , biases such as publication [14] [15] biases and conflicts of interest [16] might have existed, and the results could have been affected by such biases even if all studies were proper RCTs. Moreover, BP levels were strongly affected by various factors such as the age, gender, health conditions, and lifestyles of the individuals. Race, genetic and environmental factors, and health administrative activities are also important factors for BP [17] [18] [19] . However, the methods used to adjust for the effects of individual characteristics in the various studies are not clear. Nawata et al. [20] found that SBP increased about 5 mmHg with 10 years of increased age. The 10-year age cohort interval might have been too long, and some effects of the ages of individuals might have remained. These facts raised questions about the conclusions of the analysis.
Rapsomaniki et al. [21] used the linked electronic health records of 1.25 million patients in the CALIBAR (CArdiovascular research using LInked Bespoke studies and Electronic health Records) program in the UK from 1997 to 2010. During a median follow-up of 5.2 years, 83,098 initial cardiovascular disease (CVD) cases were reported. They concluded that people at age 30 with hypertension had a lifetime risk of overall CVD of 63.3%, compared with 46.1% for those with normal BPs, and developed CVD 5.0 years earlier. In the CALIBAR program, patients were linked across four clinical data sources. However, a crucial limitation of the study design is that only clinical sources were used. Healthy individuals, who did not go to any clinics or hospitals during the sample periods, were not included. Therefore the sample selection biases pointed out by Heckman [22] would be a problem, and it might not be appropriate to apply the results to the general public, including healthy people who were not included in the survey, even if the number of observations was large. (For details, see the appendix.)
Muntner et al. [23] analyzed data for 10,907 participants from the 2011-2012 and 2013-2014 cycles of the US National Health and Nutrition Examination Survey (NHANES) of adults. They mentioned that implementation of the 2017 ACC/AHA hypertension guideline would increase the use of hypertension medications, and also should reduce CVD events. Although some characteristics and health conditions of the participants were considered, “obesity,” a very important variable affecting health conditions, was not included in their analysis, as pointed out by Nawata and Kimura [24] .
Nawata and Kimura [24] analyzed the relationships between medical costs and BP. They found that the simple correlation coefficient of medical costs and SBP was positive, but the sign of the SBP estimate became negative when a variable representing obesity was included. Their results raise a question about the reliability of the 2017 ACC/AHA guideline. However, there were some incomplete aspects of their study. For example, the dataset included both diabetic and non-diabetic individuals. SPRINT used a dataset without diabetes, and ACCORD used type 2 diabetic patient data. Therefore, this discrepancy might have affected the results of the study. In addition, some individuals were taking hypertension medications, and hypertension medications make medical costs higher and BP levels lower. Therefore, this fact might have affected the results of the analysis. Moreover, while they analyzed the medical costs, the risks of CVD and heart disease (hereafter, CVD/ HD) were not analyzed.
The present paper is thus the first to analyze the effects of BP (especially SBP) on annual medical costs with consideration for the effects of diabetes and hypertension medications. Diabetes is classified as type 1 or 2, with 90% or more of all diabetic cases being classified as type 2 [25] [26] [27] . Since classifying types is difficult in adults [28] [29] , and the type of diabetes is not reported in many cases, we did not separate type 1 and type 2 diabetes. The dataset was divided into subgroups on the basis of having diabetes or not and taking hypertension medications or not. The medical costs were analyzed using the power transformation tobit model. Then the probabilities of having CVD/HD as anamnesis were analyzed using the probit model. The dataset contains 175,123 medical checkups and 6,312,125 receipts obtained from 88,211 individuals for 3 fiscal years (fiscal years 2013 to 2015; April 2013 to March 2016).
2. Data and Methods
We used an anonymized dataset combining medical checkups and receipts. We analyzed the effects of BP levels (especially SBP) on annual medical costs using subgroups of the dataset. Since SPRINT and ACCORD used patient data classified according to the presence or absence of diabetes, we first divided the dataset into two groups; one consisted of individuals who had diabetes as anamnesis or were judged by doctors to have diabetes at medical checkups (hereafter, the diabetic group), and the other consisted of those did not have diabetes (the non-diabetic group). The effects of BP on medical costs were analyzed separately for each group. Secondly, the dataset was divided into two groups based on whether individuals were taking hypertension medications (medication group) or not (non-medication group), and their medical costs were analyzed. Finally, the risks of CVD/HF were analyzed. Although the subjects were prescribed different types of hypertension medications [30] [31] [32] [33] , we did not consider the types of hypertension medications in this study.
Since medical costs take many zero values, and their distribution has a very heavy tail, the power transformation tobit model [34] was used for the medical cost analysis. The probability of CVD/HD risk was then analyzed by the probit model.
2.1. Data
Japan has a public health insurance system that requires all citizens to belong to some type of public health insurance organization. Corporations form health insurance societies for employees and their family members. Most employees 40 years of age or older must undergo medical checkups once a year by law [35] , and family members can also undergo medical checkups on a voluntary basis. The dataset was created with the cooperation of three such health insurance societies (Societies 1 - 3) and participants were all members and their family members of the health insurance societies who underwent medical checkups during the sample period.
Society 1 was an organization formed by a large Japanese company with offices and operational centers throughout Japan. Societies 2 and 3 were organizations formed by groups of smaller corporations. The dataset contained information regarding 175,123 medical checkups from 88,211 individuals between fiscal years 2013-2015 (the Japanese fiscal year begins in April and ends in March of the next year). At the medical checkups, individuals were asked if they were taking hypertension medications or not in all three societies and if they had CVD/HD as anamnesis in Societies 1 and 2.
The monthly reports of medical treatments and payments are called “receipts”. Receipts were classified into five categories: dental; inpatients of DPC hospitals; outpatients and inpatients of non-DPC hospitals; and pharmacies. All receipts are sent from medical institutes, such as hospitals, clinics, and pharmacies, to the health insurance associations. Payments are made to the medical institutes after the receipts are checked. In this study, the sum of the DPC, outpatient and non-DPC hospital, and pharmacy receipts was used to represent the medical costs.
Japan measures medical expenditures in points, and 10 yen per point has been paid to hospitals since 1958 [36] . In the present analysis, we summed a total of 6,312,125 receipts, and calculated the medical costs of individuals in each fiscal year. We used a dataset containing 175,123 cases for which both the results of checkups and medical costs were available in the same fiscal year. For details of the dataset see Nawata and Kimura [24] .
2.2. Power Transformation in Tobit and Probit Models
Since medical expenditures take many zero values, and their distribution has a very heavy tail, the power transformation tobit model [34] is used in the analysis of medical costs. The model is given by
(1)
where Mi represents the medical payments of the i-th individual, is the transformation parameter that makes the distribution close to the normal distribution, and is a latent variable whose value is not observable when it is negative. is a vector of explanatory variables, is a vector of unknown parameters, and is an error term following the normal distribution with a mean of 0 and a variance of . We consider the following power transformation tobit model in Equation (1).
(2)
The explanatory variables used in Equation (2) are as follows: Age, Female (1: if female; 0: otherwise), Height (cm), BMI (=weight (kg)/height (m)2), SBP and DBP (mmHg), HDL (high density lipoprotein cholesterol blood, mg/dL), LDL (low-density lipoprotein cholesterol, mg/dL), Triglyceride (mg/dL), GGP (γ-glutamyl transferase, units per liter: U/L), AST (aspartate aminotransferase, U/L), ALT (alanine aminotransferase, U/L), Blood_sugar (mg/dL), Urine_sugar (integers of 1 - 5, sugar in urine increasing with number; 1 is normal, 5 is worst), Urine_protein (same as Urine_sugar), F_year14 (1: fiscal year 2014; 0: otherwise), F_year2015 (1: fiscal year 2015), Society 2 (1: Society 2; 0: otherwise), and Society 3 (1: Society 3; 0: otherwise). For the details regarding these variables, see Nawata and Kimura [24] .
Let be a dummy variable taking 1 if an individual had CVD/HF as anamnesis and 0 otherwise. The probit model is given by
(3)
if and if and
where is the probability that , follows the standard normal distribution, and is its distribution function. is another latent variable, and only its sign is observable. The information in the following equation is used in the probit analysis (CVD/HD was not available for Society 3).
(4)
3. Results of Analysis
3.1. Distributions of Medical Costs
3.1.1. Diabetic and Non-Diabetic Groups
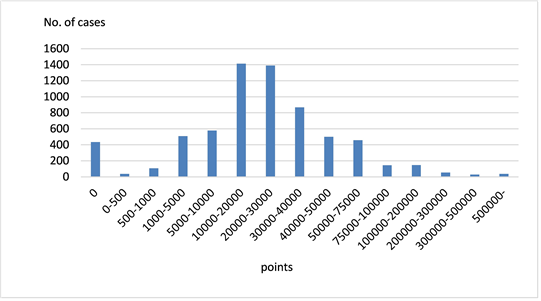
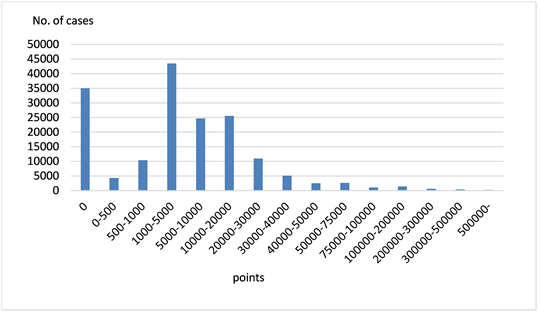
Figure 1 and Figure 2 show the distributions of medical costs for the diabetic and non-diabetic groups. The diabetic and non-diabetic groups contained 6708 (3.8%) and 16,415 (96.2%) cases, respectively. The distributions are skewed and have very heavy tails on the right side, especially in the diabetic group. The basic statistics (points) are a mean of 33,031, a median of 21,631, and a standard deviation (SD) of 59,894 for the diabetic group; and a mean of 12,572, a median of 3769, and a SD of 37,870 for the non-diabetic group. In 6.5% and 20.8% of cases in the diabetic and non-diabetic groups, respectively, the medical costs were zero. The mean medical cost of the diabetic group was 2.6 times as much as that of the non-diabetic group.
3.1.2. Hypertension Medication and Non-Medication Groups
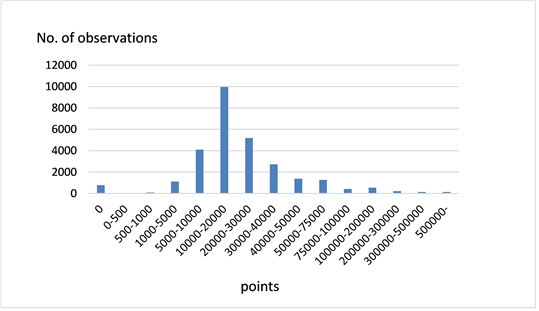
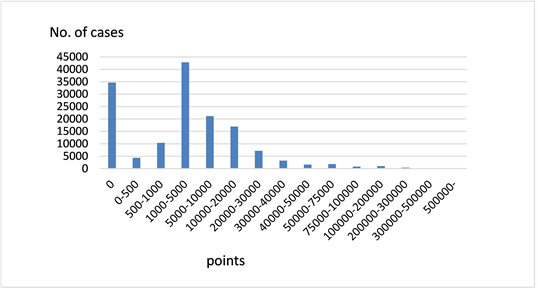
Figure 3 and Figure 4 show the distributions of the medical costs of the hypertension medication and non-medication groups. The numbers of cases in the medication and non-medication groups were 28,060 (16.0%) and 147,006 (84.0%), respectively. As for the diabetic cases, the distributions were skewed and had very heavy tails on the right side, especially in the medication group. The basic statistics were a mean of 30,117, a median of 17,389, and a SD of 58,858 in the medication group; and a mean of 10,160, a median of 2681, and a SD of 33,165 in the non-medication group. In 2.7% and 23.6% of cases, the medical costs were zero. The mean medical cost in the medication group was 3.0 times as much as that in the non-medication group.
3.2. Results of the Power Transformation Tobit Models
3.2.1. Diabetic and Non-Diabetic Groups
Table 1 shows a summary of the explanatory variables in the diabetic and non-diabetic groups. Japan is a racially homogeneous society, we could not evaluate its effect. The mean SBP and DBP (SD in parentheses, mmHg) were 131.6 (18.0) and 79.6 (11.5) in the diabetic group and 125.5 (17.1) and 77.6 (12.2) in the non-diabetic group, respectively. For other variables, the values of Age, BMI, Triglyceride, Blood_sugar, Urine_sugar, GGT, AST, and ALT in the diabetic group were higher than those in the non-diabetic group. On the other hand, the values of the ratio of females, HDL, and LDL were lower in the diabetic group.
Figure 1. Distribution of medical costs (diabetic group).
Figure 2. Distribution of medical costs (non-diabetic group).
Figure 3. Distribution of medical costs (medication group).
Figure 4. Distribution of medical costs (non-medication group).
Table 1. Summary of explanatory variables (diabetic and non-diabetic groups).
SD: Standard Deviation.
Table 2 shows the estimation results of the power transformation tobit model. Since the sample size was quite large, we used 1% as the significance level. For BP variables, estimates of SBP were positive in the diabetic group and negative in the non-diabetic group. Their t-values were 4.089 and −11.049, respectively. This means that the higher SBP significantly increased medical costs in the diabetic group but reduced them in the non-diabetic group. These results do not coincide with the results of ACCORD and SPRINT. The estimates of DBP were negative and positive in the diabetic and non-diabetic groups, respectively, and both of them were significant. It is interesting that the signs of SBP and DBP became the opposites in the diabetic and non-diabetic groups. Other than BP variables, estimates of Age, Height, BMI, Urine_sugar, Urine_protein, and AST were positive and significant; and those of HDL, HDL, Triglyceride Blood_sugar, and Society 3 were negative and significant in the diabetic group. In the non-diabetic group, Age, Female, Height, BMI, Blood_sugar, Urine_sugar, Urine_protein, GGT, ALT, and F_year 15 were positive and significant; and HDL, LDL, AST, Society 2, and Society 3 were negative and significant. LDL and HDL are referred to as “bad” and “good” cholesterol, respectively. LDL (bad) contributes to fatty buildups in the arteries, and HDL (good) removes LDL cholesterol from the arteries [37] [38] . However, as shown in a previous study [24] , higher LDL values lower the medical costs in both groups. Although the signs of AST are opposite in the diabetic and non-diabetic groups, other variables show similar trends in both groups.
3.2.2. Hypertension Medication and Non-Medication Groups
Table 3 shows a summary of the explanatory variables in the hypertension medication and non-medication groups. The means of SBP and DBP were 135.1 mmHg (16.2) and 83.0 (11.0) in the medication group and 123.9 (16.8) and 76.7 (11.9) in the non-medication group, respectively. As for the other variables, the values of Age, BMI, Triglyceride, Blood_sugar, Urine_sugar, GGT, AST, and ALT were higher in the medication group than in the non-medication group. On the other hand, the values of the ratio of females, HDL, and LDL were lower in the non-medication group.
Table 4 shows the estimation results of the power transformation tobit model. For BP variables, estimates of SBP were negative in both the medication and non-medication groups. Their t-values were −3.719 and −22.029 in the two groups, respectively. This means that the higher SBP reduced the medical costs significantly. The estimates of DBP were negative with a t-value of −25.359 in the medication group and positive with a t-value of 7.113 in the non-medication group. As for variables other than the BP variables, estimates of Age, Height, BMI, Urine_sugar, Urine_protein, and AST were positive and significant in the medication group; and estimates of HDL, HDL, Triglyceride Blood_sugar, Society 2, and Society 3 were negative and significant in the medication group. In the non-medication group, the estimates of Age, Female, Height, BMI, Blood_sugar, Urine_sugar, Urine_protein, GGT, ALT, and F_year 15 were positive and significant, and those of HDL, LDL, Society 2, and Society 3 were negative and significant. Most of the variables showed similar trends in both groups.
3.3. Probit Analysis of CVD/HD
In Societies 1 and 2, individuals were asked if they had CVD/HD as anamnesis. (Information on CVD/HD was not available for Society 3.) In our dataset, 3009 or 2.5% cases answered “yes” ( ), 113,685 answered “no” ( ), and the total number of cases was 119,394. These cases were analyzed by the probit model given in Equation (4), and a summary of the explanatory variables is given in Table 5. The results of the probit analysis are given in Table 6. For BP variables, both estimates of SBP and DBP were negative, and neither of them were significant at the 1% level. For non-BP variables, the estimates of AGE, BMI, and Urine_protein were positive and significant and those of Female, HDL, LDL, and Society 2 were negative and significant.
Table 2. Results of estimation (diabetic and non-diabetic groups).
SE: standard error; **: Significant at the 1% level.
Table 3. Summary of explanatory variables (hypertension medication and non-medication groups).
Table 4. Results of estimation (hypertension medication and non-medication groups).
SE: standard error; **: Significant at the 1% level.
Table 5. Summary of explanatory variables.
SD: Standard Deviation.
Table 6. Results of estimation (probit model).
SE: standard error, **: Significant at the 1% level.
4. Discussion
We analyzed the effects of BP on medical costs by dividing the dataset into subgroups based on whether the subjects had diabetes and took hypertension medications. In the diabetic group, a higher SBP made the medical costs higher, and a higher DBP made the medical costs lower. In the non-diabetic group, the effect was the opposite; that is, a higher SBP made the medical costs lower, and a higher DBP made the medical costs higher. The results for SBP were the opposite of those of two important previous studies, the ACCORD and SPRINT studies.
Higher SBP made the medical costs lower in both the hypertension medication and non-medication groups. However, a higher DBP made the medical costs lower in the medication group but higher in the non-medication group. Therefore, at least for SBP, we could deny the possibility that the effects of hypertension medications, which make medical costs higher and BP levels lower, were strong enough to reverse the relationship between SBP and medical costs.
In the probit analysis, the estimate of SBP was negative but insignificant at even the 5% significance level. The estimate of DBP was not significant at the 1% level but was significant at the 5% level. However, the sign was negative, and it did not provide any evidence that high BP made the probability of CVD/HD higher. We could not obtain indisputable evidence of the relationships between BP and medical costs, even when the effects of diabetes and hypertension medications were considered. The influence of the 2017 ACC/AHA guideline is very large; as stated by the members of the ACC/AHA Writing Committee [1] , “The focus is on medical practice in the United States, but guidelines developed in collaboration with other organizations can have a global impact.” Further studies are absolutely necessary to determine the effects of BP on CDV/HD.
For non-BP variables, the estimates of Age, BMI, and Urine_protein were positive; those of HDL, LDL, and Society 2 were negative and significant (at the 1% level) for all five models. BMI represents obesity, and the t-values were 10.988, 51.692, 32.424, 38.179, and 14.212 for the five models. They are significant at any reasonable significance level. Obesity is related to hypertension [39] [40] [41] [42] . Hence the recommendation to reduce obesity through lifestyle improvement is still very important. On the other hand, hypertension medications have various side effects [43] [44] , and their careful usage [45] is strongly suggested.
LDL is often called “bad” cholesterol. However, a higher level of LDL reduced not only the medical costs but also the probability of CVD/HD in all five models, suggesting the necessity to revise the functions and roles of LDL. Urine_protein could be a good indicator of an individual’s health condition.
The estimates for Females were positive and significant for the medical cost equations except in the diabetic group, but negative for the CVD/HD equations. Gender might be an important factor to be considered when establishing a health index for hypertension.
Although the estimates were not significant in the non-diabetic group, triglycerides reduced the medical costs and CVD/HD probabilities in other equations. The estimator of Blood_sugar was negative in the diabetic group and positive in the other estimations. It might be related to symptoms of diabetes. The estimates of Urine_sugar were positive and significant for all medical cost groups. The estimator was also positive in the CVD/HD equation, and Urine_sugar might be another candidate for a health indicator. For GGT, AST, and ALT, the results of the diabetic and medication groups were opposite those of the non-diabetic and non-medication groups in terms of medical costs. None of their estimators were significant in the CVD/HD equation. The estimates of Societies 2 and 3 were negative and significant (expect in the probit analysis, in which the data for Society 3 were not available), and the sizes of health insurance societies may affect the health outcomes.
5. Conclusions
In this study, the effects of BP on medical costs and CVD/HD probabilities were analyzed using the transformation tobit and probit models. We used a dataset containing 175,123 medical checkups and 6,312,125 receipts from 88,211 individuals, which was obtained from three health insurance societies. We first divided the dataset by whether individuals had diabetes and were taking hypertension medications. The medical costs were analyzed by the power transformation tobit model in a total of four groups. For the diabetic and non-diabetic groups, we obtained results for SBP opposite to those of two previous important studies, i.e., ACCORD and SPRINT. In both the medication and non-medication groups, the estimators of SBP were negative and significant, indicating that the higher SBP reduced the medical cost. Next, we evaluated the probability of CVD/HD using probit models. SBP was not significant, and DBP was significant at the 5% level (not at the 1% level), but the estimated values were negative. These results suggested that the 2017 ACC/AHA guideline was not supported at least for SBP, even if the influences of diabetes and hypertension medications were removed.
For non-BP variables, the estimates of Age, BMI and Urine_protein were positive; and those of HDL, LDL, and Society 2 were negative and significant for all five models. BMI represents obesity, and reducing BMI reduced both medical costs and probabilities. Hence the recommendation to reduce obesity through lifestyle improvement is very important. Although LDL is considered “bad” cholesterol, a higher level of LDL reduced not only medical costs but also the probability of CVD/HD in all five models. Thus it might be necessary to revise the functions and role of LDL. Urine_protein could be a good indicator of an individual’s health condition. Although the estimates did not become significant in some models, gender was considered to be an important factor to be considered to establish a health index for hypertension. Urine_sugar was positive and significant in all medical cost groups, and this might be another candidate for a health indicator. The estimates of Societies 2 and 3 were negative and significant, and thus the sizes of health insurance societies might affect health outcomes.
In this paper, we mainly evaluated the effects of BP on medical costs and the probability of CVD/HD. The influence of the 2017 ACC/AHA guideline is so large that further studies to reevaluate the relationships between BP and health conditions should be done as soon as possible. To obtain more precise conclusions, analyses using a larger dataset with a longer time-range from various insurance societies are necessary. Sociodemographic and clinical characteristics of the participants are other important factors. These are subjects to be studied in the future.
Acknowledgements
This study was supported by a Grant-in-Aid for Scientific Research, “Analyses of Medical Checkup Data and Possibility of Controlling Medical Expenses (Grant Number: 17H22509),” from the Japan Society of Science, and by a research grant, “Exploring Inhibition of Medical Expenditure Expansion and Health-oriented Business Management Based on Evidence-based Medicine” from the Research Institute of Economics, Trade and Industry (RIETI). The dataset was used with agreements of the health insurance societies and anonymized at the health insurance societies. This study was approved by the Institutional Review Boards of the University of Tokyo (number: KE17-30). The authors would like to thank the health insurance societies for their sincere cooperation in providing us the data. The data were used with agreements of the insurance societies. We would also like to thank an anonymous referee for his/her helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Nawata, K. and Kimura, M. (2018) Empirical Studies of Effects of High Blood Pressure on Medical Costs and Heart Disease: Is the 2017 ACC/AHA Guideline Supported by Enough Evidence? Health, 10, 1498-1519. https://doi.org/10.4236/health.2018.1011115
References
- 1. Whelton, P.K., Carey, R.M., Arrow, W.S. et al. (Writing Committee Members) (2018) 2017 ACC/AHA/AAPA/ABC/ACPM/AGS/APhA/ASH/ASPC/NMA/PCNA Guideline for the Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Hypertension, 71, e13-e115. (Correction: Hypertension, e140-e144.)
- 2. Whelton, P.K., Carey, R.M., Arrow, W.S., et al. (2018) 2017 Guideline for Blood Pressure in Adults. American College of Cardiology. http://www.acc.org/latest-in-cardiology/ten-points-to-remember/2017/11/09/11/41/2017-guideline-for-high-blood-pressure-in-adults
- 3. Carey, R.M. and Whelton P.K. for the 2017 ACC/AHA Hypertension Guideline Writing Committee (2018) Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults: Synopsis of the 2017 American College of Cardiology/American Heart Association Hypertension Guideline. Annals of Internal Medicine, 168, 351-335. https://doi.org/10.7326/M17-3203
- 4. Chobanian, A.V., Bakris, G.L., Black, H.B., et al. (2003) Seventh Report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure. Hypertension, 42, 1206-1252. https://doi.org/10.1161/01.HYP.0000107251.49515.c2
- 5. National Heart, Lung, and Blood Institute, U.S. Department of Health and Human Services (2004) National High Blood Pressure Education Program: Seventh Report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure (Complete Report). https://www.nhlbi.nih.gov/files/docs/guidelines/jnc7full.pdf
- 6. American Academy of Family Physicians (AAFP) (2017) AAFP Decides to Not Endorse AHA/ACC Hypertension Guideline, Academy Continues to Endorse JNC8 Guideline. AAFP News. https://www.aafp.org/news/health-of-the-public/20171212notendorseaha-accgdlne.html
- 7. Wright, J.T., Williamson, J.D., Whelton, P.K., et al. (SPRINT Research Group) (2015) A Randomized Trial of Intensive versus Standard Blood-Pressure Control. New England Journal of Medicine, 373, 2103-2116. https://doi.org/10.1056/NEJMoa1511939
- 8. Pak, T.R., Rodriguez, M.D. and Roth, F.P. (2015) Why Clinical Trials Are Terminated. bio-Rxiv. https://www.biorxiv.org/content/biorxiv/early/2015/07/02/021543.full.pdf
- 9. Harvard Health Publishing (2017) The Power of the Placebo Effect. Harvard Medical School. https://www.health.harvard.edu/mental-health/the-power-of-the-placebo-effect
- 10. Hoenemeyer, T.W., Kaptchuk, T.J., Mehta, T.S., et al. (2018) Open-Label Placebo Treatment for Cancer-Related Fatigue: A Randomized-Controlled Clinical Trial. Scientific Reports, 8, 2784. https://doi.org/10.1038/s41598-018-20993-y
- 11. The ACCORD Study Group (2010) Effect of Intensive Blood-Pressure Control in Type 2 Diabetes Mellitus. New England Journal of Medicine, 362, 1575-1585. https://doi.org/10.1056/NEJMoa1001286
- 12. Lewington, S., Clarke, R., Qizilbash, N., et al. (2002) Age-Specific Relevance of Usual Blood Pressure to Vascular Mortality: A Meta-Analysis of Individual Data for One Million Adults in 61 Prospective Studies. Lancet, 360, 1903-1913. https://doi.org/10.1016/S0140-6736(02)11911-8
- 13. Nawata, K., Sekizawa, Y. and Kimura, M. (2018) Evaluation of Blood Pressure Control Medicines Using Health and Medical Checkup Data in Japan: Alternative Methods for Randomized Controlled Trials. Health, 10, 587-603. https://doi.org/10.4236/health.2018.105047
- 14. Dickersin, K., Chan, S., Chalmersx, T.C., et al. (1987) Publication Bias and Clinical Trials. Controlled Clinical Trials, 8, 343-353. https://doi.org/10.1016/0197-2456(87)90155-3
- 15. Hopewell, S., Loudon, K., Clarke, M.J., et al. (2009) Publication Bias in Clinical Trials Due to Statistical Significance or Direction of Trial Results, (Review). Cochrane Database of Systematic Reviews, No. 1, MR000006. http://sverigesradio.se/diverse/appdata/isidor/files/83/5775.pdf
- 16. Lexchin, J., Bero, L.A., Djulbegovic, B.B., et al. (2003) Pharmaceutical Industry Sponsorship and Research Outcome and Quality: Systematic Review. BMJ, 326. https://doi.org/10.1136/bmj.326.7400.1167
- 17. Gorman, B.K. and Porter, J.R. (2011) Social Networks and Support, Gender, and Radical/Ethic Disparities in Hypertension among Older Adults. Population Research & Policy Review, 20, 885-911. https://doi.org/10.1007/s11113-011-9215-4
- 18. Ibrahim, M.M. and Damasceno, A. (2012) Hypertension in Developing Countries. The Lancet, 380, 611-619. https://doi.org/10.1016/S0140-6736(12)60861-7
- 19. Omiboni, S., Aristizabal, D., De la Sierra, A., et al. (2016) Hypertension Types Defined by Clinic and Ambulatory Blood Pressure in 14142 Patients Referred to Hypertension Clinics Worldwide. Data from ARTEMIS Study. Journal of Hypertension, 34, 2187-2198. https://doi.org/10.1097/HJH.0000000000001074
- 20. Nawata, K., Matsumoto, A., Kajihara, K., et al. (2017) Evaluation of the Distribution of and Factors Affecting Blood Pressure Using Medical Checkup Data in Japan. Health, 9, 124-137. https://doi.org/10.4236/health.2017.91009
- 21. Rapsomaniki, E., Timmis, A., George, J., et al. (2014) Blood Pressure and Incidence of Twelve Cardiovascular Diseases: Lifetime Risks, Healthy Life-Years Lost, and Age-Specific Associations in 1.25 Million People. The Lancet, 383, 1899-1911. https://doi.org/10.1016/S0140-6736(14)60685-1
- 22. Heckman, J. (1979) Sample Selection Bias as a Specification Error. Econometrica, 47, 153-161. https://doi.org/10.2307/1912352
- 23. Muntner, P., Carey, R.M., Gidding, S., et al. (2018) Potential U.S. Population Impact of the 2017 ACC/AHA High Blood Pressure Guideline. Journal of the American College of Cardiology, 71, 109-118. https://doi.org/10.1016/j.jacc.2017.10.073
- 24. Nawata, K. and Kimura, M. (2018) Does High Systolic Blood Pressure Truly Increase Medical Expenditure? An Empirical Analysis of the New 2017 ACC/AHA Hypertension Guideline. Health, 10, 1044-1065. https://doi.org/10.4236/health.2018.108079
- 25. American Diabetes Association (ADA) (2014) Diagnosis and Classification of Diabetes Mellitus. Diabetes Care, 37, S81-S90. https://doi.org/10.2337/dc14-S081
- 26. ADA (2015) Diabetes Basic. http://www.diabetes.org/
- 27. International Diabetes Federation (2018) What Is Diabetes. https://www.idf.org/aboutdiabetes/what-is-diabetes.html
- 28. NCD Risk Factor Collaboration (2016) Worldwide Trends in Diabetes since 1980: A Pooled Analysis of 751 Population-Based Studies with 4•4 Million Participants. The Lancet, 387, 1513-1530. https://doi.org/10.1016/S0140-6736(16)00618-8
- 29. Diaz-Valencia, P.A., Bougneres, P. and Valleron, A.J. (2015) Global Epidemiology of Type 1 Diabetes in Young Adults and Adults: A Systematic Review. BMC Public Health, 15, 255. https://doi.org/10.1186/s12889-015-1591-y
- 30. National Health Service (NHS) (2016) Treatment—High Blood Pressure (Hypertension). https://www.nhs.uk/conditions/high-blood-pressure-hypertension/treatment/
- 31. American Heart Association (AHA) (2017) Types of Blood Pressure Medications. http://www.heart.org/en/health-topics/high-blood-pressure/changes-you-can-make-to-manage-high-blood-pressure/types-of-blood-pressure-medications
- 32. Healthdirect (2017) Blood Pressure Medication. Department of Health. https://www.healthdirect.gov.au/blood-pressure-medication
- 33. Healthline Editorial Team (2018) A List of Blood Pressure Medications. https://www.healthline.com/health/high-blood-pressure-hypertension-medication
- 34. Nawata, K. and Kimura, M. (2017) Evaluation of Medical Costs of Kidney Diseases and Risk Factors in Japan. Health, 9, 1734-1749. https://doi.org/10.4236/health.2017.913127
- 35. Japanese Law Translation (2009) Industrial Safety and Health Act. http://www.japaneselawtranslation.go.jp/law/detail/?id=1926&vm=&re
- 36. Nawata, K., Niita, A., Watanabe, S., et al. (2006) An Analysis of the Length of Stay and the Effectiveness of Treatment for Hip Fractured Patients in Japan: Evaluation of the Revision of the 2002 Medical Service Fee Schedule. Journal of Health Economics, 25, 722-739. https://doi.org/10.1016/j.jhealeco.2005.11.002
- 37. Centers Disease Control and Prevention (2017) LDL and HDL Cholesterol: “Bad” and “Good” Cholesterol. https://www.cdc.gov/cholesterol/ldl_hdl.htm
- 38. AHA (2017) HDL (Good), LDL (Bad) Cholesterol and Triglycerides. http://www.heart.org/HEARTORG/Conditions/Cholesterol/HDLLDLTriglycerides/HDL-Good-LDL-Bad-Cholesterol-and-Triglycerides_UCM_305561_Article.jsp#.WxUKUkjRCUk
- 39. Kennel, W.B., Brand, N., Skinner, J.J., et al. (1967) The Relation of Adiposity to Blood Pressure and Development of Hypertension: The Framingham Study. Annals of Internal Medicine, 67, 48-59. https://doi.org/10.7326/0003-4819-67-1-48
- 40. Kotchen, T.A. (2010) Obesity-Related Hypertension: Epidemiology, Pathophysiology, and Clinical Management. American Journal of Hypertension, 23, 1170-1178. https://doi.org/10.1038/ajh.2010.172
- 41. Jiang, S.-Z., Lu, W., Zong, X.-F., et al. (2016) Obesity and Hypertension. Experimental and Therapeutic Medicine, 12, 2395-2399. https://doi.org/10.3892/etm.2016.3667
- 42. Loggi, M., Lombardi, M. and Caldarone, E. (2017) The Relationship between Obesity and Hypertension: A Comprehensive Overview on Twins. Hypertension Research, 40, 947-963. https://doi.org/10.1038/hr.2017.75
- 43. MedlinePlus (2018) High Blood Pressure Medicines. U.S. National Library of Medicine. https://medlineplus.gov/ency/article/007484.htm
- 44. WebMed (2018) Side Effects of High Blood Pressure Medications. https://www.webmd.com/hypertension-high-blood-pressure/guide/side-effects-high-blood-pressure-medications#1
- 45. Harvard Heath Publishing (2017) Controlling Blood Pressure with Fewer Side Effects. Harvard Medical School. https://www.health.harvard.edu/heart-health/controlling-blood-pressure-with-fewer-side-effects
Appendix: Sample Selection Biases
Here, we considered the problem of sample selection biases. To the best of our knowledge, this is the first explicit representation of medical data analyses. Suppose that an individual goes to a hospital or clinic and participates in a survey if
, (5)
where is a latent variable that represents a health condition, and are vectors of explanatory variables (including BP levels) and parameters. Let where 1(A) is an indicator function that takes 1 if A is true and 0 otherwise.
An individual becomes CVD/HD if
. (6)
is another latent variable, and let . and are other vectors of explanatory variables and parameters. follows a two-variate normal distribution with a mean of zero. For the general public, the probability of developing CVD/HD is given by
. (7)
is the distribution function of the standard normal distribution.
By the property of the multivariate normal distribution, we can write
(8)
without loss of generality. and are independent and follow a standard normal distribution. The probability that the patient participates in the survey and develops CVD/HD is given by
(9)
where is the expected value with respect to , and is the density function of the standard normal distribution.
Here, by partial integration, we get
(10)
Now,
(11)
, , .
Therefore,
(12)
Then we get
.