Engineering
Vol.07 No.11(2015), Article ID:61614,24 pages
10.4236/eng.2015.711067
Trilinear Hexahedra with Integral-Averaged Volumes for Nearly Incompressible Nonlinear Deformation
Craig D. Foster*, Talisa Mohammad Nejad
University of Illinois at Chicago, Civil and Materials Engineering, Chicago, IL, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 24 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
Many materials such as biological tissues, polymers, and metals in plasticity can undergo large deformations with very little change in volume. Low-order finite elements are also preferred for certain applications, but are well known to behave poorly for such nearly incompressible materials. Of the several methods to relieve this volumetric locking, the
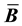 method remains popular as no extra variables or nodes need to be added, making the implementation relatively straightforward and efficient. In the large deformation regime, the incompressibility is often treated by using a reduced order or averaged value of the volumetric part of the deformation gradient, and hence this technique is often termed an
method remains popular as no extra variables or nodes need to be added, making the implementation relatively straightforward and efficient. In the large deformation regime, the incompressibility is often treated by using a reduced order or averaged value of the volumetric part of the deformation gradient, and hence this technique is often termed an
 approach. However, there is little in the literature detailing the relationship between the choice of
approach. However, there is little in the literature detailing the relationship between the choice of
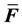 and the resulting
and the resulting
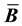 and stiffness matrices. In this article, we develop a framework for relating the choice of
and stiffness matrices. In this article, we develop a framework for relating the choice of
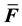 to the resulting
to the resulting
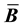 and stiffness matrices. We examine two volume-averaged choices for
and stiffness matrices. We examine two volume-averaged choices for , one in the reference and one in the current configuration. Volume-averaged
, one in the reference and one in the current configuration. Volume-averaged
 formulation has the advantage that no integration points are added. Therefore, there is a modest savings in memory and no integration point quantities needed to be interpolated between different sets of points. Numerical results show that the two formulations developed give similar results to existing methods.
formulation has the advantage that no integration points are added. Therefore, there is a modest savings in memory and no integration point quantities needed to be interpolated between different sets of points. Numerical results show that the two formulations developed give similar results to existing methods.
Keywords:
Incompressibility, Volumetric Locking, Strain Projection, B-Bar, F-Bar, Finite Element

1. Introduction
Many materials exhibit nearly incompressible responses over some part of their deformation. Biological tissues, rubbers, metals undergoing plastic deformation, and soils under undrained conditions are examples. To model these materials in a finite element (FE) context, care has to be taken to use elements designed for nearly incompressible behavior. The fact that low-order finite elements perform poorly for nearly incompressible media is well known, and treatment for this issue has received significant attention. There are several ways to view the problem, but one is that standard elements have too many incompressibility constraints which overwhelm the shear response. While higher-order elements can relieve this, even they do not behave optimally. And for certain classes of problems, such as some dynamic problems or problems involving jumps in the displacement field, low-order elements are generally preferred.
Many solutions have been proposed to relieve this volumetric locking effect in low-order elements, particularly quadrilaterals and hexahedra. Reduced integration [1] can reduce the number of volumetric constraints, but results in spurious non-zero energy modes are often called hourglass modes. However, modification can control these modes ( [2] - [5] , among others). Mixed methods treat the mean stress as a separate variable. While effective, the extra set of equations complicates the process and results in higher computation time (see [6] - [9] among others). It should be noted that many times the extra variable may be condensed at the element level, minimizing this extra cost. Assumed enhanced strain formulations add extra terms to the strain and can relieve locking, for example in [10] [11] . Variational multiscale methods [12] - [14] , and other stabilization techniques ( [15] among others) have also been employed to relieve locking, but also add extra complexity to the system.
Because they can be implemented relatively simply in a displacement-only framework, the so-called
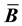 methods have been highly popular. Discussed in [16] for linear elements, these elements replace the volumetric part of the strain-displacement matrix with a reduced-order integration or averaged value. The reduced interpolation order of the volumetric term reduces the number of constraints, relieving the locking. No extra degrees of freedom are added to the system, though in some cases additional integration points are added. While these elements do not formally satisfy the Ladyzenskaya-Babuska-Brezzi stability conditions [17] [18] , they perform well in practice and their relative ease of implementation has made the approach popular.
methods have been highly popular. Discussed in [16] for linear elements, these elements replace the volumetric part of the strain-displacement matrix with a reduced-order integration or averaged value. The reduced interpolation order of the volumetric term reduces the number of constraints, relieving the locking. No extra degrees of freedom are added to the system, though in some cases additional integration points are added. While these elements do not formally satisfy the Ladyzenskaya-Babuska-Brezzi stability conditions [17] [18] , they perform well in practice and their relative ease of implementation has made the approach popular.
For the finite deformation case, these methods have been extended using a so-called
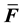 approach. This approach takes a reduced order or average evaluation of the deformation gradient
approach. This approach takes a reduced order or average evaluation of the deformation gradient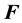 . Several variations on this idea have been proposed, including reduced integration scheme for the logarithm of the volumetric deformation [19] , reduced integration scheme for the volumetric deformation [20] [21] , and an average over the element reference volume of the Jacobian [22] . In another approach, modified Jacobian
. Several variations on this idea have been proposed, including reduced integration scheme for the logarithm of the volumetric deformation [19] , reduced integration scheme for the volumetric deformation [20] [21] , and an average over the element reference volume of the Jacobian [22] . In another approach, modified Jacobian
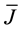 is defined by relating it to a volume change parameter [23] . Most authors choose to use the
is defined by relating it to a volume change parameter [23] . Most authors choose to use the
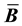 modification for the gradient of the weighting function (virtual velocity gradient), though some do not [20] [21] . While it has not been emphasized in the literature, each choice of
modification for the gradient of the weighting function (virtual velocity gradient), though some do not [20] [21] . While it has not been emphasized in the literature, each choice of
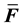 yields a corresponding
yields a corresponding
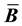 matrix, which in general has a different averaging scheme than the
matrix, which in general has a different averaging scheme than the
In this paper, we develop an 8-node hexahedral element that averages the Jacobian over the element. While the integration procedure adds some modest complexity to the computation time to the code, it avoids tracking variables at an extra integration point. Extra integration points can add memory costs. They can also add significant complexity in multiphysics problems or history-dependent materials, though we do not investigate those here. We examine integral averages in both the reference and current configurations, and detail the relationship between the choice of
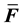
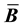
While beyond the scope of this paper, it bears mentioning that the


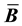
The remainder of the paper is organized as follows: Section 2 discusses integral averages for
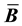
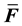
Notation
A few notes on notation: We employ the summation convention in this paper, that a repeated index within a single term of an expression has an implied sum over the range of the index. For example
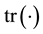
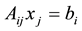
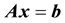
Outer products are represented with the ‘
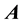
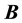
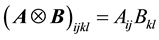
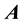
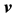
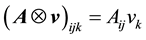
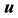
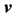

First- and second-order tensors are denoted in bold, e.g.



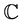
We use curly braces for second-order tensors converted to vectors in Voigt notation. Kinematic quantities have doubled off-diagonal terms unless stated otherwise, while other quantities do not. For example

Similarly, fourth-order tensors converted to Voigt-form matrices are denoted with brackets, e.g.
2.
The basis of the

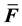


Here,
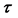
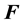

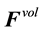
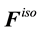
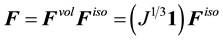
where



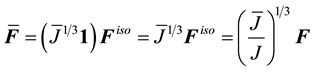
Many forms for
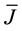

An alternative approach is to use an averaging scheme or stabilization procedure. We adopt the former in the paper. Specifically, we examine two possibilities
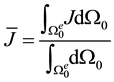
and

The first is a volume average of the Jacobian over the reference volume of the element

Note: As discussed in [19] , for very nearly or completely incompressible materials, hourglass modes may appear due to ill-conditioning of the stiffness matrix. These modes can be alleviated by replacing





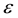
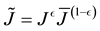
3. Consistent
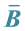
The appropriate function for the
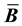

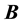
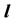

where



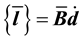
First, we must derive an expression for the modified velocity gradient


The expression for

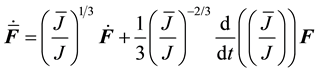
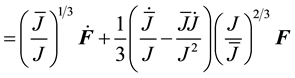
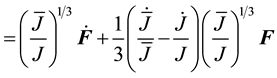
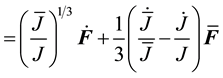
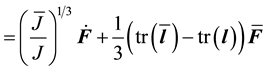
Here we define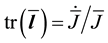


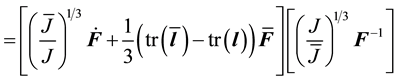
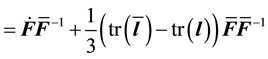
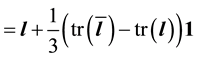
Note that this has the familiar form of the small strain

For the choice of
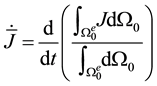
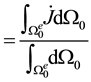
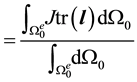
Hence
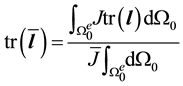
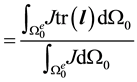
Curiously, averaging J over the reference configuration results in

Averaging J over the current configuration results in a somewhat more complicated formulation. In this case
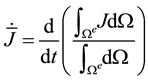

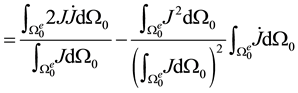
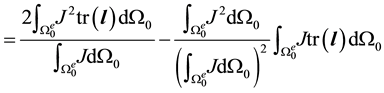
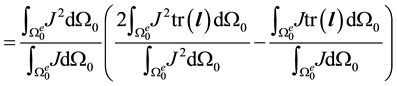

Hence

In a finite element context, we can factor out the element nodal velocity vector implicit in the equations from the finite element shape functions. Recall that
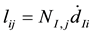

where
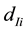
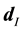
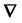
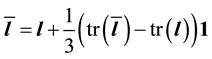


Here,
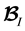
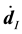

In other words, it is the tensor equivalent of the standard updated Lagrangian

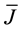
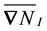

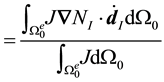
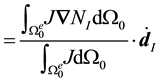

where
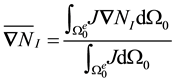
Similarly, for the Jacobian averaged in the current configuration
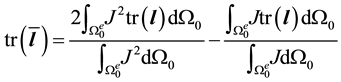
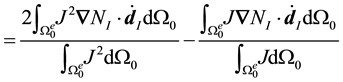
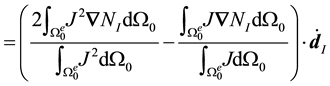
Therefore
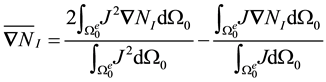
With the correct expression for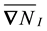

In implementation, this expression is generally rearranged into a vector form such that
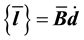
In this case, the nodal submatrix
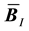
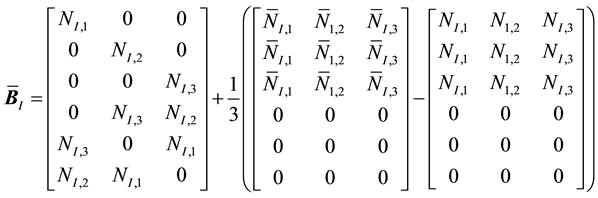
The full

where
We assume that the gradient of the weighting function, or virtual velocity vector, takes the same modifications as that used in the physical velocity gradient. Hence the element internal force vector may be written

This derivation may also be carried out in a total Lagrangian setting, however, the volumetric part does not separate out as cleanly and the formula is more complicated.
Note: It is not strictly necessary to use the same averaging for the virtual velocity gradient as for the actual, or, in fact, any averaging. The authors in [20] use the standard
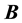
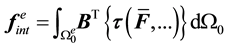
The resulting formulation is somewhat simpler, but is also nonsymmetric. As the authors point out in that article, some materials have a nonsymmetric tangent stiffness already, and for these materials little is lost. However, for materials with a symmetric tangent stiffness, the proposed formulation creates a symmetric stiffness matrix, which has advantages in storage and solution time.
4. Stiffness Matrix
The stiffness matrix may be derived by taking a directional derivative, or another pseudo-time derivative. The derivation is relegated to the appendix, where the latter approach is taken. If
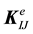
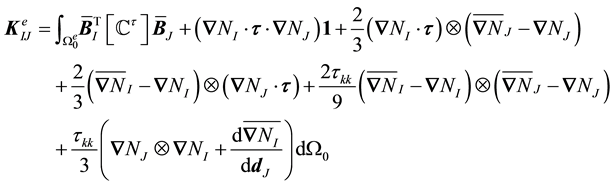
where

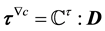
The formula is general, and can be applied for any choice of
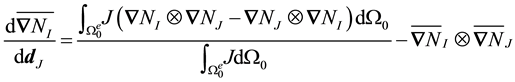
For the Jacobian averaged in the current configuration
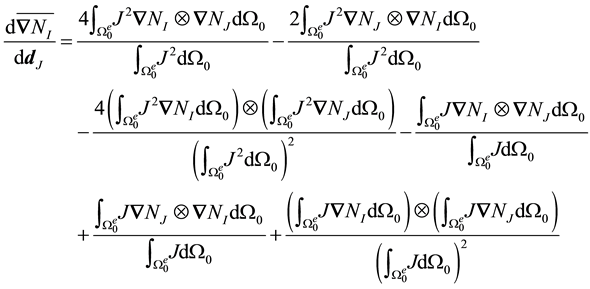
Clearly the second formula is more complex than the first. These formulas are derived in the appendix.
5. Numerical Examples
In this section, the performance of the proposed

5.1. Three-Dimensional Block
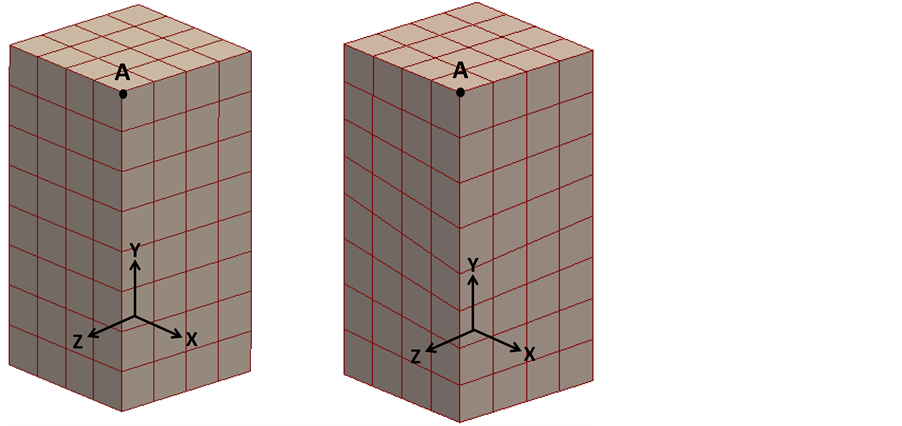
In the first three numerical examples, a nearly incompressible nonlinear elastic block fixed on bottom and subjected to three different loading conditions are presented. The block is 2 meters high with a square cross section of 1 meter, shown in Figure 1. The quantity we compare is the displacement at node A located at (1, 2, 1) meters.
For this set of examples, the material model used is a Neo-Hookean model that follows the decomposition of strain energy function into isochoric and volumetric components:
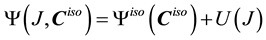
in which U is the penalty function enforcing incompressibility defined as
Figure 1. Geometry of a block with 2 m height and a square cross section of 1 square meter. The block is meshed with 128 regular hexahedra (i.e. cubes) on the left and 128 irregular hexahedra on the right. We focus on comparing the displacement at node A using standard and
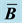
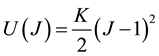
where K is a generalization of the linear bulk modulus. The isochoric part may be defined as

In which


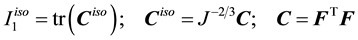
The material parameters of
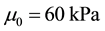
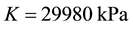
This set of examples investigates the performance of three-dimensional mean dilatation 8-node
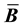
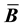
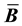
5.1.1. Block Subjected to Side Pressure
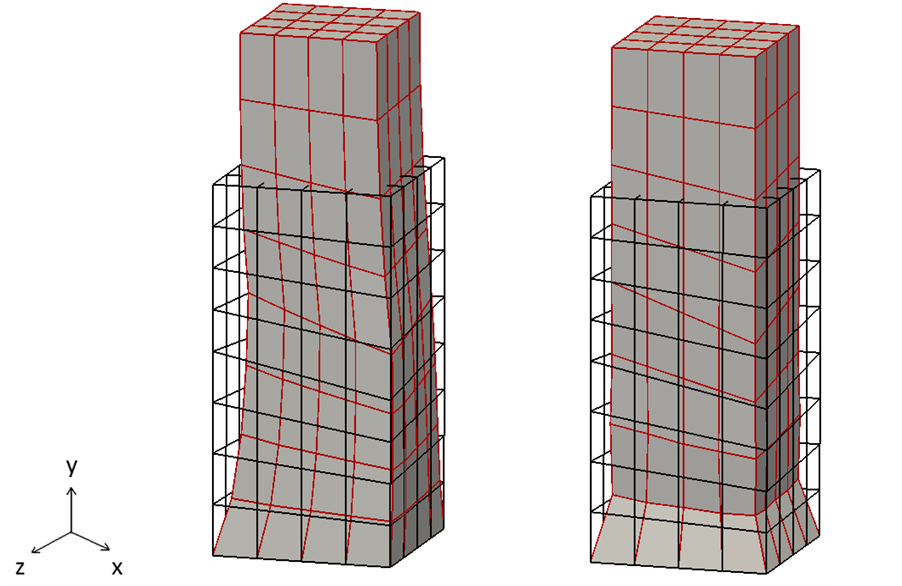
This example is used to assess performance of near incompressible limit material subjected to a side pressure. Follower forces are used. In this block, displacement is fully constrained in bottom and a side pressure of 2 kPa is uniformly applied to the front left edge. Three meshes respectively consisting of 2, 16 and 128 elements are considered to investigate the convergence. For each mesh, the solution for the two element shapes is obtained to ensure that elements with nonconstant initial element Jacobians perform well (for clarity, the element Jacobian is the volume ratio between the physical volume and the volume in the bi-unit cube in the parent domain, and is different from the Jacobian of the deformation which we have been discussing throughout this paper). For each mesh, regular and irregular hexahedra, and each refinement, four cases are run: standard displacement elements with no special treatment of the volumetric deformation,


From the obtained results we can see that average volume
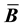

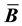
Table 2 illustrates the evolution of the norm of the residual over the iterations for the last loading step for
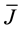
Figure 2. Deformed shape of an incompressible block subjected to side pressure and fixed bottom displacement obtained from FE simulation using (a) standard 8-node hexahedral elements (b) mean- dilatational 8-node
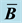

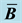
Table 1. Displacement results, in m, obtained at node A, using standard and
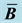
Table 2. Evolution of the residual norm during the last time step in Newton-Raphson iterations with the proposed
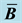
5.1.2. Block Subjected to Compressive Pressure
This example is presented to assess performance of the proposed

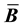
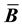
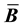
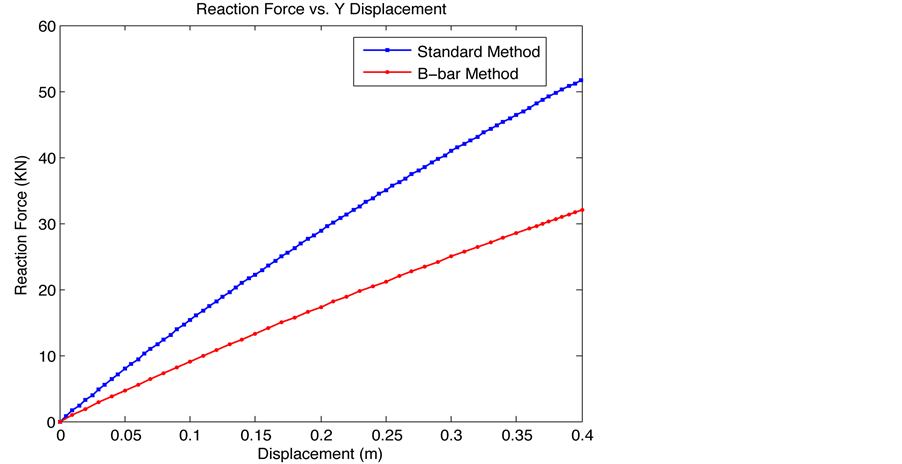
As illustrated in this figure and the table, displacement results are larger with



5.1.3. Block Subjected to Tensile Displacement
In this example, performance of the proposed


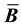
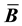
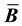
5.2. Cook’s Membrane
Cook’s membrane is a classical plane strain problem used to test performance of elements in nearly incompressible problems under moderate distortion. Here we apply the problem in three dimensions, with one layer of elements in depth and all nodes constrained out of plane. We follow the nonlinear example in [29] , using the Neo-Hoo-kean potential in the previous examples, which is identical to the one is used in that paper.
The geometry is shown in Figure 8, and an upward load of 1 N is distributed evenly across the right hand side. Again following [29] , we use
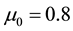
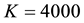
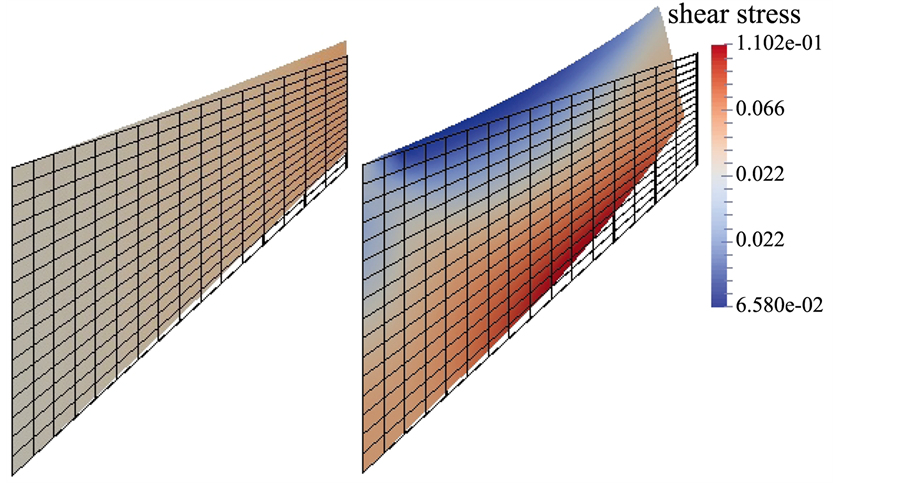
We compare meshes of 16, 64, and 256 elements. The deformed meshes for the standard and

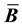
For quantitative comparison, the vertical displacements at the upper right node are recorded. For verification, ANSYS is again run with the Solid 185 element. The results are shown in Table 4. The results between the ANSYS solution and our

Figure 3. Deformed shape of an incompressible block subjected to uniform pressure on top and fixed displacement on bottom obtained from FE simulation using standard 8-node hexahedral elements (on the left) and mean-dilatational 8-node

Figure 4. Deformed shape of an incompressible block subjected to uniform tensile displacement on top and fully restricted displacement on bottom, obtained from FE simulation using standard 8-node hexahedral elements (on the left) and mean-dilatational 8-node
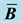
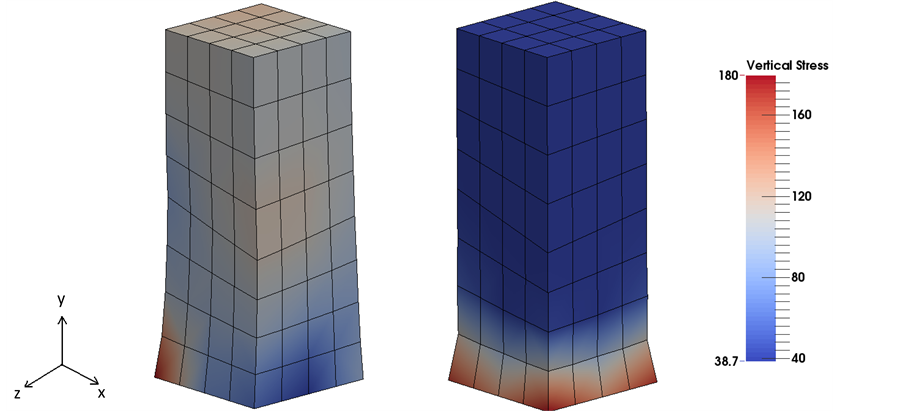
Figure 5. Distribution of Kirchhoff vertical stress τyy obtained from FE simulation using standard 8-node hexahedral elements (on the left) and mean-dilatational 8-node
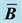
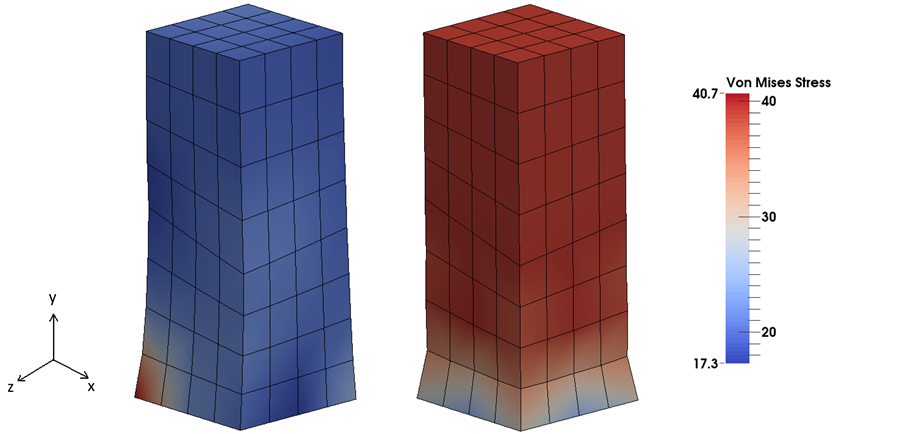
Figure 6. Distribution of Kirchhoff von Mises stress obtained from FE simulation using standard 8-node hexahedral elements (on the left) and mean-dilatational 8-node
Table 3. Displacement results for the block in compression obtained at node A using standard and

Figure 7. Plot of the reaction force versus displacement using standard and

Figure 8. Geometry for Cook’s membrane problem. The model is one mm out of plane, with no deformation allowed in the out-of-plane direction.
Table 4. Vertical displacement results, in mm, at top right node, using standard and

Figure 9. Deformed shapes for both standard integration (left) and

5.3. Incompressible Mouse Cornea Subjected to Pressure
In the final example, the incompressible behavior of a three-dimensional mouse cornea subjected to pressure loading is studied by means of standard and

The mouse cornea is a nearly incompressible soft biological tissue consisting of five layers of which the stroma is the thickest and stiffest. For simplicity, only the stiffness of the stroma is considered in the constitutive model development. The stroma is composed of oriented and dispersed collagen fibrils embedded in nearly incompressible matrix. The material model used is an anisotropic hyperelastic model adapted from Pandolfi and Holzapfel [32] for the human cornea. The model follows the decomposition of the strain energy function into an isochoric component and volumetric components of oriented fibrils distributed in Neo-Hookean matrix:
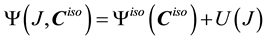
in which U is the penalty function enforcing incompressibility constraints of the cornea defined as
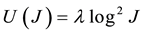
where

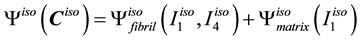
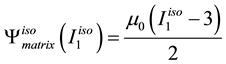
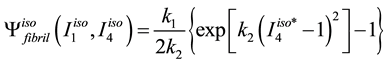


for a given unit orientation vector
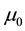
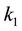
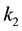
The unit vector
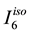

cumferential orientation around the cornea edge. Again, in the transition region, a linear interpolation of the two directions is assumed.
Spheres with different radii of curvature for outer and inner surfaces of the cornea result in varying thickness throughout. For the mouse cornea model, a thickness of 0.3 mm at the apex and 0.1 mm at the edge was assumed. An initial cornea height of 0.84 mm and the distance from cornea center to the inner and outer edges of respectively 1.33 mm and 1.39 mm were used.
The finite element simulation is performed using the standard 8-node hexahedral elements and the proposed

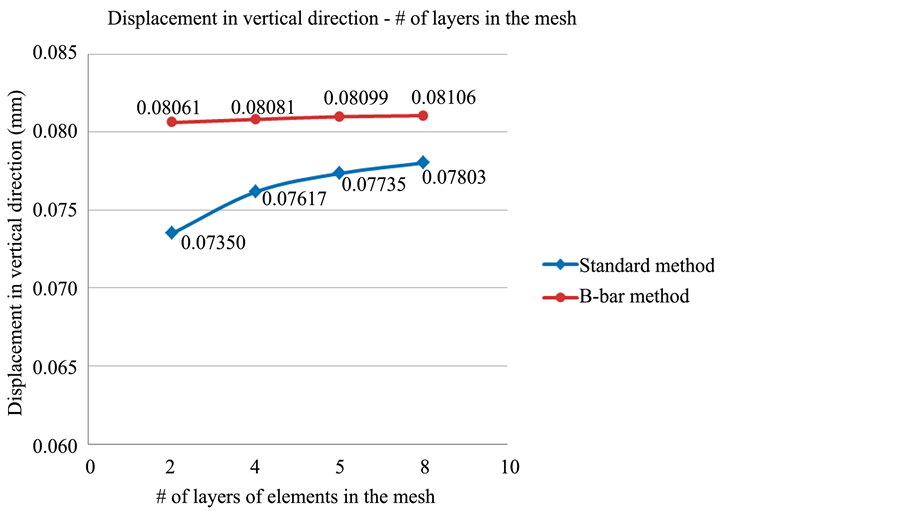
The results of vertical displacement at the apex versus the number of element layers through corneal thickness are shown in Figure 10. The results obtained with standard 8-node hexahedral elements and with 8-node


Figure 10. Vertical Displacement at the cornea apex versus number of layers of elements through the corneal thickness with standard and

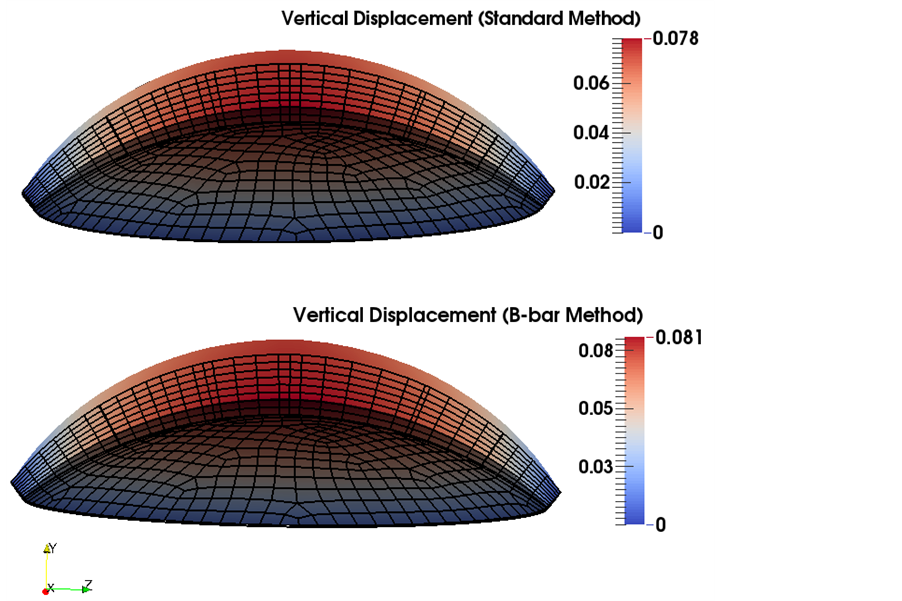
fewer layers, and the standard elements appear to exhibit some locking. Figure 11 also illustrates the deformed shape of the cornea using the standard and

6. Conclusions
In summary, we have developed a
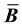

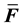


We have examined two possible choices for the integral averaging of the Jacobian, over the reference configuration and over the current configuration. While there may be some justifications for the current configuration as more natural, the formulation is more complex. Since the volume change in nearly incompressible materials
Table 5. Material constants assumed for anisotropic and nonlinear FE simulation of mouse cornea.
Figure 11. Vertical displacement mapping of a mouse cornea subjected to pressure obtained from standard and
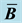
is small, one does not expect there to be a great difference in the results. This observation is confirmed by numerical examples.
Since the formulation is general, it can be applied to other choices of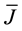
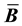
Acknowledgements
The authors gratefully acknowledge the support of the U.S. National Institutes of Health grant 1R21EY020946- 01.
Cite this paper
Craig D.Foster,Talisa MohammadNejad, (2015) Trilinear Hexahedra with Integral-Averaged Volumes for Nearly Incompressible Nonlinear Deformation. Engineering,07,765-788. doi: 10.4236/eng.2015.711067
References
- 1. Hughes, T.J.R. (1987) The Finite Element Method. Prentice-Hall, Upper Saddle River.
- 2. Flanagan, D.P. and Belytschko, T. (1981) A Uniform Strain Hexahedron and Quadrilateral with Orthogonal Hourglass Control. International Journal for Numerical Methods in Engineering, 17, 679-706.
http://dx.doi.org/10.1002/nme.1620170504 - 3. Belytschko, T., Ong, J.S.J., Liu, W.K. and Kennedy, J.M. (1984) Hourglass Control in Linear and Nonlinear Problems. Computer Methods in Applied Mechanics and Engineering, 43, 251-276.
http://dx.doi.org/10.1016/0045-7825(84)90067-7 - 4. Reese, S., Kussner, M. and Reddy, B.D. (1999) A New Stabilization Technique for Finite Elements in Non-Linear Elasticity. International Journal for Numerical Methods in Engineering, 44, 1617-1652.
http://dx.doi.org/10.1002/(SICI)1097-0207(19990420)44:11<1617::AID-NME557>3.0.CO;2-X - 5. Reese, S., Wriggers, P. and Reddy, B.D. (2000) A New Locking-Free Brick Element Technique for Large Deformation Problems in Elasticity. Computers & Structures, 75, 291-304.
http://dx.doi.org/10.1016/S0045-7949(99)00137-6 - 6. Sussman, T. and Bathe, K.J. (1987) A Finite Element Formulation for Nonlinear Incompressible Elastic and Inelastic Analysis. Computers & Structures, 26, 357-409.
http://dx.doi.org/10.1016/0045-7949(87)90265-3 - 7. Chapelle, D. and Bathe, K.J. (1993) The Inf-Sup Test. Computers & Structures, 47, 537-545.
http://dx.doi.org/10.1016/0045-7949(93)90340-J - 8. Kasper, E.P. and Taylor, R.L. (2000) A Mixed-Enhanced Strain Method Part I: Geometrically Linear Problems. Computers & Structures, 75, 237-250.
http://dx.doi.org/10.1016/S0045-7949(99)00134-0 - 9. Kasper, E.P. and Taylor, R.L. (2000) A Mixed-Enhanced Strain Method Part II: Geometrically Nonlinear Problems. Computers & Structures, 75, 251-260.
http://dx.doi.org/10.1016/S0045-7949(99)00135-2 - 10. Simo, J.C., Taylor, R.L. and Pister, K.S. (1985) Variational and Projection Methods for the Volume Constraint in Finite Deformation Elasto-Plasticity. Computer Methods in Applied Mechanics and Engineering, 51, 177-208.
http://dx.doi.org/10.1016/0045-7825(85)90033-7 - 11. Simo, J.C. and Rifai, M.S. (1990) A Class of Mixed Assumed Strain Methods and the Method of Incompatible Modes. International Journal for Numerical Methods in Engineering, 29, 1595-1638.
http://dx.doi.org/10.1002/nme.1620290802 - 12. Masud, A. and Xia, K.M. (2005) A Stabilized Mixed Finite Element Method for Nearly Incompressible Elasticity. Journal of Applied Mechanics-Transactions of the ASME, 72, 711-720.
http://dx.doi.org/10.1115/1.1985433 - 13. Masud, A. and Xia, K.M. (2006) A Variational Multiscale Method for Inelasticity: Application to Superelasticity in Shape Memory Alloys. Computer Methods in Applied Mechanics and Engineering, 195, 4512-4531.
http://dx.doi.org/10.1016/j.cma.2005.09.014 - 14. Xia, K.M. and Masud, A. (2009) A Stabilized Finite Element Formulation for Finite Deformation Elastoplasticity in Geomechanics. Computers and Geotechnics, 36, 396-405.
http://dx.doi.org/10.1016/j.compgeo.2008.05.001 - 15. Ramesh, B. and Maniatty, A.M. (2005) Stabilized Finite Element Formulation for Elastic-Plastic Finite Deformations. Computer Methods in Applied Mechanics and Engineering, 194, 775-800.
http://dx.doi.org/10.1016/j.cma.2004.06.025 - 16. Hughes, T.J.R. (1980) Generalization of Selective Integration Procedures to Anisotropic and Nonlinear Media. International Journal for Numerical Methods in Engineering, 15, 1413-1418.
http://dx.doi.org/10.1002/nme.1620150914 - 17. Brezzi, F. and Fortin, M. (1991) Mixed and Hybrid Finite Element Methods. Springer, Berlin, Heidelerg and New York.
http://dx.doi.org/10.1007/978-1-4612-3172-1 - 18. Szabo, B. and Babuska, I. (1991) Finite Element Analysis. Wiley, New York.
- 19. Moran, B., Ortiz, M. and Shih, C.F. (1990) Formulation of Implicit Finite-Element Methods for Multiplicative Finite Deformation Plasticity. International Journal for Numerical Methods in Engineering, 29, 483-514.
http://dx.doi.org/10.1002/nme.1620290304 - 20. de Souza Neto, E.A., Peric, D., Dutko, M. and Owen, D.R.J. (1996) Design of Simple Low Order Finite Elements for Large Strain Analysis of Nearly Incompressible Solids. International Journal of Solids and Structures, 33, 3277-3296.
http://dx.doi.org/10.1016/0020-7683(95)00259-6 - 21. de Souza Neto, E.A., Peric, D. and Owen, D.R.J. (2008) Computational Methods for Plasticity. Wiley, New York.
http://dx.doi.org/10.1002/9780470694626 - 22. Nagtegaal, J.C., Parks, D.M. and Rice, J.R. (1974) On Numerically Accurate Finite Element Solutions in the Fully Plastic Range. Computer Methods in Applied Mechanics and Engineering, 4, 153-177.
http://dx.doi.org/10.1016/0045-7825(74)90032-2 - 23. Mathisen, K.M., Okstad, K.M., Kvamsdal, T. and Raknes, S.B. (2011) Isogeometric Analysis of Finite Deformation Nearly Incompressible Solids. Journal of Structural Mechanics, 44, 260-278.
- 24. de Souza Neto, E.A., Pires, F.M.A. and Owen, D.R.J. (2005) F-Bar-Based Linear Triangles and Tetrahedral for Finite Strain Analysis of Nearly Incompressible Solids. Part I: Formulation and Benchmarking. International Journal for Numerical Methods in Engineering, 62, 353-383.
http://dx.doi.org/10.1002/nme.1187 - 25. Elguedj, T., Bazilevs, Y., Calo, V.M. and Hughes, T.J.R. (2008) F-Bar Projection Method for Finite Deformation Elasticity and Plasticity Using NURBS Based Isogeometric Analysis. International Journal of Material Forming, 1, 1091- 1094.
http://dx.doi.org/10.1007/s12289-008-0209-7 - 26. Belytschko, T., Tsay, C.S. and Liu, W.K. (1981) A Stabilization Matrix for the Bilinear Mindlin Plate Element. Computer Methods in Applied Mechanics and Engineering, 29, 313-327.
http://dx.doi.org/10.1016/0045-7825(81)90048-7 - 27. Doll, S., Schweizerhof, K., Hauptmann, R. and Freischläger, C. (2000) On Volumetric Locking of Low-Order Solid and Solid-Shell Elements for Finite Elastoviscoplastic Deformations and Selective Reduced Integration. Engineering Computations, 17, 874-902.
http://dx.doi.org/10.1108/02644400010355871 - 28. Belytschko, T., Liu, W.K. and Moran, B. (2000) Nonlinear Finite Elements for Continua and Structures. John Wiley & Sons, New York.
- 29. Brink, U. and Stein, E. (1996) On Some Mixed Finite Element Methods for Incompressible and Nearly Incompressible Finite Elasticity. Computational Mechanics, 19, 105-119.
http://dx.doi.org/10.1007/BF02824849 - 30. Rhee, J., Nejad, T.M., Comets, O., Flannery, S., Gulsoy, E.B., Iannaccone, P. and Foster, C. (2015) Promoting Convergence: The Phi Spiral in Abduction of Mouse Corneal Behaviors. Complexity, 20, 22-38.
http://dx.doi.org/10.1002/cplx.21562 - 31. Nejad, T.M., Iannaccone, S., Rutherford, W., Iannaccone, P.M. and Foster, C.D. (2015) Mechanics and Spiral Formation in the Rat Cornea. Biomechanics and Modeling in Mechanobiology, 14, 107-122.
http://dx.doi.org/10.1007/s10237-014-0592-6 - 32. Pandolfi, A. and Holzapfel, G.A. (2008) Three-Dimensional Modeling and Computational Analysis of the Human Cornea Considering Distributed Collagen Fibril Orientations. Journal of Biomechanical Engineering-Transactions of the ASME, 130, Article ID: 061006.
http://dx.doi.org/10.1115/1.2982251 - 33. Sheppard, J., Hayes, S., Boote, C., Votruba, M. and Meek, K.M. (2010) Changes in Corneal Collagen Architecture during Mouse Postnatal Development. Investigative Ophthalmology & Visual Science, 51, 2936-2942.
http://dx.doi.org/10.1167/iovs.09-4612
Appendix 1: Stiffness Derivation
As mentioned previously, the stiffness matrix may be derived using a directional derivative or a pseudo-time derivative. Here, we take the latter approach. We examine the nodal subvector of the element internal force vector

where, as mentioned previously,
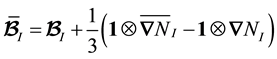



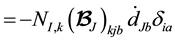


For convenience, for the remainder of the derivation, we will move the nodal subscript of the

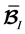


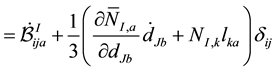
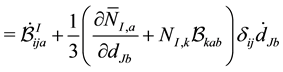
The time derivative of the nodal subvector of the element internal force vector, then, can be written

Examining the quantity inside the integral

We examine the second term first. Recall that
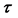


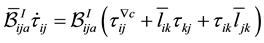
rather than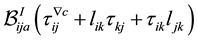

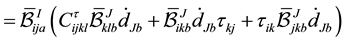
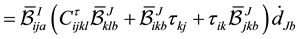
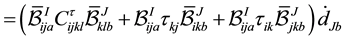

Taking the second and third quantities one at a time
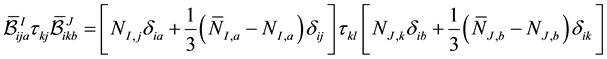

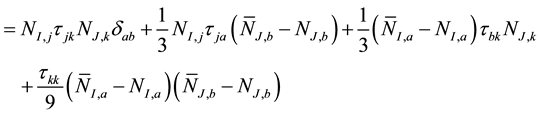

The third quantity becomes

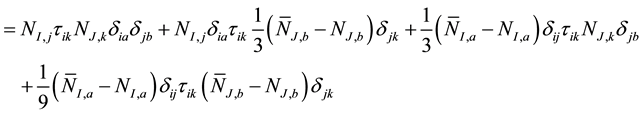


Next we evaluate
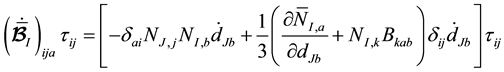
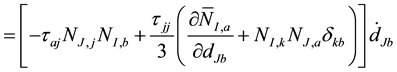


Adding up all these quantities, we find that

and hence the nodal submatrices of the element stiffness matrix may be written
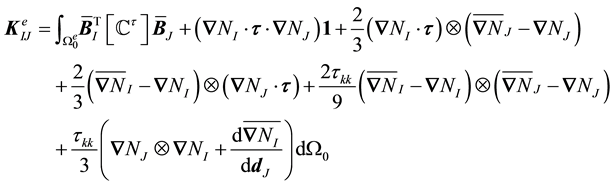
The first term is the common “material stiffness” with the modified

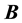

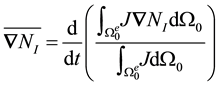
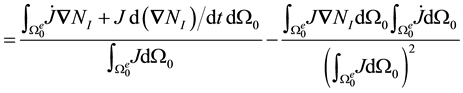
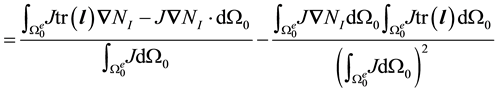
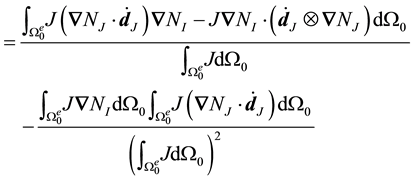
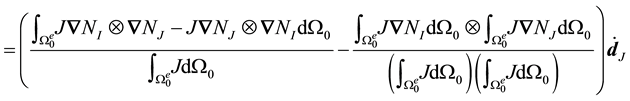
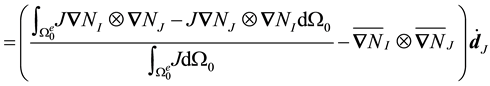
Therefore,
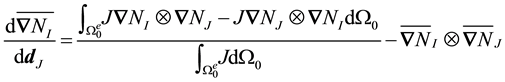
The process for the Jacobian averaged in the current configuration is the same, though the calculations are more tedious.
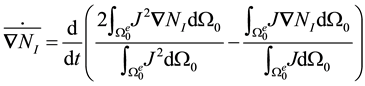
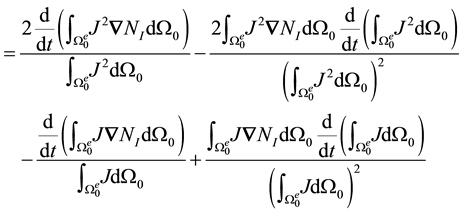
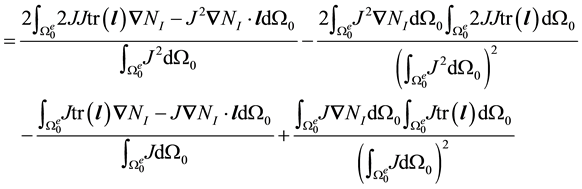
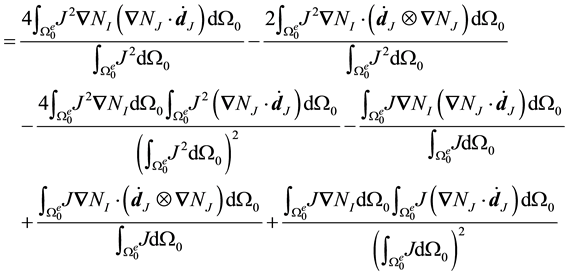

Hence, the derivative we seek must be

NOTES
*Corresponding author.