Engineering
Vol.07 No.01(2015), Article ID:53425,9 pages
10.4236/eng.2015.71004
Similarity and Comparison of the Electrodynamics Characteristics of Switched Reluctance Motors SRM with Those of Series DC Motors
Abdelmajid Berdai1*, Abdelaziz Belfqih1, Jamal Boukherouaa1, Faissal El Mariami1, Abdelhamid Hmidat1, Vladimir Vlasenko2, Valery Titjuk2
1TCSI Laboratory, ESE Research Group, Department of Electrical Engineering National School of Electricity and Mechanics (ENSEM), University Hassan II Ain Chock, Casablanca, Morocco
2Department of Electromechanics, Krivoy Rog National University, Krivoy Rog, Ukraine
Email: *a.berdai@gmail.com, a-belfqih@hotmail.com, j.boukherouaa@yahoo.fr, vlasenko_v@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2014; accepted 14 January 2015; published 21 January 2015
ABSTRACT
The switched reluctance motor is appreciated in variable speed drives through his simplicity of design, his low cost, his high reliability and high ability to regulate which allow him to compete with the other common types of electric drives. The mathematical modelling of switched reluctance motors (SRM) allows his study in the areas of research and conception. In this paper, we present the developing of a methodology using the combined model of switched reluctance motor drive bases in standard equations of electrical machines with the field theory analysis of magnetic circuit. Then, the elaboration of mathematical models for switching reluctance motor (SRM) proposes his application based on a similarity with series DC motor to simplify the conception of control of electrical drives systems [1] with Closed Loop Control.
Keywords:
Switched Reluctance Motor, Similarity, Equivalent Parameters

1. Introduction
SRMs have made a place for themselves among other electric actuators due to their low production cost and major robustness, both of which make them an interesting alternative for a number of industrial applications. Nonetheless, the SRM is a highly non-linear actuator (pronounced saturation of the magnetic circuit).
In order to analyse or control a SRM, a model must be available, which is why researchers had to come up with an electromagnetic model of a SRM. No accurate analytic model as yet exists for a SRM. The best electromagnetic model is one that most closely approaches all of the SRM’s electromagnetic fields. The model must be extremely close to measurement data while being simple enough to be used for control purposes. A very simple model necessitating little calculation risks modelling the system’s characteristics inaccurately, while a very accurate model requires burdensome calculations. A model that is both simple and accurate has therefore to be found in order to be able to study the SRM’s behaviour.
Mathematical modelling of switched reluctance motors (SRMs) [2] [3] is still the main way of enabling their study in the fields of scientific research and design.
Creation of methods for calculation and optimisation of SRM motors’ electromechanical characteristics is one of the focuses in electromechanical engineering that has seen active development over recent years. The bibli- ography on the problem includes a considerable number of scientific articles and works that may be grouped into three main categories:
・ Methods based on the electric circuits concept.
・ Methods based on the magnetic fields theory.
・ Combined methods.
This article proposes the combined method, bringing together the simplicity of electric circuit methods and the accuracy and polyvalence of electromagnetic field methods, which are regarded as the most perspective methods. In the case of switched reluctance motors, the combined method model enables static calculation of the electromagnetic field with use of other results obtained in the form of differential equations describing the dynamics of the electrical drive system. We will then go on to create mathematical models of the switched reluc- tance motor (SRM), proposing its application on the basis of similarities with the model for the series DC motor, in order to simplify the design of control systems for closed-loop electrical drives.
2. Theoretical Approach and Synthesis
As with all types of electric machines, an SRM’s control system is composed of equations of electrical balance for each of the electric machine’s stator phases, and equations for rotor movement.
The electrical relationship of the SRM stator coil’s balance position is defined as follows:
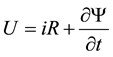 (1)
(1)
where 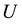 is the supply voltage.
is the supply voltage.
Generally speaking, the magnetic flow through coil 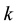 in an electric machine with several coils is equal to:
in an electric machine with several coils is equal to:
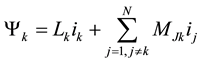 (2)
(2)
with:
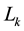 : Inductance specific to a
: Inductance specific to a 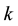 phase;
phase;
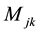 : Mutual inductance between phases
: Mutual inductance between phases 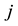 and
and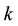 .
.
As, with symmetrical control in full step, currents overlap slightly depending on time, the equation’s second term (2) may be ignored for a certain relationship between the motor’s load and the number of stator coils. In this case, a coil’s magnetic flow may be entirely determined by its own inductance.
As the inductance of an SRM coil depends on rotor angle in relation to the latter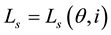 , Equation (1) may be written as follows:
, Equation (1) may be written as follows:
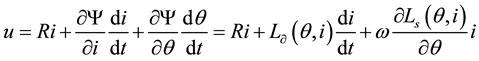 (3)
(3)
or
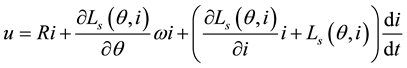 (4)
(4)
where
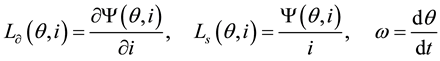 (5)
(5)
Respectively designating dynamic inductance, static inductance and angular rotor speed.
The influence of dynamic inductance will be the subject of a separate analysis and will not be taken into con- sideration in this article.
The electrical relationship of the voltage at an SRM phase’s terminals in balance position may therefore be expressed as follows:
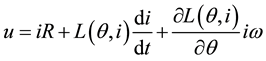 (6)
(6)
Relationship (6) in its structure is identical to the relationship of a series DC motor’s armature voltage [4] .
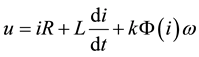 (7)
(7)
For the series motor, the first magnetisation curve shows that excitation flow is dependent on armature vol- tage. In the linear part of the curve, assuming an unsaturated magnetic circuit (before the saturation knee point), we can nonetheless write that 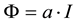 (with
(with
The main difference between SRM equations and those for DC motors lies in the influence of phase induc- tance, the excitation flow defining the CEMF and the electromagnetic torque on the rotor’s angular position.
Consequently, it is of interest to set up the nature and parameters of the influence of phase inductance on the rotor’s angular position.
3. Mathematical Model of the SRM’s Magnetic System
Basic parameters for the SRM’s equivalent schema depend on the electric machine’s structure and geometry as well as on the magnetic characteristics of the materials used to construct it. These days, digital methods are applied, utilised to create simulations of the electromagnetic field.
Simulation of the magnetic field is regarded as one of the most complex and valuable methods currently used in analysis of electric machines. To respond to the question, the magnetic fields theory method has been applied increasingly over recent years as it has a number of significant advantages over other methods, including major reduction in duration and volume of the preparatory work required for determination of the magnetic circuit’s parameters; virtual absence of limits to magnetic systems’ physical and geometrical properties; easy determi- nation of the characteristics of the magnetic system’s (MS) design and of the specific properties of magnetic materials, and consequently, more accurate analysis of the magnetic field’s distribution; and simplicity in calcu- lating the equivalent schema’s parameters and determining the machine’s characteristics (phases’ own and shared inductances, electromagnetic torque, speed, etc.) [5] .
The finite element method (FEM) is the method most often used in digital calculation of electric machines’ magnetic fields. There is a wide range of software making use of the method, including Maxwell, ELCUT, JUMP, LOMAN, FEMM and Femlab. Given that the method requires discretisation not only of the magnetic environment but of the whole space, in accordance with well-defined meshing, it is clear that creation of a more complex meshing is required, especially for the electric machine’s air gap during modelling of its magnetic field, which means considerably greater complexity and volume of calculations.
The boundary integral equation (BIE) method is often applied to resolution of field problems [6] . We have used it in [7] depending on the magnetic induction vector, which is conserved as a secondary dipole of the magnetic field. The method’s main advantages are that it restricts calculation zones to the magnetic circuit and the relative simplicity it provides in determining a number of important factors in the magnetic system’s makeup, including its non-linear anisotropy, vector hysteresis and magnetic viscosity.
The essential goal of the proposed method is determination of the distribution of magnetisation vector 



For a two-dimensional space [5] :

with:







For a linear, isotropic milieu (unsaturated magnetic system), the integral equation depending on magnetic induction vector 

where 

To solve two-dimensional equations, it is helpful to use the complex form of Equation (11) [8] :

where the symbol “

and as this was indicated in [6] , the following relationship is verified:

where


This last equation may easily be generalised in the event of a non-linear, non-homogenous anisotropic milieu, even with the effect of hysteresis.
We may now introduce the new vector 

Integral Equation (16) depending on the “non-classical” variable magnetic field in [7] [8] is a modified magneto static equation whose main advantages are limitation of the zones of secondary dipoles and its exact characterisation of universal magnetic properties. Therefore, in non-linear cases, the tensor’s differential form is:

Which shows that, even in the rectangular function 




To continue on to characterisation of

After calculation of the magnetic induction at whatever point in the space defined by the expression:

The generalised complex potential takes the form:

where 

4. Analysis of the SRM’s Magnetic Circuit
The combined approach’s main problem results from the need for simultaneous calculation of the variation of the magnetic field’s characteristics and those of the corresponding electrical circuits. Solving the problem in such a context greatly complicates the simulation process.
Use of the dynamic characteristics method is regarded as one of the possibilities for achievement of the com- bined method enabling design of the circuit of the field mathematical model of SRM [9] . The essentials of this method, in the case of its application for SRM simulation, consist of establishing a connection between the stator coil’s inductance and the rotor’s angle of rotation
As the simulation subject, we have used an SRM with the following performances and characteristics:
Magnetic circuit material: 3405-quality steel; Magnetic circuit prototype: 8/6 (classic configuration); Stator exterior diameter: 62 mm; Stator interior diameter: 32.5 mm; Length of active steel: 36 mm; Stator base thick- ness: 5.8 mm; Stator height: 9 mm; Rotor tooth height: 4.5 mm; Air gap: 0.25 mm; Polar angle of stator: 18˚; Angle of rotor grooves: 19˚; Shaft diameter: 9 mm; Number of spires per phase: 80; Nominal power: 1.5 kW; Nominal rotation frequency: 1500 rev/minute; Power supply voltage: 480V; Nominal current of stator: 12.4 A; Active coil resistance: 3 ohms.
On the basis of results obtained in studying the magnetic circuit, we were able to define the characteristic of the stators’ inductance depending on the angle of the rotor
In real-life conditions, inductance coil stator also depends on the value of current 
Variation of phase inductance depending on the rotor’s angle of rotation may be approximated by the simple expression (20)―(Figure 1).

It is makes it easier if we operate with coherent values for inductance 


As calculation of the field shows, the value of inductance 



Inductance 

Figure 1. Phase inductance depending on angle θ for a stator current series.
Figure 2. Variation of phase inductance depending on angle θ.
where


Therefore, Equation (20) takes the form:

Graphing of 
5. Analysis of the Consistency of the Mathematical Model of the SRM
In order to solve this system of equations and analyse the consistency of results obtained, we created a pro- gramme using Lazarus, which is a multiplatform IDE (integrated development environment) developed in Ob- ject Pascal. To solve differential equations, we used the Runge-Kutta 4th order method (RK4) with a constant in- tegration speed of
Figure 4 shows the variation of the rotor’s angular speed and angle of rotation at switched operating speed. Comparing Figure 4(a) and Figure 4(b), we may observe that the rotor’s angular balance position depends on the resistive torque opposed by the load of inductive character. The motor only stops when the motor torque is lower than the resistive torque.
Figure 5(a) shows an SRM’s phase currents at start-up. As Figure 5(b) shows, we have determined the op- erational curves of SRM operating speed―i.e., the process of motor start-up and establishment of its on-load operation.
On the basis of the graphs in Figure 4 and Figure 5, obtained from the results of calculations carried out by the SRM’s mathematical model, and considering the quality of the models’ concordance and convergence to- wards the basic principle of electromechanical engineering, we may conclude that the mathematical model de- veloped is a consistent one.
Figure 3. Approximate function of the

Figure 4. SRM switched operating speed. (a) Мs = 7 N∙M; (b) Мs = 21 N∙M.

Figure 5. Graphs of SRM operating speeds defined by the mathematical model. (a) Phase current at beginning of start-up. (b) SRM start-up and running on-load.
6. Comparison of the Electrodynamics Characteristics of SRMs with Those of Series DC Motors
By using Fourier series decomposition of function

Comparing Equations (6) and (10), it can clearly be seen that, in the case of series motors, coefficient “k” is a constant value (within the limits of the linear zone of the first magnetisation curve), while for an SRM, the same coefficient depends on the rotor’s angular position.
Applying the same principle, with the aim of simplifying the SRM’s model, we have replaced the variable 

The SRM may be controlled by varying the supply voltage as well as by varying the value of the supply volt- age’s commutation angles 


With 




Therefore, the average calculated at the end of an operating interval in a similar phase is equal to 
The value of the current’s angle of extinction 

By using the relationship of the previously obtained function 

where


In the same way, it is necessary to define the average value of the supply voltage applied to a phase:

Knowing the law of voltage variation at a phase’s terminals, we may write:

Therefore, in order to determine the parameters of a series motor equivalent to an SRM, it is necessary to carry out the following actions and calculations:
1) On the basis of calculation of the magnetic field, define the data tabulation of function
2) Present the relationship of the function obtained in the form of a decomposition in Fourier series and dis- tinguish the decomposition’s significant terms;
3) For the defined values of commutation angles 

4) Calculate the SRM’s operating speeds using the mathematical model suggested;
5) Calculate the series motor’s operating speeds and assess the convergence of results obtained.
Figure 7 presents graphs of comparative curves of speed―a) and start-up current; b) for on-load operation of the SRM (thin line) and equivalent series motor (thick line).
The relative error for the models considered is around 4% - 5%.
This error is caused by a measure of inaccuracy in determining the equivalent series motor’s coefficient of proportionality Y. Figure 8 shows that accurate calculation of the coefficient could result in greater concordance of the graphs of currents and angular speeds.
The methodology proposed for determining parameters for the equivalent of a DC series motor for various engineering applications provides a sufficient degree of concordance between the dynamic characteristics of an SRM and a DC series motor.
Figure 6.

Figure 7. Comparison of SRM and equivalent series motor operating speeds.

Figure 8. SRM Operating speeds in the closed-loop cascade regulation control system with setup of critical optimum.
7. Use of Results Obtained for Analysis and Synthesis of Cascade Regulation of SRM Control Systems
With the help of known expression (28), current and speed regulator coefficients may be calculated. Taking account of technical optimum conditions, the current regulator’s transfer function equals:

where




The current transfer function:

where


In order to check the stability of the synthetized system’s control and determine the control’s quality indica- tors, we carry out mathematical modelling of the SRM in the closed-loop regulation system [14] .
For resolution of this control system and analysis of the consistency of results obtained, a programme was developed in Object Pascal with the help of the Lazarus IDE. To solve differential equations, we used the Runge- Kutta 4th order method with a constant integration speed of
Figure 8(а) presents the diagrams of the SRM’s current and angular speed during start-up. Figure 3(b) pre- sents the diagrams of current and angular speed during application of a load to the SRM.
8. Conclusions
Based on analysis of the SRM’s magnetic system field method and analysis of the mathematical model of the SRM, we have established electrodynamic similitude between the SRM and the DC motor. A method for deter- mining the DC motor equivalent’s parameters has been determined. Taking the classical approach to synthesis of the automatic regulation system, calculation of the current and speed regulators for adjusting the SRM’s coordi- nates has been carried out.
Using the mathematical modelling method, it has been shown that the closed-loop synthesized cascade regu- lation system is stable and possesses satisfactory indicators of control quality.
References
- Kuznetsov, V.A. and Kuzmichev, V. (2003) Switched Reluctance Motor. Editions МЭИ, Moscow, 70.
- Lawrenson, P.J., Stephensem, J.M., Blekinsop, P.T., Corda, J. and Fulton, N.N. (1980) Variable Switched Reluctance Motor. Proc. Inst. Eng, 127, 253-265.
- Praveen, V. (2001) Design of Switched Reluctance Motors and Development of a Universal Controller for Switched Reluctance and Permanent Magnet Brushless DC Motor Drives. Dissertation Submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in Electrical Engineering, Blacksburg, 203.
- Vaskovsky, J.M. (2007) Field Analysis of Electric Machines. T. Handbook, KIEV: NTU “KPI”, 192.
- Chornij, A., Lugovoj, A., Rodkin, D., Sisjuk, G. and Kremenchuk, S.O. (2001) Modeling of Electromechanical Systems. Kremenchuk Mykhailo Ostrohradskyi National University, Kremenchuk, 376.
- Tozoni, O.V. and Mayergoyz, I.D. (1974) Calculationof Three-Dimensional Electromagnetic Fields. Kiev: Tehnіcs, 352.
- Nascimento, J.M.L., Rolim, L.G.B., Heidrich, P., Suemitsu, W.I. and Hanitsch, R. (1995) Design and Simulation Results of a Switched Reluctance Motor. Proceeding of Third Brazilian Power Electronics, 79-83.
- Tolmachev, S.T. (1983) Special Methods for Solving Magnetostatic Problems. Kiev: High School, 166.
- Miller, T.J.E. (1993) Switched Reluctance Motor and Their Control. Magna Physics and Clarendon Press, Oxford.
- Suriano, J.R. (1992) Design Methodology for Low Speed Variable Reluctance Motors. School of Electrical Engineering, Purdue University, West Lafayette, 90 p.
- Ramu, K. (2001) Switched Reluctance Motor Drives: Modeling, Simulation, Analysis, Design, and Applications. Boca Raton London New York Washington DC, 416 p.
- Soares, F. and Costa Branco, P.J. (2001) Simulation of a 6/4 Switched Reluctance Motor Based on Matlab/Simulink Environment. IEEE Transactions on Aerospace and Electronic Systems, 37, 989-1099. http://www.researchgate.net/publication/3003381_Simulation_of_a_64_switched_reluctance_motor_based_onMatlabSimulink_environment http://dx.doi.org/10.1109/7.953252
- Vukosavic, S. and Stephanovic, V.R. (1990) SRM Inverter Topologies: A Comparative Evaluation. IEEE Industry Applications Society, 946-958. http://vukosavic.etf.bg.ac.rs/papext.pdf
- Elliot, C.R., Stephenson, J.M. and McClelland, M.L. (1995) Advances in Switched Reluctance Drive System Dynamic Simulation. Proceedings of EPE ’95, 3, 622-626.
NOTES
*Corresponding author.










