Engineering
Vol.06 No.13(2014), Article ID:52145,27 pages
10.4236/eng.2014.613082
Finite Element Modelling of Steel Beams with Web Openings
Flavio Rodrigues1, Pedro C. G. da S. Vellasco2, Luciano R. O. de Lima2*, Sebastião A. L. de Andrade2
1PGECIV―Post Graduate Program in Civil Engineering, UERJ―State University of Rio de Janeiro, Rio de Janeiro, Brazil
2Structural Engineering Department, UERJ―State University of Rio de Janeiro, Rio de Janeiro, Brazil
Email: rodriguesflavio@oi.com.br, vellasco@uerj.br, *lucianolima@uerj.br, seb.andrade@uol.com.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; revised 7 November 2014; accepted 22 November 2014
ABSTRACT
Height limitations are not uncommon in multi-storey buildings due to economic requirements and esthetical considerations. Substantial spaces are normally required to enable the passage of large pipes and ducts beneath steel beams leading to uneconomic floor heights. The most adopted solu- tion for this issue is the use of steel beam web openings to provide the required space for services. These openings could lead to a significant decrease of the beam load carrying capacity depending on the adopted openings shape, size and location. These aspects motivated the present study based on FE simulations calibrated against numerical and test results. The results accuracy en- abled a comprehensive parametric analysis of beams with web openings to be made focused on the profile size, web opening location, among others. The study also investigated the efficiency of longitudinal stiffeners welded at the opening region and benefits of using an adequate edge con- cordance radius in beams with rectangular and square openings. The obtained results showed the need of using welded longitudinal stiffeners in order to increase the beams ultimate load carrying capacity. This adoption can double or even triple the ultimate load of beams with rectangular and square opening heights equal to 0.75 H, respectively.
Keywords:
Non-Linear Analysis, Steel Structures, Web Openings, Steel Design and Behavior, Finite Element Method

1. Introduction
Height limitations are not uncommon in multi-storey buildings due to economic requirements and esthetical considerations. Substantial spaces are normally required to enable the passage of large pipes and ducts beneath steel beams leading to uneconomic floor heights. Various solutions can be used to overcome these problems, i.e.: tapered and haunched beams or stub girders and composite trusses but the most adopted solution is the use of steel beam web openings to provide the required space for services.
Various authors and standards, Chung and Ko [1] , Chung and Lawson [2] , Lawson [3] , Darwin [4] , Redwood and Cho [5] , Oehlers and Bradford [6] have indicated that two approaches (Tee Section and Perforated Section) are possible for the design of steel and composite beams with web openings. An interesting procedure, based on plastic section analysis methods, is reported by Chung et al. [7] to design these girders. Other numerical and experimental investigations on the design recommendations for steel and composite beams with web openings [8] are available in the literature but led to specific rules or empirical formulae for general design [9] .
Chung et al. [10] for steel beams and Chung and Lawson [2] for composite beams stated that services that re- quires web openings up to 75% of the beam height are not uncommon (Figure 1). These openings could lead to a significant decrease of the beam load carrying capacity depending on the adopted openings shape, size and lo- cation. Circular and rectangular opening are frequently used with a possible adoption of stiffeners welded near the web openings to improve the beam load carrying capacity.
Lakusic et al. [11] developed a study about the buckling curve for lateral-torsional buckling resistance of cas- tellated beams considering an experimental and a numerical analysis based on finite elements models. Accord- ing to the obtained results, the use of the buckling curved for welded beams [12] -[14] , category in which castel- lated beams are included, instead of the buckling curve c for rolled sections, leads to a severe value for the reli- ability index target i.e. 3.8 associated to the structure class RC2. Radic et al. [15] performed a numerical analy- sis of castellated beams considering two different procedures for the calculation of the elastic critical moment for lateral torsional buckling comparing FE results and Eurocode 3 procedures [12] - [14] . The research results show that the web opening of the castellated beams has little influence on the value of the elastic critical mo- ment for the lateral-torsional buckling. Other works can be cited concerning the web openings beams behaviour. Basher et al. [16] investigated the effects of circular or square web openings on the ultimate strength of horizon- tally curved composite plate girders. Hagen et al. [17] and Hagen and Larsen [18] performed some numerical simulations in order to provide data for the development of a design model for the shear capacity of steel girders with web openings, with and without transverse stiffeners and opening reinforcements. Lagaros et al. [19] studied an optimum design of 3D steel structures having perforated I-section beams. Lian and Shanmugan [20] reported that on plate girders curved in plan containing centrally placed circular web openings, the ob- served failure mechanism in the tests was similar to that observed in plate girders without web openings,
Figure 1. Beam with a series of circular openings [2] .
the only difference being the position of plastic hinges on the flange plates. Liu and Chung [21] presented a comprehensive finite element investigation on steel beams with web openings of various shapes and sizes is re- ported in this paper. And finally, Wang and Chung [9] developed a finite element modelling of perforated com- posite beams with flexible shear connectors.
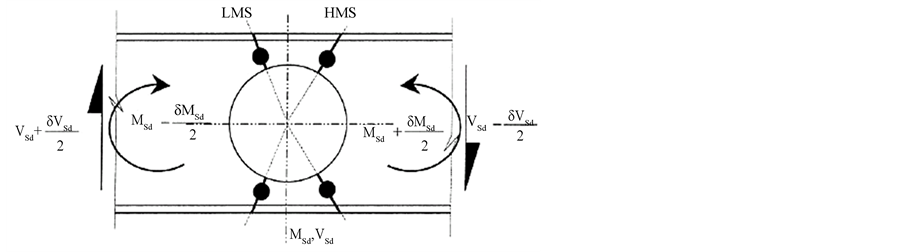
Steel beams with web openings are frequently governed by Vierendeel collapse mechanism that occurs due to a change rate in the bending moment distribution (and consequently, the shear force) along the opening [22] . This bending moment increase is usually resisted by upper and lower “Tees” through their respective local bending strengths, Figure 2 [22] . The “Tees” local bending resistance can be improved by using horizontal stif- feners welded above and below the web openings. This is even more relevant for the cases where fatigue is a controlling factor.
The Vierendeel collapse mode frequently interacts with other ultimate limit states associated to the beam structural design inhibiting the development of simple design rules to evaluate the influence of the openings over the member resistance. This motivated the present study that used finite elements simulations to evaluate the structural behaviour of steel beams with web openings. The opening height usually controls the bending and shear collapses at the perforated sections. On the other hand, the opening width controls the Vierendeel collapse mechanism that also depends on the local shear and bending resistances of the upper and lower “Tees”. Figure 2 depicts the three local actions induced at the upper and lower “Tees” present in a perforated section subjected to global bending moment (Mo,Sd) and a shear force (Vo,Sd). These actions are: the axial force, NT, due to the global bending moment (Mo,Sd), the shear force, VT, due to the global shear force (Vo,Sd), and the bending moment MT, that appears due to the shear force (Vo,Sd) transmitted along the opening length.
The presence of web opening in steel beams introduces three different failure modes, i.e., shear, bending and Vierendeel collapses. The Vierendeel collapse, depicted in Figure 3, occurs due to the formation of four plastic hinges on the “Tees” generated by the lateral shear force transmitted along the web opening.
Generally the shear and bending moment capacities of the perforated sections can be easily evaluated. How- ever, the “Tees” bending resistance is difficult to be determined due to the simultaneous presence of axial, shear forces induced by the global bending stresses acting at the perforated section. Additionally, the correct assess- ment of the collapse mechanism is directly related to four plastic hinge formations and requires the use of plastic design concepts.
Usually an increase of the web opening height reduces the beam shear and bending capacities. Alternatively,
Figure 2. Perforated section force distribution [22] .
Figure 3. Vierendeel mechanism along a circular web opening [10] .
an increase on the web opening length do not significantly affect the beam shear and bending capacities but in- creases the local Vierendeel bending moment acting on the “Tees”, reducing the perforated section Vierendeel collapse capacity.
These aspects motivated the present study based on FE simulations calibrated against numerical and test re- sults. The results accuracy enabled a comprehensive parametric analysis of beams with web openings to be made focused on the profile size, web opening location, among others. This paper also investigated the effi- ciency of longitudinal stiffeners welded at the opening region and benefits of using an adequate edge concor- dance radius in beams with rectangular and square openings.
2. Analytical Model
An analytical model proposed by Darwin [4] to predict the structural behaviour of beams with web openings was used to serve as an additional tool to evaluate and compare the results of the present investigation. In the above mentioned reference [4] , the author presents a moment-shear interaction curve to take into account the simultaneous effects of bending and shear.
The simultaneous actions of bending and shear forces occur at various locations over the beam span. At a web opening, the two forces interact to produce lower resistance values than the obtained under pure bending or pure shear. The interaction curve used to consider bending ϕMn and shear resistance ϕVn design is given by Equation (1):
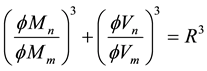 (1)
(1)
where Mn is the actual bending moment present at beam centre span, Vn is the actual shear force present at beam centre span, Mm is the bending moment resistance, Vm is the shear force resistance and R is the ratio between the factored load to the section design capacity at an opening.
The factored loads in the web opening were checked using the interaction curve given by Equation (1). If the value R is equal to or less than the unity, the design is satisfactory. In order to evaluate directly the beam ultimate resistance presented in this paper, all the load and resistance factors design were considered equal to 1.0.
3. Numerical Model
Finite element models were developed to simulate the structural behaviour of steel beams with web openings [23] . These models were calibrated against numerical investigation made by Chung et al. [10] and by experi- mental results performed by Redwood and Mccutcheon [24] .
Physical and geometrical non-linearities were incorporated in the finite element model aiming to simulate the collapse phenomena as accurately as possible. A Newton Raphson algorithm was considered in these analyses to obtain the nonlinear solution.
The numerical models adopted shell finite elements (SHELL181) depicted in Figure 4, present in the ANSYS finite element program [25] . This element presents four nodes with six DOF per node, i.e., translations and rota- tions on the X, Y, and Z axis, respectively.
Figure 4. Shell element―Ansys library [25] .
The loads and supports present in the experimental steel beams were simulated by using restrictions on ap- propriated nodes in the numerical model. A finite element mesh sensitivity analysis was first performed to en- sure that it was properly refined to adequately represent the investigated phenomenon [23] . This study enables the determination of a mesh with the minimum possible element number to accurately represent the steel beam with web opening experiments.
The model material non-linearity was considered through a bilinear elastoplastic response with a 5% strain hardening and a 205,000 MPa Young’s modulus. The rupture and yield stresses as well as the geometric prop- erties of the simulated steel beams with a single opening adopted the values present in Redwood and Mc- cutcheon experiments [24] . All the modelled beams adopted a simply support configuration. The geometrical nonlinearity was evaluated using Updated Lagrangian Formulation. In this formulation, a large strain theory is used based on model deformed configuration. The considered non-linearities enable the development of these large strains at the steel beam web due to the stress redistribution that occurs along the web opening after the first yield onset. This strategy enables a detailed evaluation of the Vierendeel collapse represented by the suc- cessive formation of the plastic hinges on the “Tees”.
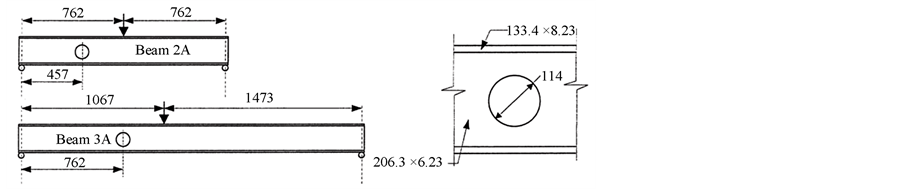
During the numerical investigation it was necessary to ensure that the model collapse was not associated to lateral torsional buckling or to a local buckling at the load application point or supports. This was made by re- stricting the lateral displacements of the top flange along the beam span and using transverse stiffeners at the load application point and supports. Figure 5 and Figure 6, present the models developed by Chung et al. [10] and Chung and Lawson [2] to simulate the steel beam with a single web opening.
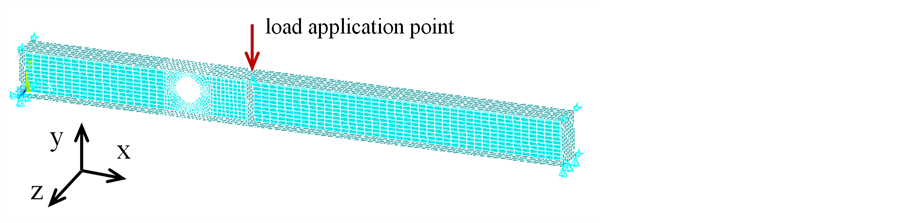
Tables 1-3 present the physical and geometrical characteristics of the beams numerically models by Chung et al. [10] and Chung and Lawson [2] , based on experiments performed by Redwood and McCutcheon [24] . The numerical results here presented were elaborated with the material and geometry used by Chung et al. [10] . A direct comparison of the obtained results with Chung et al. [10] results, can confirm the accuracy of the pro- posed finite element model that was later used in a subsequent parametric analysis of steel beams with web openings. The models adopted in the present investigation are depicted in Figure 7 and Figure 8.
The developed finite element models are similar to the models developed by Chung et al. [10] . The mesh was refined near the web opening to enable the model to accurately represent the effect related to the stress concen- tration, the onset of plasticity in the web and flanges as well as the hinge formation that characterises the Vier- endeel collapse mechanism. The beams supports were created aiming to reproduce simply support conditions. The boundary conditions used for this issue can be identified in Figure 7 and Figure 8, i.e., on the bottom left side, restrictions to displacements UX, UY and UZ and on the bottom right side, restrictions to displacements UY and UZ. The lateral bracing supports were used along the beam top flange to inhibit the lateral torsional buckling with restrictions to UZ displacements... The load application point as well as the transverse stiffeners used to avoid the local web buckling can also be clearly identified in Figure 7 and Figure 8, respectively.
Figure 5. Finite element model (beam 2A) presenting a Vierendeel mechanism collapse mode [10] .
Figure 6. Beam models geometry [10] .
Figure 7. Beam 2A finite element model [25] .
Figure 8. Beam 3A finite element model [25] .
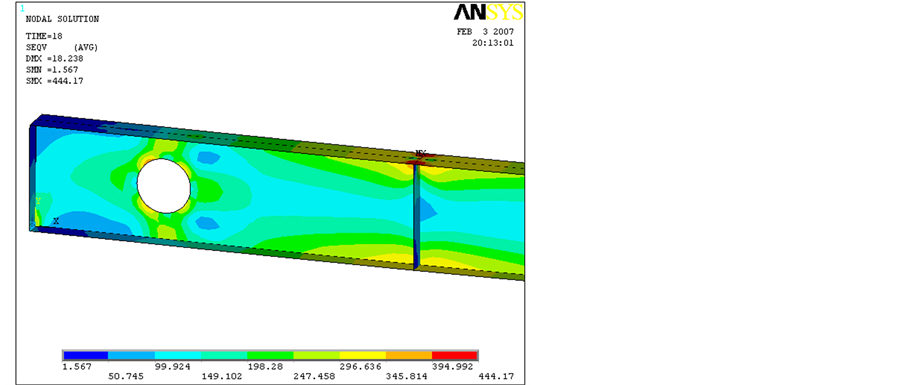
A comparison of the present paper results with Chung et al. [10] results, in terms of the yield distribution pat- terns on the beam web, near the openings, with an increase of the applied load can be seen in Figures 9-11. It can be observed that Chung et al. [10] models, for beam 2A are very similar to the present investigation results.
Table 1. Steel sections yield and ultimate stresses (in MPa).
Table 2. Steel sections geometrical properties.
Table 3. Modelled beam characteristics.
Both distributions also proved to be in agreement with the experiments made by Redwood and McCutcheon [24] validating the numerical modelling.
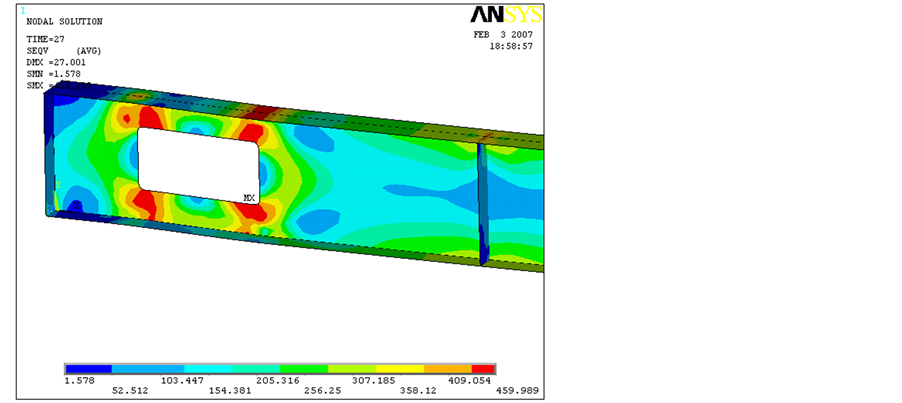
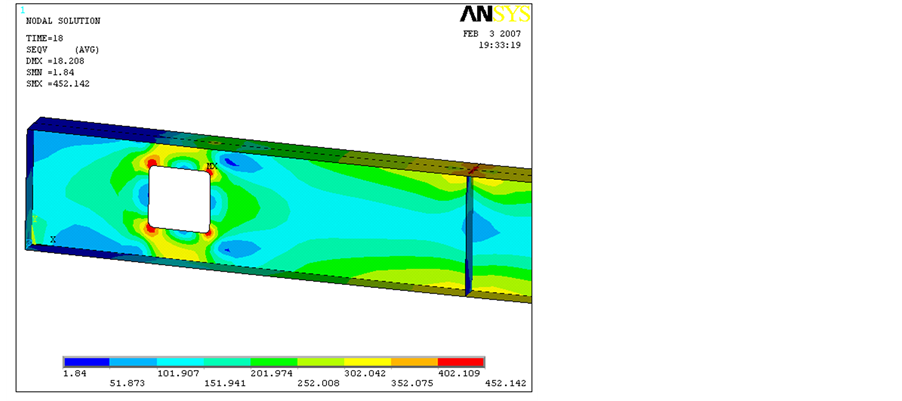
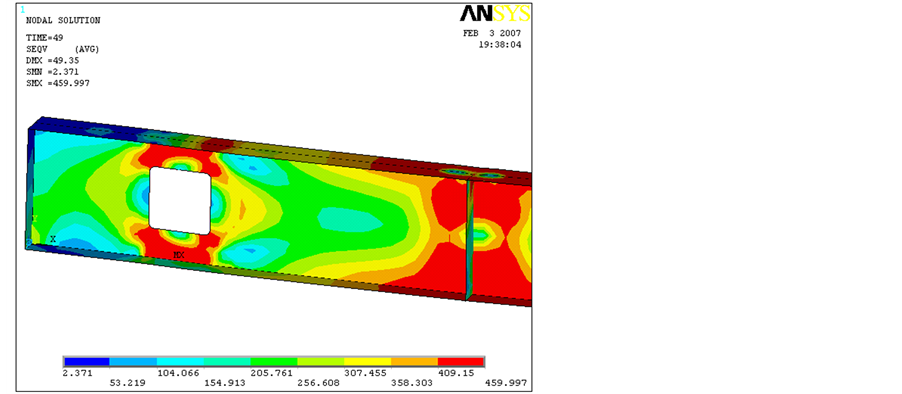
As previously highlighted by Chung et al. [10] it is interesting to observe the stress distribution near the per- forated section for beam 2A at the onset of yielding and at the collapse. The yielding begins at the web of the “Tees” at sections with α = 30˚ and α = −45˚ (see Figure 11). At the same time a shear yielding at the web of the “Tees” at sections with α = 0˚ is also noticeable. However, this yield does not generate a collapse mechanism and the beam is still able to sustain additional loads until the Vierendeel bending is sufficient to cause an exten- sive yielding on the “Tees”.
At the collapse, the “Tees” web and flanges at the higher moment section (HMS) present a considerable yielding distribution. Additionally, there is an extensive shear plasticity distribution at the web of the “Tees” at sections with α = 0˚. However, at the lower moment section (LMS) only the web of the “Tees” is yielded while the flange stress magnitude is limited to 60% of the yield stress. This fact results in beam 2A collapse being as- sociated to two plastic hinges at the higher moment section (HMS) and only two partial plastic hinges at the lower moment section (LMS). Probably this is due to the fact that at collapse an extensive yielding occurs on the “Ts” reducing the beam capacity to redistribute the stresses along the web opening. This observation are also in consonance with a study made by Chung et al. [22] , concerning the current design methods for this phenomenon in which not all the four plastic hinges are fully developed at collapse.
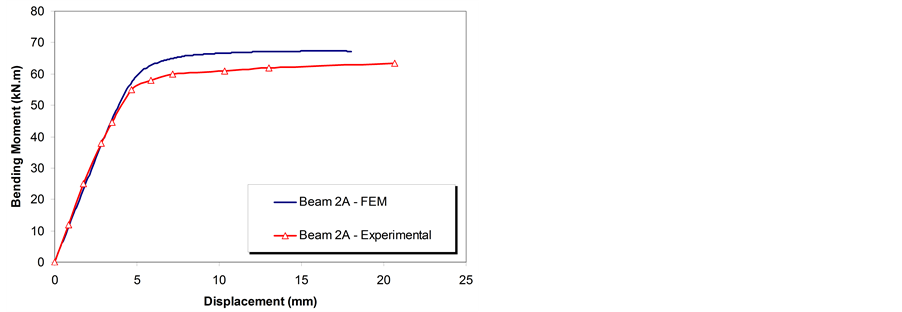
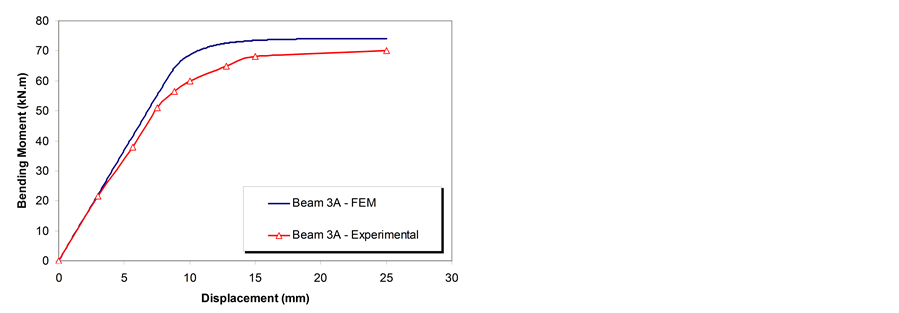
The calibration of the developed models was also made through comparative graphs containing the experi- mental results produced by Redwood and McCutcheon [24] . Figure 12 and Figure 13 depict bending moment at the centre of the web opening versus central span vertical deflection curves for beams 2A and 3A. The curves indicated that a reasonable agreement with the experiments was reached specially in the elastic range. On the plastic range a slight difference between the numerical and experimental results was observed. This difference can be attributed to the 5% strain hardening Young modulus adopted in the numerical models. Another reason could be related to the residual stresses induced by the welding/rolling processes or geometric that was not in- corporated in the numerical models. Geometric imperfections present in these beams can also be the cause for this difference. Table 4 presents a comparison of the experimental and numerical results for Beams 2A and 3A.
A finite element model for eight meter span cellular beams based on Bitar et al. [26] results was also made. The beam was made from an IPEA 450 profile with a S355 steel grade with eleven circular web openings with a 560 mm diameter, Figure 14. The holes centre to centre distance was equal to 700 mm. The fabrication processes in- creased the beam height to 710 mm. Table 5 exhibits the geometrical properties for the adopted IPEA 450 steel profile.
Table 4. Numerical and experimental model comparison.
Table 5. Numerical and experimental model comparison.
Figure 9. Beam 2A shear stress distribution at the perforated section (MPa).
The beam was symmetrically loaded at two points as can be observed in Figure 14. The boundary conditions were as described for Figure 7 and Figure 8. The experimental collapse load at each of the load application points was equal to 199.8 kN while the numerical collapse load was 185.3 kN. A 7.3% difference between ex- perimental and numerical models was observed indicating that the finite element model is adequate for the in- vestigated cellular beam. The failure was due to the formation of a plastic Vierendeel mechanism at the load ap- plication points such as presented in Figure 15.
The comparison of the entire single or multiple perforated beam simulated cases in terms of collapse load magnitude and bending moment ratios indicated a good agreement between the numerical and experimental re- sults validating the accuracy of the proposed numerical models.
Figure 10. Beam 2A normal stress distribution at the perforated section (in MPa).
Figure 10. Beam 2A normal stress distribution at the perforated section (in MPa).
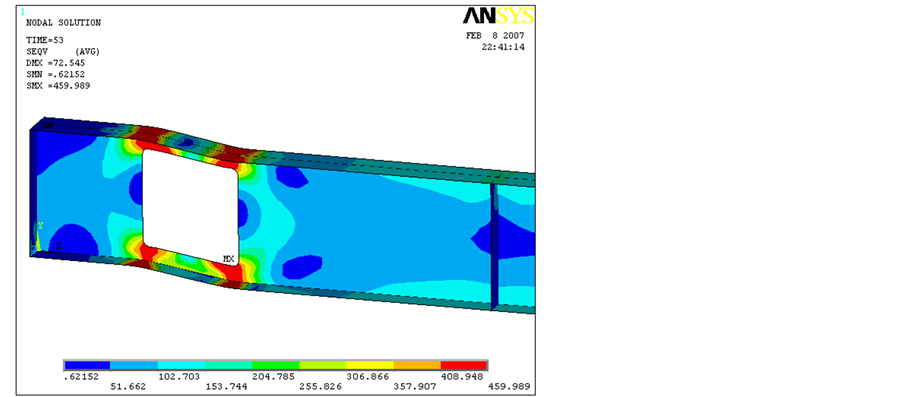
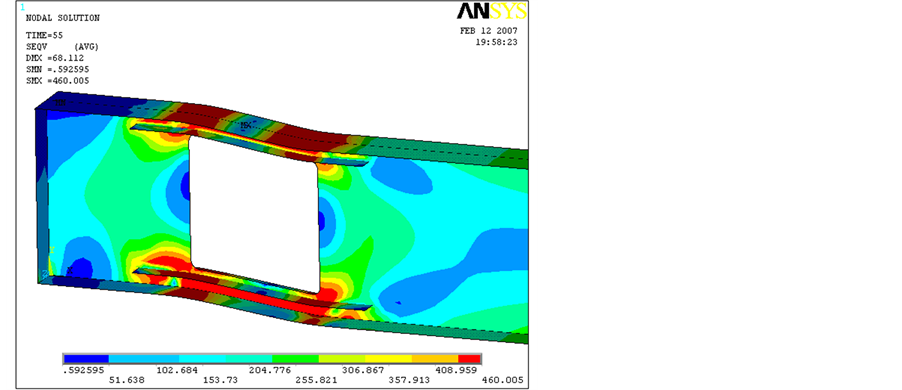
Figure 11. Beam 2A von Mises stress distribution at the perforated section (in MPa).
Figure 11. Beam 2A von Mises stress distribution at the perforated section (in MPa).
Figure 12. Beam 2A finite element and experimental model results comparison.
Figure 13. Beam 3A finite element and experimental model results comparison.
Figure 14. Cellular beam made of an IPEA 450 section (S355 steel).
Figure 15. Von Mises stresses at the collapse (in MPa).
4. Parametrical Analysis
The accurate results achieved in the simulations enable a comprehensive parametric analysis of steel beams with web openings to be performed [23] . An overview of the parameters investigated on the parametric analysis for the IPE500 and IPE750x137 steel profiles detailed in Table 5 can be observed in Table 6 and Table 7, respec- tively. An inspection of Table 6 and Table 7 identifies the investigated parameters, i.e. a) the steel profile size; b) the web opening location in relation to the beam span; c) the web opening diameter relation to the profile height; d) the beam span; e) the web opening geometry; and f) the concentrated load position in relation to the beam span. It should be observed that beams with rectangular openings were simulated adopting the opening length twice the size of its height. Table 6 and Table 7 also present for all the performed simulations their respective ulti- mate loads and associated failure modes. It should be mentioned that the results presented in Table 6 and Table 7 were compared to the design code provisions [4] previously presented in the second section of the present paper and will be further discussed in detail in the following paragraphs.
Table 6. Parametric study variables overview―IPE750x137 Profile.
Table 7. Parametric study variables overview. IPE500 Profile.
An inspection of the results obtained for the specimens 1 to 6, Table 6, and for the specimens 25 to 30, Table 7 indicated that opening geometry significantly influences the steel beams load carrying capacity. As expected the beams with rectangular openings presented the smaller ultimate loads. i.e. 30% less than their equivalent beams with square or circular openings. In these specimens the Vierendeel collapse mechanism was observed in all the beams with rectangular openings and was independent of the beam opening position on the span. It should also be pointed out that the beams with rectangular openings located at a point distancing 0.15 L (L is the beam span) from the supports reached ultimate loads less than their equivalent beam with rectangular openings located at a point distancing 0.6 L from the supports. This issue is easily explained by the fact that the Vieren- deel mechanism formation is intimately associated to the shear force magnitude at the opening i.e. increasing the shear force magnitude at the opening reduces the beam collapse load.
Beams with square openings presented a collapse mode combining the Vierendeel collapse mechanism with a load application point bending collapse. For these beams, openings located at a point distancing 0.60 L (where L represents the beam span) from the supports produced ultimate loads less than beams with openings at 0.15 L from the supports. This fact indicates that the bending stresses begin to play a significant part in theses beams ultimate loads.
Beams with circular openings presented two distinct collapse modes. The beams with openings located at a point distancing 0.15 L from the supports had their collapse associated to a load application point bending col- lapse. This type of collapse demonstrates that despite the higher shear force acting at the openings, their circular geometry enable the beams to sustain higher ultimate loads, similar to the ultimate loads of beams without openings and corroborating the conclusion that the presence of the opening did not influence the beam collapse load. Beams with circular openings located at 0.6 L from the supports had their collapse associated to an interac- tion of the Vierendeel mechanism and the load application point bending collapses.
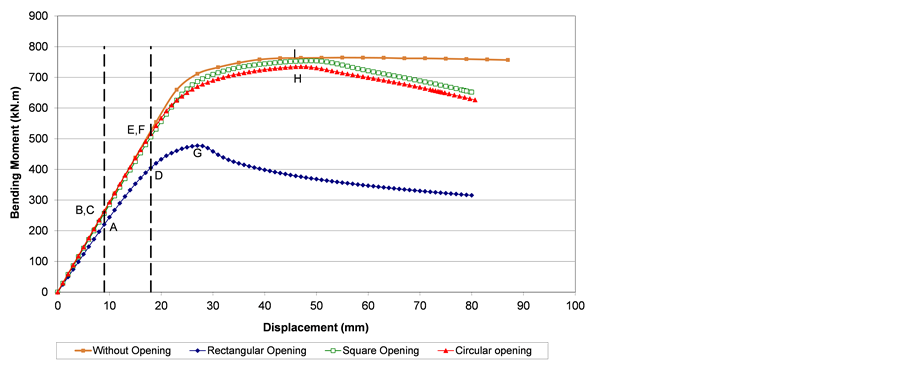
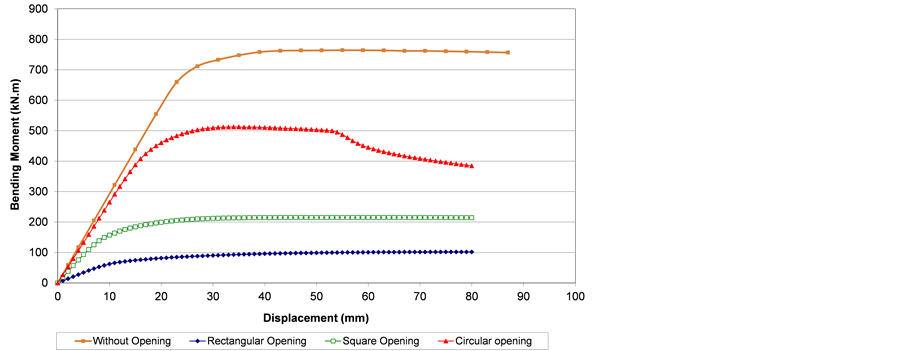
Figure 16 presents the variation of the bending moment at the web opening centre versus the load application point vertical displacement for specimens A, 1, 3 and 5, Table 6. From this figure it is possible to conclude that the higher ultimate moment is associated to the beam with a square opening closely followed by the beam with circular opening. On the other hand, a 35% reduction on the ultimate moment capacity was observed in the beam with a rectangular opening. The beams with square and circular openings presented a similar structural response and had their collapses associated to an interaction of the Vierendeel mechanism and the load application point bending collapses. Alternatively, the beam with a rectangular opening depicted a typical Vierendeel collapse mechanism illustrated by abrupt failure without the presence of a yield plateau.
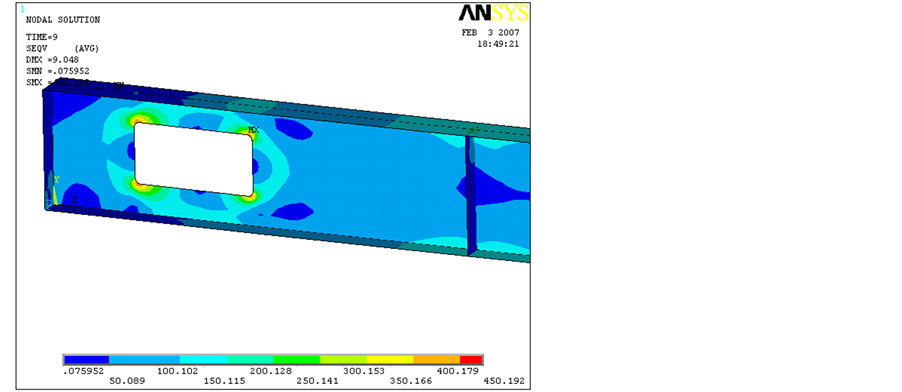
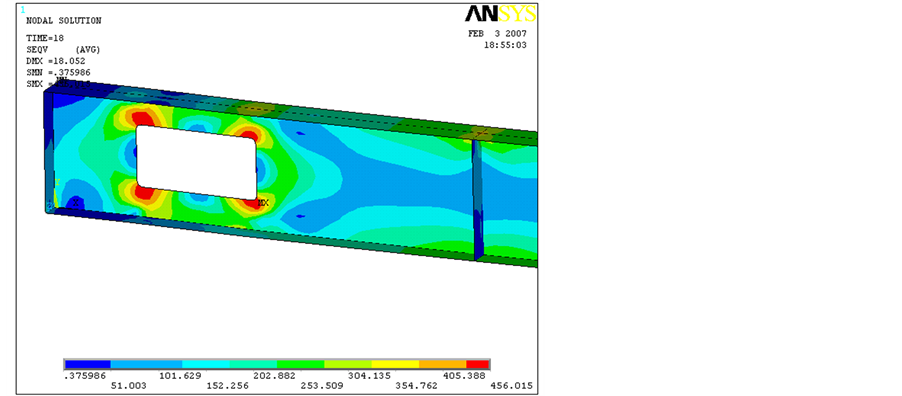
Figures 17-19 illustrate an evolution of the Von Mises stress distribution for specimens 1, 3 and 5 (Table 6). The compared load steps are depicted in Figure 16 by the letters “A” to “I” indicating load step magnitudes as- sociated to 9 mm vertical displacements (“A”, “B” & “C”), 18 mm vertical displacements (“D”, “E” & “F”), and to the ultimate bending moment (“G”, “H” & “I”), for beams with square, circular and rectangular openings, re- spectively.
Figures 17-19 indicated that despite the adopted corner concordance radius being equal to twice the web thickness, stress concentration point were formed at the corner of the openings of beams with square and rec- tangular geometries. This stress concentration increases and are redistributed throughout the web with an in- crease of the applied load till the phase were one or more plastic hinges are formed. The beams with rectangular opening geometries had their collapse associated to simple Vierendeel mechanisms. The collapse of beams with square openings was associated to an interaction of the Vierendeel mechanism and the load application point bending collapses. The beam with a circular opening tended to present a collapse associated to a load application point bending but could also present a collapse related to an interaction of the Vierendeel mechanism and the load application point bending if the load application point was situated near the web opening region.
An inspection of the numerical simulation referenced as specimens 7 to 12, Table 6, and specimens 31 to 36, Table 7, indicated a complete of their associated collapse modes when compared to the previously mentioned
Figure 16. Bending moment vs. vertical deflection curves.
Figure 17. Von Mises stress distribution associated to 9 mm, 18 mm vertical deflection and collapse due to a concentrated load (beam with a rectangular opening, Points A, D & G) (MPa).
Figure 18. Von Mises stress distribution associated to 9 mm, 18 mm vertical deflection and collapse due to a concentrated load (beam with a square opening, points B, E & H) (MPa).
Figure 19. Von Mises stress distribution associated to 9 mm, 18 mm vertical deflection and collapse due to a concentrated load (beam with a circular opening, points C, F & I) (MPa).
failures for specimens 1 to 6, Table 6, and specimens 25 to 30, Table 7. Specimens 7 to 12, Table 6, and specimens 31 to 36, Table 7, presented larger spans fact that significantly reduces the presence of Vierendeel mechanism failures favouring the occurrence of collapse mode combining the Vierendeel collapse mechanism with a load application point bending collapse. Only a single beam, with the load application point near the rec- tangular opening centre, presented a collapse exclusively associated to a Vierendeel mechanism. It is not diffi- cult to observe that similar ultimate loads were reached in all simulations, being close to the ultimate load of beams without openings. This assertive leads to the conclusion that, for this set of specimens, the presence of the opening was irrelevant for the beam collapse load prediction.
Alternatively, specimens 13 to 18, Table 6, and specimens 37 to 42, Table 7, only presented Vierendeel col- lapse mechanisms regardless of the location or geometry of the opening. On the other hand, a significant varia- tion of the collapse load magnitude was observed. The beam with a circular opening geometry achieved the higher ultimate load and was followed by the beams with square and rectangular openings. Another interesting point was that even the beam with a circular opening presented an ultimate load significantly reduced (30% less) when compared to beams without openings. These results of these simulations indicated that beams with open- ings around 75% of the beam height can significantly reduce their load carrying capacities regardless of their opening geometry.
Figure 20 illustrates an evolution of the Von Mises stress distribution at the ultimate bending moment for specimens 13, 15 and 17, Table 6. From these results it is possible to conclude that in all the beams the collapse was associated to the formation of four plastic hinges at the opening extremities, clearly characterising the Vierendeel collapse mechanism.
Figure 21 presents the variation of the bending moment at the web opening centre versus the load application point vertical displacement for specimens 13, 15 and 17, Table 6. From this Figure it is possible to conclude that all the beams presented a considerable yielding before collapse. This was due to a crescent stress redistribution that occurred at the beam web opening edge region up to the formation of the plastic hinges.
It was also possible to observe that the beam with a circular opening presented an ultimate load five and two and a half times the ultimate load associate to beams with rectangular and square openings, respectively. These results can be attributed to the better stress redistribution achieved with the circular opening configuration that led reduction on the stress concentration at the beam web opening edge region. It was also possible to notice that beams with rectangular and square openings were associated to high stress concentration at the beam web open- ing edge region corroborating the idea that a concordance radius equal to two times the web thickness, used at those regions was appropriate.
The Vierendeel mechanism was still the main collapse mode associated to specimens 19 to 24, Table 6, and specimens 43 to 48, Table 7, despite the adopted ten meter beam span. Initially it was expected that with an in- crease of the beam span the Vierendeel collapse mechanism tended to be less significant than the other relevant collapse modes. However this proved not to be the case and led to the conclusion that beams with openings around 75% of the beam height, regardless of the adopted opening geometry, would fail by a Vierendeel col- lapse mechanism. One more time the better structural performance was achieved by the beam with a circular opening followed by the beams with rectangular and square openings.
The parametric study results also demonstrated that insignificant differences were found when using the IPE500 or the IPE750x137 steel profiles. This implies that, for these profile range, the differences in structural response for beams with web openings proved to be irrelevant.
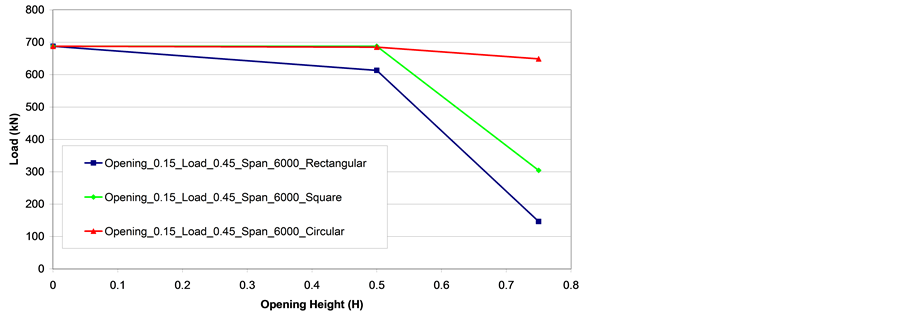
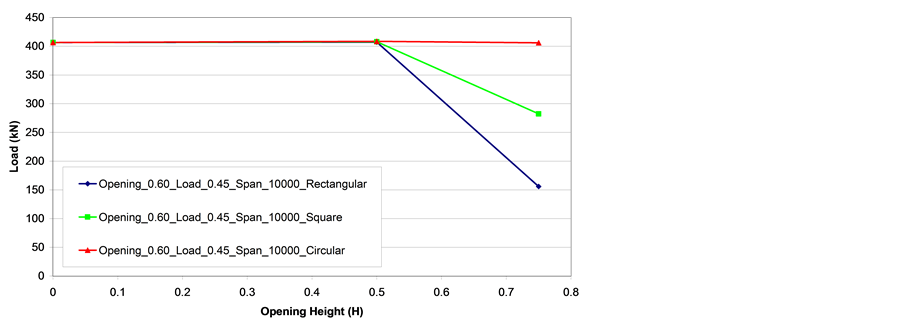
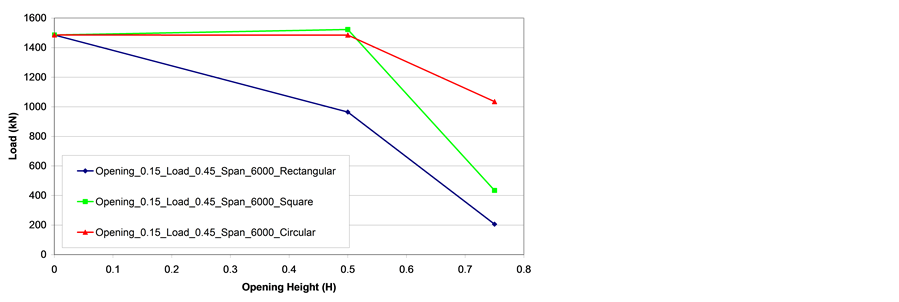
Figure 22 and Figure 23 depict ultimate load versus the opening to web height ratio curves for the IPE500 steel profile. From these graphs it is possible to observe that for a six meter span and a web opening equal to 0.5 H (H is the opening height) the beams with circular and square opening geometries presented similar ultimate loads to the beam without openings proving that the web opening presence was irrelevant. Alternatively, the beam with a rectangular opening with a six meter span and a web opening equal to 0.5 H (H is the opening height) showed a significant reduction on its load carrying capacity. This fact shows that beams with larger opening can have their structural capacity penalised since their associate opening geometry configurations contribute for a premature onset of the Vierendeel collapse mechanism.
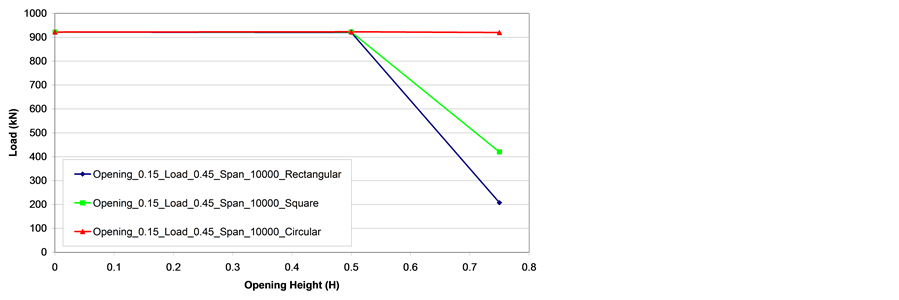
For a ten meter span and a web opening equal to 0.5 H all the beams with openings presented similar ultimate loads to the beam without openings proving that the web opening presence was one more time irrelevant and that an increase of the beam span reduces the relevance of the Vierendeel mechanism ultimate limit state. An- other important observation was that the beam with a circular opening equal to 0.75 H (and a ten meter span)
Figure 20. Von Mises stress distributions associated to a collapse due to a concentrated load (beams with rectangular, square and circular openings without stiffeners) (MPa).
Figure 21. Bending moment vs. vertical deflection curves.
Figure 22. Ultimate load vs. opening height curves―IPE500―part I.
presented an ultimate load equal to the beam without openings regardless of the opening location along the beam span.
Table 8 and Table 9 present a comparison of the ultimate loads determined in finite element analysis and their counterparts evaluated using the analytical tool present in Darwin [4] for IPE750x137 and IPE500 profiles, respectively. The results indicate that the beams collapse modes associated to Vierendeel mechanism exhibit the value R, evaluated according to equation 1, close to 1.0.
When the beams collapse modes are associated to the load application point location, these beams presented the R values not so close to the unity as the ones which failed by Vierendeel mechanism. These results should be expected since the provisions given by the moment-shear interaction curve consider the cross section reduction
Figure 23. Ultimate load vs. opening height curves―IPE500―part II.
at the centre of the opening and are suitable for the design of steel beams with web openings. Hence, the beams that failed by Vierendeel mechanism exhibit values of R quite close to or higher than 1.0, while the beams that collapsed exclusively by bending presented values of R lower than 1.0 showing that the hole presence was not responsible for the collapse.
Additionally, it should be observed that the beams which failed exclusively by Vierendeel mechanism pre- sented the values of R generally higher than 1.0. This could be explained by the fact that the finite element mod- els used to evaluate the ultimate resistance of the beams with web openings, present material non-linearity through a bilinear elastoplastic response with a 5% strain hardening. This fact implies that the ultimate loads of the finite element models were higher than the ones achieved by the provisions from Darwin [4] .
It should be noted that the moment-shear interaction curve presented in Darwin [4] was calibrated to steel beams with maximum height web openings equal to 70% of the cross section total height. This clear scope limi- tation indicates that the results for the beams with web opening height beyond the scope of validity of the mo- ment-shear interaction curve should be interpreted with caution.
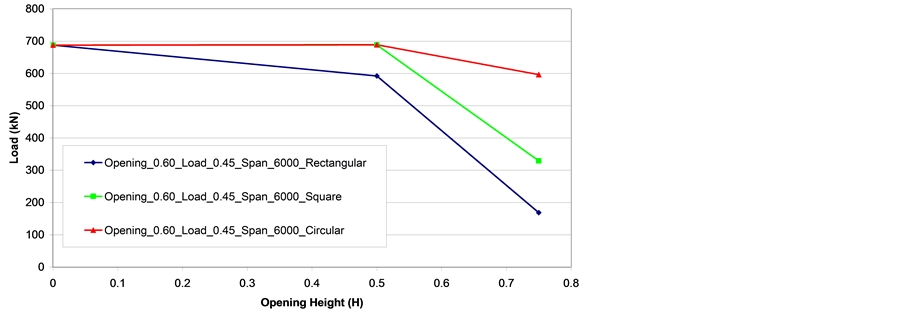
Figure 24 and Figure 25 present ultimate load versus the opening to web height ratio curves for the IPE750x137 steel profile. From these graphs it is possible to observe that, for a six meter span and a web opening equal to 0.5 H, the beams with circular and square opening geometries presented almost similar ultimate loads to the beam without openings. On the other hand, the beam with a rectangular opening, a six meter span and a web opening equal to 0.5 H, showed a significant reduction on its load carrying capacity. The reduction in load carrying capacity was even more pronounced for all the beams with a six meter span and a web opening equal to 0.75 H (H is the opening height). Beams with a ten meter span one more time proved the structural efficiency of the beams with circular openings presenting higher ultimate loads than the other investigated opening geometries.
As previously mentioned the use of an appropriate concordance radius at the beam web opening edge region is extremely important for beams with square and rectangular openings since it reduces the stress concentration
Table 8. Design code validation―IPE750x137 Profile.
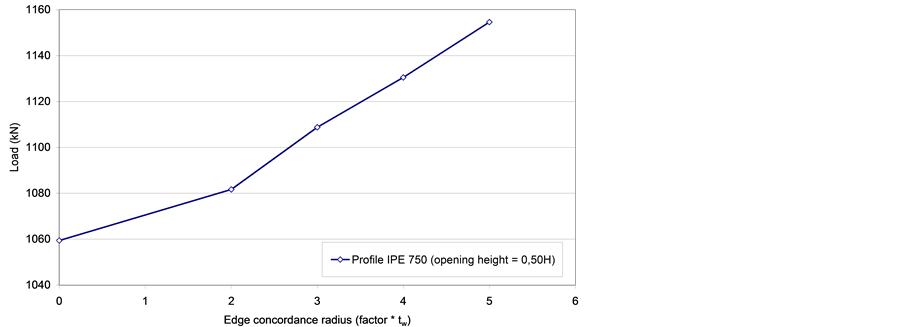
around those regions and contributes for a better stress redistribution along the steel beam web. Figure 26 de- picts an ultimate load versus opening edge concordance radius (in terms of the web thickness) curve.
It can be easily observed that an increase of opening edge concordance radius was very efficient for increas- ing the collapse loads beam with rectangular openings. An IPE500 with a rectangular opening height equal to 0.5 H, a six meter span and an opening edge concordance radius equal to five times the web thickness, presented a 9% increase of its ultimate load when compared to beams with smaller concordance radius, Figure 26. This fact serves to corroborate the importance of this structural detail in the web stress redistribution of beams with web openings.
Figures 22-25 demonstrated that beams with square and rectangular opening heights equal to 0.75 H had their structural capacities severely compromised. Despite this fact, there are situation where the use of these openings cannot be avoided. For these cases the use of longitudinal stiffeners welded at the horizontal edges of the web openings are strongly suggested by the structural best practice and design standards. Aiming to verify the struc- tural efficiency of these stiffeners three beams were simulated with and without stiffeners. They had the same characteristics of some of the numerical simulations performed in the parametric analysis (i.e. specimens
Table 9. Design code validation―IPE500 Profile.
13, 15 & 17). The longitudinal stiffeners were modelled with the geometrical characteristics suggested by Chung and Lawson [2] , and presented in Table 10, and are illustrated in Figure 27.
Figure 28 indicates that the presence of the longitudinal stiffeners enables a better stress redistribution along the web openings (compare to the results depicted in Figure 20) contributing for an increase of the beams load carrying capacity. Despite this beneficial effect the Vierendeel mechanism was still the controlling collapse mode for these beams.
Table 11 presents a comparison of the ultimate loads for beams with and without stiffeners for the configura- tion related to specimens 13, 15 & 17. It could be observed that the stiffeners were very efficient contributing for a substantial improvement of the ultimate loads of beams with square and rectangular openings. Even the beam with a circular opening presented an increase of the ultimate load that cannot be discarded. At this point it is fair to mention, one more time, that the effects of the residual stressed due to the welded or rolling steel profile pro- duction were not incorporated in the non-linear numerical analysis.
It could be observed that the use of longitudinal stiffeners along the opening region presented a considerable advantage when compared to beams with non-stiffened web opening solutions. The stiffened solutions enabled
Figure 24. Ultimate load vs. opening height curves―IPE750―Part I.
Figure 25. Ultimate load vs. opening height curves―IPE750―Part II.
Figure 26. Ultimate load vs. corner radius at the opening edge curve.
Figure 27. Longitudinal stiffener recommendations [2] .
Table 10. Stiffener geometry characteristics.
Table 11. Beams with and without longitudinal stiffeners comparison in terms of collapse loads.
an increase of the beam ultimate bending capacity around three and two times the unstiffened solutions for beams with rectangular and square openings, respectively. When a comparison of the stiffened and unstiffened
Figure 28. Von Mises stress distributions associated to a collapse due to a concentrated load (beams with rectangular, square and circular openings with longitudinal stiffeners) (MPa).
solutions was made even the beams with circular openings were associated to a 20% increase of the beam ulti- mate bending capacity.
5. Final Remarks
This paper presented finite element models using the ANSYS software [25] to investigate the structural response of steel beams with web openings in terms of stress distributions, collapse load magnitude and associated failure modes. The analysis incorporated geometric and material non-linearities and were calibrated against numerical and test results to validate the proposed finite element models producing reliable results. The investigation also contemplated the simulations of beams with a series of openings distributed all over their length, i.e., cellular beams. The simulations were centred at the evaluation of the different steel beams with web openings failure mechanisms and the main reasons for that collapses proving to be in accordance with the experiments present in the literature.
The present investigation proved the structural efficiency of unstiffened steel beam with circular web open- ings (five and two and a half) when compared to their equivalent unstiffened solutions with square and rectan- gular openings.
The beams with rectangular openings presented the smaller ultimate loads. i.e. 30% less than their equivalent beams with square or circular openings. In these specimens the Vierendeel collapse mechanism was observed in all the beams with rectangular openings and was independent of the beam opening position on the span. Beams with square openings presented a collapse mode combining the Vierendeel collapse mechanism with a load application point bending collapse.
Beams with circular openings presented two distinct collapse modes. The beams with openings located at a point distancing 0.15 L from the supports had their collapse associated to a load application point bending col- lapse.
When large spans were used, this fact significantly reduces the presence of Vierendeel mechanism failures fa- vouring the occurrence of collapse mode combining the Vierendeel collapse mechanism with a load application point bending collapse.
It was also presented a comparison of the ultimate loads determined in finite element analysis and their coun- terparts evaluated using the analytical tool present in Darwin [4] for IPE750x137 and IPE500 profiles, respec- tively. The beams that failed by Vierendeel mechanism exhibit values of R quite close to or higher than 1.0, while the beams that collapsed exclusively by bending presented values of R lower than 1.0 showing that the hole presence was not responsible for the collapse.
The use of adequate edge concordance radius in beams with rectangular and square openings is very efficient for better distributing steel beam web stresses since it reduces the stress concentration at these points. Using an edge concordance radius equal to five times the web thickness in a six meter span beam (IPE750x137) with a rectangular opening height equal to 0.5 H increased in 9% its ultimate load.
According to the results presented in Figures 22-25, the use of longitudinal stiffeners welded to horizontal edge of web openings is strongly recommended for beams with opening heights greater than half of the beams height i.e. 0.5 H. The welded longitudinal stiffeners enable a better stress redistribution around the opening re- gion contributing for an increase of the beams ultimate load carrying capacity. The present investigation con- firmed that their adoption can double or even triple the ultimate load of beams with rectangular and square opening heights equal to three quarters of the beams height i.e. 0.75 H, respectively.
Acknowledgements
The authors gratefully acknowledge the financial support provided by the Brazilian National and State Scientific and Technological Developing Agencies: CNPq, CAPES and FAPERJ.
References
- Chung, K.F. and Ko, C.H. (2002) Harmonization on Practical Design of Steel and Composite Beams with Large Web Openings for Full Integration with Building Services. Proceedings of the Second Structural Engineering World Congress, Yokohama, 9-12 October 2002 (CD Publication).
- Chung, K.F. and Lawson, R.M. (2001) Simplified Design of Composite Beams with Large Web Openings to Eurocode 4. Journal of Constructional Steel Research, 57, 135-163. http://dx.doi.org/10.1016/S0143-974X(00)00011-0
- Lawson, R.M. (1987) Design for Openings in the Webs of Composite Beams. CIRIA/Steel Construction Institute, CIRIA Special Publication and SCI Publication 068, Ascot.
- Darwin, D. (1990) Steel and Composite Beams with Web Openings. Steel Design Guide Series, Vol. 2. AISC-American Institute of Steel Construction, Chicago.
- Redwood, R.G. and Cho, S.H. (1993) Design of Steel and Composite Beams with Web Openings. Journal of Constructional Steel Research, 25, 23-41. http://dx.doi.org/10.1016/0143-974X(93)90050-3
- Oehlers, D.J. and Bradford, M.A. (1995) Composite Steel and Concrete Structural Members: Fundamental Behaviour. Kidlington, Oxford.
- Chung, K.F., Ko, C.H. and Wang, A.J. (2005) Design of Steel and Composite Beams with Web Openings―Verifica- tion Using Finite Element Method. Steel and Composite Structures, 5, 203-233. http://dx.doi.org/10.12989/scs.2005.5.2_3.203
- Ko, A.C.H. and Chung, K.F. (2002) A Review of Recent Developments on Design of Perforated Beams. Proceedings of the Third International Conference on Advances in Steel Structures, Hong Kong, 9-11 December 2002, 121-128.
- Wang, A.J. and Chung, K.F. (2008) Advanced Finite Element Modelling of Perforated Composite Beams with Flexible Shear Connectors. Engineering Structures, 30, 2724-2738. http://dx.doi.org/10.1016/j.engstruct.2008.03.001
- Chung, K.F., Liu, T.C.H. and Ko, A.C.H. (2001) Investigation on Vierendeel Mechanism in Steel Beams with Circular Web Openings. Journal of Constructional Steel Research, 57, 467-490. http://dx.doi.org/10.1016/S0143-974X(00)00035-3
- Lakusic, V.T., Dzeba, I. and Androic, B. (2008) The Buckling Curve for Lateral-Torsional Buckling Resistance of Cas- tellated Beams. Eurosteel-5th European Conference on Steel and Composite Structures, Graz, 3-5 September 2008, 1587-1592.
- CEN-European Committee for Standardization (1998) Eurocode 3―Design of Steel Structures―Part 1-1: General Rules and Rules for Buildings. ENV 1993-1-1:1992/A2 Annex N, Brussels.
- CEN-European Committee for Standardization (2005) Eurocode 3―Design of Steel Structures―Part 1-1: General Rules and Rules for Buildings. ENV 1993-1-1, Brussels.
- CEN-European Committee for Standardization (1992) Eurocode 3―Design of Steel Structures―Part 1-1: General Rules and Rules for Buildings. EN 1993-1-1, Brussels, Belgium and Not ENV 1993-1-1, Brussels, Belgium.
- Radic, I., Markulak, D. and Varevac, D. (2008) Numerical Simulation of Lateral Stability. Eurosteel-5th European Con- ference on Steel and Composite Structures, Graz, 3-5 September 2008, 1593-1598.
- Basher, M.A., Shanmugam, N.E. and Khalim, A.R. (2009) Web Openings in Horizontally Curved Composite Plate Girders. Journal of Constructional Steel Research, 65, 1694-1704. http://dx.doi.org/10.1016/j.jcsr.2009.02.009
- Hagen, N.C., Larsen, P.K. and Aalberg, A. (2009) Shear Capacity of Steel Plate Girders with Large Web Openings, Part I: Modeling and Simulations. Journal of Constructional Steel Research, 65, 142-150. http://dx.doi.org/10.1016/j.jcsr.2008.03.014
- Hagen, N.C. and Larsen, P.K. (2009) Shear Capacity of Steel Plate Girders with Large Web Openings, Part II: Design Guidelines. Journal of Constructional Steel Research, 65, 151-158. http://dx.doi.org/10.1016/j.jcsr.2008.03.005
- Lagaros, N.D., Psarras, L.D., Papadrakakis, M. and Panagiotou, G. (2008) Optimum Design of Steel Structures with Web Openings. Engineering Structures, 30, 2528-2537. http://dx.doi.org/10.1016/j.engstruct.2008.02.002
- Lian, V.T. and Shanmugan, N.E. (2003) Openings in Horizontally Curved Plate Girder Webs. Thin-Walled Structures, 41, 245-269. http://dx.doi.org/10.1016/S0263-8231(02)00090-3
- Liu, T.C.H. and Chung, K.F. (2003) Steel Beams with Large Web Openings of Various Shapes and Sizes: Finite Element Investigation. Journal of Constructional Steel Research, 59, 1159-1176. http://dx.doi.org/10.1016/S0143-974X(03)00030-0
- Chung, K.F., Liu, T.C.H. and Ko, A.C.H. (2003) Steel Beams with Large Web Openings of Various Shapes and Sizes: An Empirical Design Method Using a Generalised Moment-Shear Interaction Curve. Journal of Constructional Steel Research, 59, 1177-1200. http://dx.doi.org/10.1016/S0143-974X(03)00029-4
- Rodrigues, F. (2007) Comportamento estrutural de vigas de aço e mistas com aberturas na alma. Dissertation, UERJ- State University of Rio de Janeiro, Rio de Janeiro. (in Portuguese)
- Redwood, R.G. and Mccutcheon, J.O. (1968) Beam Tests with Unreinforced Web Openings. Journal of the Structural Division, 94, 1-17.
- ANSYS Academic Research. Swanson Analysis Systems, Inc. (2008) Version 11.0. Basic Analysis Procedures. 2nd Edition, Houston.
- Bitar, D., De Marco, T. and Martin, P.O. (2005) Steel and Composite Cellular Beams―Novel Approach for Design Based on Experimental Studies and Numerical Investigations. Eurosteel 2005, 4th European Conference on Steel and Composite Structures, Maastricht, 1.10.1-1.10.8.
List of Symbols
Latin Symbols
As = stiffener area;
Af = beam flange area;
D = beam section height;
ds = stiffener width;
d0 = hole height;
H = beam section height;
HMS = high moment side of the web openings separately;
L = beam span;
LMS = low moment side of the web openings separately;
MEXP = experimental bending moment;
MFEM = numerical bending moment obtained in finite element analysis;
Mm = bending moment resistance;
Mn = actual bending moment present at beam centre span;
Mo,Sd = global bending moment;
MSd = global bending moment;
MT = bending moment due to global shear force transmitted along the opening length;
NT = axial force due to global bending moment;
py = material yielding limit;
R = ratio between the factored load to the section design capacity at an opening;
t = web thickness;
ts = stiffener thickness;
Vm = shear force resistance;
Vn = actual shear force present at beam centre span;
Vo,Sd = global shear force;
VSd = global shear force;
VT = shear force due to global shear force.
Greek Symbols
α―angle where the yielding begins at the web of the “Tees” sections;
ϕ―load and resistance safety factors.
NOTES
*Corresponding author.