Engineering
Vol.6 No.9(2014), Article
ID:48564,10
pages
DOI:10.4236/eng.2014.69054
A New Characterization Approach of Weld Nugget Growth by Real-Time Input Electrical Impedance
Yoke-Rung Wong*, Xin Pang
School of Mechanical & Aerospace Engineering, Nanyang Technological University, Singapore City, Singapore
Email: *wong0663@e.ntu.edu.sg
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2014; revised 20 June 2014; accepted 3 July 2014
ABSTRACT
The in-process changes of weld nugget growth during the Resistance Spot Welding were investigated based on the resistance of input electrical impedance. To compute the time varying resistance of input electrical impedance, the welding voltage and current signals are measured simultaneously and then converted into complex-valued signals by using Hilbert transform. Comparing with the dynamic contact resistance as reported in literature, it showed that the time varying resistance of input electrical impedance can be accurately correlated with the physical changes of weld nugget growth. Therefore, it can be used to characterize the in-process changes of weld nugget growth. Several new findings were reported based on the investigation of spot welds under no weld, with and without weld expulsion conditions.
Keywords:In-Process, Input Electrical Impedance, Dynamic Contact Resistance, Weld Nugget, Hilbert Transform

1. Introduction
Resistance Spot Welding (RSW) has been broadly used for the structural joints due to its advantages such as easy-to-use, low cost, clean working environment and short process time. In practice, a weld nugget is formed at the sheet-to-sheet interface (faying interface) of metal sheets due to the heat generation by the resistances to the flow of high electric current within a short period of time. During the welding process, electrode force is applied through the electrodes to bring the metal sheets into contact. On the other hand, water is used to cool down the electrodes (as shown in Figure 1).
The RSW is a coupled electrical-thermal-mechanical process which involves heat generation due to the presence of electric current and resistances according to Joule’s Law and the weld nugget growth as a result of metal melting [1] [2] . Therefore, the RSW process is a dynamic and complicated system which requires real time measurement for system characterization. In order to investigate the dynamic behavior of RSW process, the dynamic contact resistance was firstly introduced by Dickinson et al. [3] .
As shown in Figure 1, the dynamic contact resistance measured during the welding process is the summation of resistances, which can be distinguished into 4 groups: 1) R1 and R7, electrode resistances; 2) R3 and R5, bulk resistances; 3) R2 and R6, electrode to sheet interface resistances; 4) R4, contact resistance at sheet-to-sheet interface (faying interface). Dickinson et al. divided the contact resistance into 6 stages in order to characterize the weld nugget growth (see Figure 2). At Stage a, the metal sheets are in intimate contact as a result of material softening and collapse of surface contaminants at the faying interface. It causes a rapid drop in the resistance. However, the resistance stops to reduce further because the resistivity of metal increases as temperature is increasing at Stage b. Due to the continuous raising of temperature, the resistance reaches its maximum point at Stage d. Once the melting temperature is reached, the metal starts to melt at the faying interface and a weld nugget is formed. At Stage e, the surface indentation at the electrode to sheet interface causes the resistance to reduce gently. In case of weld expulsion, the ejection of molten metal from the weld nugget results into a sudden drop of resistance at Stage f.
To investigate the in-process changes of weld nugget growth, this dynamic contact resistance has to be a time-varying curve. However, Gedeon et al. [4] revealed that it is difficult to obtain such dynamic curve due to the presence of inductive noise in the welding system. In order to overcome this problem, some researchers
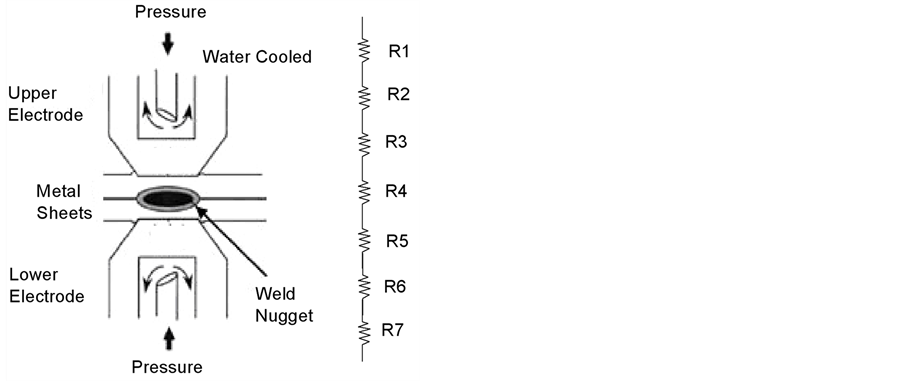
Figure 1. Schematic diagram of RSW.
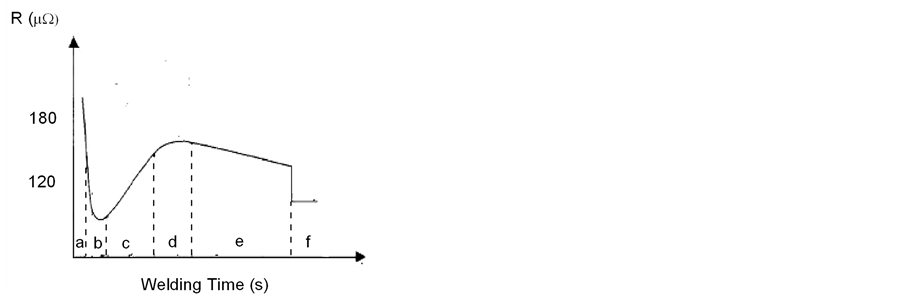
Figure 2. Dynamic contact resistance curve.
suggested that the instantaneous voltage is divided by the instantaneous current when the current reaches its peak value and then joins these resistance points from each half cycle to form the resistance curve. In this case, substantial error is unavoidable as a result of linear curve fitting approach.
In 2002, Cho and Rhee [5] developed a technology to obtain the primary dynamic resistance in primary circuit of welding machine. They claimed that this dynamic resistance can reflect the dynamic contact resistance in the secondary circuit of welding machine which is measured in an in-process system environment. However, the primary dynamic resistance is still obtained based on the instantaneous voltage and current measured at the primary circuit of welding machine and therefore the accuracy is poor. On the other hand, Wang and Wei [6] presented a numerical solution to predict the dynamic contact resistance based on the temperature distribution. Garza and Das [7] also proposed a method using Recursive Least Squares (RLS) algorithm to estimate the dynamic contact resistance. Both methods claimed that the predicted dynamic contact resistance is accurate and in-situ. Later in 2004, however, both results were reviewed by Tan et al. [8] and found that the first peak of resistance is not located exactly at the beginning of welding process when he investigated the relationship between the dynamic contact resistance with the micro-structural change of Ni sheets by small scale RSW. Instead, the first peak happens sometime after the welding process is started. In the paper, they suspected that the different location of first peak in dynamic contact resistance curve by AC current weld of large scale RSW is due to the high current increasing rate and thick surface film of metal sheets.
Recently, the use of input impedance as the monitoring signature for manufacturing processes has been in focus for ultrasonic welding [9] , wire bonding [10] and micro drilling [11] . Furthermore, the development of realtime quality monitoring method has been done successfully for RSW based on the input electrical impedance of RSW [12] . They reported that the resistance of input electrical impedance is more accurate than the dynamic contact resistance because it is a time varying resistance curve which is directly measured during the welding process. Through pattern recognition and classification process, several features of the resistance of input electrical impedance were correlated non-destructively with the weld quality by employing an Artificial Neural Network (ANN) model. Since the correlation of the weld quality with the features of resistance of input electrical impedance was only done by ANN model, it was not able to reveal the in-process changes of weld nugget growth. As an extension of previous work reported in [12] , a detail study of the relationship between the resistance of input electrical impedance with the dynamic changes of weld nugget growth and the underlying arguments will be investigated and discussed in this paper.
2. Input Electrical Impedance of RSW, 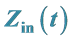
According to Ling et al. [12] , the purpose of using Hilbert transform is to obtain the analytic voltage and current signal so that the time varying input electrical impedance can be computed. The input electrical impedance, 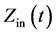 is calculated by taking the quotient of voltage to current signal in their analytic forms:
is calculated by taking the quotient of voltage to current signal in their analytic forms:
 (1)
(1)
 (2)
(2)
which the second term of the equations is the imaginary part of the real-valued signal, voltage  and current
and current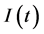 , obtained by performing Hilbert transform [13] . Basically, the Hilbert transform is defined as
, obtained by performing Hilbert transform [13] . Basically, the Hilbert transform is defined as
 (3)
(3)
where 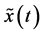 is the convolution integral of any real-valued signal,
is the convolution integral of any real-valued signal, 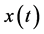 and
and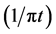 . In practice, the product of Hilbert transform can be obtained easily when the convolution integral is done in frequency domain.
. In practice, the product of Hilbert transform can be obtained easily when the convolution integral is done in frequency domain.
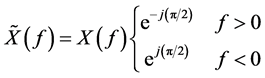 (4)
(4)
where 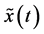 is the Fourier transform of
is the Fourier transform of 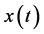 shifted by
shifted by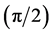 . In other words, the product of Hilbert transform is the original signal shifted by +90˚. After that, the
. In other words, the product of Hilbert transform is the original signal shifted by +90˚. After that, the 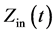 is obtained as [14] :
is obtained as [14] :
 (5)
(5)
In the above, the first term of  is known as real part or resistance of
is known as real part or resistance of 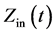 and the second term is the imaginary part or reactance of
and the second term is the imaginary part or reactance of . As compared to the conventional method for impedance calculation by using Fast Fourier Transform (FFT), the Hilbert transform allows the complex-valued signals,
. As compared to the conventional method for impedance calculation by using Fast Fourier Transform (FFT), the Hilbert transform allows the complex-valued signals,  and
and 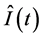 to be processed in time domain so that the time variations of
to be processed in time domain so that the time variations of  is retained. Furthermore, the
is retained. Furthermore, the 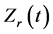 is indeed the dynamic resistance and inherently isolated from the influence of inductive noise which is reflected by the
is indeed the dynamic resistance and inherently isolated from the influence of inductive noise which is reflected by the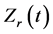 . Therefore, a unique method for measuring the accurate dynamic contact resistance is developed.
. Therefore, a unique method for measuring the accurate dynamic contact resistance is developed.
3. Experimental Setup
Figure 3(a) and Figure 3(b) show the experimental setup to measure the  of RSW. A 50 Hz single phase AC, 75 KVA rated power pedestal type welding machine was used. For acquiring the welding voltage and current signal, a simple BNC to crocodile clip cable and a toroidal coil type current probe (AmpFlex, Flexible AC Current Probes, 10000-24-2-0.1) were used. The clip cable was attached to the electrodes and the current probe was hooked on the copper wire at the secondary circuit of the welding machine. These signals were then acquired simultaneously by the DAQ system (Nicolet Scope, 12 bits, 8 channels) at 10 kHz of sampling rate. Analog filters were used before the signal sampling process and their cutoff frequency was set at 100 Hz to avoid signal aliasing. Bi-polar (windows) triggering mode was used and the sampling period was set as same length as the welding time in order to prevent signal leakage at the first welding cycle.
of RSW. A 50 Hz single phase AC, 75 KVA rated power pedestal type welding machine was used. For acquiring the welding voltage and current signal, a simple BNC to crocodile clip cable and a toroidal coil type current probe (AmpFlex, Flexible AC Current Probes, 10000-24-2-0.1) were used. The clip cable was attached to the electrodes and the current probe was hooked on the copper wire at the secondary circuit of the welding machine. These signals were then acquired simultaneously by the DAQ system (Nicolet Scope, 12 bits, 8 channels) at 10 kHz of sampling rate. Analog filters were used before the signal sampling process and their cutoff frequency was set at 100 Hz to avoid signal aliasing. Bi-polar (windows) triggering mode was used and the sampling period was set as same length as the welding time in order to prevent signal leakage at the first welding cycle.
Carbon steel (AISI 1023) with 1.0 mm thickness metal sheets were used. As shown in Figure 4(a), the di-

Figure 3. Experimental setup of (a) signals measurement; (b) DAQ system.
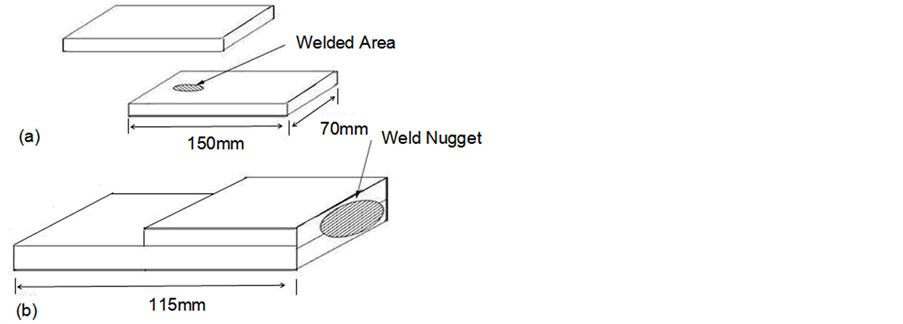
Figure 4. (a) SEM and (b) cross-sectional microscopic view of weld nugget.
mensions of metal sheet were obtained by using laser cutting to achieve good surface flatness and edge finishing. Furthermore, these metal sheets were rinsed by ethanol to remove contaminants such as oil, grease and etc. from the surface. The over-lapped area for the sheets is maintained at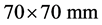 .
.
RWMA Class “A” standard was followed and a pair of C-type, cone tip Chromium Copper electrodes was used in the experiments. The electrode force and water flow rate was set at 2250 N and 2.5 litres per minute. In order to investigate the weld nugget growth with respect to different welding time, the SEM graphs of faying interface at the center of welded area were taken at the welding time, 0.02 s, 0.04 s and 0.06 s. On the other hand, the cross-sectional macroscopic graphs of the weld nugget along its centerline were taken at 0.04 s and 0.08 s (see Figure 4(b)).
3. Measurement of 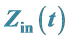
As shown in Figure 5 and Figure 6, the voltage and current signal based on 8.8 kA root mean square (RMS) welding current are presented. Basically, all the welding current presented in this paper is in RMS value. In order to obtain the analytic voltage and current signal, the Hilbert transform of both signals was calculated. As mentioned above, the product of Hilbert transform is to shift the original real-valued signal by +90˚ and then form the imaginary part of analytic signal. After taking the quotient of analytic voltage to current signal, the 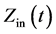 was calculated and presented in Figure 7. To illustrate the relationship between the
was calculated and presented in Figure 7. To illustrate the relationship between the 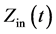 with weld
with weld
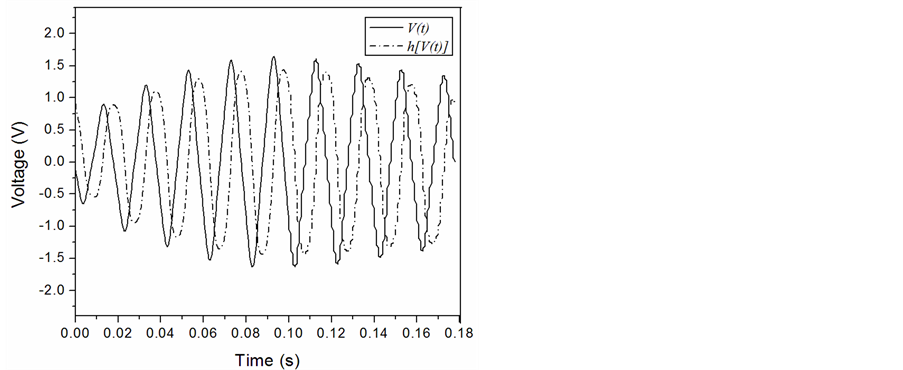
Figure 5. Welding voltage and its product of Hilbert transform.

Figure 6. Welding current and its product of Hilbert transform.
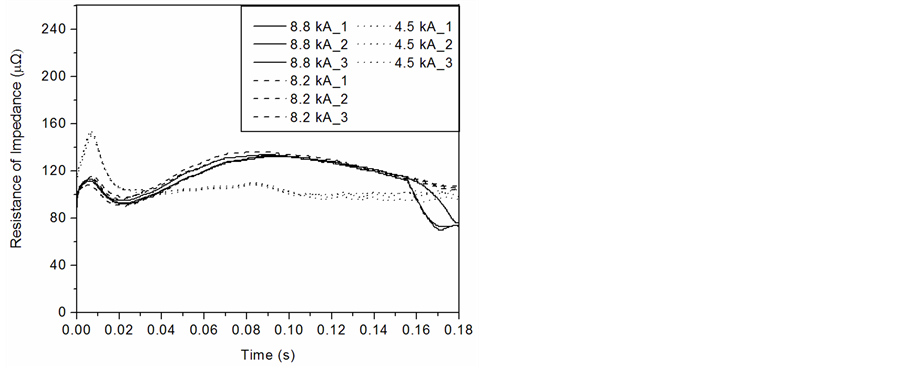
Figure 7. Time varying Zr(t) curves at different welding currents.
ing current, the 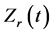 curves based on 4.5 kA, 8.2 kA and 8.8 kA welding current are presented. We observe that the
curves based on 4.5 kA, 8.2 kA and 8.8 kA welding current are presented. We observe that the 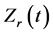 increases sharply and reaches the first peak before 0.01 s. After that, it decreases rapidly and the decrement stops at 0.02 s. For 8.2 kA and 8.8 kA welding current, the
increases sharply and reaches the first peak before 0.01 s. After that, it decreases rapidly and the decrement stops at 0.02 s. For 8.2 kA and 8.8 kA welding current, the 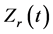 increases gently to the second peak at 0.10 s. However, the
increases gently to the second peak at 0.10 s. However, the 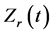 drops sharply in case of 8.8 kA welding current due to weld expulsion. On the other hand, no second peak appears for 4.5 kA welding current because “no weld” (no weld nugget) is made. In the followings, the time variation of
drops sharply in case of 8.8 kA welding current due to weld expulsion. On the other hand, no second peak appears for 4.5 kA welding current because “no weld” (no weld nugget) is made. In the followings, the time variation of  for 8.2 kA welding current is evaluated by comparing with the conventional dynamic contact resistance.
for 8.2 kA welding current is evaluated by comparing with the conventional dynamic contact resistance.
4. Evaluation of 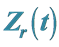
At the beginning of weld, the  increases rapidly from 90 μΩ to 112 μΩ because the contact resistance at faying interface is high. Due to the continuous heating, the
increases rapidly from 90 μΩ to 112 μΩ because the contact resistance at faying interface is high. Due to the continuous heating, the 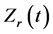 reaches the first peak when the contact resistance is at its maximum value at 0.01 s. By comparing with the dynamic contact resistance (as shown in Figure 2) and other researchers’ work [15] [16] , this first peak is present right at the beginning of weld. However, based on our finding and the experimental result obtained by Tan et al., the first peak of resistance should not be present at the beginning of weld. The incorrect location of the first peak could be caused by the rough measurement of dynamic contact resistance, which only considers the instant voltage and current at its peak value within every half cycle. Subsequently, the dynamic contact resistance has to lose the information at the beginning of weld since the quotient of voltage to current cannot be done when the voltage is zero. Furthermore, the dynamic contact resistance curve proposed by Dickinson et al. did not include the effect of contact electrical resistivity at the faying interface which has been proven to be important at the beginning of weld stage.
reaches the first peak when the contact resistance is at its maximum value at 0.01 s. By comparing with the dynamic contact resistance (as shown in Figure 2) and other researchers’ work [15] [16] , this first peak is present right at the beginning of weld. However, based on our finding and the experimental result obtained by Tan et al., the first peak of resistance should not be present at the beginning of weld. The incorrect location of the first peak could be caused by the rough measurement of dynamic contact resistance, which only considers the instant voltage and current at its peak value within every half cycle. Subsequently, the dynamic contact resistance has to lose the information at the beginning of weld since the quotient of voltage to current cannot be done when the voltage is zero. Furthermore, the dynamic contact resistance curve proposed by Dickinson et al. did not include the effect of contact electrical resistivity at the faying interface which has been proven to be important at the beginning of weld stage.
After the first peak, the 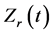 drops to 93 μΩ at 0.02 s. This significant drop in resistance is because the contact resistance is reduced to zero where the metal sheets are in intimate contact. As shown in Figure 8(a), some localized dents are found at the beginning of weld even though the metal sheets are assumed to be in intimate contact. However, these localized dents disappear and only dark color regions (recognized as burnt marks) are observed as result of softened metal sheets at high temperature after the welding process is started (see Figure 8(b)). Therefore, the metal sheets are truly in intimate contact and the contact resistance vanishes. Similarly, the same observation was reported by Tan et al.
drops to 93 μΩ at 0.02 s. This significant drop in resistance is because the contact resistance is reduced to zero where the metal sheets are in intimate contact. As shown in Figure 8(a), some localized dents are found at the beginning of weld even though the metal sheets are assumed to be in intimate contact. However, these localized dents disappear and only dark color regions (recognized as burnt marks) are observed as result of softened metal sheets at high temperature after the welding process is started (see Figure 8(b)). Therefore, the metal sheets are truly in intimate contact and the contact resistance vanishes. Similarly, the same observation was reported by Tan et al.
As shown in Figure 8(c) and Figure 8(d), the melting of metal starts at the faying interface from 0.04 s and 0.06 s due to the continuous heating of metal sheets. It reveals that the melting of metal initially happens at the faying interface where the contact resistance is high. As the metal sheets are continuously heated and reach its melting temperature, the melting of metal propagates vertically towards the upper and lower electrodes. This can be seen by the increment of  from 93 μΩ (at 0.02 s) to 133 μΩ (at 0.10 s).
from 93 μΩ (at 0.02 s) to 133 μΩ (at 0.10 s).
Figure 9 illustrates the history of weld nugget growth in correlation with the time variation of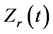 . Different welding time was set at 0.02 s, 0.04 s, 0.06 s, 0.08 s, 0.10 s, 0.12 s, 0.14 s, 0.16 s and 0.18 s in order to
. Different welding time was set at 0.02 s, 0.04 s, 0.06 s, 0.08 s, 0.10 s, 0.12 s, 0.14 s, 0.16 s and 0.18 s in order to

Figure 8. SEM graphs of faying interface at the center of welded area, welding time = (a) 0 s; (b) 0.02 s; (c) 0.04 s; (d) 0.06 s.
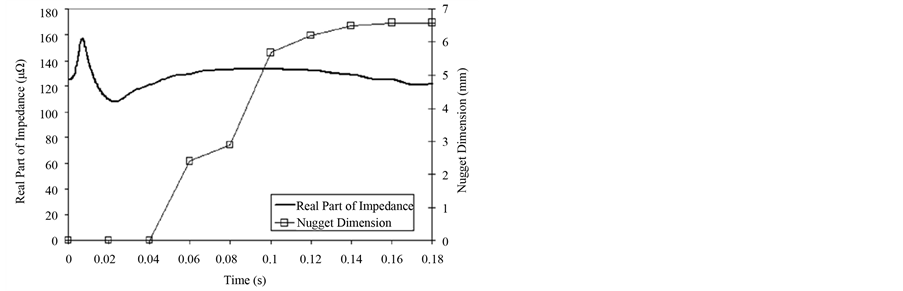
Figure 9. Relationship between the weld nugget growth and Zr(t) curve along welding time.
make the spot welds at the specified instant moment. After the spot welds were done based the aforementioned welding times, the diameter of weld nuggets was measured according to the BS standard [17] . Firstly, the top plate of spot weld was torn away before the measurement. Two diagonal diameters of weld nugget was measured and then averaged to obtain the final value of weld nugget diameter. It is found that the weld nugget starts to grow in between 0.04 s to 0.06 s. From 0.10 s onwards, the size of weld nugget does not change significantly until the end of welding process. In fact, good agreement is found when examining the time variations of . Therefore, this observation suggests that the
. Therefore, this observation suggests that the 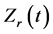 can be used for the characterization of weld nugget growth.
can be used for the characterization of weld nugget growth.
5. In-Process Characterizing of Weld Nugget Growth
In order to demonstrate the characterization of in-process weld nugget growth, the  based on the spot weld at 8.8 kA welding current is divided into 5 stages (as shown in Figure 10): (I) initial heating; (II) contact resistance breakdown; (III) bulk heating; (IV) weld nugget growing and (IV) end of welding and expulsion. In the followings, each stage will be discussed and compared with the findings from Tan et al. and dynamic contact resistance to confirm the correlations between the features of
based on the spot weld at 8.8 kA welding current is divided into 5 stages (as shown in Figure 10): (I) initial heating; (II) contact resistance breakdown; (III) bulk heating; (IV) weld nugget growing and (IV) end of welding and expulsion. In the followings, each stage will be discussed and compared with the findings from Tan et al. and dynamic contact resistance to confirm the correlations between the features of 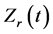 with the weld nugget growth.
with the weld nugget growth.
Stage I. At 0 s, the contact resistance is usually unstable because it is mainly depended on the contact conditions at the faying interface. As shown in Figure 8(a), the metal sheets are not in full contact due to the presence of localized dents with air, which the resistivity of air is considered extremely high. Therefore, the 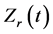 increases rapidly to the alpha peak at 0.01 s.
increases rapidly to the alpha peak at 0.01 s.
As shown in Figure 2, this alpha peak is not seen from the dynamic contact resistance reported by Dickinson

Figure 10. 5 stages of Zr(t) curve.
et al. In fact, there were no reports to reveal this phenomenon until the joining of thin Ni sheets done by DC RSW was carried out and reported by Tan et al. Since DC current was used, it is possible to obtain the alpha peak because the time-varying resistance curve is easily calculated based on Ohm’s Law. Given the possible reasons for having no alpha peak, it could be due to extremely high increasing rate of current and the presence of thick surface film at the faying interface. However, both possibilities are not true based on our findings. Firstly, the increasing rate of current for large scale RSW is much higher as compared to small scale RSW. For an example, the increasing rate of current for 8.8 kA welding current is rated at 147,000 A/s based on an average ramp-up time of 60 ms. Despite of having such a high increasing rate, the alpha peak still appears in the 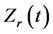 curve. On the other hand, the surface of metal sheets used in the experiments was not mechanically treated. It means that a thin layer of oxide film is present during the welding process. In other words, the alpha peak can be identified easily by the proposed method.
curve. On the other hand, the surface of metal sheets used in the experiments was not mechanically treated. It means that a thin layer of oxide film is present during the welding process. In other words, the alpha peak can be identified easily by the proposed method.
Stage II. The  drops sharply to a lower value where the “trough” is defined. As mentioned earlier, the metal sheets are softened and deformed so that there are no more gaps at the faying interface. Therefore, only bulk resistance is obtained at the trough and the contact resistance at the faying interface is zero.
drops sharply to a lower value where the “trough” is defined. As mentioned earlier, the metal sheets are softened and deformed so that there are no more gaps at the faying interface. Therefore, only bulk resistance is obtained at the trough and the contact resistance at the faying interface is zero.
Stage III. The bulk resistance increases as the temperature of metal sheets is increasing. Without the abruptly change of contact resistance, the 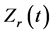 is able to increase gently. Local melting at the faying interface is observed at 0.02 s and the heating of metal sheets is still continuous. Therefore, we should define this stage as “bulk heating” only which is not clearly shown in the dynamic contact resistance.
is able to increase gently. Local melting at the faying interface is observed at 0.02 s and the heating of metal sheets is still continuous. Therefore, we should define this stage as “bulk heating” only which is not clearly shown in the dynamic contact resistance.
Stage IV. This is the most important stage because it shows the formation of weld nugget. As shown in Figure 11(a) and Figure 11(b), the weld nugget starts to form from the faying interface and fully develop to its final shape. Basically, the cooling water in the electrode removes the excessive heat from the metal sheets. Therefore, it cools down the electrodes and the outer surface of metal sheets so that the molten metal will not penetrate out the enclosure of liquid weld nugget. During this stage, the  reaches the beta peak (133 μΩ) where the size of weld nugget is confirmed. After 0.10 s, the
reaches the beta peak (133 μΩ) where the size of weld nugget is confirmed. After 0.10 s, the  reduces gently from the beta peak to 127 μΩ because of the indentation of electrodes resulting in decreasing of the bulk resistance after the metal sheets are softened. In case of “no weld”, it is expected to have no beta peak (as shown in Figure 7 for welding current 4.5 kA) because no weld nugget is formed eventually.
reduces gently from the beta peak to 127 μΩ because of the indentation of electrodes resulting in decreasing of the bulk resistance after the metal sheets are softened. In case of “no weld”, it is expected to have no beta peak (as shown in Figure 7 for welding current 4.5 kA) because no weld nugget is formed eventually.
Stage V. The 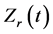 reduces abruptly at 0.16 s which is defined as “Cliff”. Due to the weld expulsion, the molten metal is ejected from the weld nugget at the faying interface. Therefore, it causes very serious indentation of electrode which results into a shorter electrical path and then lower resistance. According to the observations from the results, the higher amplitude of “cliff” is measured, the more severe weld expulsion can be.
reduces abruptly at 0.16 s which is defined as “Cliff”. Due to the weld expulsion, the molten metal is ejected from the weld nugget at the faying interface. Therefore, it causes very serious indentation of electrode which results into a shorter electrical path and then lower resistance. According to the observations from the results, the higher amplitude of “cliff” is measured, the more severe weld expulsion can be.
6. Conclusions
In this paper, the time varying 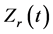 of input electrical impedance was discussed by comparing with the dynamic contact resistance curve as reported in the literatures. It showed that the proposed method is capable to obtain an accurate and time-varying resistance because the
of input electrical impedance was discussed by comparing with the dynamic contact resistance curve as reported in the literatures. It showed that the proposed method is capable to obtain an accurate and time-varying resistance because the  is inherently isolated from the influence of inductive noise which is only reflected by the
is inherently isolated from the influence of inductive noise which is only reflected by the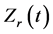 . Furthermore, the measurement of
. Furthermore, the measurement of 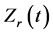 is done by tap-
is done by tap-

Figure 11. Microscopic view of weld nugget, welding time = (a) 0.04 s; (b) 0.08 s.
ing the current and voltage probe on the electrodes of welding machine without jeopardizing the normal welding operations. Therefore, it is an accurate, easy-to-use, robust and cost effective method to investigate the inprocess changes of weld nugget growth.
After the investigation was done on a typical spot weld with weld expulsion, several important findings were concluded as followed:
A new characteristic curve based on the 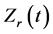 of input electrical impedance was established. Several feature points of
of input electrical impedance was established. Several feature points of 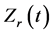 were identified to characterize the in-process changes of weld nugget growth.
were identified to characterize the in-process changes of weld nugget growth.
The “alpha peak” can be identified easily from the 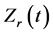 curve despite of reasons given by Tan et al., 1) extremely high increasing rate of current; 2) the presence of thick surface film at the faying interface.
curve despite of reasons given by Tan et al., 1) extremely high increasing rate of current; 2) the presence of thick surface film at the faying interface.
Based on the 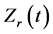 curve, a new stage “(III) bulk heating” has been identified clearly to better reflect the change of temperature during welding process.
curve, a new stage “(III) bulk heating” has been identified clearly to better reflect the change of temperature during welding process.
Since the 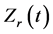 curve is truly time varying, it is possible to determine the instantaneous temperature of welding process based on the
curve is truly time varying, it is possible to determine the instantaneous temperature of welding process based on the 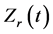 curve because the resistance is proportional to the resistivity of metal sheets and air gap which is sensitive to the change of temperature.
curve because the resistance is proportional to the resistivity of metal sheets and air gap which is sensitive to the change of temperature.
Acknowledgements
The authors thank Dr. Tan Tong Tat for his kind supports and valuable comments of this manuscript.
References
- Scharff, R. and Caruso, D. (1990) Complete Automotive Welding Metals and Plastics. Albany, New York.
- Harlin, N., Jones, T.B. and Parker, J.D. (2003) Weld Growth Mechanism of Resistance Spot Welds in Zinc Coated Steel. Journal of Material Processing Technology, 143-144, 448-453.http://dx.doi.org/10.1016/S0924-0136(03)00447-3
- Dickinson, D.W., Franklin, J.E. and Stanya, A. (1980) Characterization of Spot Welding Behavior by Dynamic Electrical Parameter Monitoring. Welding Journal, 59, 170-176.
- Gedeon, S.A., Sorensen, C.D., Ulrich, K.T. and Eagar, T.W. (1987) Measurement of Dynamic Electrical and Mechanical Properties of Resistance Spot Welds. Welding Journal, 66, 378-385.
- Cho, Y. and Rhee, S. (2002) Primary Circuit Dynamic Resistance Monitoring and Its Application to Quality Estimation during Resistance Spot Welding. Welding Journal, 81, 104-111.
- Wang, S.C. and Wei, P.S. (2001) Modeling Dynamic Electrical Resistance during Resistance Spot Welding. Transactions of the ASME, Journal of Heat Transfer, 123, 576-585. http://dx.doi.org/10.1115/1.1370502
- Garza, F. and Das, M. (2001) On Real Time Monitoring and Control of Resistance Spot Welds Using Dynamic Resistance Signatures. Proceeding of the 44th IEEE-Midwest Symposium on Circuits and Systems, Dayton, 14-17 August 2001, 41-44.
- Tan, W., Zhou, Y., Kerr, W. and Lawson, S. (2004) A Study of Dynamic Resistance during Small Scale Resistance Spot Welding of Thin Ni Sheets. Journal of Physics D: Applied Physics, 37, 1998-2008.http://dx.doi.org/10.1088/0022-3727/37/14/017
- Ling, S.-F., Luan, J., Li, X.C. and Ang, W.L.Y. (2006) Input Electrical Impedance as Signature for Nondestructive Evaluation of Weld Quality during Ultrasonic Welding of Plastics. NDT & E International, 39, 13-18.http://dx.doi.org/10.1016/j.ndteint.2005.05.003
- Ling, S.-F., Zhang, D., Yi, S. and Foo, S.W. (2006) Real-Time Quality Evaluation of Wire Bonding Using Input Impedance. IEEE Transactions on Electronics Packaging Manufacturing, 29, 280-284.http://dx.doi.org/10.1109/TEPM.2006.887400
- Fu, L.Y., Ling, S.-F. and Tseng, C.-H. (2007) On-Line Breakage Monitoring of Small Drills with Input Impedance of Driving Motor. Mechanical Systems and Signal Processing, 21, 457-465.http://dx.doi.org/10.1016/j.ymssp.2005.04.004
- Ling, S.-F., Wan, L.-X., Wong, Y.-R. and Li, D.-N. (2010) Input Electrical Impedance as Quality Monitoring Signature for Resistance Spot Welding. NDT & E International, 43, 200-205. http://dx.doi.org/10.1016/j.ndteint.2009.11.003
- Julius, S.B. and Allan, P.G. (2000) Random Data: Analysis and Measurement Procedures. 3rd Edition, Wiley, New York, 518-543.
- Boctor, S.A. and David, A.B. (1992) Electrical Circuit Principles. Prentice Hall Inc., Englewood Cliffs, 489-536.
- Cho, Y. and Rhee, S. (2000) New Technology for Measuring Dynamic Resistance and Estimating Strength in Resistance Spot Welding. Measurement Science & Technology, 11, 1173-1178.http://dx.doi.org/10.1088/0957-0233/11/8/311
- Chen, J.Z. and Farson, D.F. (2006) Analytical Modeling of Heat Conduction for Small Scale Resistance Spot Welding Process. Journal of Material Processing Technology, 178, 251-258. http://dx.doi.org/10.1016/j.jmatprotec.2006.03.175
- BS 1140:1993 (1993) Specification for Resistance Spot Welding of Uncoated and Coated Low Carbon Steel. BSI Publications, London.
NOTES

*Corresponding author.

