Engineering
Vol.5 No.10(2013), Article ID:36744,11 pages DOI:10.4236/eng.2013.510095
An Experimental Study on the Effect of Foundation Depth, Size and Shape on Subgrade Reaction of Cohessionless Soil
Faculty of Engineering, Sinai University, El Arish, Egypt
Email: wael_nashaat74@yahoo.com
Copyright © 2013 Wael N. Abd Elsamee. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 29, 2013; revised July 29, 2013; accepted August 7, 2013
Keywords: Subgrade Reaction; Plate Load Test; Foundation Depth; Size; Shape
ABSTRACT
The modulus of subgrade reaction ks depends on several factors such as the size and shape of the foundation as well as the embedment depth of the foundation. The present study is an experimental analysis using plate load test to determine the effect of foundation depth, size as well as the shape on the modulus of subgrade reaction (ks) of cohesionless soils. It was carried out by using nine rigid steel plates with different sizes and shapes (circular, square and rectangular). The tests were carried out on cohessionless soil with different relative densities under different applied pressures. The settlement has been measured at the surface of the plate for different depths of footings. The ultimate bearing capacity [qu] has been determined from the stress-settlement relationships. The allowable bearing capacity (qa) was determined by dividing the ultimate bearing capacity (qu) by F.S. = 3.0, after which the corresponding settlement (Sa) has been obtained. However, ks was calculated based on dividing the allowable bearing capacity (qa) by the corresponding settlement (Sa). From the present study it is concluded that the subgrade reaction ks of cohessionless soil increases with increasing foundation depth as well as foundation size. In addition, subgrade reaction ks of cohessionless soil under rectangular footing is higher than that under square and that under circular one with same equivalent area. An empirical formula is presented to calculate the subgrade reaction ks of cohessionless soil under square foundation taking into consideration foundation depth. Fair agreement has been obtained between values of ks from the empirical formula at depth of footing = 0.00 B and Biot (1937) as well as Meyerhof and Baike (1965).
1. Introduction
Soil bearing capacity and soil modulus of subgrade reaction are some various measures of strength-deformation properties of soil. To perform the structural analysis of footings one must know the principles of evaluating the coefficient of subgrade reaction “ks”.
One of the most popular models in determining the modulus of subgrade reaction is Winkler (1867) model [1]. In this model the subgrade soil is assumed to behave like infinite number of linear elastic springs that the stiffness of the spring is named as the modulus of subgrade reaction. This modulus depends on some parameters such as soil type, size, shape, depth and type of foundation.
Iancu-B. T. and Ionut O. T. (2009) presented a numerical simulation of plate loading test in order to underlines the size effect on settlements. The obtained results are compared with Finite Element Method (FEM) using the Mohr-Coulomb soil model. The obtained numerical results revealed that the subgrade reaction coefficient was strictly dependent on the size of the loaded area and the loading magnitude [2].
Elsamny, M. K., Elsedeek, M. B. and Abd Elsamee, W. N. (2010) presented field determination of the Young’s modulus “Es” of footings on cohesionless soil by using plate load test [3].
Dae. S. K. and Seong Y. P. (2011) presented plate loading tests to evaluate the compaction quality of the railroad subgrade in Korea. Two methods to determine the design modulus were used. One is an unrepetitive plate loading test (uPLT) that obtains the subgrade reaction modulus (K30) and the other is a repetitive plate loading test (rPLT) that obtains the strain modulus (Ev) [4].
Aminaton M. et al. (2012) presented Winkler model and the sub grade soil is assumed to behave like infinite number of linear elastic springs. The foundation size effect on sandy sub grade by using of finite element software (Plaxis) is presented [5].
2. Determination of Subgrade Reaction “ks”
2.1. Determination of Subgrade Reaction “ks” Using the Elastic Parameters “Es, vs”
The coefficient of subgrade reaction ks is the ratio between the pressure “q” at any given point and the settlement “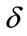 ” produced by load application at that point.
” produced by load application at that point.
Biot (1937), Terzaghi (1955), Vesic (1961), Meyerhof and Baike (1965), Selvadurai (1984) and Bowles (1998) have investigated the factors affect the determination of ks. Biot (1937) solved the problem for an infinite beam with a concentrated load resting on a 3D elastic soil continuum. Biot found a correlation of the continuum elastic theory and Winkler model [6]. Vesic (1961) tried to develop a value for ks, by matching the maximum displacement of the beam. He obtained an equation for ks to be used in the Winkler model [7,8].
However, different formulii to calculate the modulus of subgrade reaction “ks” by some different authors are presented in Table 1.
2.2. Determination of Subgrade Reaction “ks” in-Situ Using Plate Loading Test (P.L.T)
The plate-load test provides a direct measure of compressibility and occasionally of the bearing capacity of soils which are not easily sampled. The modulus of subgrade reaction can be determined by using the plate-load test as follows:
2.2.1. Terzaghi’s Method (1955)
A major problem is to estimate the numerical value of “ks”. One of the early contributions was that of Terzaghi (1955) [9]. He suggested values of ks for (1 × 1) ft rigid slab placed on a soil medium. “ksf” for full-sized footings could be obtained from plate-load tests using the following equations:
1) For square footing on cohesionless soil with dimensions = B × B.
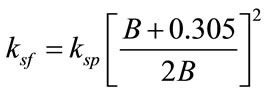 (1)
(1)
2) For rectangular footing on cohesionless soil with dimensions = B × L.
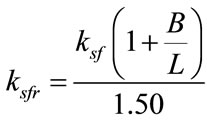 (2)
(2)
3) For long foundation [strip footing] with a width = B The modulus of subgrade reaction is approximately equal to 0.67 ksf
where:

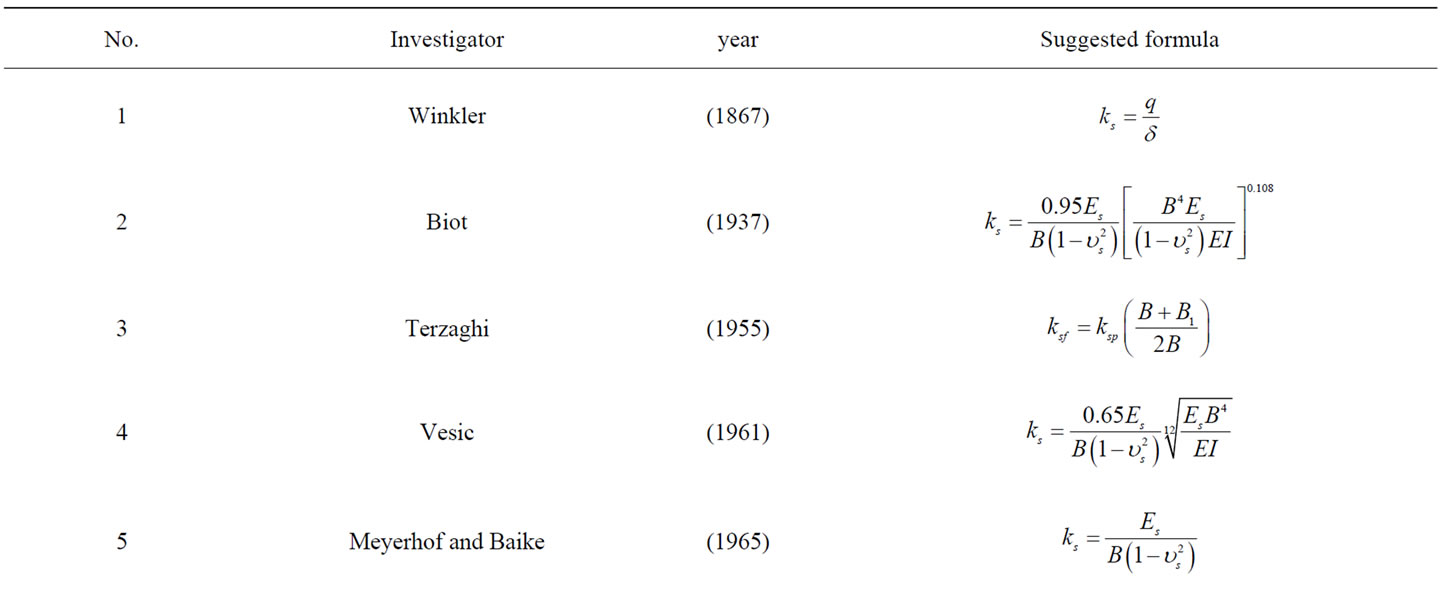
Table 1. Some different formulii to calculate the modulus of subgrade reaction, ks.
ksp = plate-load test value of modulus of subgrade reaction kN/m3, using square plate (1 × 1) ft or circular plate with diameter = 0.305 m;
ksf = desired value of modulus of subgrade reaction for full-sized square footings B × B, kN/m3;
ksfr= desired value of modulus of subgrade reaction for rectangular full-sized footings B × L, kN/m3;
B = footing width, meter or least dimension of rectangular or strip.
2.2.2. Different Cods
American Code (ASTM D1194) (1994) and British standards Code (BS5930) (1997):
American Code (ASTM D1194) (1994) and British standards Code (BS5930) (1997) estimated the numerical value of “ks” from plate load test results [10].
2.2.3. Peck, Hanson and Thobrnburn (1997)
Peck, Hanson and Thobrnburn (1997) estimated the numerical value of “ks” by using plate load test as fol- lows:
1) Settlement on sands occurs almost entirely during construction.
2) Maximum differential settlement between footings on sand is less than 20 mm.
3) “ks” is calculated from the straight line portion of the load-settlement curve.
2.2.4. Ping-Sien Lin, Li-Wen Yang and C. Hsein Juang (1998)
Ping-Sien Lin, Li-Wen Yang and C. Hsein Juang (1998) made a series of plate-load tests to investigate the load settlement characteristics of a gravelly cobble deposit and estimate the value of modulus of subgrade reaction “ks” as follows:
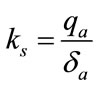 (3)
(3)
where:
ks = modulus of subgrade reaction, kN/m3;
qa = allowable bearing capacity, kN/m2;
da = allowable settlement against q = qa, meter
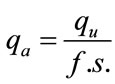 (4)
(4)
where:
qu = Ultimate bearing capacity, kN/m2;
f.s. = Factor of safety = 3 [11].
2.2.5. Egyptian Code (2001)
Egyptian Code (2001) made a series of plate-load tests to investigate the load settlement characteristics and estimates the value of modulus of subgrade reaction “ks” as follows:
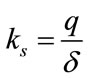 (5)
(5)
where:
ks = Modulus of subgrade reaction, (kN/m3);
q = Stress at settlement =1.3 mm after ten times loaded, (kN/m2);
d = Settlement against q (meter) [12].
2.2.6. Reza Z. M. and Masoud J. (2008)
Reza Z. M. and Masoud J. (2008) presented a direct method to estimate the modulus of subgrade reaction by the plate load test done with 30 - 100 cm diameter circular plate or equivalent rectangular plate [13].
However, Table 2 presents some different methods using plate load test with different sizes and shapes to determinate the value of modulus of subgrade reaction, ks.
3. Present Experimental Study
Plate load tests have been carried out in field and the settlement of sandy soil was measured under different stress levels. In the present study each sample has been placed in an open box and compacted in layers with different relative densities. Settlement has been measured under different stresses and at different relative densities as well as different depth of foundations.
3.1. Field Samples
Graded sand (GS) at different relative densities was used in field. Each sample has been compacted in layer and the relative density for each layer has been determined by using sand cone.
3.2. Loading
The load has been applied by using steel frame fixed in the ground as shown in Figure 1. The applied load has been measured by using pressure gauge connected to a jack.
3.3. Used Plates
Nine steel rigid plates were used in the tests which are divided into three groups. The first group has rigid three circular shape plates. The second group is three rigid square plates first one having dimension (1 * 1) ft and the other two square plates having equivalent area for 455 mm and 610 diameter. The last group is a rigid three rectangular plate having the same equivalent areas as the first group. The plates have concentric marking on one face and plated against corrosion. The plates have a finished thickness of 32 mm and are according to ASTM D1194 and D1196 specification as shown in Table 3 and Figure 2.
3.4. Depth of Foundations
The settlement has been measured at surface and at different depths. The depth of foundation is considered a function of width of the plate B. Circular, square and rectangular steel boxes have been placed around the rigid steel plates to be used in case of filling soil around as surcharge for different foundation depths (0.25 B, 0.50 B, 0.75 B and 1.00 B).
3.5. Test Procedure
The test procedure is as follows:
1) The soil has been placed in a square open box.
2) The box was filled with different soil layers compacted to different densities which has been determined by sand cone test. The field compaction has been done
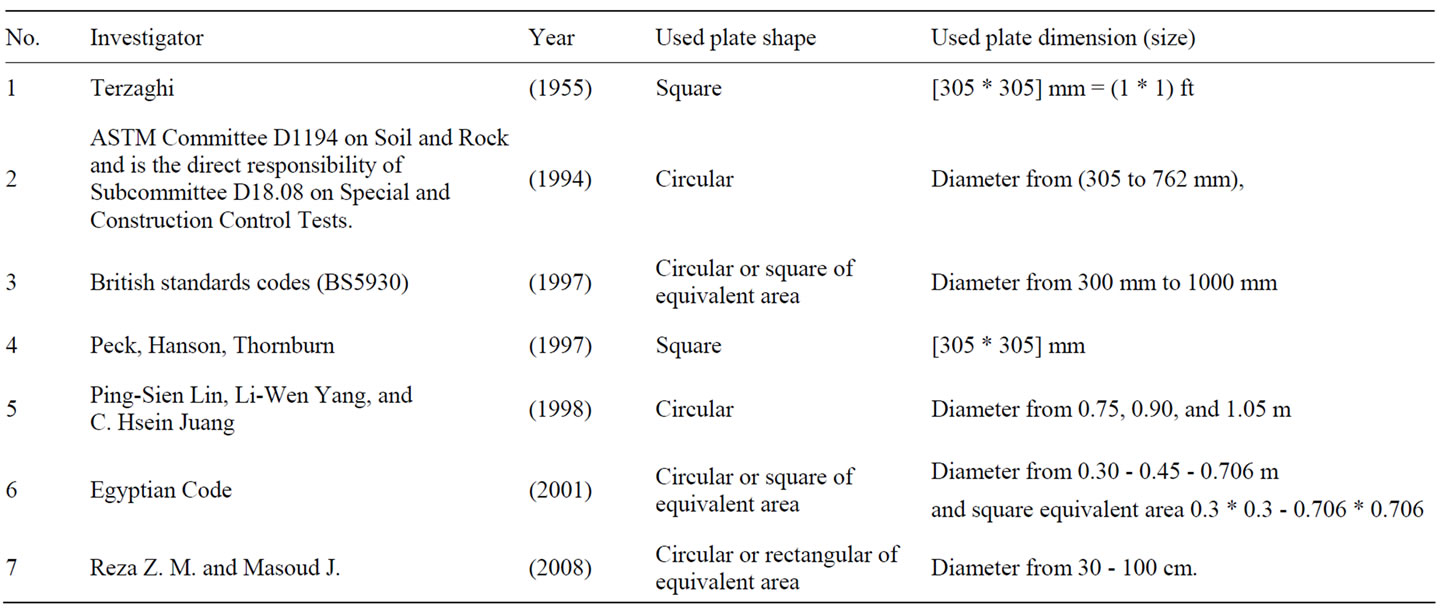
Table 2. Some different methods using plate load test to calculate ks.

Table 3. The used plates in the experimental study.

Figure 1. Loading frame.

Figure 2. The nine rigid plates.
using the following:
a) Each compacted layer has (7.5) cm thick ness.
b) A (4.5) kg weight hammer was used and released from (30) cm height.
3) The surface of the tested soil was prepared for plate test using fine sand at the surface.
4) The steel plates were placed on the prepared surface.
5) A hydraulic jack was placed on the steel plate.
6) Four dial gauges has been placed on the plate surface.
7) The settlement has been measured by using dial gauges of sensitivity 0.01 mm placed on the edges of the steel plate. Figure 3 shows measuring settlement at surface.
8) Steel boxes have been placed around the rigid steel plates to be used in case of filling soil around as surcharge for different foundation depths (0.25) B, (0.50) B and (1.00) B as shown in Figures 4 and 5.
9) The load was applied in increments by using steel frame. Each load increment was maintained constant until the settlement rate reaches 0.02 mm/min and not less than one hour in any case.
4. Experimental Results
Settlement in field was recorded for different footings

Figure 3. Settlement readings at surface using dial gauges.

Figure 4. Settlement readings in case of surcharge using circular steel box.

Figure 5. Settlement readings in case of surcharge using square steel box.
sizes and shapes (circular, square and rectangular) under different stresses ranging between 0.589 kN/m2 and 5.301 kN/m2. However, the settlement has been measured at different relative densities and at different depths (0.00 B), (0.25 B), (0.50 B), (0.75 B) and (1.00 B) for all kind of plates. From the measured settlement of cohessionless soil the following relationships are obtained.
4.1. Ultimate Bearing Capacity Using Experimental Results
The ultimate bearing capacity of cohessionless soil has been determined from the relationships between the stresses and the measured settlement at surface and at different depths for all plates by tangent-tangent method according Egyptian Code. Figure 6 gives an example of determination of the ultimate capacity.
4.2. Determination of Subgrade Reaction “ks” Using Experimental Results
The allowable bearing capacity (qa) is determined by dividing the ultimate bearing capacity (qu) by F.S. =3.0, after which the corresponding settlement (Sa) is determined. Thus, ks is calculated based on dividing the allowable bearing capacity (qa) by the corresponding settlement (Sa) as shown in Figure 7.
5. Effect of Foundations Depth on Subgrade Reaction “ks”
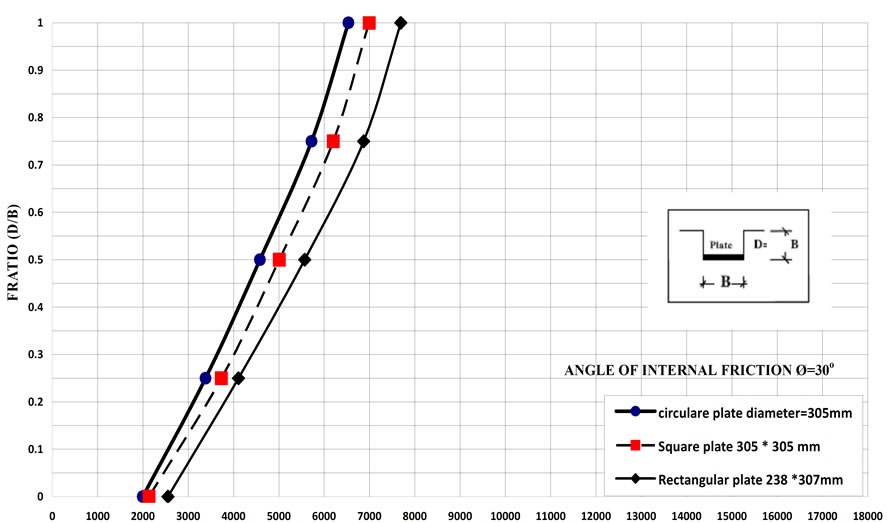
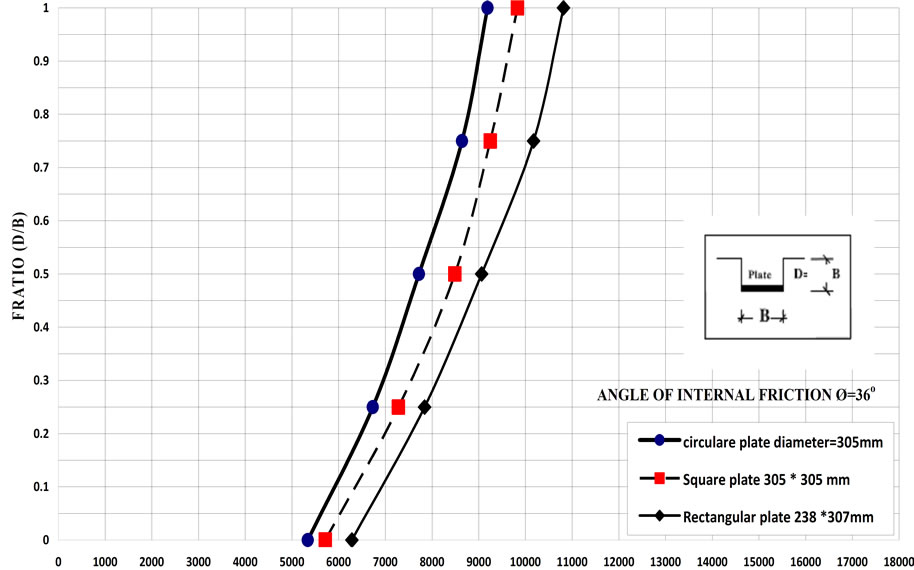
The effect of foundations depth on subgrade reaction ks has been investigated. However, the values of subgrade reaction ks have been obtained under different plates with different foundation depths as shown in Table 4. Figures 8 and 9 show examples for the effect of footing depth on ks for different angle of internal friction under different plate shapes. These figures show that subgrade reaction ks of cohessionless soil increases with increasing footing depth.
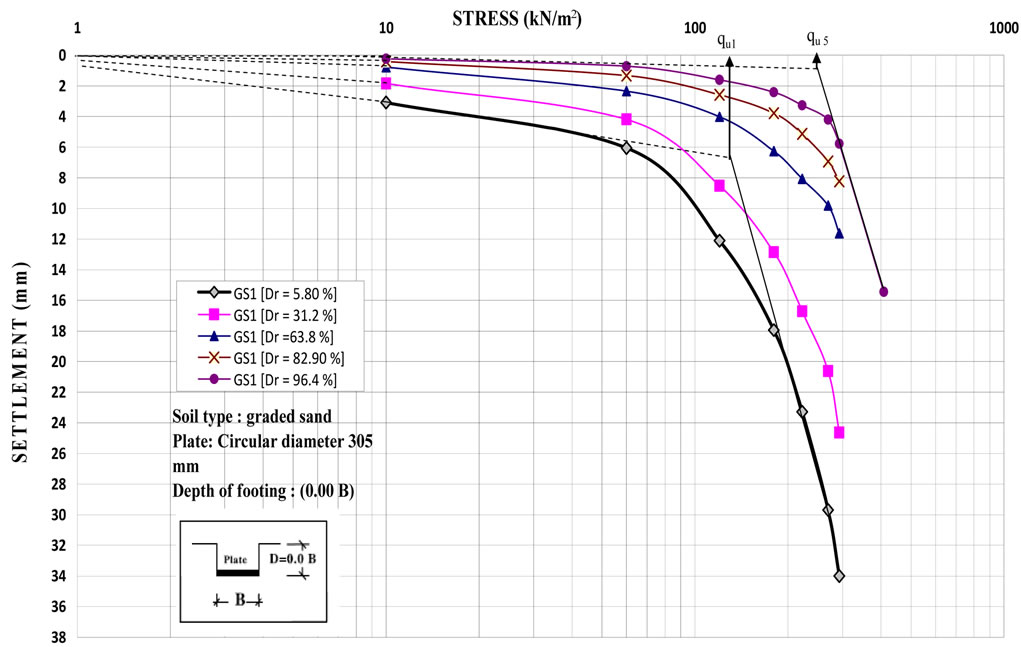
Figure 6. The relationship between stress and settlement of plate for determination of ultimate bearing capacity for circular plate diameter 355 mm.
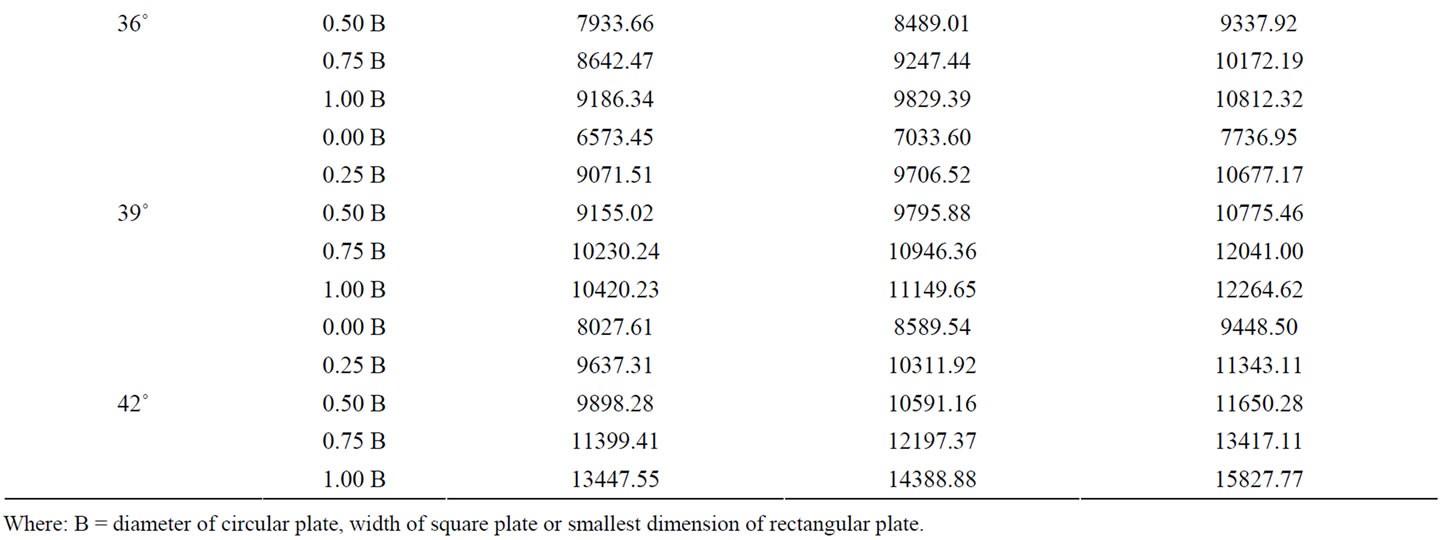

Table 4. Values of ks (kN/m3) of cohessionless soil using plate load test diameter 305 mm, square 305 * 305 mm (1 * 1) ft and rectangular 238 * 307 mm (equivalent area for 305 mm diameter).

Figure 7. Determination of subgrade reaction “ks”.
SUBGRADE REACTION Ks (kN/m3)
Figure 8. The relationship between subgrade reaction ks and depth of foundation for different shapes of footing for angle of internal friction ø = 30˚.
SUBGRADE REACTION Ks (kN/m3)
Figure 9. The relationship between subgrade reaction ks and depth of foundation for different shapes of footing for angle of internal friction ø = 36˚.
6. Effect of Foundations Size on Subgrade Reaction “ks”
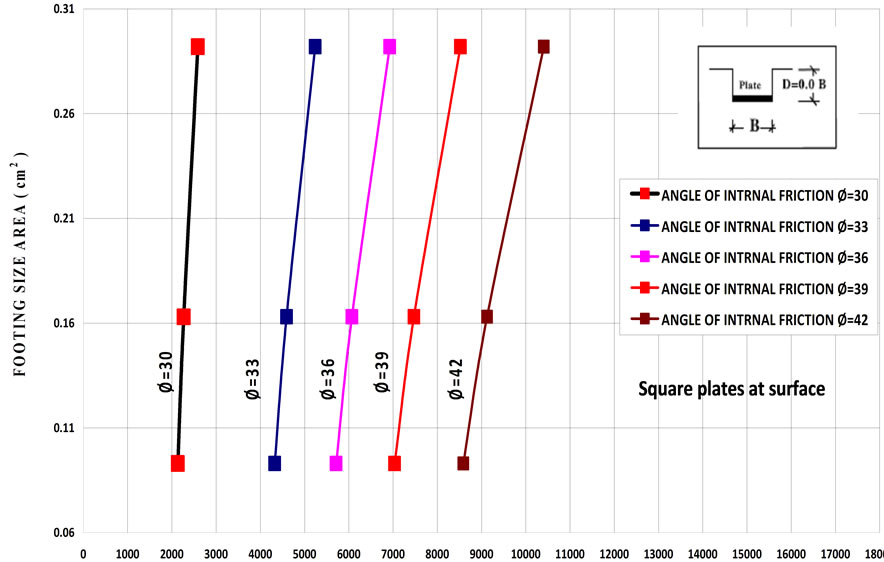
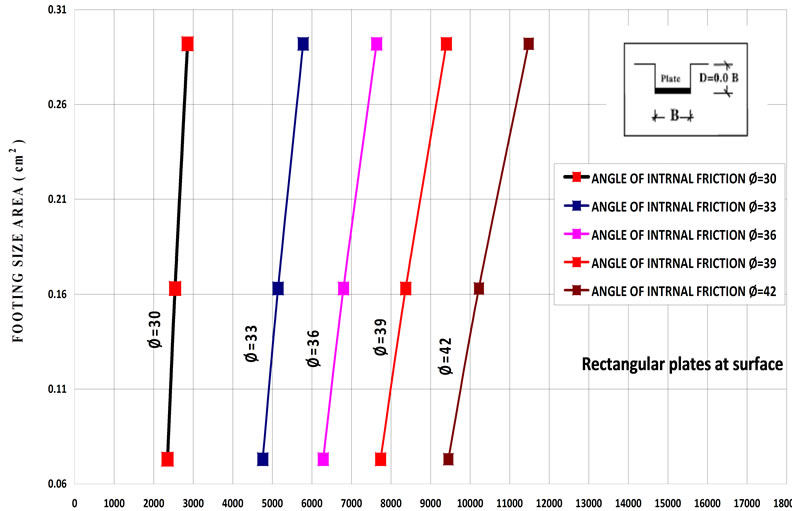
The relationship between subgrade reaction ks and footing sizes for different shapes of footing has been obtained. Figures 10-12 show examples for the effect of footing sizes on ks for different angle of internal friction. These figures show that subgrade reaction ks of cohessionless soil increases with increasing footing size for all type of foundations. In addition, subgrade reaction ks of cohessionless soil increases with increasing angle of internal friction.
7. Effect of Foundations Shape on Subgrade Reaction “ks”
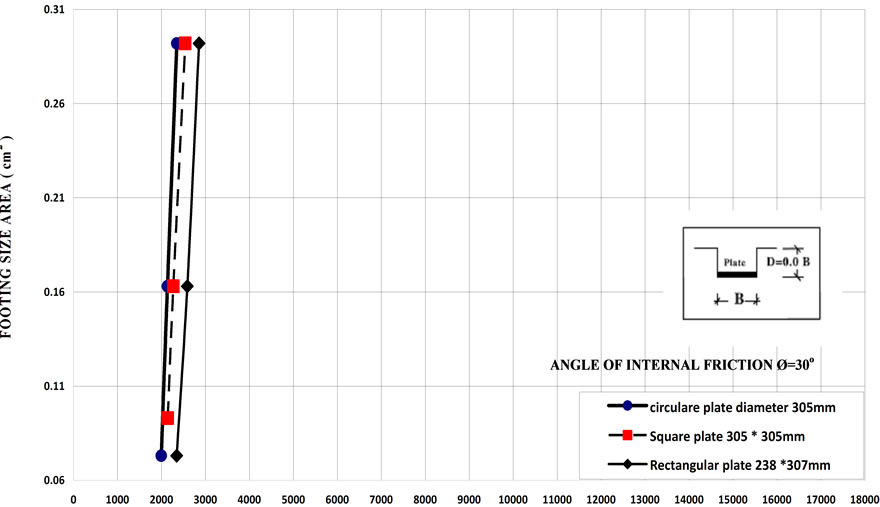
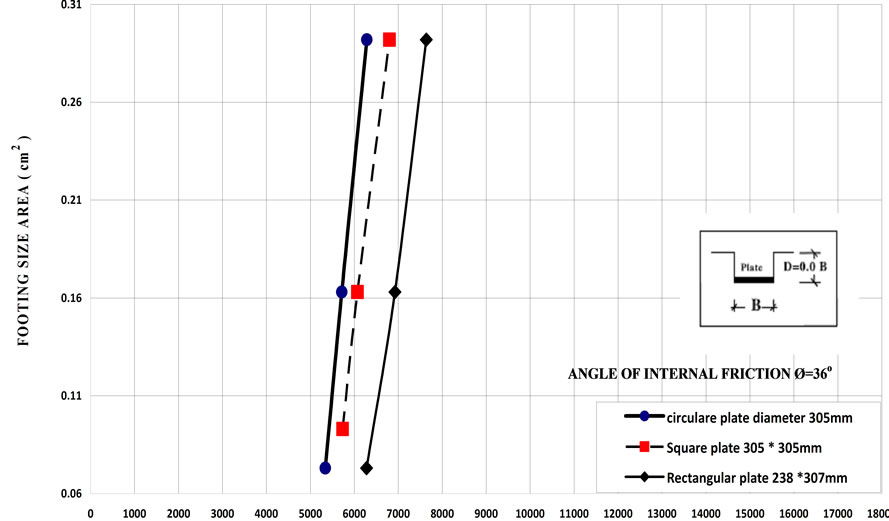
The values of subgrade reaction ks have been obtained for different plates under different foundation shapes for different depths. Figures 13-15 give examples for the effect of footing shapes on ks. From these fingers it can be shown that subgrade reaction ks of cohessionless soil under rectangular plate is higher than that under square than that under circular one (at same equivalent area).
8. The Obtained Values of “ks” for Cohessionless Soil
Tables 5 and 6 show the obtained value of ks for cohessionless soil.
9. Empirical Formula
A convergence study was performed to determine the subgrade reaction (ks) using “SPSS” statistical scientific

SUBGRADE REACTION Ks (kN/m3)
Figure 10. The relationship between subgrade reaction ks and footing sizes at surface for circular plates [size 305, 455 and 610 mm].
SUBGRADE REACTION Ks (kN/m3)
Figure 11. The relationship between subgrade reaction ks and footing sizes at surface for square plates [size equivalent area of 305, 455 and 610 mm].
SUBGRADE REACTION Ks (kN/m3)
Figure 12. The relationship between subgrade reaction ks and footing sizes at surface for rectangular plates [size equivalent area of 305, 455 and 610 mm].
SUBGRADE REACTION Ks (kN/m3)
Figure 13. The relationship between subgrade reaction ks and footing size at depth of footing B = 0 (at angle of internal friction ø = 30˚).
SUBGRADE REACTION Ks (kN/m3)
Figure 14. The relationship between subgrade reaction ks and footing size at depth of footing B = 0 (at angle of internal friction ø = 36˚).

SUBGRADE REACTION Ks (kN/m3)
Figure 15. The relationship between subgrade reaction ks and footing size at depth of footing B = 0 (at angle of internal friction ø = 42˚).
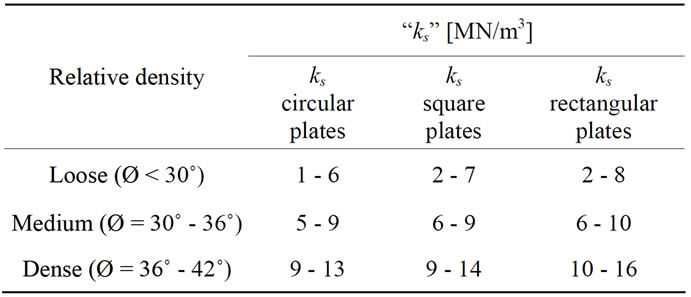
Table 5. The obtained values of “ks” for cohessionless soil [MN/m3] at depth of foundation = 0.00 B.
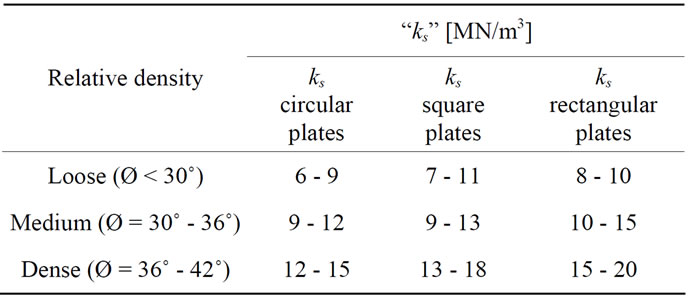
Table 6. The obtained values of “ks” for cohessionless soil [MN/m3] at depth of foundation = 1.00 B.
program. From the experimental analysis the following empirical formula is presented. The empirical formula is derived to calculate subgrade reaction (ks) for cohessionless soil under the square foundations using regression methods:
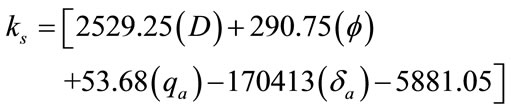 (6)
(6)
where:
ks = Modulus of subgrade reaction, (kN/m3);
Ø = angle of internal friction;
D = depth of foundation (meter);
qa = Allowable bearing capacity, (kN/m2);
da = Settlement at allowable bearing capacity (meter);
ks is dependant and D, Ø, qa, da are independent.
One-way analysis of variance (One-Way ANOVA) is used to calculate correlation coefficients of the resulting equation. The One-Way ANOVA procedure produces a one-way analysis of variance for a quantitative dependent variable by a single factor (independent) variable. Analysis of variance is used to test the hypothesis. This technique is an extension of the two-sample test. The number of cases, mean, and standard deviation, standard error of the mean, minimum, maximum, and 95%-confidence interval for the mean were calculated. It should be mentioned here that many trials were done to increase the accuracy of the derived equation (correlation coefficient = 0.95).
However, the above empirical formula gives an error % of ±10%.
10. Comparison between Values of “ks” Obtained from Empirical Formula and Different Theoretical Methods
A comparison between the modulus of subgrade reaction ks obtained by the empirical formula and the literature data mention in Table 1 has been presented in Table 7. The values of modulus of subgrade reaction “ks” were calculated using Poisson’s ratio υ = 0.3 and the following values of Young’s modulus “Es” [kN/m2]:

From the above fair agreement has been obtained between values of ks from the empirical formula at depth of footing = 0.00 B and Biot (1937) as well as Meyerhof and Baike (1965).

Table 7. The values of “ks” for cohessionless soil [MN/m3] from the present work and the literature data.
11. Conclusions
From the present experimental study using the in-situ plate load test (P.L.T) the followings are concluded:
1) Subgrade reaction ks of cohessionless soil increases with increasing footing depth as well as footing size;
2) Subgrade reaction ks of cohessionless soil under rectangular footing is higher than that under square and that under circular one (at same equivalent area);
3) Subgrade reaction ks of cohessionless soil increases with increasing angle of internal friction;
4) The values of subgrade reaction “ks” for cohessionless soil are presented;
5) An empirical formula is presented to calculate the subgrade reaction ks of cohessionless soil for square foundation;
6) Fair agreement has been obtained between values of ks obtained from the empirical formula at depth of footing = 0.00 B and Biot (1937) as well as Meyerhof and Baike (1965).
REFERENCES
- E. Winkler, “Die Lehre von Elastizitat and Festigkeit (on Elasticity and Fixity),” Praguc, 1987, p. 182.
- B. T. Iancu and O. T. Ionut, “Numerical Analyses of Plate Loading Test Numerical Analyses of Plate Loading Test,” Buletinul Institutului Politehnic Din IASI Publicat de Universitatea Tehnică, Gheorghe Asachi,” Tomul LV (LIX), Fasc. 1, Sectia Construct II. Arhitectură (IancuBogdan Teodoru and Ionut-Ovidiu Toma), 2009, pp. 57-65.
- M. K. Elsamny, M. B. Elsedeek and W. N. Abd Elsamee, “Effect of Depth of Foundation on Modulus of Elasticity ‘Es’ for Cohessionless Soil,” Civil Engineering Researches Magazine of Al-Azhar University, Vol. 32, No. 3, 2010, p. 938.
- S. K. Dae and Y. P. Seong, “Relationship between the Subgrade Reaction Modulus and the Strain Modulus Obtained Using a Plate Loading Test,” 9th WCRR Lille World Congress, 2011.
- M. Aminaton, L. Nima, J. Masoud, Kh. Mehrdad, Kh. Mahdy, A. Payman and D. B. Ali, “Foundation Size Effect on Modulus of Subgrade Reaction on Sandy Soils,” The Electronic Journal of Geotechnical Engineering, Vol. 17, 2012, pp. 2523-2530.
- M. A. Biot, “Bending of Infinite Beams on an Elastic Foundation,” Journal of Applied Mechanics Trans. Am. Soc. Mech. Eng., Vol. 59, 1937, pp. A1-A7.
- A. B. Vesic, “Beams on Elastic Subgrade and Winkler’s Hypothesis,” Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, 1961, pp. 845-850.
- J. E. Bowles, “Foundation Analysis and Design,” 6th Edition, McGrow-Hill International Press, 1998.
- K. Terzaghi, “Evaluation of Coeffcients of Subgrade Reaction,” Géotechnique, Vol. 5, No. 4, 1955, pp. 297-326. http://dx.doi.org/10.1680/geot.1955.5.4.297
- ASTM, “Test Method for Density and Unit Weight of Soil in Place by the Rubber Balloon Method (D2167- 94),” In 1995 Annual Book of ASTM Standards, Vol. 4, No. 8, American Society for Testing and Materials, Philadelphia, 1994, pp. 167-170.
- L. S. Ping and L. W. Yang, “Subgrade Reaction and Load-Settlement Characteristics of Gravelly Cobble Deposits by Plate-Load Tests,” Canadian geotechnical Journal, Vol. 35, No. 5, 1998, pp. 801-810.
- Egyptian Code, “Soil Mechanics and Foundation,” Organization, Cairo, 2001.
- Z. M. Reza and J. Masoud, “Foundation Size Effect on Modulus of Subgrade Reaction in Clayey Soil,” The Electronic Journal of Geotechnical Engineering, Vol. 13, 2008, pp. 1-8.

