Engineering
Vol. 5 No. 9 (2013) , Article ID: 36179 , 6 pages DOI:10.4236/eng.2013.59085
Kinetics of Manganese Oxides Dissolution in Sulphuric Acid Solutions Containing Oxalic Acid
Moscow State Engineering University (MAMI), Moscow, Russia
Email: inna741@mail.ru
Copyright © 2013 I. V. Artamonova et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 27, 2013; revised March 27, 2013; accepted April 5, 2013
Keywords: Dual Electrical Layer; Acid-Base Model; The Kinetics of Manganese Oxide Dissolution; Oxalic Acid
ABSTRACT
The kinetics of the interaction of MnO2, Mn2O3, and Mn3O4, with sulphuric acid solutions and the effect of oxalic acid on this process are studied. As the sulphuric acid concentration is increased from 0.1 to 5 N, the dissolution rate of Mn2O3, Mn3O4 to MnO2 and Mn2+ ions decreases, whereas it increases with the concentration of Mn2+ ions. Upon the addition of H2Ox, the complete dissolution of Mn3O4 occurs more quickly. The reaction order with respect to the H+ and 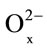 ions is +0.5 ± 0.1. A mechanism of MnO2 dissolution promotion by
ions is +0.5 ± 0.1. A mechanism of MnO2 dissolution promotion by  is proposed. The dissolution rate was found to depend on the concentrations of
is proposed. The dissolution rate was found to depend on the concentrations of 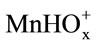 and
and  ions and was highest at pH 1.6 ± 0.2. A rate law and mechanism are suggested for manganese oxides dissolution.
ions and was highest at pH 1.6 ± 0.2. A rate law and mechanism are suggested for manganese oxides dissolution.
1. Introduction
To accelerate the etching of manganese alloys and optimise the dressing and leaching of manganese oxide ores, it is necessary to understand the mechanisms of these processes [1-12]. The most promising method of improving the effectiveness of the etching of manganese oxides is reductive dissolution by various complexing agents [5-10]. However, the rate-limiting step has not been identified in most works on the reductive dissolution of oxides.
2. Material and Method
In the study of dissolution kinetics, we used extra-pure γ-MnO2, Mn2O3 and Mn3O4 powder with a particle size of 60 - 80 μm. A sample of oxide weighing 0.362 ± 0.005 g was placed in a temperature-controlled reaction vessel containing 0.750 ± 0.005 l of an aqueous solution of sulphuric and oxalic acids. During dissolution, the mixture was stirred magnetically at ν = 600 - 700 rpm. In preliminary runs, the dissolution rate was almost independent of ν for ν > 500 rpm. The pH of the solution was adjusted by adding sulphuric acid. The concentration of sulphuric acid was varied between 0.005 and 2.5 mol/l. Most measurements were carried out at 353 K. The solution was sampled at regular intervals using an N16 Schott filter. The manganese in solution was determined photocolourimetrically as the complex with formaldoxime [13]. The non-stoichiometric composition change during the dissolution of oxides phases in sulphuric acid was measured by a technique described in a previous study [14].
3. Results and Discussion
3.1. Analysis of the Kinetic Data of Manganese Oxide Dissolution (Mn2O3, Mn3O4 and MnO2) in Sulphuric Acid
As seen in Figures 1-3, a remarkable feature of the interaction of manganese oxide with sulphuric acid is that the oxide is dissolved incompletely. The process is terminated at α = 0.66 (α is the ratio of the concentration of Mn2+ ions in the solution to the total manganese in the oxide sample).
Based on the data shown in Figures 1 and 2, the dissolution rates of Mn2O3 and Mn3O4 decrease with increasing sulphuric acid concentration.
3.2. Calculation of the Specific Rate of Dissolution
Using these curves (Figures 1-3), we derived the specific dissolution rate W, the apparent orders of reaction with respect to hydrogen ions and manganese (II) ions, and

Figure 1. Dependence of the extent of dissolution of Mn3O4 (α) on the time t at 353 K for various sulphuric acid concentrations: (1) 2.5, (2) 1.5, (3) 1.0, (4) 0.75, (5) 0.5, (6) 0.25 and (7) 0.05 mol/l. Points—experimental data, lines—calculation of the chain mechanism equation.
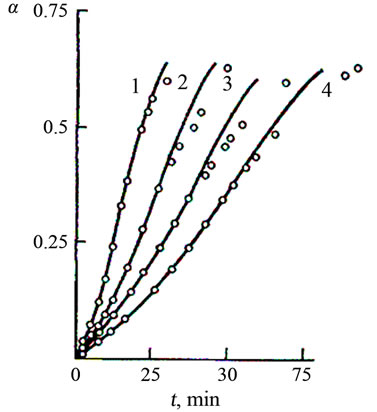
Figure 2. Dependence of the extent of dissolution of Mn2O3 (α) on the time t at 353 K for various sulphuric acid concentrations: (1) 0.1, (2) 0.51, (3) 0.91 (4) 2.71 mol/l. Points— experimental data, lines—calculation of the chain mechanism equation.
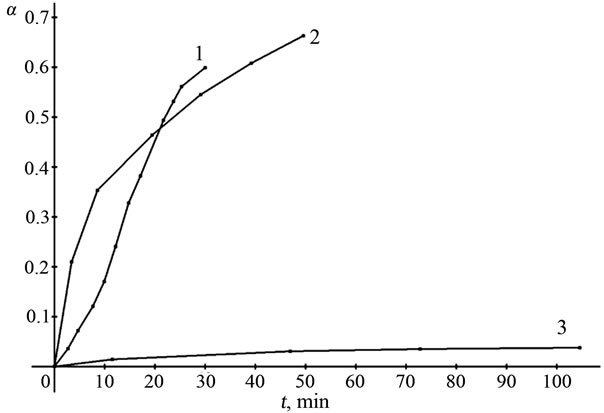
Figure 3. Dependence of the extent of dissolution of manganese oxides (α) on the time t at 353 K, 0.05 mol/l sulphuric acid: (1) Mn2O3, (2) Mn3O4, (3) MnO2.
the activation energy of dissolution by testing various heterogeneous kinetic models (Table 1) using affine transformations. First, we plotted α against t/t0.5, where t0.5 is the time required for 50% of the sample to dissolve.

Table 1. Heterogeneous kinetic models and their equations.
To select the heterogeneous kinetics equations that best fit the experimental curves, the obtained α versus t/t0.5 dependences were described by various theoretical dependences.
The choice of the equation routinely began with the most simple equation, (e). The compressed sphere equation is not applicable because the curves are s-shaped and correspond to the Fisher criterion.
The best results were obtained with the Hill function (1), which corresponds to the formation of active sites at the dislocations and grain boundaries of the oxide phase [15].
The theoretical lines well describe the experimental points (Figures 1 and 2), proving the applicability of the chosen Equation (1).
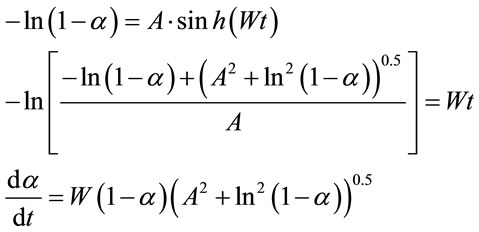 (1)
(1)
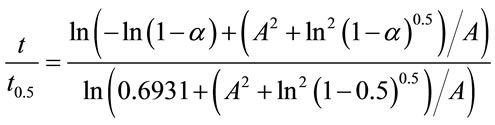 (2)
(2)
The obtained A values (A = 0.2) were used to calculate the specific rate of dissolution (disproportionation).
 (3)
(3)
where τ0.5 = Wt0.5(τ0.5 = 0.65).
Using Equation (1) it is possible to calculate the specific rate of dissolution for the given concentration (Tables 2 and 3).
The activation energy of the process calculated from the log W versus 1/T dependence gives Ea = 80 ± 0.5 kJ/mol.
We found that the dissolution rates of Mn2O3 and Mn3O4 decrease as [H+] is increased, which is attributed to the disproportionation reactions, resulting in incomeplete dissolution.
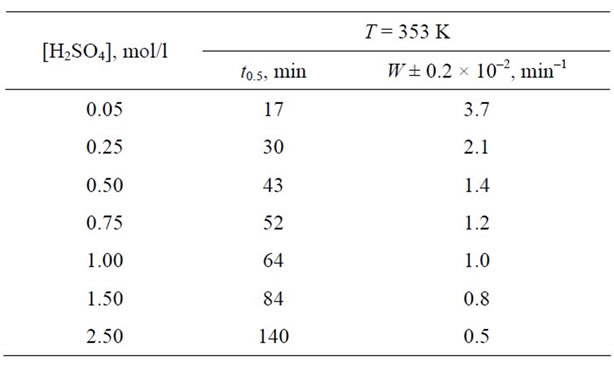
Table 2. Kinetic constants for the dissolution of Mn3O4 in sulphuric acid solutions as a function of H2SO4 concentration.
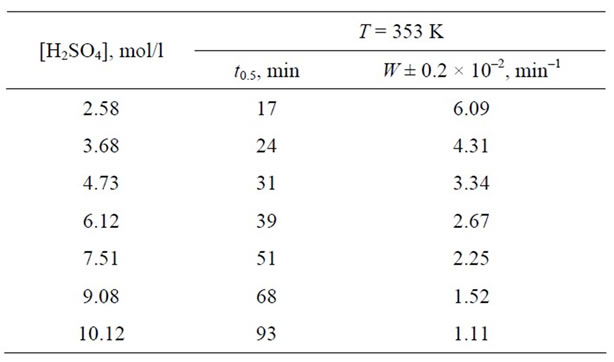
Table 3. Kinetic constants for the dissolution of Mn2O3 in sulphuric acid solutions as a function of H2SO4 concentration.
The process can be represented as disproportionate according to the following scheme:
 (4)
(4)
where x1 and x are the initial and final x = [O]/[Mn] ratios for the oxide phase.
Equation (4), Figure 4, and Table 4 both indicate a dependence between the extent of dissolution (α) and non-stoichiometric composition (х) with time, which can be expressed using the following equation [14]:
 (5)
(5)
The orders of the disproportionation reaction determined from logW versus pH and logw versus log[Mn2+] are as follows:
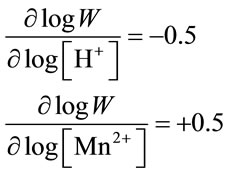 (6)
(6)
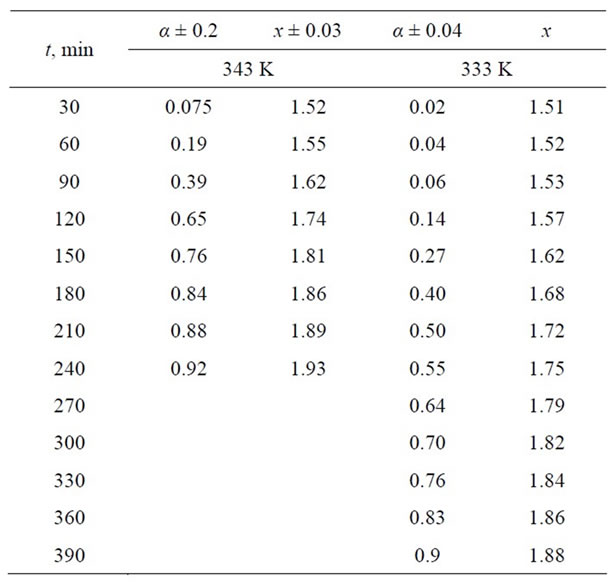
Table 4. Dependence of the extent of dissolution Mn2O3 and non-stoichiometric index (х) of oxygen in MnOx for time (t) in sulphuric acid at various temperatures.
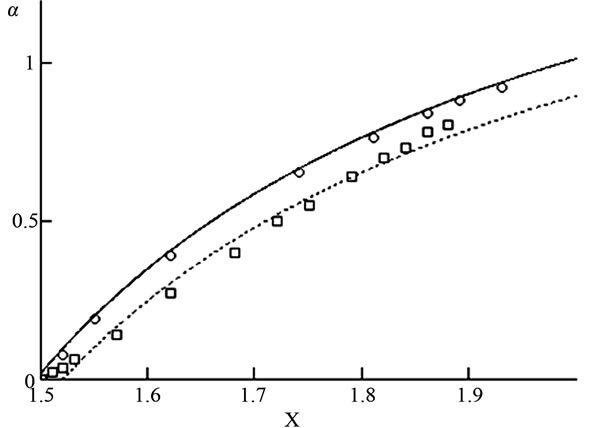
Figure 4. Dependence of the extent of dissolution (α) of Mn2O3 on the stoichiometric composition of manganese oxides (x = [O]/[Mn]). Lines—calculations from Equation (2), points—experimental data.
A preliminary consideration of the effect of different factors on the kinetics of the process shows that the obtained curves are rectified in the 1/W versus [H+] and 1/W versus [Mn2+] coordinates. This observation allows us to describe the interaction rate of manganese oxides with H2SO4 by the equation:
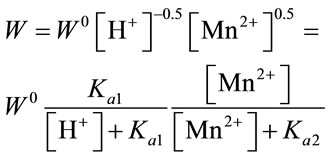 (7)
(7)
where Kal, Ka2 and W0 are kinetic constants.
We propose a Mn2O3 dissolution mechanism that explains the negative orders for protons and positive orders for manganese ions [6]:
1) Hydration of an oxide surface:
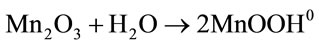 (8)
(8)
2) Adsorption of protons:
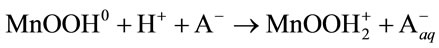 (9)
(9)
3) Dissolution from active sites:
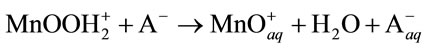 (10)
(10)
4) Volumetric reaction:
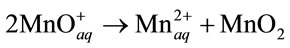 (11)
(11)
Integrally:
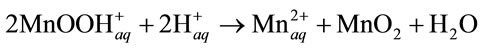 (12)
(12)
The disproportionation of Mn3O4 characterised by two-stage kinetics (Figure 1) can be represented by two overall reactions:
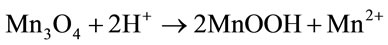 , (13)
, (13)
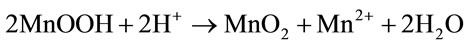 (14)
(14)
In both cases, low-solubility MnO2 is formed on the oxide surfaces.
Therefore, it is important to determine the conditions that promote the efficient dissolution MnO2.
The kinetics of manganese dioxide dissolution were then studied in sulphuric acid solutions containing oxalic acid.
3.3. Kinetics Analysis of the Effect of Oxalic Acid on the Rate of the Interaction and Dissolution of MnO2 in Sulphuric Acid Solutions
Influence of concentration of oxalic acid. The results of the dissolution of manganese dioxide in various concentrations of oxalic acid are shown in Figure 5. Based on Figure 4, increasing the oxalate ion concentration increases the extent of dissolution (α). Thus, full dissolution is observed.
The specific dissolution rate increases with oxalic acid concentration at a constant sulphuric acid concentration. The plot of this dependence (Figure 5) resembles that of an adsorption isotherm. The dissolution rate follows the empirical equation:
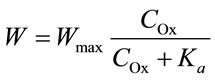 (15)
(15)
The Langmuir and Freundlich isotherms describe the experimental data with identical accuracies; therefore, the following is used as a first approximation:
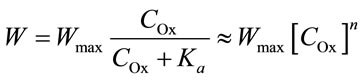 (16)
(16)

Figure 5. Dependence of the extent of MnO2 dissolution (α) on the time (t) at [H2SO4] = 0.05 mol/l and various oxalic acid concentrations: (1) 0.050, (2) 0.075, (3) 0.010, (4) 0.020, (5) 0.030, and (6) 0.04 mol/l (T = 353 K, pH = 1.5, V = 750 ml).
where n is the reaction order with respect to oxalic acidand 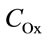 is the total concentration of all forms of oxalic acid (n = 0.66, Ka = 0.026 mol/l, Wmax = 0.66 min–1).
is the total concentration of all forms of oxalic acid (n = 0.66, Ka = 0.026 mol/l, Wmax = 0.66 min–1).
When 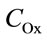 tends to infinity, the process rate reaches its maximum, Wmax.
tends to infinity, the process rate reaches its maximum, Wmax.
Influence of рН at constant oxalic acid concentration. The dissolution rate of manganese (IV), (III) oxides was studied as a function of pH in solutions containing 0.005 M oxalic acid. We found that W is highest at pH 1.6 ± 0.2 (Figure 6).
From the kinetic data obtained, the following relation was derived for the dissolution of MnO2 in oxalic acid [16-19]:
 , (17)
, (17)
where θi is the coverage of the MnO2 surface by species i.
3.4. Modelling the Manganese (IV) Oxide Dissolution Mechanism
According to the site-binding model [16-19], dissolution proceeds via the formation of intermediates when the surface is positively charged.
Scheme 1:

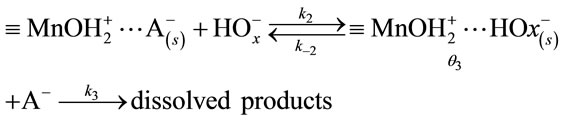
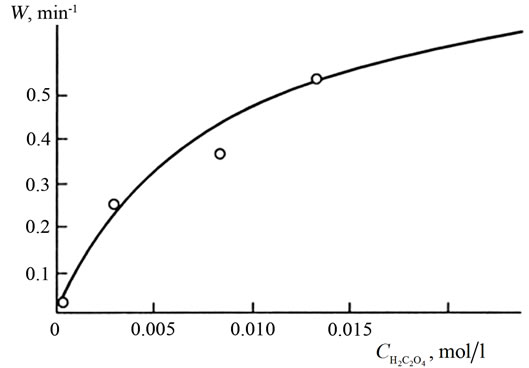
Figure 6. Specific rate of MnO2 dissolution as a function of oxalic acid concentration at T = 353 K and pH 1.5. Lines— calculatio using Equations (13) and (16) or (20), points— experimental data.
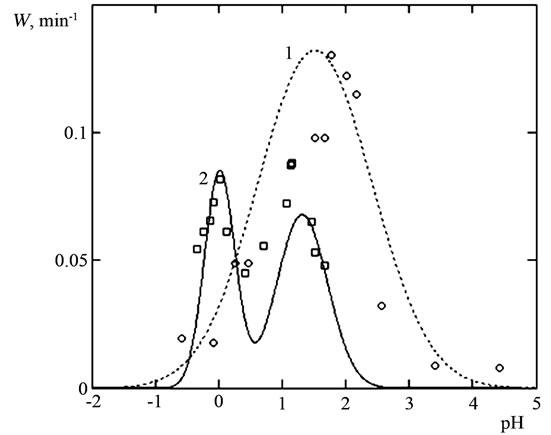
Figure 7. Specific rate of MnO2 (1) and Mn2O3 (2) dissolution as function of pH at COx =0.005 mol/l and T = 353 K. Lines—calculatio using Equation (17), points—experimental data.
here, θ1 is the fraction of the unbound oxide surface and θ2 and θ3 are the coverages of the surface by 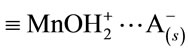 and
and 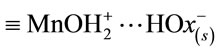 complexes, respectively. In this case, the dissolution rate may be limited by the passage of the intermediate complex into solution, which occurs at a rate proportional to θ3. W and θ3 can be determined as functions of various parameters by applying the method based on a steady-state approximation and the principle of detailed balancing [16-19] to the steps preceding the rate-limiting step.
complexes, respectively. In this case, the dissolution rate may be limited by the passage of the intermediate complex into solution, which occurs at a rate proportional to θ3. W and θ3 can be determined as functions of various parameters by applying the method based on a steady-state approximation and the principle of detailed balancing [16-19] to the steps preceding the rate-limiting step.
The dissolution rate at constant pH is given by:
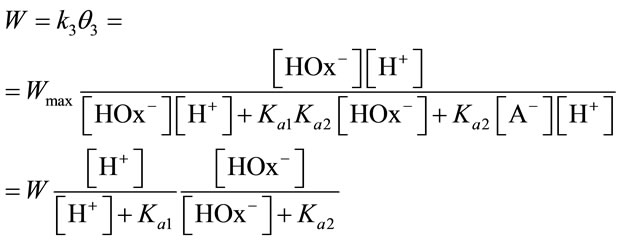 (14)
(14)
with Wmax = 0.37 ± 0.05 min–1, Kal = {k–1k–2 + k3(k–1 + k2)}/(k1k2) = 2 × 10–3 mol/l and Ka2 = (k–2 + k3)/k2 = 4 × 10–3 mol/l. Here, Ka1 and Ka2 are the equilibrium constants of adsorption at the dioxideelectrolyte interface.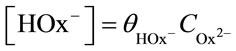 , where
, where 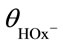 is the fraction of
is the fraction of 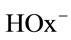 ions in solution:
ions in solution:
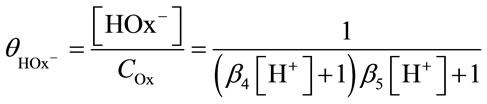 (20)
(20)
where β4 and β5 are the dissociation constants of oxalic acid: log β4 = 1.271, log β5 = 4.266 [12-16].
4. Conclusions
The dissolution of manganese oxides in sulphuric acid proceeds to partial completion, whereas the addition of oxalic acid allows it to proceed to completion.
Thus, the performed experimental and theoretical investigation of the dissolution and disproportionation processes of manganese oxides in H2SO4 solutions in the presence of H2Ox indicated that the dissolution mechanism involves the adsorption of H2Ox followed by the reduction of the surface layers of the oxide.
The dissolution of manganese dioxide in sulphuric acid solutions containing oxalic acid can be accelerated considerably. The dissolution rate is affected by the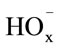 ,
, 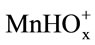 , and H+ ions. The maximum dissolution rate is observed at pH 1.6 and a 1:5 concentration ratio for the manganese ions and oxalic ions.
, and H+ ions. The maximum dissolution rate is observed at pH 1.6 and a 1:5 concentration ratio for the manganese ions and oxalic ions.
The first step in manganese dioxide dissolution is the coadsorption of 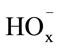 and
and 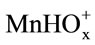 ions, followed by charge transfer. The resulting
ions, followed by charge transfer. The resulting  ions pass into solution. The rate-limiting step is three-dimensional nucleation on the MnO2 surface.
ions pass into solution. The rate-limiting step is three-dimensional nucleation on the MnO2 surface.
5. Acknowledgements
This work was supported by the Ministry of Education of the Russian Federation (state contracts № 14.740.11. 1095, № 3.5258.2011).
REFERENCES
- M. A. Blesa, I. M. Perdo and A. E. Regazzoni, “Chemical Dissolution of Metal Oxides,” CRC Press, Boca Ration, 1994.
- S. O. Lee, T. Tran, Y. Y. Park, S. J. Kim and M. J. Kim, “Study on the Kinetics of Iron Leaching by Oxalic Acid,” International Journal of Mineral Processing, Vol. 80, No. 2-4, 2006, pp. 144-152.
- S. K. Mindal and P. C. Banerjee, “Iron Leaching with Oxalic Acid: Effects of Different Physico-Chemical Parameters,” International Journal of Mineral Processing, Vol. 74, No. 1-4, 2004, pp. 263-270.
- С. I. Nwoye, “Model for Computational Analysis of Dissolved Haematite and Heat Absorbed by Oxalic Acid Solution during Leaching of Iron Oxide Ore,” Journal of Engineering and Applied Science, Vol. 4, 2008, pp. 22- 25.
- D. Panias, M. Taxiarchou, I. Paspaliaris and A. Kontopoulos, “Mechanisms of Dissolution of Iron Oxides in Aqueous Oxalic Acid Solutions,” Hydrometallurgy, Vol. 42, No. 2, 1996, pp. 257-265. doi:10.1016/0304-386X(95)00104-O
- D. Panias, M. Taxiarchou, I. Paspaliaris and A. Kontopoulos, “Termodynamic Analysis of the Reactions of Iron Oxides: Dissolution in Oxalic Acid,” Canadian Metallurgical Quarterly, Vol. 35, No. 4, 1996, pp. 363-373. doi:10.1016/S0008-4433(96)00018-3
- Y. Wang and A. T. Stone, “Reaction of Mn(III,IV)(hydr) Oxades with Oxalic Acid, Glioxylic Acid, Phosphonoformic Acid, Compounds,” Geochimica et Cosmochimica Acta, Vol. 70, 2006, pp. 4477-4490. doi:10.1016/j.gca.2006.06.1548
- Y. Wang Y. and A. T. Stone, “The Citric Acid-Mn(III,IV) O2(s,birnessite) Reaction. Electron Transfer, Complex Formation,” Geochimica et Cosmochimica Acta, Vol. 70, 2006, pp. 4463-4476. doi:10.1016/j.gca.2006.06.1551
- A. T. Stone, “Reductive Dissolution of Manganese(III)/ (IV) Oxide by Subsituted Phenols,” Environmental Science & Technology, Vol. 21, No. 4, 1987, pp. 979-988. doi:10.1021/es50001a011
- A. T. Stone, “Reduction and Dissolution of Manganese (III) and Manganese(IV) Oxides by Organics,” Environmental Science & Technology, Vol. 18, No. 2, 1984, pp. 450-456. doi:10.1021/es00124a011
- A. T. Stone and I. I. Morgan, “Reductive Dissolution of Metal Oxides, in Aquatic Surface Chemistry,” Wiley, New York, 1987.
- A. T. Stone and H. J. Urion, “Kinetics and Reaction Stoichiometry in the Reductive Dissolution of Manganese(IV) Dioxide and Co(III) Oxide by Hydrocarbons,” Journal of Colloid and Interface Science, Vol. 132, No. 2, 1989, pp. 509-522. doi:10.1016/0021-9797(89)90265-8
- A. K. Lavrukhina and L. V. Yutkina, “Analiticheskaya Khimiya Margantsa (Analytical Chemistry of Manganese),” Nauka, Moscow, 1974.
- K. Vetter and N. Jaeger, “The Mechanism of Occurrence of Potential of an Electrode from Manganese Dioxide,” In: A. I. Frumkin, Ed., The Basic Questions of Modern Theoretical Electrochemistry, Mir, Moscow, 1965, pp. 253- 262.
- B. Delmon, “Introduction a la Cinetique Heterogene, Paris: Technip,” Mir, Moscow, 1972.
- W. F. Tan, S. J. Lu, F. Liu, X. H. Feng, J. Z. He and L. K. Koopal, “Determination of the Point-Of-Zero Charge of Manganese Oxides with Different Methods Including an Improved Salt Titration Method,” Soil Science, Vol. 173, No. 4, 2008, pp. 277-286. doi:10.1097/SS.0b013e31816d1f12
- V. V. Batrakov, I. G. Gorichev and N. A. Kipriyanov, “Influence of a Double Electric Layer on the Kinetics Dissolution Oxides Metals,” Elektrokhim, Vol. 30, No. 4, 1994, pp. 444-458.
- R. Schmidt and V. N. Sapunov, “Neformalnaya kinetika,” Mir, Moscow, 1985.
- A. A. Bezdenezhnykh, “Inzhenernye Metody Sostavleniya Uravnenii Skorostei Reaktsii i Rascheta Kineticheskikh Konstant (Engeneering Techniques of Formulation of Equations for Reaction Rates and Calculation of Kinetic Constants),” Khimiya, Leningrad, 1974.

