Engineering
Vol. 3 No. 1 (2011) , Article ID: 3720 , 4 pages DOI:10.4236/eng.2011.31004
Fractional Order Generalized Thermoelastic Infinite Medium with Cylindrical Cavity Subjected to Harmonically Varying Heat
Faculty of Engineering-Umm Al-Qura University, Makkah, Saudi Arabia
E-mail: yousefanne@yahoo.com
Received October 23, 2010; revised November 26, 2010; accepted December 16, 2010
Keywords: Thermoelasticity, Generalized Thermoelasticity, Fractional Order, Cylindrical Cavity, Harmonically Heat
ABSTRACT
In this work, a mathematical model of an elastic material with cylindrical cavity will be constructed. The governing equations will be taken into the context of the fractional order generalized thermoelasticity theory (Youssef 2010). Laplace transform and direct approach will be used to obtain the solution when the boundary of the cavity is exposed to harmonically heat with constant angular frequency of thermal vibration. The inverse of Laplace transforms will be computed numerically using a method based on Fourier expansion techniques. Some comparisons have been shown in figures to present the effect of the fractional order parameter and the angular frequency of thermal vibration on all the studied felids.
1. Introduction
Recently, a considerable research effort has been expended to study anomalous diffusion, which is characterized by the time-fractional diffusion-wave equation by Kimmich [1]:
 , (1)
, (1)
where 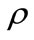 is the mass density, c is the concentration,
is the mass density, c is the concentration, 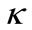 is the diffusion conductivity,
is the diffusion conductivity, 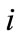 is the coordinate symbol which takes the values 1, 2 and 3, the subscript “,” means the derivative with respect to xi and notion
is the coordinate symbol which takes the values 1, 2 and 3, the subscript “,” means the derivative with respect to xi and notion  is the Riemann-Liouville fractional integral is introduced as a natural generalization of the well-known n-fold repeated integral
is the Riemann-Liouville fractional integral is introduced as a natural generalization of the well-known n-fold repeated integral 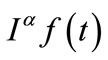 written in a convolution-type form as in [2,3]:
written in a convolution-type form as in [2,3]:
 (2)
(2)
where  is the gamma function.
is the gamma function.
According to Kimmich [1] Equation (1) describes different cases of diffusion where  correspond to weak diffusion (sub diffusion),
correspond to weak diffusion (sub diffusion),  correspond to normal diffusion,
correspond to normal diffusion, 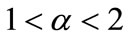 correspond to strong diffusion (super diffusion) and
correspond to strong diffusion (super diffusion) and  correspond to ballistic diffusion.
correspond to ballistic diffusion.
It should be noted that the term diffusion is often used in a more generalized sense including various transport phenomena. Equation (1) is a mathematical model of a wide range of important physical phenomena, for example, the sub-diffusive transport occur in widely different systems ranging from dielectrics and semiconductors through polymers to fractals, glasses, porous, and random media. Super diffusion is comparatively rare and has been observed in porous glasses, polymer chain, biological systems, transport of organic molecules and atomic clusters on surface [4]. One might expect the anomalous heat conduction in media where the anomalous diffusion is observed.
Fujita [5,6] considered the heat wave equation for the case of :
:
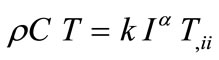 , (3)
, (3)
where C is the specific heat, k is the thermal conductivity and the subscript “,” means the derivative with respect to the coordinates .
.
Equation (3) can be obtained as a consequence of the non local constitutive equation for the heat flux components  is in the form
is in the form
 . (4)
. (4)
Povstenko [4] used the Caputo heat wave equation defines in the form:
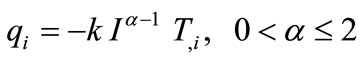 , (5)
, (5)
to get the stresses corresponding to the fundamental solution of a Cauchy problem for the fractional heat conduction equation in one-dimensional and two-dimensional cases.
Some applications of fractional calculus to various problems of mechanics of solids are reviewed in the literature [7,8].
2. Theory of Fractional Order Generalized Thermoelasticity
The classical thermoelasticity is based on the principles of the theory of heat conduction which is called Fourier law, which relates the heat flux components  to the temperature gradient as follows:
to the temperature gradient as follows:
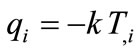 . (6)
. (6)
In combination with the energy conservative law, this leads to the parabolic heat conduction equation which is considered by Povstenko [4]:
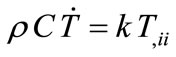 , (7)
, (7)
where dotted above T means the derivative with respect to the time t.
Recently, in the non classical thermoelasticity theories, Fourier law (6) and heat conduction (7) are replaced by more general equations, have been formulated. The first well-known generalized of such a type of Lord and Shulman [9] and it takes the form:
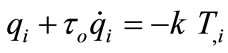 , (8)
, (8)
which leads to the hyperbolic differential equation of heat conduction of Lord and Shulman [9]:
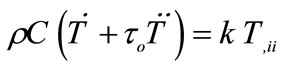 , (9)
, (9)
where 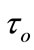 is non-negative constant and is called relaxation time.
is non-negative constant and is called relaxation time.
According to equation (9), Kaliski [10] and Lord and Shulman [9] constructed the theory of generalized thermoelasticity.
In the context of the generalized thermoelasticity, the governing equations for isotropic medium are defined as follows:
The equation of motion
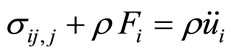 . (10)
. (10)
The constitution relation
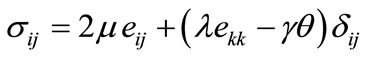 , (11)
, (11)
where  are Lamé's constant,
are Lamé's constant,  is the displacement component,
is the displacement component, 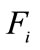 the body force component,
the body force component, 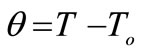 is the increment of the dynamical temperature where
is the increment of the dynamical temperature where 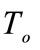 is the reference temperature,
is the reference temperature,  where
where  is called the thermal expansion coefficient, where δij is the Kronecker delta symbol,
is called the thermal expansion coefficient, where δij is the Kronecker delta symbol,  is the stress tensor such that
is the stress tensor such that  and
and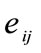 is the strain tensor satisfy the relations
is the strain tensor satisfy the relations
 . (12)
. (12)
The heat flux equation
 . (13)
. (13)
The entropy increment equation per unit volume takes the form
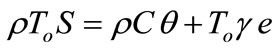 , (14)
, (14)
where  is the entropy increment of the material.
is the entropy increment of the material.
The heat flux-entropy equation
 . (15)
. (15)
The heat equation without any heat sources
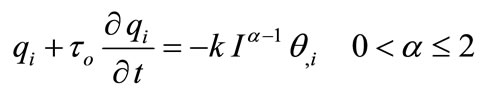 . (16)
. (16)
By using Equations (14,15,16), we have the heat equation in the form [11]:
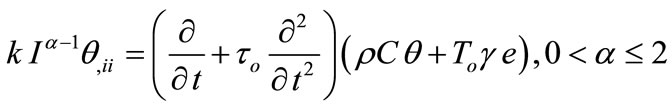 (17)
(17)
where 
3. The Problem Formulation
Let us consider a perfectly conducting elastic infinite body with cylindrical cavity occupies the region 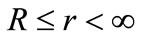 of an isotropic homogeneous medium whose state can be expressed in terms of the space variable r and the time variable t such that all of the state functions vanish at infinity. We will use the cylindrical system of coordinates (r,y,z) with the z-axis lying along the axis of the cylinder. Due to symmetry, the problem is one-dimensional with all the functions considered depending on the radial distance r and the time t.
of an isotropic homogeneous medium whose state can be expressed in terms of the space variable r and the time variable t such that all of the state functions vanish at infinity. We will use the cylindrical system of coordinates (r,y,z) with the z-axis lying along the axis of the cylinder. Due to symmetry, the problem is one-dimensional with all the functions considered depending on the radial distance r and the time t.
The medium described above is considered to be quiescent and the surface of the cavity is subjected to harmonically varying heat and traction free described mathematically as follow:
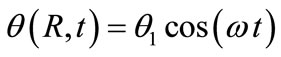 , (18)
, (18)
and
 , (19)
, (19)
where  is constant and
is constant and 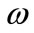 is the angular frequency of thermal vibration (
is the angular frequency of thermal vibration ( for a thermal shock).
for a thermal shock).
It is assumed that there are no body forces and no heat sources in the medium. Thus, the field equations (10), (11), (12) and (17) in cylindrical case can be set as [12]:
 , (20)
, (20)
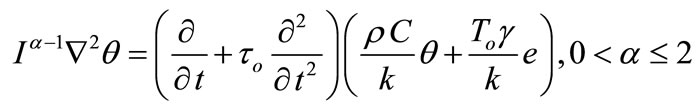 (21)
(21)
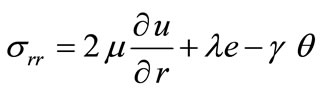 , (22)
, (22)
 (23)
(23)
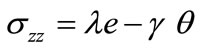 , (24)
, (24)
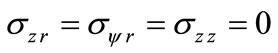 , (25)
, (25)
 , (26)
, (26)
where 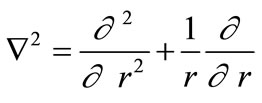
For convenience, we shall use the following non-dimensional variables [12]:
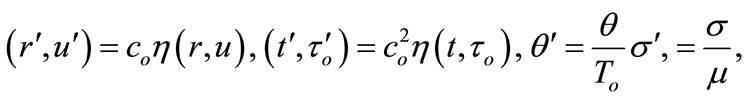
where  and
and .
.
Equations (20-26) assume the form (where the primes are suppressed for simplicity)
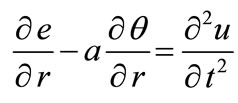 , (27)
, (27)
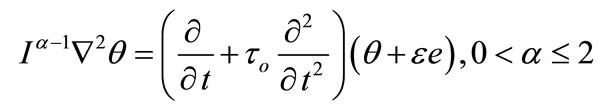 , (28)
, (28)
 , (29)
, (29)
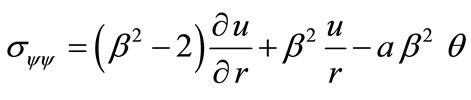 , (30)
, (30)
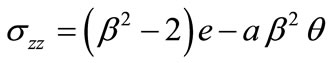 , (31)
, (31)
where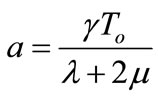 ,
,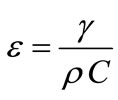 ,
,  and
and 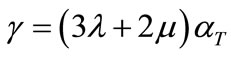 .
.
4. Formulation in the Laplace Transform Domain
Taking the Laplace transform for the both sides of the Equations (27-31), this is defined as follows:
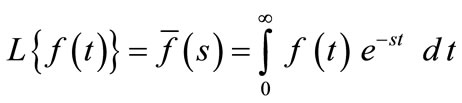 , (32)
, (32)
where the rule for the Laplace transform of the Riemann-Liouville fractional integral for zero initial function reads from Povstenko [4]:
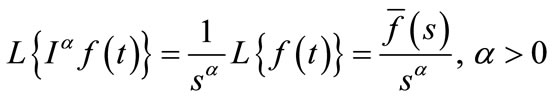 . (33)
. (33)
Then, we have
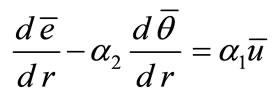 , (34)
, (34)
 , (35)
, (35)
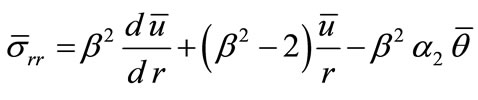 (36)
(36)
 , (37)
, (37)
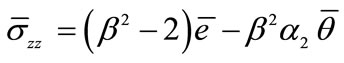 , (38)
, (38)
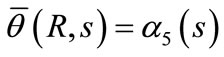 , (39)
, (39)
 , (40)
, (40)
where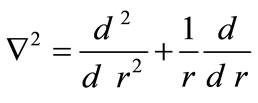 ,
, ,
, ,
, 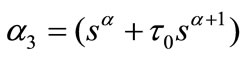 ,
, 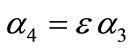 ,
, 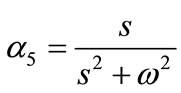 and an over bar symbol denotes its Laplace transform and s denotes the Laplace transform parameter.
and an over bar symbol denotes its Laplace transform and s denotes the Laplace transform parameter.
Eliminating u from the Equations (26,34,35), we get
 , (41)
, (41)
 . (42)
. (42)
Eliminating  from Equations (41,42), we obtain
from Equations (41,42), we obtain
 . (43)
. (43)
In a similar manner, we can show that  satisfies the equation
satisfies the equation
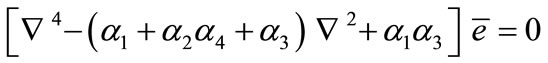 . (44)
. (44)
The bounded solutions of Equations (41,42) at infinity can be written in the form
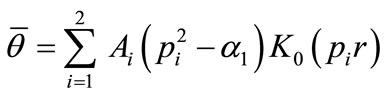 , (45)
, (45)
 , (46)
, (46)
where Ko(.) is the modified Bessel function of the second kind of order zero. A1, A2, B1 and B2 are all parameters depending on the parameter s of the Laplace transform,  and
and 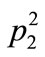 are the roots of the characteristic equation
are the roots of the characteristic equation
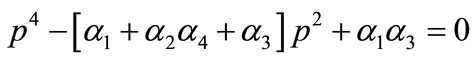 , (47)
, (47)
and satisfy the relations
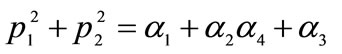 ,
,
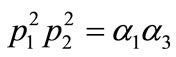 .
.
Using Equation (41), we obtain
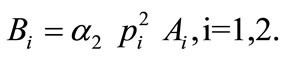 (48)
(48)
Thus, we have
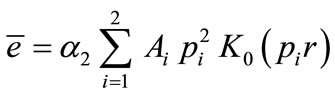 . (49)
. (49)
Substituting from Equation (49) into the Laplace transform of Equation (26), we obtain
 , (50)
, (50)
where K1(.) is the modified Bessel function of the second kind of order one.
In deriving Equation (50), we have used the following well-known relation of the Bessel function:
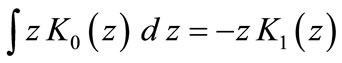 Finally, substituting from Equations (45,49,50) into Equations (36-38), we obtain the stress components in the form:
Finally, substituting from Equations (45,49,50) into Equations (36-38), we obtain the stress components in the form:
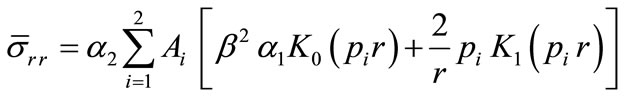 , (51)
, (51)
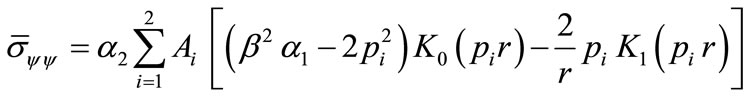 (52)
(52)
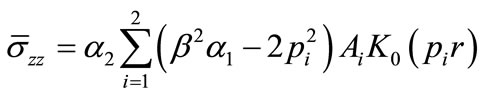 . (53)
. (53)
Using the boundary conditions (39,40), we get
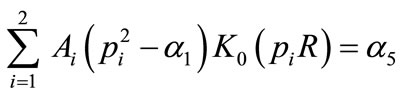 , (54)
, (54)
 . (55)
. (55)
Then, we have
 , (56)
, (56)
where
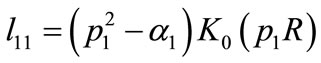 ,
,  ,
,
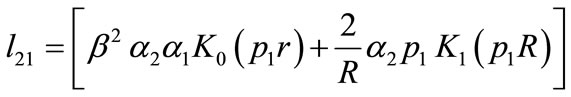 ,
,
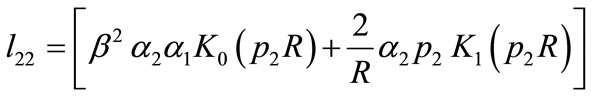 .
.
Then, we have
 and
and
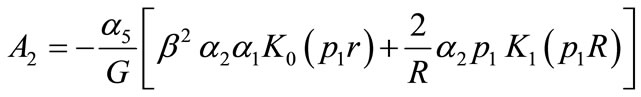 where
where

Those complete the solution in the Laplace transform space.
5. Numerical Inversion of the Laplace Transform
In order to invert the Laplace transform, we adopt a numerical inversion method based on a Fourier series expansion [13].
By this method the inverse 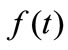 of the Laplace transform
of the Laplace transform 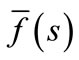 is approximated by
is approximated by
 (57)
(57)
where N is a sufficiently large integer representing the number of terms in the truncated Fourier series, chosen such that
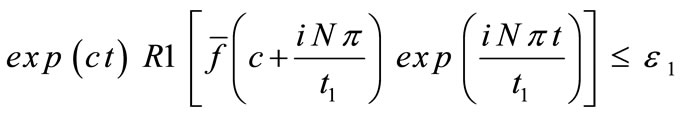 (58)
(58)
where e1 is a prescribed small positive number that corresponds to the degree of accuracy required. The parameter c is a positive free parameter that must be greater than the real part of all the singularities of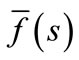 . The optimal choice of c was obtained according to the criteria described in [13].
. The optimal choice of c was obtained according to the criteria described in [13].
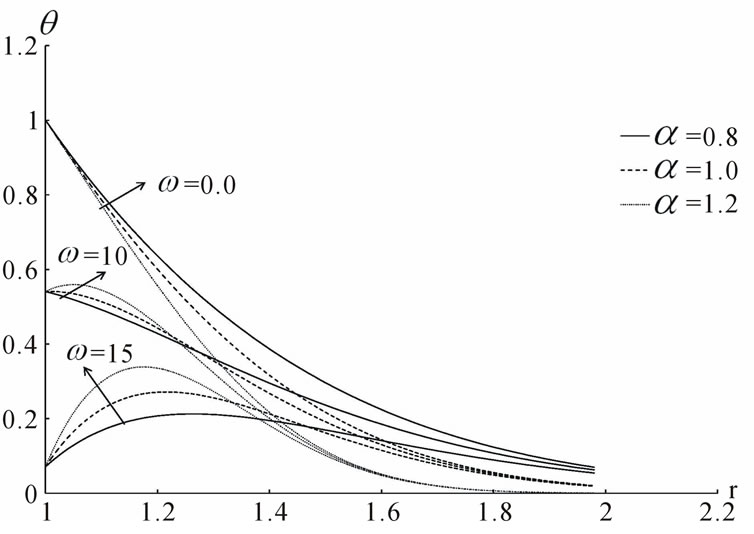
Figure 1. The temperature distribution.
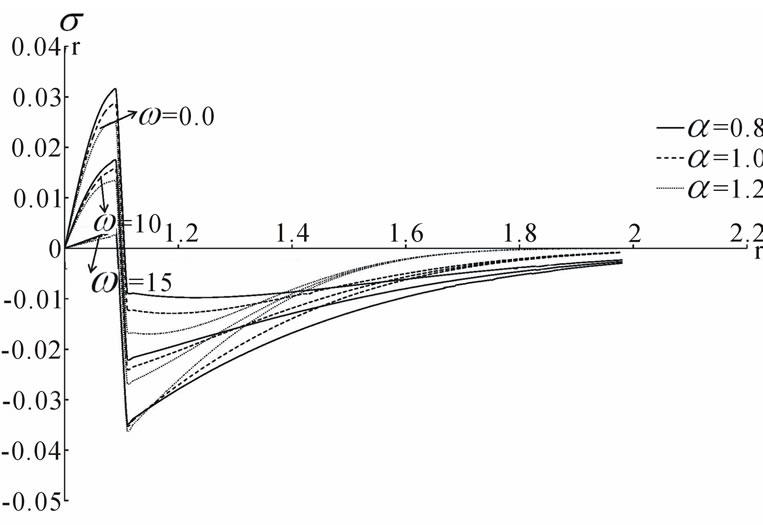
Figure 2. The radial stress distribution.

Figure 3. The stress 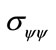 distribution.
distribution.

Figure 4. The displacement distribution.

Figure 5. The strain distribution.
6. Numerical Results and Discussion
With a view to illustrating the analytical procedure presented earlier, we now consider a numerical example for which computational results are given. The results depict the variation of temperature, stress, displacement and strain fields in the context of Youssef model [11].
For this purpose, copper is taken as the thermoelastic material for which we take the following values of the different physical constants [12]:
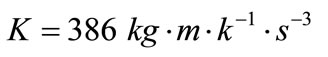 ,
,  ,
,
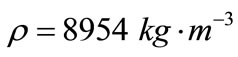 ,
, 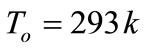 ,
, 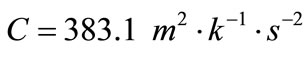 ,
,
 ,
,
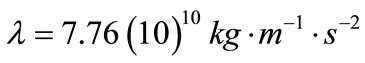 .
.
From the above values we get the nondimensional values for our problem as:
 .
.
The results of the temperature, the stresses, the displacement and the strain are shown in Figures 1-5 respectively with wide range of non dimensional distance r from r = R = 1.0 up to r = 2.0, non dimensional time t = 0.08 and non dimensional relaxation time 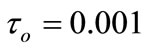 with different values of the parameter
with different values of the parameter 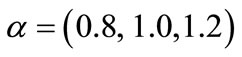 which describe the three types of conductivity (weak conductivity, normal conductivity, strong conductivity), respectively and with different values of the parameter
which describe the three types of conductivity (weak conductivity, normal conductivity, strong conductivity), respectively and with different values of the parameter . We can see the significant effect of the parameter
. We can see the significant effect of the parameter 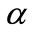 and the angular frequency of thermal vibration
and the angular frequency of thermal vibration 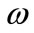 on all the studied fields.
on all the studied fields.
7. Conclusion
We considered a perfectly conducting elastic isotropic homogeneous infinite body with cylindrical cavity in the context of the fractional order generalized thermoelasticity theory (Youssef model). The effect of the fractional parameter and the angular frequency of thermal vibration on all the studied fields are very significant. New classification of the materials must be constructed according to the fractional parameter which describes the ability of the material to conduct the heat.
8. REFERENCES
- R. Kimmich, “Strange Kinetics, Porous Media, and NMR,” Chemical Physics, Vol. 284, 2002, pp. 243-285. doi:10.1016/S0301-0104(02)00552-9
- I. Podlubny, “Fractional Differential Equations,” Academic Press, New York, 1999.
- F. Mainardi and R. Gorenflo, “On Mittag-Lettler-Type Function in Fractional Evolution Processes,” Journal of Computational and Applied Mathematics, Vol. 118, No. 1-2, 2000, pp. 283-299. doi:10.1016/S0377-0427(00)002 94-6
- Y. Z. Povstenko, “Fractional Heat Conductive and Associated Thermal Stress,” Journal of Thermal Stress, Vol. 28, 2005, pp. 83-102. doi:10.1080/014957390523741
- Y. Fujita, “Integrodifferential Equation Which Interpolates the Heat Equation and Wave Equation (I),” Osaka Journal of Mathematics, Vol. 27, 1990, pp. 309-321.
- Y. Fujita, “Integrodifferential Equation Which Interpolates the Heat Equation and Wave Equation (II),” Osaka Journal of Mathematics, Vol. 27, 1990, pp. 797-804.
- Y. N. Rabotnov, “Creep of Structure Elements,” Naka, Moscow, 1966.
- Y. A. Rossikhin and M. V. Shitikova, “Applications of Fractional Calculus to Dynamic Problems of Linear and Non Linear Hereditary Mechanics of Solids,” Applied Mechanics Reviews, Vol. 50, No.1, 1997, pp. 15-67. doi:10.1115/1.3101682
- H. W. Lord and Y. Shulman, “A Generalized Dynamical Theory of Thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No.5, 1967, pp. 299-309. doi:10.1016/0022-5096(67)90024-5
- S. Kaliski, “Wave Equations of Thermoelasticity,” Bulletin of the Polish Academy of Sciences Technology, Vol. 13, 1965, pp. 253-260.
- H. M. Youssef, “Fractional Order Generalized Thermoelasticity,” Journal of Heat Transfer, Vol. 132 No. 6, 2010. doi:10.1115/1.4000705
- H. M. Youssef, “Generalized Thermoelastic Infinite Medium with Cylindrical Cavity Subjected to Moving Heat Source,” Mechanics Research Communications, Vol. 36, No. 4, 2009, pp. 487-496. doi:10.1016/j.mechrescom. 2008.12.004
- G. Hanig and U. Hirdes, “A Method for the Numerical Inversion of Laplace Transform,” Journal of Computational and Applied Mathematics, Vol. 10, No. 1, 1984, pp. 113-132. doi:10.1016/0377-0427(84)90075-X

