Intelligent Control and Automation
Vol.5 No.2(2014), Article
ID:46300,9
pages
DOI:10.4236/ica.2014.52008
A Method for Automating Signal Analysis from Therapeutic Devices
Mohammed A. Eslami, Joshua W. Guag
Division of Physics, Office of Science and Engineering Laboratories, Center for Devices and Radiological Health, Food and Drug Administration, Silver Spring, USA
Email: mohammed.eslami@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 March 2014; revised 22 April 2014; accepted 29 April 2014
ABSTRACT
Many methods exist for cardiac and neural signal feature extraction and identification, but a published method for validation of therapeutic medical devices by computer analysis of their signals can be seldom found. This paper presents a simple, fast algorithm to extract the electrical stimulation including pulse width, exponential decay, and time between pulses from neurostimulators, pacemakers, implantable cardioverter defibrillators (ICDs), and transcutaneous electric nerve stimulators (TENS). An experimental validation demonstrated the automated analysis provide means to expedite device validation testing. In the future studies, the algorithm should be improved for its robustness and checked for analysis of signals with lower SNR. A figure of merit is provided to expedite electromagnetic compatibility (EMC) tests on the devices to ensure proper operation in the presence of electromagnetic emitters.
Keywords:Medical Devices, Electromagnetic Compatibility, Signal Analysis

1. Introduction
The emergence of many therapeutic medical devices such as pacemakers and neurostimulators brings with it a need to automate a test to monitor the output signal of the medical device for any anomalies. It is important to confirm that each device manufactured is working properly before packaging it and having it enter the market. By the automation of monitoring of the signal from the therapeutic device this validation testing can be expedited. A figure of merit that includes a score that is based on deformations in the pulses―such as change in pulse width, inter-pulse time, and shape of the waveform―and missing pulses can ensure that each manufactured device is operating properly.
Much work has been done to separate cardiac signals into their respective parts from long ambulatory signals [1] -[3] . In cardiac signal detection there is a focus to develop algorithms that can quickly analyze the data. Johannesson and Paleonetti [1] use the U3 algorithm [2] [4] to mark QRS complexes as acceptable or unacceptable. An automated method using this algorithm was shown to score these complexes comparable to that of an observer monitoring the QRS signal. U.S. Patent 7970472 was the most recent source that was found in detecting a pacing system malfunction from a pacemaker, and looked into the cause of the detected malfunction, and displaying the detected malfunction along with its cause [5] . [3] [6] published by the same author of the patent uses a finite state machine developed to identify pulses by their unique morphology and reject noise artifacts by measuring and qualifying the leading edge, trailing edge, pulse amplitude, pulse width, and a count of the significant slopes that surround the pacemaker pulse.
In this paper, the U3 function is used to analyze outputs from selected therapeutic devices and compare them to a baseline measurement for detection of anomalies. The output signal from pacemakers, implantable cardioverter defibrillators (ICDs), and neurostimulators produce pulses that leave no net charge from the stimulation and can be modeled with exponential curves during the duration of a pulse. This work was specifically motivated to automate electromagnetic compatibility (EMC) tests for detection of anomalies within the signal of a therapeutic device. For this paper, the U3 algorithm is used to determine any change in pulse widths, exponential decays, and inter-pulse times of pulses within a 15 second window of the signal measured while a therapeutic device is exposed to electromagnetic fields. Pulse width is defined as the time the pulse is above the noise level, while inter-pulse time is the time from the trailing edge of the current pulse to the leading edge of the next pulse. The exponential decay is the decay factor that is extrapolated by fitting an exponential function to a single pulse within the signal. The rest of this paper is organized as follows: Section 2 describes the background behind the U3 function and its use in the detection of specific features of pulses from a therapeutic device; Section 3 presents an experimental setup to test these therapeutic devices and the results of using the automated test setup; and the conclusions are in Section 4.
2. Mathematical Formulation
2.1. U3 Function
The U3 function is a non-linear operator that is a two-sided difference equation. It can be characterized by two parameters: 1) the lateral size window (k)―this is the spacing between the samples whose difference is found, and 2) the size of its central window (N)―which is the spacing between the two side differences that were found from the lateral size window. A diagram of the samples of interest that are retrieved from the input signal to use in the U3 function is shown in Figure 1, where i is the index of the input signal, N = 2m is the size of the central window for given m ≥ 2, and k is the size of the lateral window, where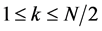 .
.
After the samples of interest are retrieved from the input signal using the block diagram in Figure 1, the U3 functionat sample i is given in Equation (1) for an input signal x(n).
 (1)
(1)
Geometrically, the U3 function finds the length of the secant line that connects the samples retrieved from lateral window. Using the U3 function, the output signal y(n) evaluated at the ith sample is given by the recursive function shown in Equation (2), where y(0) = 0.

Figure 1. A block diagram of the U3 function with central size window N and lateral size window k. This block is placed at the ith sample of an input signal x(n), and the blocks highlight the samples from the input signal that will be used in Equation (1).
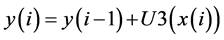 (2)
(2)
It can be seen from Equation (1) that so long as the central window size is smaller than the width of a pulse, the rightmost lateral window will not reach the next discontinuity until the left most lateral window has completed its operation on the current discontinuity. In addition, in areas where there is not much transition between the samples, such as the continuous parts of the signal, the U3 function has very little effect on the output signal y(i). The noise of the input signal has also been minimized because of its small transitions.
For a given input signal from one of the aforementioned therapeutic devices, the output signalis a train of pulses of width N whose rising edge occurs when the right lateral window coincides with the discontinuity, and falling edge occurs when the left lateral window coincides with the discontinuity. The number of pulses in the output signal is equal to the number of discontinuities of the input signal. It should be further noted that if the lateral window size is set so that k = 1, then the U3 function is a backward implementation of squared derivatives, and thus can be thought of as very high-pass filters. These high-pass filters then filter out everything but the discontinuities within the signal, and thus identify the beginning and trailing edges of each pulse.
The U3 algorithm requires less computational recourses than other signal analysis methods such as Fourier transform and wavelet analysis, and reduces the time required for the data analysis and the testing. The algorithm is simple and can be implemented with information of the medical device output signal characteristics including pulse rate, number of outputs, and rise and fall time of the signal and varying k and N parameters of the algorithm. The algorithm runs in linear time, O(N), where N is the number of samples in the signal, rather than the those required by finding the Fourier Transform, . This makes it a great candidate for testing of continuous operation of medical devices under a large number of conditions.
. This makes it a great candidate for testing of continuous operation of medical devices under a large number of conditions.
2.2. Test Implementation
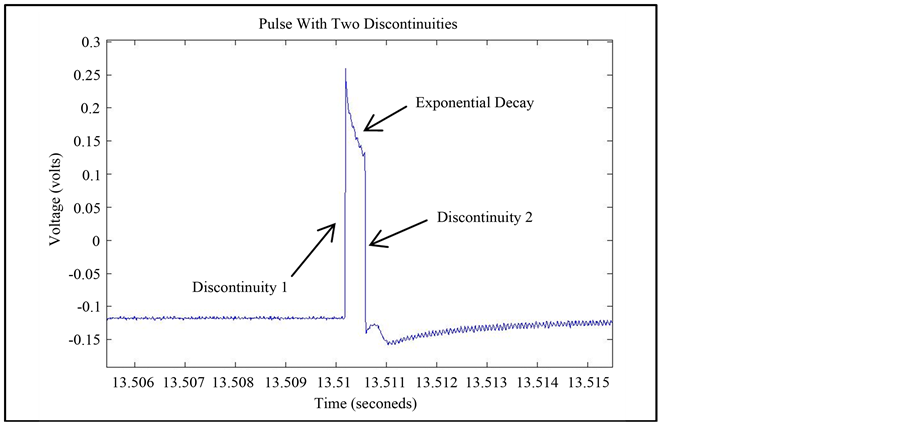
Signals from various therapeutic devices are first analyzed to identify features that could be used to identify a pulse within the input signal. Comparing 30 pulses that will be used as the input to the U3 function from different pacemakers, neurostimulators, ICDs, and TENS devices, it was determined that there are two types: 1) Pulse with two discontinuities and 2) Pulse with three discontinuities, as shown in Figure 2. The discontinuities that are identified within the signal and the known pulse period are used to extract the pulse width, exponential decay, and inter-pulse time.
A complete flowchart of the testing procedure is shown in Figure 3 and was implemented using MATLAB. The sampled signal from the medical device, s(n), is first passed to the recursive function Equation (2) that was described in the previous section.
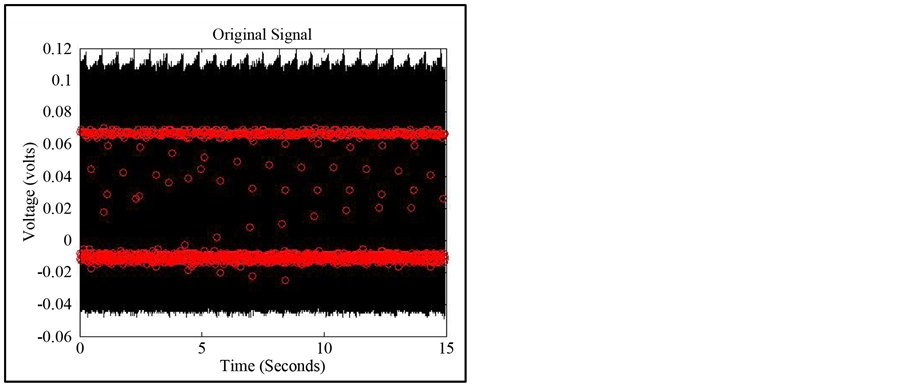
An adaptive threshold is applied to the output of the recursive function in Equation (2), to find the peaks (left column of Figure 4). The adaptive threshold to identify a peak is to be two standard deviations above the noise floor measured within the signal. This identifies the locations of all of the discontinuities within the signal. In other words, if this was a baseline signal, where there are no expected anomalies and everything is working properly, the locations extracted are the locations of the leading and trailing edges of each pulse. The algorithm assumes the information of the basic characteristics of the output signal such as pulse width, pulse period, and number of the pulses for each delivery of therapy (e.g., device with single vs. three outputs) of the medical devices is available for the baseline analysis. If sampling of the therapeutic device output signal has begun too early or too late, then the beginning and/or the end of the signal, s(n), will contain information from only a portion of a pulse. These portions must be filtered out from the data before checking for anomalies. This is accomplished by checking to see if the spacing between discontinuities is on the order of the pulse period within the first and last sampling periods of the signal. That is, the first and last periods of the output signal from Equation (2) are extracted. Next, the spacing between the discontinuities is identified within the first and last period. If the spacing is on the order of a programmed pulse period, then the pulse is marked as one with missing information and is removed.
The next step is to determine whether the pulse has two or three discontinuities. This can be expressed in terms of f, the operating frequency or number of pulses per second, T, the total time the signal was sampled, and Npeaks, the number of peaks detected and is given in Equation (3).
 (3)
(3)
 (a)
(a) (b)
(b)
Figure 2. Different pulse categories for medical devices having (a) two and (b) three discontinuities. The discontinuity locations and exponential decays are the features that will be extracted.
NDiscontinuity is checked to ensure that it is either two or three. If the device is effected by the exposure and part of a pulse is inhibited―for instance, if the third discontinuity of a pulse with three discontinuities is inhibited― then this number will not be recognized as a valid value since it will not be two or three. It is clear that during baseline measurements, this number will always be valid, i.e. either two or three, and that was indeed observed during the experiments. It should be noted that a device can either output a two-discontinuity pulse or a threediscontinuity pulse. The two will never mix together and still be a valid signal. In other words, if a two discontinuity pulse is detected within a three-discontinuity pulse signal, the signal will be marked as effected by the exposure.
If the measurement is a baseline measurement, the output signal from Equation (2) is used to determine the mean of the pulse width and inter-pulse time of a 15 second measurement. The exponential decay is found by corresponding the output signal from Equation (2) to the original signal (right column of Figure 4). The samples from the original signal are then used to find the best fit exponential function using least squares method for
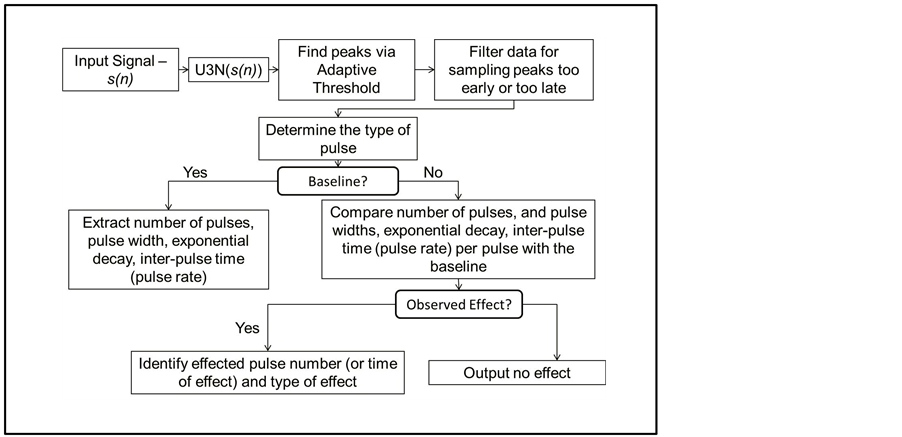
Figure 3. Test analysis flowchart.
 (a)
(a)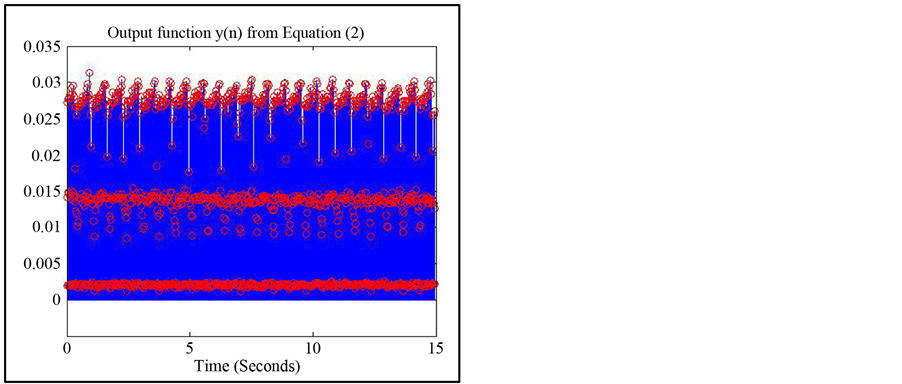 (b)
(b)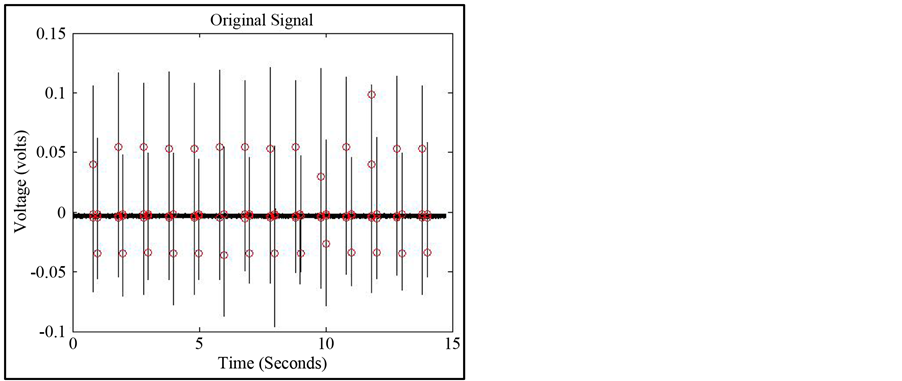 (c)
(c)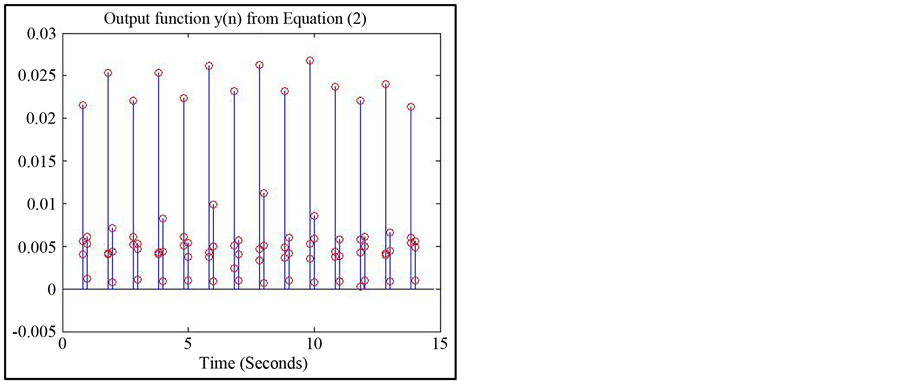 (d)
(d)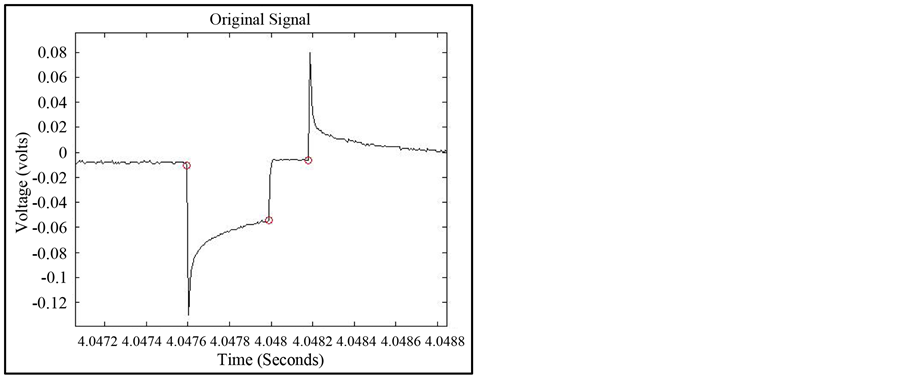 (e)
(e) (f)
(f)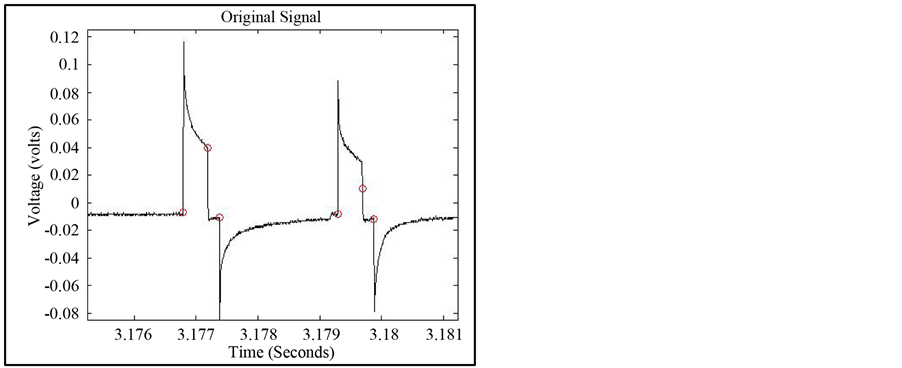 (g)
(g) (h)
(h)
Figure 4. Extracted pulses from (a)-(b): Neurostimulators over 15 seconds with 30 Hz pulse rate (c)-(d): Single Chamber Pacemaker (e)-(f) first pulse of a three chamber ICD and (g)-(h): second and third pulse of a three chamber ICD. Left column shows the U3N algorithm and the right column shows the features extracted from the original signal.
each pulse in the 15 second signal. The mean value of the exponential decay of all the pulses within the 15 second interval is found and stored with the pulse width and inter-pulse time. These values are stored for a 15 second sample of the signal.
If it is not a baseline measurement and NDiscontinuity is valid, then after the properties of each pulse are extracted from the signal, they are compared to the stored baseline measurement. In other words, the pulse width, exponential decay, and inter-pulse time that was extracted from the signal, are compared to the baseline measurements. If these parameters are larger than one standard deviation, which was chosen based on empirical measurements, from the stored baseline measurements, then the signal is marked as an affected signal.
3. Measurements and Results
3.1. Baseline Measurements
The success of this method depends on extracting the baseline measurements without any field exposure accurately. In addition, the parameters must converge within a 15 second window so as to be able to make the appropriate comparisons.
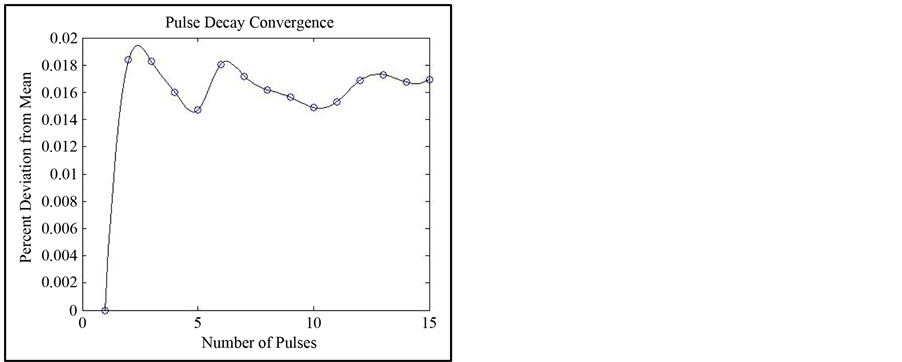
The output of the recursive function Equation (2), and the corresponding features extracted from the original pulses are shown in Figure 4. Figure 5 shows the convergence of the parameters well under 15 pulses for a device operating at 1 Hz. The other devices tested showed similar results and are listed in Table 1.
It can be seen that there is a rather large difference in scale on the y-axis between Figures 5(a)-(c). This is due to the fact that the sampling time is on the order of 6 μs which is on the order of the pulse width―450 μs. The pulse rate was three orders of magnitude larger at 1 s and microsecond deviations do not show as large an effect.
3.2. Devices Tested
Data from a security system simulator designed at the FDA [7] [8] for EMC tests on therapeutic devices were used to test the algorithm. Table 2 lists a summary of devices that were tested in the presence of electromagnetic radiation at various modulations and carrier frequencies. The output signal from total 14 sample medical devices was tested using the U3 algorithm. The medical device output signals used in the study were recorded for 15 seconds period with 150 kHz sampling rate. The table lists the type of device, namely a pacemaker, neurostimulator, ICD, or TENS, the rate the device would send output pulses, and the number of those devices tested at that rate. An operator observed the output signal of the medical device, which is shown in the “Observed Effects” column of Table 2 and compared that to automated labeling presented by the algorithm, shown in the “Detected Effects” column of Table 2. Data from the previous studies [7] showed EMI effects could either inhibit pulses or add extraneous noise pulses to the signal. Therefore, these were the two primary effects that were used as test data for various medical devices. Some of the effects were simulated by manipulating baseline data to see if the algorithm could detect the effect accordingly.
 (a)
(a)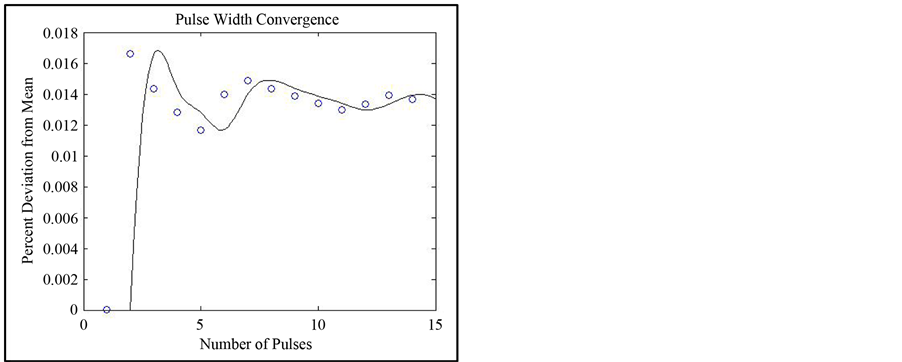 (b)
(b)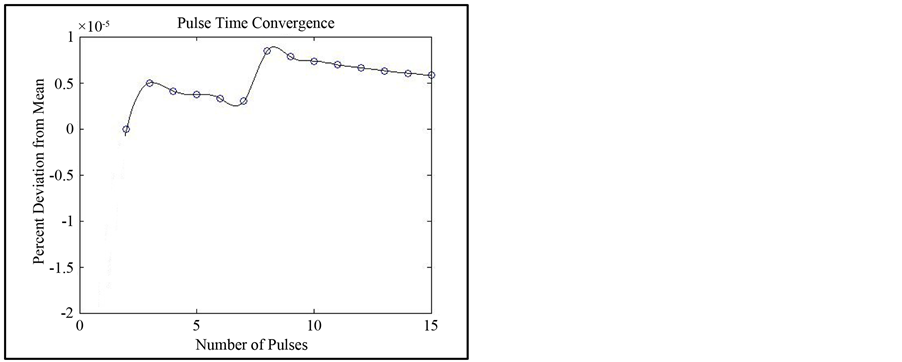 (c)
(c)
Figure 5. Convergence of the algorithm versus number of pulses for pulse (a) width (b) exponential decay and (c) interpulse time.
Table 1. Summary of parameters extracted from various devices tested.
*Device with single output (single pulse) per delivery of therapy; **device with three output (three pulses) per delivery of therapy.
Table 2. Summary of results tested for medical devices in the presence of an interferer.
*Indicates simulated data was used; **indicates false positives detected by algorithm.
The results show that the algorithm performs as well as an observer in identifying effected signals. However, at times, the output of the U3 produced a “long peak,” which is a wide valley rather than a sharp peak at one of the discontinuities, and thus the peak detector could not correctly identify those peaks. These were false positives that were reported where the algorithm detected an effect when there was no effect. In these cases, the peak detector used could not identify some of the peaks from the U3 algorithm appropriately and thus NDiscontinuity was not a valid number and the signal was reported to be effected. The algorithm never failed to detect an effect, though it did report a few false positives. However, for the purpose of the device validation testing, this is considered acceptable due to the fact that if an effect within the signal is detected, the test needs to be checked for its repeatability.
4. Conclusions
This paper presented a fast, simple method for signal validation from electrically stimulating therapeutic devices using the U3 algorithm. The algorithm successfully detected discontinuities of a baseline measurement to extract the pulse width, exponential decay, and inter-pulse time of a signal. An interferer was then activated that could potentially cause an effect on the signal. The extracted features of the signal are compared to the known baseline measurements for detection of anomalies. This automated analysis enhances abilities to quickly record and analyze variations from the signal and reduces analysis time.
Currently, the algorithm is not robust in localizing the problem. Once the problem is detected, it ripples its effects through the rest of the signal. For instance, if a problem occurs in pulse 3, the analysis has this ripple effect through all pulses after pulse 3. This needs to be made more robust to properly localize anomalies. In addition, the technique needs to be checked against signals with lower SNRs to find the limit of their ability in detection of these anomalies. In addition, the various amplitudes of the pulses within the U3 algorithm could potentially be used to extract the exponential decay of each pulse. This would avoid saving the original signal in memory and all processing would take place straight on the fast, simple U3 output.
Acknowledgements
This project was supported in part by an appointment to the Research Participation Program at the Center for Devices and Radiological Health administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and the U.S. Food and Drug Administration.
References
- Johannesen, L. and Galeotti, L. (2012) Automatic ECG Quality Scoring Methodology: Mimicking Human Annotators. Physiological Measurement, 33, 1479-1489. http://dx.doi.org/10.1088/0967-3334/33/9/1479
- Paoletti M. and Marchesi, C. (2006) Discovering Dangerous Patterns in Long-Term Ambulatory ECG Recordings Using a Fast QRS Detection Algorithm and Explorative Data Analysis. Computer Methods and Programs in Biomedicine, 82, 20-30. http://dx.doi.org/10.1016/j.cmpb.2006.01.005
- Ricke A.D., Swiryn, S., Bauernfeind, R.A., Conner, J.A., Young, B. and Rowlandson, G.I. (2011) Improved Pacemaker Pulse Detection: Clinical Evaluation of a New High-Bandwidth Electrocardiographic System. Journal of Electrocardiology, 2, 265-274. http://dx.doi.org/10.1016/j.jelectrocard.2010.09.008
- Marchesi C. and Paoletti, M. (2004) ECG Processing Algorithms for Portable Monitoring Units. Internet Journal of Medical Technology, 1, 23.
- Ricke, A. and Rowlandson, G.I. (2010) Module and Device for Discerning Therapeutic Signals from Noise in Physiological Data. US PTO: 20100317982.
- Ricke A.D., Swiryn, S., Sahakian, A.V., Petrutiu, S., Young, B. and Rowlandson, G.I. (2008) The Relationship between Programmed Pacemaker Pulse Amplitude and the Surface Electrocardiogram Recorded Amplitude: Application of a New High-Bandwidth Electrocardiogram System. Journal of Electrocardiology, 41, 526-530. http://dx.doi.org/10.1016/j.jelectrocard.2008.06.023
- Seidman S.J., Brockman, R., Lewis, B.M., Guag, J, Shein, M.J., Clement, W.J., Kippola, J., Digby, D., Barber, C. and Huntwork, D. (2010) In Vitro Tests Reveal Sample Radiofrequency Identification Readers Inducing Clinically Significant Electromagnetic Interference to Implantable Pacemakers and Implantable Cardioverter-Defibrillators. Heart Rhythm, 1, 99-107. http://dx.doi.org/10.1016/j.hrthm.2009.09.071
- Witters, D., Bassen, H., Guag, J., Addissie B., LaSorte, N. and Rafai, H. (2013) Assessment of Risks of Electromagnetic Interference for Personal Medical Electronic Devices (PMEDs) from Emissions of Millimeter Wave Security Screen Systems. Proceedings SPIE Defense, Security, and Sensing, Baltimore, 8711.


