Journal of Information Security
Vol.5 No.3(2014), Article
ID:48057,9
pages
DOI:10.4236/jis.2014.53011
I-PRESENTTM: An Involutive Lightweight Block Cipher
Muhammad Reza Z’aba1, Norziana Jamil2, Mohd Ezanee Rusli2, Md. Zaini Jamaludin2, Ahmad Azlan Mohd Yasir3
1MIMOS Berhad, Kuala Lumpur, Malaysia
2College of Information Technology, Universiti Tenaga Nasional, Kajang, Malaysia
3CoRE Expert Systems Sdn. Bhd. Office 1, Level 2, Resource Centre, Technology Park Malaysia, Kuala Lumpur, Malaysia
Email: reza.zaba@mimos.my, norziana@uniten.edu.my, ezanee@uniten.edu.my, mdzaini@uniten.edu.my, drazlan@core-xs.com,
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 May 2014; revised 15 June 2014; accepted 11 July 2014
ABSTRACT
This paper proposes a new involutive light-weight block cipher for resource-constraint environments called I-PRESENTTM. The design is based on the Present block cipher which is included in the ISO/IEC 29192 standard on lightweight cryptography. The advantage of I-PRESENTTM is that the cipher is involutive such that the encryption circuit is identical to decryption. This is an advantage for environments which require the implementation of both circuits. The area requirement of I-PRESENTTM compares reasonably well with other similar ciphers such as PRINCE.
Keywords:Block Cipher, Lightweight Cryptography, PRESENT, PRINCE, Cryptanalysis

1. Introduction
In recent years, there is a steady rise in the research into lightweight cryptography, i.e. cryptography suitable for implementation in resource-constrained environments. The constraints on the resources include compact implementation area, small memory and low power consumption in devices such as RFID tags and wireless sensor nodes. The need arises because traditional cryptography cannot fit into these environments due to the relatively high implementation costs.
In this paper, the focus is on lightweight block ciphers. There are numerous existing proposals which include PRESENT [1] , the KATAN and KTANTAN families [2] , LBlock [3] , LED [4] , PRINCE [5] , and the Simon and Speck families [6] , the last of which was proposed by the United States National Security Agency (NSA). They were developed to address the need for dedicated ciphers to be used in resource-constrained environments for which the general purpose Advanced Encryption Standard (AES) block cipher [7] was unsuitable. With the exception of PRINCE, all of these ciphers require different circuits for encryption and decryption. Therefore, two circuits have to be implemented in order to perform these operations which add to the implementation cost. Our cipher proposed in this paper, on the other hand, requires only a single circuit to perform these operations.
As recognition for the need for interoperability, the block ciphers PRESENT and CLEFIA [8] have been included in the ISO/IEC 29192 standard on lightweight cryptography. The standard specifies the minimum security level at 80 bits (i.e. the key size). To be included in this standard, the hardware and software implementation properties of the cipher should have advantage over existing ISO standards such as ISO/IEC 18033 (encryption algorithms), ISO/IEC 9798 (entity authentication) and ISO/IEC 11770 (key management).
In this paper, we propose a new lightweight block cipher. Our cipher, called I-PRESENTTM, is an involution in the sense that the encryption and decryption circuits are identical. This translates into a smaller implementation cost compared to other existing lightweight block ciphers which require separate circuits to perform encryption and decryption. Our cipher is based on present and the involutive part is inspired by PRINCE. To the best of our knowledge, the only other involutive lightweight block ciphers proposed are LBlock and PRINCE.
This paper is organized as follows. In Section 2, we give a description of our cipher. The design rationale is explained in Section 3 and Section 4 outlines the security analysis on the cipher. The implementation analysis is presented in Section 5. A summary and the conclusion for the paper are given in Section 6.
2. Description of I-PRESENTTM
I-PRESENTTM accepts a 64-bit plaintext block and master key lengths of 80 and 128 bits. These variants are denoted as I-PRESENT-80 and I-PRESENT-128, respectively. The master key is used by the key scheduling algorithm (key schedule) as input to produce a set of thirty 64-bit round subkeys. The ciphertext block is generated after applying a round function 15 times to the plaintext block, followed by an involutive function and another 15 applications of the inverse round function. In total, the number of rounds for the cipher is 30.
2.1. Encryption
The encryption function takes as input a 64-bit plaintext state and a set of thirty-two 64-bit round subkeys. The values for subkey are produced by the key schedule which will be described later in Section 2.4. Encryption proceeds by iterating a round function 15 times which consists of a key mixing transformation MixKey, a nonlinear transformation STrans and a bit permutation PTrans.
This is followed by the application of a function Invo and iterating the inverse round function 15 times to state. The current value of state is output as the ciphertext. This process is given in Listing 1.1 and illustrated in Figure 1.
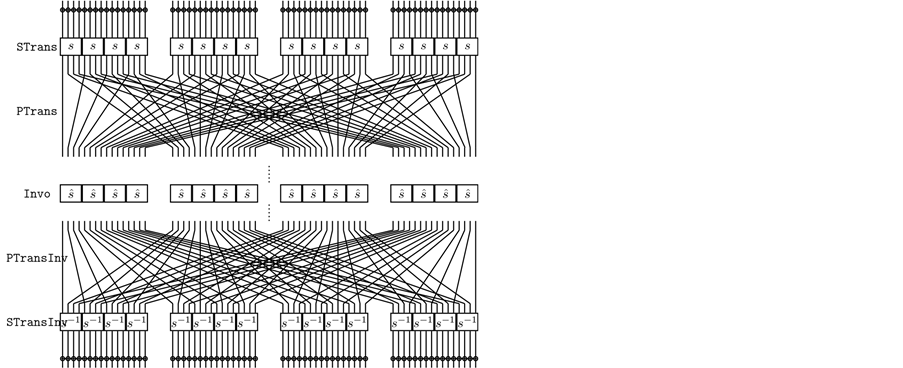
Figure 1. I-PRESENTTM block cipher.
2.2. Decryption
The decryption function takes as input a 64-bit ciphertext state and a set of thirty 64-bit round subkeys subkey. The values for subkey are produced by the key schedule which will be described later in Section 2.4. Decryption is identical to encryption, i.e. the same as Listing 1.1, except that the round subkeys are used in the reverse order. Therefore, subkey [0] in decryption is subkey [31] in encryption, subkey [1] in decryption is subkey [30] in encryption and so on.

2.3. Round Function Transformations
This section describes the transformations used in the round function of I-PRESENTTM.
The Function MixKey. MixKey takes the current value of state and XOR its value with the value of the current round subkey.
The Functions STrans and STransInv. STrans and STransInv both divide the input state into sixteen 4-bit words and applies a 4 × 4 s-box simultaneously to each word. A 4 × 4 s-box is a nonlinear function that maps a 4-bit input to a 4-bit output.
The mapping of the s-box used in I-PRESENTTM is given in Table 1 where the values given are in hexadecimal. The s-box s is used in STrans and its inverse, s−1 is used in decryption. A 4-bit input x = 1 to an s-box s would give an output of s(1) = 6. If x = 6 is used as input to its inverse s−1, then the output is s−1(6) = 1.
The Functions PTrans and PTransInv. The function PTrans performs a bit permutation on its 64-bit input state and updates the value of the state with the permuted value. Let 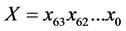 and
and 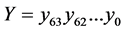 denote the 64-bit input and output state of PTrans, respectively where bit number 63 is the leftmost bit of the state, bit 62 is the second leftmost bit of the state and so on. The permutation in PTrans can be described by Table2
denote the 64-bit input and output state of PTrans, respectively where bit number 63 is the leftmost bit of the state, bit 62 is the second leftmost bit of the state and so on. The permutation in PTrans can be described by Table2
Table 1. The s-box s and its inverse s−1 used in I-PRESENTTM.
The permutation states that the bit in position i is moved to position P(i). For instance, bit x0 is unchanged and bit x1 is moved to position 16 and the output state Y is updated as follows.
The Function Invo. Invo divides the 64-bit input state into sixteen 4-bit words and applies a 4 × 4 s-box sˆ simultaneously to each word. The mapping for sˆ is given in Table3
2.4. Key Schedule
I-PRESENTTM supports two key sizes: 80 and 128 bits. The key schedule for these key lengths is the same as used in PRESENT. For completeness, we include the description of the key schedules in this section.
80-bit Key. The 80-bit key is stored in register K and represented as k79k78 ...k0. The subkey for round i, i.e. Ki = κ63κ62 ...κ0 is derived from the 64 left-most bit of the current register K:
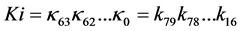
In the first round, subkey K0 is derived directly from the 64 left-most bit of the master key. After this key is extracted, the current register K = k79k78 ...k0 is updated as follows where the value i is initialized to 1, i.e. i = 1.
1) Rotate the register K by 53 bits to the left:
2) 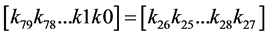
3) Apply the s-box s' to the four left-most bit of the register K:
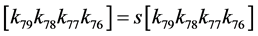
where the mapping for s is given in Table1
4) XOR bits k19k18k17k16k15 with a roundcounter i where the right-most bit is the least significant bit:
5) 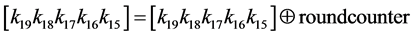
6) Extract the ith subkey as 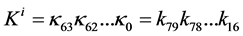 and increment the value of i by one.
and increment the value of i by one.
The above steps are repeated until all round subkeys are derived, i.e. until K31 is derived.
128-bit Key. The 128-bit key is stored in register K and represented as k127k126 ...k0. The subkey for round i, i.e. 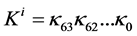 is derived from the 64 left-most bit of the current register K:
is derived from the 64 left-most bit of the current register K:
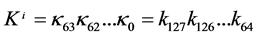
In the first round, subkey K0 is derived directly from the 64 left-most bit of the master key. After this key is extracted, the current register 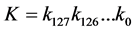 is updated as follows where the value i is initialized to 1, i.e. i = 1.
is updated as follows where the value i is initialized to 1, i.e. i = 1.
1) Rotate the register K by 53 bits to the left:
2) 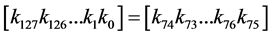
3) Apply the s'-box s to the eight left-most bit of the register K:
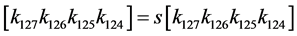
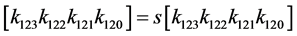
where the mapping for s is given in Table1
4) XOR bits k67k66k65k64k63 with a round counter i where the right-most bit is the least significant bit:
5) 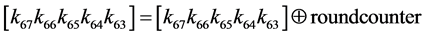
6) Extract the ith subkey as 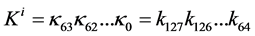 and increment the value of i by one.
and increment the value of i by one.
The above steps are repeated until all round subkeys are derived, i.e. until K31 is derived.
3. Design Rationale
3.1. The Nonlinear Layers
The basis of the construction of the s-box of I-PRESENTTM is the same as P’s s-box [1] . One of the main criteria in the design of PRESENT’s s-box is that there is no 1-bit input difference that results in a 1-bit output difference. This is to prevent the propagation of trivial differential trails due to the use of a bit permutation. Other sboxes that have this criterion are the eight s-boxes of the block cipher Serpent [9] .
The involutive s-box used in the function Invo is the same s-box used in the block cipher Noekeon [10] . According to Liu et al. [11] , there always exists a 1-bit input difference which results in a 1-bit output difference for a 4 × 4 involutive s-box. As a consequence, it does not meet the criteria for the I-PRESENTTM’s s-box. However, since this s-box is proposed to be used only in the middle of the cipher, we expect the security of the new construction is similar if not superior to PRESENT.
3.2. The Permutation Layers
The bit permutation used in I-PRESENTTM is the same used in present. There is very little or no extra cost incurred when using bit permutation in hardware. However, higher cost will be incurred when implementing this operation in software. This is due to the extra operations (e.g. masking of bits, rotation) required to extract bits in specific positions in a word. The choice of bit permutation allows the designer of PRESENT to derive bounds on the resistance of the cipher against differential cryptanalysis (more in Section 4.1). I-PRESENTTM therefore inherits this property.
3.3. The Structure
I-PRESENTTM is an involutive cipher in the sense that the circuit for decryption is the same as for encryption. The only difference is the order of the round subkeys. The involutive part is inspired by the lightweight block cipher PRINCE [5] . The main advantage of this design is that only a single circuit is required to be implemented in environments which require both encryption and decryption. This substantially reduces the implementation cost if compared to a cipher with different circuits to perform these operations.
Note that it is possible to implement only the encryption circuit of a cipher but allows for encryption and decryption of arbitrary messages. For instance, in the counter mode (CTR), only the encryption circuit of a cipher is required to perform encryption and decryption of messages. In other modes such as cipher block chaining (CBC), we require both encryption and decryption circuits to perform the same operations.
In essence, an involutive function I connects two (not necessarily be involution) functions F and F−1 (the inverse of F), i.e. F−1 ∘I ∘F. This differs to the strategy used by other involutive ciphers such as Noekeon [10] , Khazad [12] and Anubis [13] where all its functions are required to be an involution.
As mentioned in Section 3.1, the use of a non-involutive s-box in the outer rounds allows a 1-bit input difference to trigger at least a 2-bit output difference. If we use an involutive s-box, it is possible for a 1-bit input difference to cause a 1 bit output difference [11] . This is an advantage to an attacker since a differential trail involving a small number of active s-boxes may be constructed.
4. Cryptanalysis
This section presents the security evaluation of I-PRESENTTM. The two most important attacks that a cipher should resist is differential [14] [15] and linear cryptanalysis [16] .
4.1. Differential and Linear Cryptanalysis
To gauge the resistant of I-PRESENTTM against differential cryptanalysis, we adopted the number of active s-boxes approach. This technique is used in many ciphers including the Advanced Encryption Standard (AES) [17] (Section 9) and CLEFIA, a cipher developed by Sony Corporation [18] (Section 2.1).
Let pˆ denote the probability of a differential trail and let N denote the block length of a cipher in bits. A key recovery attack requires roughly pˆ−1 chosen plaintexts and should not exceed the plaintext space, i.e. pˆ−1 < 2N. Let pmax denote the maximum differential probability of the s-box and na denote the number of active s-boxes. In order to resist differential cryptanalysis, na should be bounded by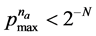 .
.
Based on the analysis done on PRESENT [1] (Theorem 1), it is known that any five-round differential trail has a minimum of 10 active s-boxes. The maximum differential probability of all I-PRESENTTM s-boxes is 2−2. For I-PRESENTTM, (2−2)na < 2−64 and so the cipher should have at least na = 32 active s-boxes in a differential trail.
If we ignore the Invo function, the probability of a 20-round differential trail is bounded by (2−2)4×10 = 2−80. A key recovery attack is not possible since the required number of chosen plaintexts exceed the plaintext space, i.e. 280 > 264. Since I-PRESENTTM has 30 rounds, we believe that the cipher provides ample protection against differential cryptanalysis.
Linear cryptanalysis is related to differential cryptanalysis [19] [20] . According to Bogdanov and Shibutani [21] , we can assume that the resistance of a cipher against both differential and linear cryptanalysis using the number of active s-boxes method to be the same. Therefore, based on our previous analysis on differential cryptanalysis, I-PRESENTTM is resistant to linear cryptanalysis.
4.2. Boomerang Cryptanalysis
In a nutshell, the boomerang attack [22] requires the construction of four differential trails. The cipher is considered as two halves where two differentials cover the upper half and the remaining two covers the lower half. Let p and q denote the probability of the differentials for the upper and lower halves, respectively. A valid distinguisher must satisfy (pq)2 > 2−N.
A 10-round boomerang distinguisher can be constructed by using two 5-round differential trails. Each trail has probability p = q = (2−2)10 = 2−20. So the total probability of this 10-round distinguisher is (2−20 × 2−20)2 = 2−80. This is much lower than 2−64 and thus, the full-round I-PRESENTTM is resistant to boomerang cryptanalysis.
4.3. Integral Cryptanalysis
Traditionally, integral cryptanalysis [23] is not well-suited to be applied on bit-based block ciphers such as I-PRESENTTM and PRESENT. However, by carefully inspecting the propagation of the inputs, the attack is still possible to be applied [24] . The best known integral attack on PRESENT is on 10 rounds [25] which is much less than the total number of rounds of present. Due to the similarity of I-PRESENTTM and PRESENT, we expect our cipher to be resistant to integral cryptanalysis.
4.4. Statistical Saturation
The statistical saturation attack exploits poor diffusion properties of a cipher [26] . It fixes certain bits in the plaintext and the distribution of certain bits of the ciphertext is observed. If the distribution is non-uniform, then the cipher is vulnerable to this attack. The attack managed to break 24 rounds of PRESENT using about 260 chosen plaintexts and 228 operations. Since I-PRESENTTM uses the same diffusion as PRESENT, the same analysis can be similarly be applied to I-PRESENTTM. However, since our cipher employs the function Invo in the middle of the cipher, we believe it will provide resistance to this attack.
5. Implementation
Table 4 gives an estimate on the area requirement for I-PRESENT-80TM in terms of the number of gate equivalents (GE). The estimation is based on the results obtained for PRESENT [1] (Section 6). The only major difference between the implementation of I-PRESENTTM and PRESENT is in the s-box layer. In I-PRESENTTM, we additionally use two 4 × 4 s-boxes 16 times.
Based on the estimation, one bit requires about 6 GE to store. The data and key state occupy 64 and 80 bits, respectively. This gives 384.39 GE and 480.49 GE to the implementation cost. In PRESENT, the cost for a single 4 × 4 s-box is about 28.028125 GE. In I-PRESENTTM, we use three different s-boxes each repeated 16 times. Therefore, 28.028125 × 3 × 16 = 1345.35 GE is required to implement the s-boxes. To obtain a more precise implementation result, specific hardware tools such as Mentor Graphics Modelsim and Synopsis Design Compiler can be used for simulation and synthesis, respectively. The estimation is part of the evaluation for a lightweight block cipher and is performed on existing ciphers such as PRESENT.
A comparison between the implementation of related lightweight block ciphers is given in Table5 Note that although PRESENT requires 1570 GE in the 80-bit security level, the implementation is only for encrypt-only while our implementation is for both encryption and decryption. LBlock is included in the comparison since the
Table 5. Comparison of existing implementation of related lightweight block ciphers.
cipher can also be considered as an involution. The implementation cost for LBlock [3] is lower compared to our cipher because LBlock employs the Feistel network [27] while ours is a substitution-permutation network (SPN) type of cipher. The cost to implement I-PRESENTTM is still reasonable since another SPN-type cipher, KLEIN [28] , requires more physical space than ours.
In the 128-bit key space, I-PRESENTTM requires much less GE compared to PRINCE [5] . As mentioned earlier, the involution part of I-PRESENTTM is inspired by PRINCE and we managed to provide a lower implementation cost. KLEIN only supports key size up to 96 bits which require 2769 GE. Our cipher supports a stronger key size (128 bits) and requires 2783 GE which is very close to the 96-bit key KLEIN. The description of the block ciphers included in the comparison in Table 5 can be found in their respective references. The interested reader may refer to the related documents for a detailed description of the block ciphers.
6. Conclusions
In this paper, we propose a new 64-bit block involutive lightweight block cipher called I-PRESENTTM. The main advantage of the cipher is that encryption and decryption can be performed using the same circuit, thus providing savings on implementation. This differs to many other existing lightweight block ciphers which require separate circuits to perform encryption and decryption. This adds to the implementation cost of these ciphers. In terms of area requirements, our cipher compares reasonably well with other 80-bit key lightweight block ciphers. It even outperforms PRINCE in the 128-bit key space, in which the idea of the involution for I-PPRESENTTM is based on.
As future work, we may simulate and synthesize I-PRESENTTM using appropriate tools. Further cryptanalysis may also be performed using more sophisticated attack techniques.
Acknowledgements
This work is a research collaboration with CoRE Expert System Sdn Bhd and it was sponsored by them and also Ministry of Education Malaysia, under Fundamental Research Grant Scheme 2014.
References
- Bogdanov, A., Knudsen, L.R., Leander, G., Paar, C., Poschmann, A., Robshaw, M.J.B., Seurin, Y. and Vikkelsoe, C. (2007) PRESENT: An Ultra-Lightweight Block Cipher. In: Paillier, P. and Verbauwhede, I., Eds., Cryptographic Hardware and Embedded Systems—CHES 2007, 9th International Workshop, Volume 4727 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 450-466.
- De Canni’ere, C., Dunkelman, O. and Knezevic, M. (2009) KATAN and KTANTAN—A Family of Small and Efficient Hardware-Oriented Block Ciphers. In: Clavier, C. and Gaj, K., Eds., Cryptographic Hardware and Embedded Systems—CHES 2009, 11th International Workshop, Volume 5747 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 272-288.
- Wu, W.L. and Zhang, L. (2011) LBlock: A Lightweight Block Cipher. In: Lopez, J. and Tsudik, G., Eds., Applied Cryptography and Network Security—9th International Conference, ACNS 2011, Volume 6715 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 327-344.
- Guo, J., Peyrin, T., Poschmann, A. and Robshaw, M. (2011) The LED Block Cipher. In: Preneel, B. and Takagi, T., Eds., Cryptographic Hardware and Embedded Systems—CHES 2011, 13th International Workshop, Volume 6917 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 326-341.
- Borghoff, J., Canteaut, A., Güneysu, T., Kavun, E.B., Knezevic, M., Knudsen, L.R., Leander, G., Nikov, V., Paar, C., Rechberger, C., Rombouts, P., Thomsen, S.S. and Yalcin, T. (2012) PRINCE: A Low-Latency Block Cipher for Pervasive Computing Applications. In: Wang, X.Y. and Sako, K., Eds., Advances in Cryptology—ASIACRYPT 2012 18th International Conference on the Theory and Application of Cryptology and Information Security, Volume 7658 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 208-225.
- Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B. and Wingers, L. (2013) The SIMON and SPECK Families of Lightweight Block Ciphers. Cryptology ePrint Archive, Report/404. http://eprint.iacr.org/2013/404/
- National Institute of Standards and Technology (2001) Advanced Encryption Standard. Federal Information Processing Standard (FIPS) 197. http://csrc.nist.gov/publications/fips/
- Sony Corporation (2007) The 128-Bit Blockcipher CLEFIA Algorithm Specification. http://www.sony.net/Products/cryptography/clefia/about/index.html
- Anderson, R., Biham, E. and Knudsen, L. (1998) Serpent: A Proposal for the Advanced Encryption Standard. NIST AES Proposal. http://www.cl.cam.ac.uk/~rja14/serpent.html
- Daemen, J., Peeters, M., Van Assche, G. and Rijmen. V. (2000) Nessie Proposal: NOEKEON. First Open NESSIE Workshop, November. http://gro.noekeon.org/
- Liu, B.Z., Gong, Z., Qiu, W.D. and Zheng, D. (2011) On the Security of 4-Bit Involutive S-Boxes for Lightweight Designs. In: Bao, F. and Weng, J., Eds., Information Security Practice and Experience—7th International Conference, ISPEC 2011, Volume 6672 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 247-256.
- Barreto, P.S.L.M. and Rijmen, V. (2000) The Khazad Legacy-Level Block Cipher. First Open NESSIE Workshop, November. https://www.cosic.esat.kuleuven.be/nessie/workshop/
- Barreto, P.S.L.M. and Rijmen, V. (2000) The Anubis Block Cipher. First Open NESSIE Workshop, November. https://www.cosic.esat.kuleuven.be/nessie/workshop/
- Biham, E. and Shamir, A. (1991) Differential Cryptanalysis of DES-Like Cryptosystems. Journal of Cryptology, 4, 3-72. http://dx.doi.org/10.1007/BF00630563
- Biham, E. and Shamir, A. (1993) Differential Cryptanalysis of the Data Encryption Standard. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-1-4613-9314-6
- Matsui, M. (1994) Linear Cryptanalysis Method for DES Cipher. In: Helleseth, T., Ed., Advances in Cryptology— EUROCRYPT ’93: Workshop on the Theory and Application of Cryptographic Techniques, Volume 765 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 386-397.
- Daemen, J. and Rijmen, V. (2002) The Design of Rijndael, AES—The Advanced Encryption Standard. Springer-Verlag, Berlin.
- Sony Corporation (2007) The 128-Bit Blockcipher CLEFIA Security and Performance Evaluations. http://www.sony.net/Products/cryptography/clefia/about/index.html
- Chabaud, F. and Vaudenay, S. (1995) Links between Differential and Linear Cryptanalysis. In: De Santis, A., Ed., Advances in Cryptology—EUROCRYPT ’94, Workshop on the Theory and Application of Cryptographic Techniques, Volume 950 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 356-365.
- Blondeau, C. and Nyberg, K. (2013) New Links between Differential and Linear Cryptanalysis. In: Johansson, T. and Nguyen, P.Q., Eds., Advances in Cryptology—Eurocrypt 2013: International Conference on the Theory and Application of Cryptographic Techniques, Volume 7881 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 388-404.
- Bogdanov, A. and Shibutani, K. (2012) Generalized Feistel Networks Revisited. Designs, Codes and Cryptography, 66, 75-97.
- Wagner, D. (1999) The Boomerang Attack. In: Knudsen, L., Ed., Fast Software Encryption: 6th International Workshop, FSE’99, Volume 1636 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 156-170.
- Knudsen, L. and Wagner, D. (2002) Integral Cryptanalysis. In: Daeman, J. and Rijmen, V., Eds., Fast Software Encryption: 9th International Workshop, FSE 2002, Volume 2365 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 112-127.
- Z’aba, M.R., Raddum, H., Henricksen, M. and Dawson, E. (2008) Bit-Pattern Based Integral Attack. In: Nyberg, K., Ed., Fast Software Encryption: 15th International Workshop, FSE 2008, Volume 5086 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 363-381.
- Wu, S.B. and Wang, M.S. (2013) Integral Attacks on Reduced-Round PRESENT. In: Qing, S.H., Zhou, J.Y. and Liu, D.M., Eds., Information and Communications Security, 15th International Conference, ICICS 2013, Volume 8233 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 331-345.
- Collard, B. and Standaert, F.-X. (2009) A Statistical Saturation Attack against the Block Cipher PRESENT. In: Fischlin, M., Ed., Topics in Cryptology—CT-RSA 2009, Volume 5473 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 195-210.
- Feistel, H. (1973) Cryptography and Computer Privacy. Scientific American, 228, 15-23. http://dx.doi.org/10.1038/scientificamerican0573-15
- Gong, Z., Nikova, S. and Law, Y.W. (2012) KLEIN: A New Family of Lightweight Block Ciphers. In: Juels, A. and Paar, C., Eds., RFID Security and Privacy—7th International Workshop, RFIDSec 2011, Volume 7055 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 1-18.


