Journal of Information Security
Vol. 3 No. 3 (2012) , Article ID: 21341 , 7 pages DOI:10.4236/jis.2012.33025
A New Steganography Method Based on the Complex Pixels
1Department of Information Technology, Tehran University, Kish, Iran
2Department of Information and Communication Technology, Malekeashtar University, Tehran, Iran
Email: amin_hashemi@ut.ac.ir, payandeh@mut.ac.ir
Received February 16, 2012; revised March 13, 2012; accepted May 2, 2012
Keywords: Steganography; Halftone; Fluyd Steinberg; Attacker; Steganalysis
ABSTRACT
Today steganography has attracted the attention of many researchers. In this paper, we propose a new steganography method for secure Data communication on half tone pictures. Using the halftone pictures improve the security and capacity. In this method, the complexity of every pixel in picture is computed, then a neibourhood is defined to compute the complexity of every pixel, and then the complexity of every pixel is computed in the neibourhood. Placing data in the monotonous areas of halftone can explain the presence of hidden data. A method has been represented that surveys the position of every pixel neibouring others and prevents including in monotonous areas. If that was a complicated one, steganography bit after stonehalf will be hidden after scrolling the whole, the process of spreading error will be done. Performing the suggested method improves the quality of placing picture and increases its security.
1. Introduction
Steganography has enjoyed a lot of importance since last decade. The Art of steganogeraphy has attracted human attention for many years. It is very important because disclosing a message even as encoded is dangerous many times. Steganography is a branch of hiding information. It contains a few branches as cryptography, Watermarking, Fingerprinting [1]. The stego medium that a hidden message is inserted in it is called cover medium. It may be a picture, a sound, and a film. After inserting a message by Algorithm containing, it is called placed medium span. The data that we insert in cover medium is secret message. The key which is used to insert message and take out secret message is called placing key. The techniques that help us to recognize cover medium and span are called disclosing [2]. When we disclose a secret, target is just to understand the hidden message, and we don’t observe the obligation to discover the contents of message. A method has been given to disclose halftone. They are vastly used in printing a book, magazine newspaper and computer printers. The pictures that have been saved by fax or pictures taken form pdf of some documents have the scanner format of printed texts include halftone. Changing the grey colour pictures into a two surface picture which its pixels range 0 - 255 (black and white) is called the process of making halftone. Generally, they are 3 groups [3] in the traditional method of halftone that is the oldest one, there are alternative arrays of threshold surfaces. The extent of light surface each of the pixels less than they should level is 0, and if it is more, it is changed to 255 [4]. In two surface process with blue noise, It is tried to insert the resulting noise of halftone in high frequencies [5]. The usage of the method is because the vision system of human is less sensitive to higher frequency noise in a picture. In binary direct search, it is tried some amount to be chosen for every pixel in halftone that will optimize the quality norm. The best quality among halftone methods is binary based search. There is different Algorithm for making halftone. One of the most important is fluyd Steinberg Algorithm that have been used here [6]. This Algorithm was published by Robert W. Fluyd and Luis Steinberg which is used for making changes [7]. For example, it changes a picture with GIF format with maximum 255 colours. In the mentioned method the light surface of every pixel is compared with threshold amount of 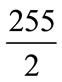 and if greater than threshold it is changed to 255 if smaller it is changed to 0 and so we can show every pixel with a bit. This change creates a little error in the new picture. This Algorithm for one pixel to its neibouring acts mutually with considering expansion distribution error. If it be the first pixel amount and its new value be 255, the error value equals e = 255 – F. In Fluyd Steinberg’s method the error value in neibouring pixels is like what is shown in Figure 1, Will spread the value of error with different weights between neibouring pixels spreads that are at the right side or under pixel. For example if the right side pixel value mentioned be A, the new value will be A +
and if greater than threshold it is changed to 255 if smaller it is changed to 0 and so we can show every pixel with a bit. This change creates a little error in the new picture. This Algorithm for one pixel to its neibouring acts mutually with considering expansion distribution error. If it be the first pixel amount and its new value be 255, the error value equals e = 255 – F. In Fluyd Steinberg’s method the error value in neibouring pixels is like what is shown in Figure 1, Will spread the value of error with different weights between neibouring pixels spreads that are at the right side or under pixel. For example if the right side pixel value mentioned be A, the new value will be A + 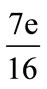 . In the method, we begin from the left corner and upper part of picture, and measure them as row and perform the error spread halftone.
. In the method, we begin from the left corner and upper part of picture, and measure them as row and perform the error spread halftone.
We divide the pictures into blocks with proper dimension, and then survey them to be simple or complicated [8]. If the total or most of pixels of a block are black or white, That block is simple. Figure 2 shows a simple 8 × 8 block.
Blocks which are not very monotonous are complicated blocks. Figure 3 shows an 8 × 8 complicated block.
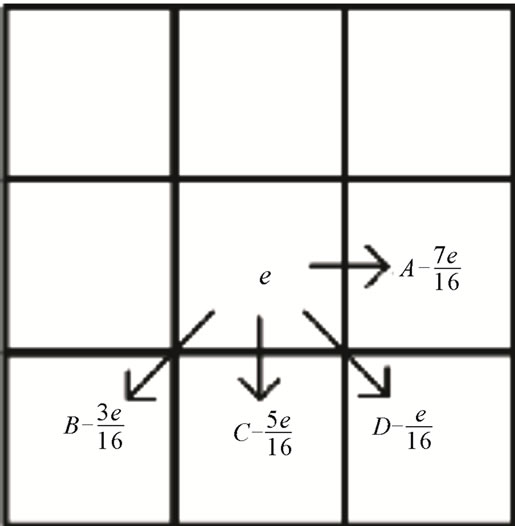
Figure 1. The error based on fluyd steinberg.

Figure 2. Simple block.

Figure 3. Complicated block.
The norm we have used for being complicated is the norm of complication between black and white that have explained in the reference. We divide the picture into block with proper dimensions of 16 × 16, then insert information in it. Suppose there is a border block between every two pixels. Generally, the number of border blocks are shown with measurement of N × M equals M(N – 1) + N(M – 1). M and N are the number of a picture blocks. These observations let us define a norm for complication based on the total of common borders between black and white pixels. Suppose T to pixel border is placed in a block and ∂ number of then are between black and white pixels. Then we can define the complication norm as a =
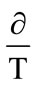 This norm exists in the extension of [0 - 1]. With the amount of threshold a0, we can differentiate the simple and complicated blocks. If a(B) ≥ a0, it is a complex B block and if not it is a simple B block the amount of a0 is usually chosen experimentally 0.3 [9]. The paper is organized as follow:
This norm exists in the extension of [0 - 1]. With the amount of threshold a0, we can differentiate the simple and complicated blocks. If a(B) ≥ a0, it is a complex B block and if not it is a simple B block the amount of a0 is usually chosen experimentally 0.3 [9]. The paper is organized as follow:
1) Proposed method;
2) Performance and security analysis of proposed method;
3) Simulation results;
4) Conclusion.
2. Proposed Method
Suppose q bit data is to place in a picture. The row of bits will be considered as the following set d = {d0, d1, d2,···, dn – 1} [10]. Simple method function in Figure 4 shows data embedded algorithm in pictures based on a block classification image.
First, we divide the image into blocks, we accommodate The block scheduling pseudo-random numbers with uniform distribution with a key value. Embedded in a uniform image areas make attack visual in uniform areas. To prevent these attacks should be do embedded in non-uniform regions. Then we examine the complexity of each block, if there is complexity Block, placing for halftone Otherwise the blocks are going to next. The Floyd Steinberg method to generate an error, this reduces image quality. You can optimize the above method. So instead we calculate the complexity in the block, we review of this complexity in the pixels. The compete placing trend for halftone with complex areas is shown in Figure 5.
Based on shown Algorithm in Figure 5 at first a PRNG is given value with a key. Then the picture is measured for left side and upper part, and the number of complex pixel of picture is obtained. In order to place the data monotonously in complex pixels, it is necessary to compute the number of complex pixels before begin the inserting. In this research a method has been represented

Figure 4. Simple method algorithm.
that complexity for every pixel is computed. A neibourhood is defined to compute the complexity of every pixel, and then the complexity of every pixel is computed in the neibourhood. After computing the number of complicated pixel on the grey surface all pixels on the grey surface are scrolled in this method. When there is complexity pixel, one complicated pixel is reduced, and a semirandom number is produced in the other case. For every pixel the semi-random no with monotonous distribution Rnd between 0 and 1 will be produced, and If it is less than , One bit will be placed or embedded. So if the considered bit dh equals zero, the new value of pixel p is zero, and if the new pixel value be one, the new pixel value will be 255. If we compare semi-random NO produced with
, One bit will be placed or embedded. So if the considered bit dh equals zero, the new value of pixel p is zero, and if the new pixel value be one, the new pixel value will be 255. If we compare semi-random NO produced with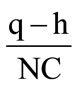 , in the end of placing exactly q bit data, and a monotonous will be inserted in picture surface. It is possible to miss the complexity of pixel because of inserting, and changes into a simple one, and it may disorder the process of taking out. For this reason, the pixel is tested after placing for complexity, and if it is still complex, one extra pixel is added to the index of data. If it has lost its complexity, the semi-random produced NO which is used to decide for inserting, it will be used for the next complex pixel in order to take out a row of random correctly. After getting new value pixel, the error taken place i.e. (p − pk) will be expanded that function Diffuse (p − pk) is carried out. It is natural that changing grey picture into halftone one creates some errors. Here, SNR1 is used as a norm to measure the created error. SNR norm is usual method to clarify error rate which explains the ratio of power potential of signal to noise. For a picture as large as M × N pixel, SNR is defined in Formula 1:
, in the end of placing exactly q bit data, and a monotonous will be inserted in picture surface. It is possible to miss the complexity of pixel because of inserting, and changes into a simple one, and it may disorder the process of taking out. For this reason, the pixel is tested after placing for complexity, and if it is still complex, one extra pixel is added to the index of data. If it has lost its complexity, the semi-random produced NO which is used to decide for inserting, it will be used for the next complex pixel in order to take out a row of random correctly. After getting new value pixel, the error taken place i.e. (p − pk) will be expanded that function Diffuse (p − pk) is carried out. It is natural that changing grey picture into halftone one creates some errors. Here, SNR1 is used as a norm to measure the created error. SNR norm is usual method to clarify error rate which explains the ratio of power potential of signal to noise. For a picture as large as M × N pixel, SNR is defined in Formula 1:

Figure 5. Behine method algorithm.
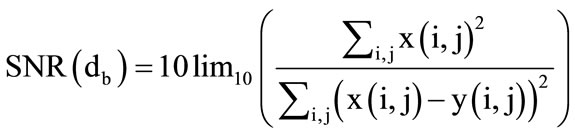 (1)
(1)
In it x(i, j) the value of pixel in line i and column j in real picture, and y(i, j) is the corresponding pixel value in changed picture. The important point is that because of inserting a block, it is possible for a block not to be complicated any more. This possibility creates problems for taking out the data. Because the procedure of exploiting is so that at first the picture is made as a block, and then examine if it is complex or not. If it was not a complex block, we go to the next one, if it was complex the data bits will be got out from semi-random place with the same key that has been used for placing. If the block was complex before inserting but the next one is not complex, when taking out we suppose NO data has been embedded. Of course this problem happens rarely. In this case, to solve this problem in placing process, after inserting every block, its complicated situation should be computed. If the block is not complicated any more, the placed data in it should be inserted or embedded in the next one again (h → hp). To exploit the inserted data in the stage medium picture when have the key and length of inserted data PRNG2 used for the first value, At first based on the above method we should compute the number of complex pixels [11]. Then from the left corner and the upper part of the picture begin to calculate the complexity of every pixel and if so a semi random number is produced and we recognize the PRNG pixels containing data. Figure 6 shows the Algorithm extract.
3. Performance and Security Analysis of Proposed Method
Photos are sensitive to visual attacks it means the visual system of human is able to recognize the existence of data in the picture [12]. Data placement in photos in white areas causes the picture be attacked by vision. So then in this case it maybe possible that human be able to recognize
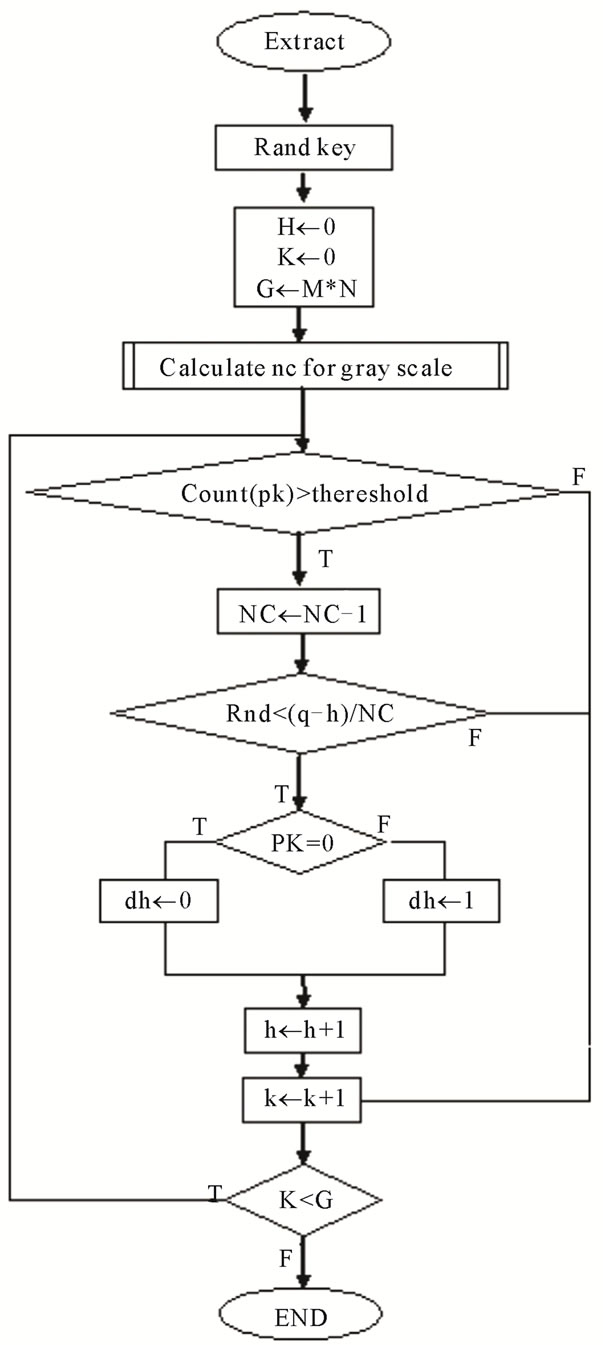
Figure 6. Extract algorithm.
the hidden data in the picture. Placement in white area creates some black points that it shows placement of zero bits message has been performed in that areas, it is the major fault of data placement in the picture [13]. Now inorder to prevent these attacks we should divide the photo in blocks as M × N. Then place information in the blocks which are not monotonous. Blocks which are not monotonous are all called complicated ones. So we should compute the complexity for every block and then place the information. To do this, we begin the review from the left side of the first block. Performing the suggested method improves the quality of placing picture and increases its security.
4. Simulation Results
The placement is carried out after making halftone in the presented methods in refrences [4-6]. Placement of data in photos after creating halftone causes some noise be performed around the area of filter which has a medium grey color. In the suggested method, placement of information in the picture takes place simultanously with creating halftone so that created error because of placement of information like halftone of performing error is distributed in neibouring pixels. Placement in the process of making halftone in relation to placement in halftone increase the quality of picture that inturn causes the increase of security or capacity. In this method, the embedded data in image Halftone such that the error resulting from the spread to adjacent pixels. The proposed method of error resulting from data embedded in the adjacent pixels Maintain image quality and higher capacity utilization has been. This method of uniform or nonuniform criteria for the pixels in images which has significantly reduced errors and improved quality. The proposed method has been implemented by matlab software The implementation for the second image has been reviewed and the results in Table 1 are shown.
Figure 7 has been shown Main Picture, Figure 8 has been shown after making Halftone action will not be
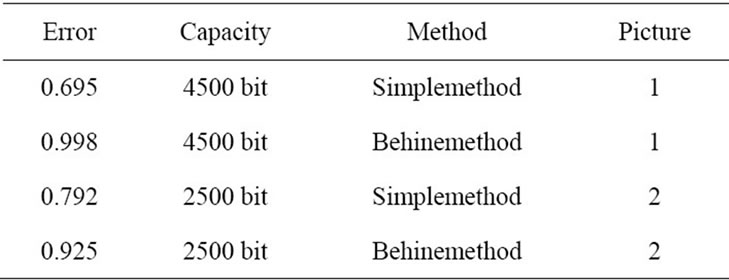
Table 1. Show the simulation result.

Figure 7. Main picture.
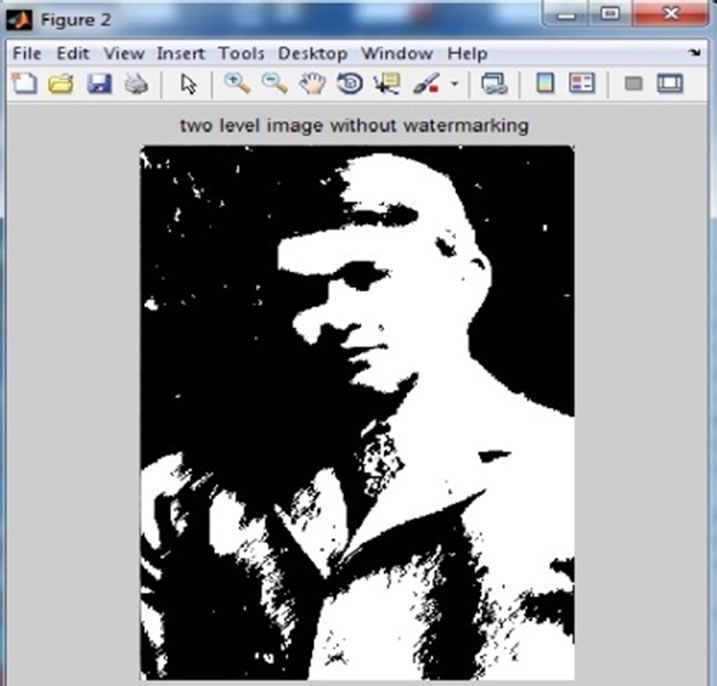
Figure 8. Halftone picture.
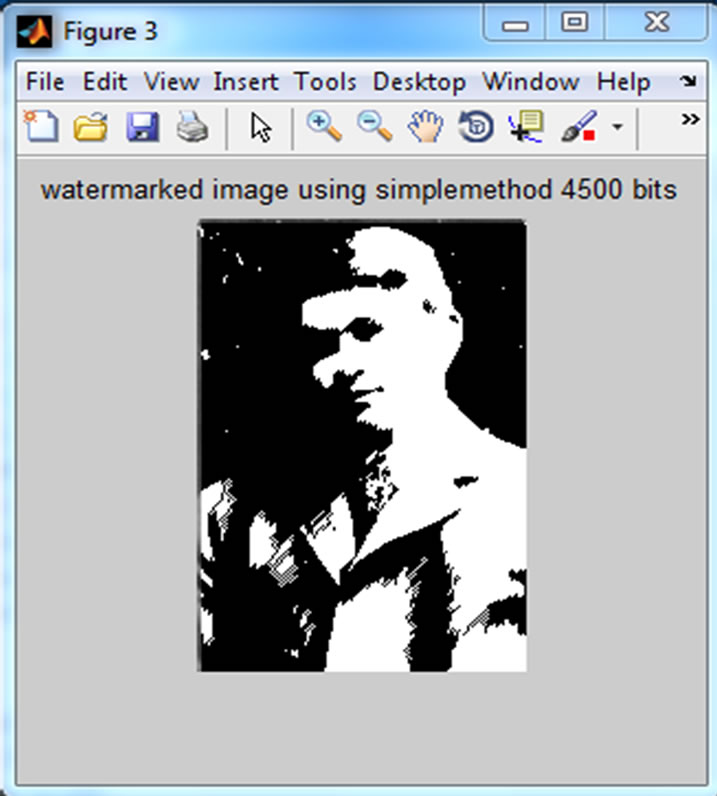
Figure 9. Simple method.
embedded and Figure 9 has been shown placing with Simple method and Figure 10 has been shown placing with Behine method.
5. Conclusion
A method for steganography was presented. The action of inserting and halftone is performed at the same time, and the resulted error from placing diffused to neibouring pixels, placing in simple picture can discover steganography by eyes. A norm was used to distinguish sim-
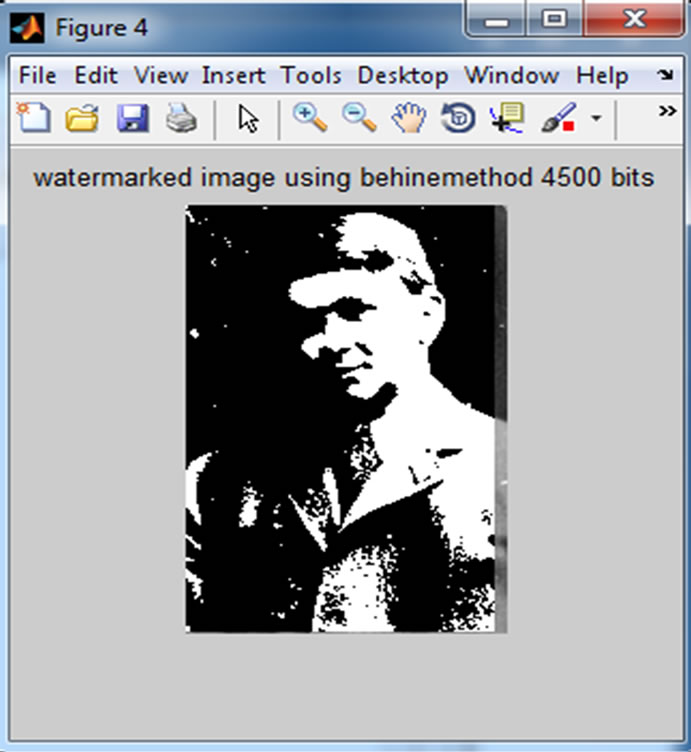
Figure 10. Behine method.
ple blocks, and suggested a method to prevent inserting in simple picture blocks. In some steganographies the step of inserting comes after making halftone that reduces the capacity a lot. In the suggested method the diffusion of error resulted by inserting in the neibouring pixels improves the picture quality and usage compared with former methods. The suggested method has used the norm of complexity that reduces error clearly and improves quality. Disassembling operations show the precision and correctness of the method.
REFERENCES
- C.-S. Shieh, H.-C. Huang, F.-H. Wang and J.-S. Pan, “Genetic Watermarking Based on Transform-Domain Techniques,” Pattern Recognition, Vol. 37, No. 3, 2004, pp. 555-565. doi:10.1016/j.patcog.2003.07.003
- P. Wayner, “Disappearing Cryptography: Information Hiding: Steganography and Watermarking,” 2nd Edition, Morgan Kaufmann Publishers Inc., San Francisco, 2002.
- M. Y. Wu and J. H. Lee, “A Novel Data Embedding Method for Two-Color Facsimile Images,” Proceeding of International Symposium on Multimedia Information Processing (ICASSP), Vol. 2, 1998, pp. 1161-1164.
- Y. C. Tseng, Y. Y. Chen and H.-K. Pan, “A Secure Data Hidding Scheme for Binary Images,” IEEE Transaction on Communications, Vol. 50, No. 8, 2002, pp. 1227-1231. doi:10.1109/TCOMM.2002.801488
- T. Mitsa and K. Parker, “Digital Halftoning Using a Blue Noise Mask,” Journal of Optical Society of America A, Vol. 9, No. 11, 1992, pp. 1920-1929. doi:10.1364/JOSAA.9.001920
- M. Wu, E. Tang and B. Liu, “Data Hiding in Digital Binary Image,” Proceeding of IEEE International Conference on Multimedia & Expo, New York, 2000, pp. 393- 396.
- R. W. Floyd and L. Steinberg, “Adaptive Algorithm for Spatial Grayscale,” Proceedings of SID, Vol. 17, No. 2, 1976, pp. 75-77.
- T. N. Pappas, J. P. Allebach and D. L. Neuhoff, “ModelBased Digital Halftoning,” IEEE Signal Processing Magazine, Vol. 20, No. 4, 2003, pp. 14-27. doi:10.1109/MSP.2003.1215228
- E. Kawaguchi and R. O. Eason, “Principle and Applications of BPCS Steganography,” Proceedings of SPIE’s International Symposium on Voice, Video, and Data Communications, 1998, pp. 464-473.
- M. S. Fu and O. C. Au, “Data Hiding Watermarking for Halftone Images,” IEEE Transactions on Image Processing, Vol. 11, No. 4, 2008, pp. 477-484.
- M. Jiang, E. K. Wong, N. Memon and X. Wu, “Steganalysis of Halftone Images,” Proceedings of ICASSP, Vol. 2, 2009, pp. ii/793-ii/796.
- S. H. Kim and J. P. Allebach, “Impact of Human Visual System Models on Model Based Halftoning,” IEEE Transaction on Image Processing, Vol. 11, 2004, pp. 258- 269.
- H. K. Verma and A. N. Singh, “Robustness of the Digital Image Watermarking Techniques against Brightness and Rotation Attack,” International Journal of Computer Science and Information Security, Vol. 5, No. 1, 2010.
NOTES
1Signal to Noise Ratio.
2Pesudo Random Number Generator.

