Materials Sciences and Applications
Vol.06 No.08(2015), Article ID:58661,9 pages
10.4236/msa.2015.68076
Nonlinear Bending of Piezoelectric Cylindrical Shell Reinforced with BNNTs under Electro-Thermo-Mechanical Loadings
Jinhua Yang*, Pengjun Zhang
School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha, China
Email: *yangjinhua01@tom.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 July 2015; accepted 2 August 2015; published 7 August 2015
ABSTRACT
Under combined electro-thermo-mechanical loadings, the nonlinear bending of piezoelectric cylindrical shell reinforced with boron nitride nanotubes (BNNTs) is investigated in this paper. By employing nonlinear strains based on Donnell shell theory and utilizing piezoelectric theory including thermal effects, the constitutive relations of the piezoelectric shell reinforced with BNNTs are established. Then the governing equations of the structure are derived through variational principle and resolved by applying the finite difference method. In numerical examples, the effects of geometric nonlinear, voltage, temperature, as well as volume fraction on the deflection and bending moment of axisymmetrical piezoelectric cylindrical shell reinforced with BNNTs are discussed in detail.
Keywords:
Nonlinear Bending, Piezoelectric, Cylindrical Shell, BNNT, Electro-Thermo-Mechanical Loadings

1. Introduction
BNNTs are similar to CNTs in structure and their extraordinary mechanical properties, but are different in that BNNTs possess higher temperature resistance to oxidation and stronger piezoelectric characteristics. Also, unlike CNTs, BNNTs have stable semiconducting behavior with a large band gaps regardless of radius and chirality of the structure. This property of BNNTs makes them promising candidate materials in a large variety of nanosized electronic and photonic devices. Therefore, BNNTs seem to be more suitable as reinforcement in composite structures due to their high resistance to oxidation at elevated temperatures [1] , outstanding mechanical properties [2] and high thermal conductivity [3] . With the development of science and technology, a new sort of smart nanocomposites, with piezoelectric material as matrix and BNNTs as the reinforcement, has attracted increasing interests in both research and engineering communities. It is noted that the investigations on this new smart nanocomposites are limited in number and most discuss the linear problem. Therefore, it is necessary to do more extensive researches on the nonlinear behavior for this structure.
At present, most researches are limited to discussing the behavior of piezoelectric structure without reinforce- ment of BNNTs. Yao et al. [4] presented static behaviors of piezoelectric cantilever actuator under large electric field. Shen [5] studied the nonlinear bending for a simply supported, shear deformable cross-ply laminated plate with piezoelectric actuators subjected to a transverse uniform or sinusoidal load combined with electrical loads and in thermal environments. Shegokar et al. [6] deals with the stochastic nonlinear bending response of functionally graded materials beam with surface bonded piezoelectric layers subjected to thermo-electro-mechanical loadings. Narita et al. [7] illustrated an analytical and experimental study of nonlinear bending response and domain wall motion in piezoelectric laminated actuators under electric fields. Beldica et al. [8] analyzed the bending of nonlinear viscoelastic beams with small or large deformations. Yan et al. [9] investigated the time- dependent behavior of a simply supported, angle-ply piezoelectric laminate in cylindrical bending with viscoelastic interfaces. Narita et al. [10] discussed the static electromechanical displacement and polarization switching properties of piezoelectric laminated actuators under three point bending. Using a variational formulation, Li et al. [11] developed a size-dependent functionally graded piezoelectric beam model. Based on the local Petrov- Galerkin approach, Sladek et al. [12] proposed a meshless method for plate bending analysis with functionally graded piezoelectric material properties. Employing Euler-Bernoulli beam theory and the physical neutral surface concept, Fu et al. [13] presented the thermo-piezoelectric buckling, nonlinear free vibration and dynamic stability for the piezoelectric functionally graded beams. None of the above mentioned works have considered the behavior of piezoelectric structure reinforced with BNNTs.
Recently, some researches about the static buckling of piezoelectric shell reinforced with BNNTs have emerged. Buckling of BNNTs in a PVDF elastic medium subjected to combined electro-thermo-mechanical loadings was investigated by Salehi-Khojin and Jalili [14] who showed that applying direct and reverse voltages to BNNT changed buckling loads for any axial and circumferential wave-numbers. Mosallaie Barzoki et al. [15] studied torsional linear buckling of a PVDF cylindrical shell reinforced by BNNTs with an elastic core under the same loading condition as [14] were investigated, indicating that buckling strength increased substantially as harder foam cores were employed. Using virtual displacement method based on nonlocal cylindrical piezoelasticity continuum shell theory, Arani et al. [16] discussed the axial buckling of double-walled Boron Nitride nanotubes embedded in an elastic medium under combined electro-thermo-mechanical loadings. Up to now, to the best of authors’ knowledge, the research on nonlinear bending of piezoelectric shell reinforced with BNNTs has not been reported in the open literature.
Motivated by the considerations, we aim to study the nonlinear bending of axisymmetrical piezoelectric shell reinforced with BNNTs under combined electro-thermo-mechanical loadings. Using the difference method in space, the whole problem is resolved by the iteration method. Numerical results in nonlinear deflection and bending moment of axisymmetrical piezoelectric cylindrical shell reinforced with BNNTs are presented for different values of voltage, temperature, volume fraction and so on.
2. Basic Equations
Consider that a piezoelectric cylindrical shell reinforced with BNNTs has midsurface radius R, thickness h, length L and mass density 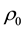 (see Figure 1). The shell is referred to the coordinate system (x, y, z) in which x and y are the axial and circumferential directions of the shell and z is in the direction of the inward normal to the middle surface. The origin of the coordinate system is located at the end of the shell on the middle plane. The shell is subjected to transverse static load
(see Figure 1). The shell is referred to the coordinate system (x, y, z) in which x and y are the axial and circumferential directions of the shell and z is in the direction of the inward normal to the middle surface. The origin of the coordinate system is located at the end of the shell on the middle plane. The shell is subjected to transverse static load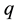 , applied voltage V and a uniform temperature rise
, applied voltage V and a uniform temperature rise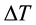 .
.
2.1. Strain Displacement Relationships
Supposing that 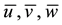 denote the axial, circumferential and radial displacement of an arbitrary point on the shell, and the corresponding displacement components of middle surface are
denote the axial, circumferential and radial displacement of an arbitrary point on the shell, and the corresponding displacement components of middle surface are 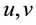 and
and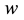 , then the displacement components of piezoelectric cylindrical shell can be written as
, then the displacement components of piezoelectric cylindrical shell can be written as
Figure 1. (a) Geometry of piezoelectric cylindrical shell reinforced with BNNTs; (b) section of cylindrical shell.
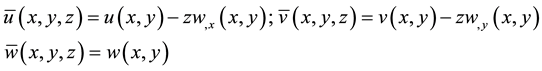 (1)
(1)
where the inferior mark (,) denotes the partial derivative to variables coordinate.
Based on classical shell theory with von Kármán-Donnell type kinematic relations, the nonlinear strain-dis- placement relations can be expressed as
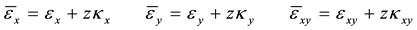 (2)
(2)
where 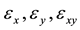 are the strain components on the middle surface and
are the strain components on the middle surface and 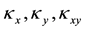 are the change values of curvatures on the middle surface, and
are the change values of curvatures on the middle surface, and
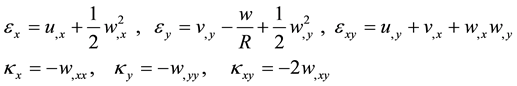 (3)
(3)
2.2. Constitutive Equations
The constitutive relationship of a piezoelectric structure under combined mechanical, thermal and electrical loadings can be expressed as follows [15]
 (4)
(4)
 (5)
(5)
where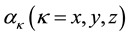 ,
, 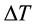 and
and 


where

Superscripts r and m refer to the reinforced and matrix components of the composite, respectively. 
2.3. Governing Equations
For the piezoelectric cylindrical shell reinforced with BNNTs, the total potential energy 

where 

The expression of the strain energy is

Considering Equations (4) and (5), as well as the zigzag structure for BNNTs employed here, and the longitudinal arrangement of strips in matrix, makes

Letting V is the voltage applied on both ends of shell, then

The work done by the transverse load 

Applying the variational principle

where

in which

In the above equations, the 

Under the axisymmetrical circumstances, the circumferential displacement 



the nonlinear governing equations of axisymmetrical piezoelectric shell reinforced with BNNTs under electro- thermo-mechanical loadings can be reduced as

where,
Supposing the both ends of the shell are clamped, then the dimensionless boundary conditions are respectively as follows:

where

3. Solution Methodology
For seeking the solution of differential Equation (18) with boundary condition (19), the dimensionless displacement functions 

Difference method is adopted in space domain. For the disposal of linear item, taking 

Referring to difference scheme, the difference expressions of the other linear items in governing equation can be easily achieved.
Then the nonlinear items of governing equations are linearized and can be written as follows [18] ,

in which 


As for different iterations, the coefficients



After the equations and conditions are linearized and disposed by using the finite difference method, the nonlinear partial differential equations are transformed into linear algebraical equations expressed by difference schemes. These algebraic equations are solved by using the iteration method. For every step, the iterative lasts until the difference of the present value and the former is smaller than 0.01%, then continues the calculation of the next step.
4. Numerical Results and Discussion
The nonlinear bending of piezoelectric shell reinforced with BNNTs under electro-thermo-mechanical loadings is investigated in the following calculations. The geometrical parameter of the shell is


The effects of geometric nonlinear on the bending of piezoelectric shell reinforced with BNNTs are presented in Figure 2(a) and Figure 2(b). The volume fraction


From the two figures, it can be noticed that the dimensionless deflection and bending moment of the shell in linear case is greater than that in nonlinear case, and this phenomenon becomes more evident when the transverse load Q increases. As we know, the linearity case is based on the limited deformation consumption, and the higher order item in the geometric relations is neglected while it is in consideration for the nonlinear case. So in some sense it can be concluded that the linear lowly predicts the stiffness of the structure. In order to reflect the property of the piezoelectric shell reinforced with BNNTs accurately, the consideration of the nonlinear effect is very necessary.
Figure 3 shows the effect of positive and negative voltage on the nonlinear bending of piezoelectric shell reinforced with BNNTs. The volume fraction


The effects of temperature on the nonlinear bending of the shell are presented in Figure 4. The volume fraction


The effect of volume fraction on the nonlinear bending of piezoelectric shell reinforced with BNNTs is discussed in Figure 5. The voltage is

Table 1. Mechanical, electrical and thermal properties of PVDF and BNNT.

Figure 2. Effect of geometric nonlinear on bending of piezoelectric shell reinforced with BNNTs; (a) Deflection of each point along x; (b) Bending moment of each point along x.

Figure 3. Effect of voltage on nonlinear bending of piezoelectric shell reinforced with BNNTs; (a) Deflection of each point along x; (b) Bending moment of each point along x.

Figure 4. Effect of temperature on nonlinear bending of piezoelectric shell reinforced with BNNT; (a) Deflection of each point along x; (b) Bending moment of each point along x.

Figure 5. Effect of volume fraction on nonlinear bending of piezoelectric shell reinforced with BNNT. (a) Deflection of each point along x; (b) Bending moment of each point along x.
in this figure. It can be noticed that the deflection and the bending moment decrease when the volume fraction of BNNT in matrix 
5. Conclusions
In present study, the governing equations of nonlinear bending are presented for piezoelectric cylindrical shell reinforced with BNNTs under combined electro-thermo-mechanical loadings. Results indicate that some parameters, including geometric nonlinear, voltage, temperature, volume fraction and so on, have significant influence on the deflection and bending moment of the shell. The following conclusions may be drawn from the present work:
1) The deflection and bending moment of the shell in linear case is greater than that in nonlinear case, and the nonlinear effect enhances when the transverse load 
2) Applying positive and negative voltage to BNNT leads to increase and decrease of the deflection and bending moment.
3) The deflection as well as the bending moment increases with the increase of temperature, and decreases when the volume fraction of BNNT in matrix increases.
Acknowledgements
The work described in this paper was supported by National Natural Science Foundation of China (No: 11102028, 11202038, 11172051) and Research Foundation of Education Bureau of Hunan Province, China (No: 11B005).
Cite this paper
JinhuaYang,PengjunZhang, (2015) Nonlinear Bending of Piezoelectric Cylindrical Shell Reinforced with BNNTs under Electro-Thermo-Mechanical Loadings. Materials Sciences and Applications,06,743-752. doi: 10.4236/msa.2015.68076
References
- 1. Chen, Y., Zou, J., Campbell, S.J. and Le Caer, G. (2004) Boron Nitride Nanotubes: Pronounced Resistance to Oxidation. Applied Physics Letters, 84, 2430-2432.
http://dx.doi.org/10.1063/1.1667278 - 2. Suryavanshi, A.P., Yu, M.F., Wen, J.G., Tang, C.C. and Bando, Y. (2004) Elastic Modulus and Resonance Behavior of Boron Nitride Nanotubes. Applied Physics Letters, 84, 2527-2529.
http://dx.doi.org/10.1063/1.1691189 - 3. Terrones, M., Romo-Herrera, J.M., Cruz-Silva, E., López-Urías, F., Muñoz-Sandoval, E., Velázquez-Salazar, J.J., Terrones, H., Bando, Y. and Golberg, D. (2007) Pure and Doped Boron Nitride Nanotubes. Materials Today, 10, 30-38.
http://dx.doi.org/10.1016/S1369-7021(07)70077-9 - 4. Yao, L.Q., Zhang, J.G., Lu, L. and Lai, M.O. (2004) Nonlinear Static Characteristics of Piezoelectric Bending Actuators under Strong Applied Electric Field. Sensors and Actuators A: Physical, 115, 168-175.
http://dx.doi.org/10.1016/j.sna.2004.04.037 - 5. Shen, H.-S. (2004) Nonlinear Bending Analysis of Unsymmetric Cross-Ply Laminated Plates with Piezoelectric Actuators in Thermal Environments. Composite Structures, 63, 167-177.
http://dx.doi.org/10.1016/S0263-8223(03)00145-4 - 6. Shegokar, N.L. and Lal, A. (2013) Stochastic Nonlinear Bending Response of Piezoelectric Functionally Graded Beam Subjected to Thermoelectromechanical Loadings with Random Material Properties. Composite Structures, 100, 17-33.
http://dx.doi.org/10.1016/j.compstruct.2012.12.032 - 7. Narita, F., Shindo, Y. and Mikami, M. (2005) Analytical and Experimental Study of Nonlinear Bending Response and Domain Wall Motion in Piezoelectric Laminated Actuators under Electric Fields. Acta Materialia, 53, 4523-4529.
http://dx.doi.org/10.1016/j.actamat.2005.05.044 - 8. Beldica, C.E. and Hilton, H.H. (2001) Nonlinear Viscoelastic Beam Bending with Piezoelectric Control-Analytical and Computational Simulations. Composite Structures, 51, 195-203.
http://dx.doi.org/10.1016/S0263-8223(00)00139-2 - 9. Yan, W., Wang, J. and Chen, W.Q. (2014) Cylindrical Bending Responses of Angle-Ply Piezoelectric Laminates with Viscoelastic Interfaces. Applied Mathematical Modelling, 38, 6018-6030.
http://dx.doi.org/10.1016/j.apm.2014.05.025 - 10. Narita, F., Shindo, Y. and Hayashi, K. (2005) Bending and Polarization Switching of Piezoelectric Laminated Actuators under Electromechanical Loading. Computers & Structures, 83, 1164-1170.
http://dx.doi.org/10.1016/j.compstruc.2004.08.025 - 11. Li, Y.S., Feng, W.J. and Cai, Z.Y. (2014) Bending and Free Vibration of Functionally Graded Piezoelectric Beam Based on Modified Strain Gradient Theory. Composite Structures, 115, 41-50.
http://dx.doi.org/10.1016/j.compstruct.2014.04.005 - 12. Sladek, J., Sladek, V., Stanak, P., Zhang, C.Z. and Wünsche, M. (2013) Analysis of the Bending of Circular Piezoelectric Plates with Functionally Graded Material Properties by a MLPG Method. Engineering Structures, 47, 81-89.
http://dx.doi.org/10.1016/j.engstruct.2012.02.034 - 13. Fu, Y.M., Wang, J.Z. and Mao, Y.Q. (2012) Nonlinear Analysis of Buckling, Free Vibration and Dynamic Stability for the Piezoelectric Functionally Graded Beams in Thermal Environment. Applied Mathematical Modelling, 36, 4324-4340.
http://dx.doi.org/10.1016/j.apm.2011.11.059 - 14. Salehi-Khojin, A. and Jalili, N. (2008) Buckling of Boron Nitride Nanotube Reinforced Piezoelectric Polymeric Composites Subject to Combined Electro-Thermo-Mechanical Loadings. Composites Science and Technology, 68, 1489-1501.
http://dx.doi.org/10.1016/j.compscitech.2007.10.024 - 15. Mosallaie Barzoki, A.A., Arani, A.G., Kolahchi, R. and Mozdianfard, M.R. (2012) Electro-Thermo-Mechanical Torsional Buckling of a Piezoelectric Polymeric Cylindrical Shell Reinforced by DWBNNTs with an Elastic Core. Applied Mathematical Modelling, 36, 2983-2995.
http://dx.doi.org/10.1016/j.apm.2011.09.093 - 16. Arani, A.G., Amir, S., Shajari, A.R. and Mozdianfard, M.R. (2012) Electro-Thermo-Mechanical Buckling of DWBNNTs Embedded in Bundle of CNTs Using Nonlocal Piezoelasticity Cylindrical Shell Theory. Composites Part B: Engineering, 43, 195-203.
http://dx.doi.org/10.1016/j.compositesb.2011.10.012 - 17. Tan, P. and Tong, L.Y. (2001) Micro-Electromechanics Models for Piezoelectric-Fiber-Reinforced Composite Materials. Composites Science and Technology, 61, 759-769.
http://dx.doi.org/10.1016/S0266-3538(01)00014-8 - 18. Fu, Y.M. (1997) Nonlinear Dynamic Analysis of Structures. Jinan University Press, Guangzhou.
NOTES
*Corresponding author.






