Materials Sciences and Applications
Vol.3 No.11(2012), Article ID:24728,11 pages DOI:10.4236/msa.2012.311112
Physical Properties of the ZnxCd1–xSe Alloys: Ab-Initio Method
![]()
1Department of Physics, University Djillali Liabes, Sidi Bel Abbes, Algeria; 2Laboratoire Microscopy, Microanalysis of Matter and Molecular Spectroscopy, University Djillali Liabes, Sidi Bel Abbes, Algeria; 3Laboratory of Communication Networks, Architecture and Multimedia, Sidi-Bel-Abbès University, Sidi Bel Abbès, Algeria.
Email: *lttnsameri@yahoo.fr
Received August 3rd, 2012; revised September 2nd, 2012; accepted October 1st, 2012
Keywords: FP-LMTO; Ab-Initio; Approach of Zunger; Effective Mass
ABSTRACT
The present work performs self-consistent ab initio full-potential linear muffin-tin orbital (FP-LMTO) method to study the structural and electronic properties of the ternary ZnxCd1−xSe alloy, based on density functional theory (DFT). In this approach, both the local density approximation (LDA) and the generalized gradient approximation (GGA) were used for the exchange-correlation potential calculation. The ground-state properties are determined for the bulk materials CdSe, ZnSe and their alloy in cubic phase. In particular, the lattice constant, bulk modulus, electronic band structures and effective mass. We mainly showed deviation of the lattice parameter and bulk modulus from Vegard’s law of our alloys. We also presented the microscopic origins of the gap bowing using the approach of Zunger et al. The results are compared with other theoretical calculations and experimental data and are in reasonable agreement.
1. Introduction
In recent years II-VI semiconductors have received much attention because of their technological potential applications, ranging from optoelectronic devices such as light emitting diodes [1,2], solar cells [3,4], displays [5,6], photovoltaic cells [7,8] to luminescence biological tags [9,10]. Their mixed II-VI ternary semiconductors are used in optoelectronic devices ranging from blue to nearultraviolet spectral region [9-11]. These materials are also used for manufacturing X-ray, γ-ray detectors [12, 13]. Cd based compounds can also be used as an alternative material for short and medium wavelength infrared focal plane arrays [13,14]. Among them, ZnSe and CdSe which are members of the II-VI semiconductors are technologically important materials due to their direct and rather large gap. ZnSe compounds have cubic (zinc blende) structure [15,16], whereas CdSe compounds depending on the growth condition may have both zinc blende and wurtzite (hexagonal) structures at normal conditions. Theoretical studies indicate that CdSe compounds are stable in both zinc blende and wurtzite structures [17-19], we choose the zinc-blende phase, since it has fewer atoms in unit cell, and is therefore computationally easier to treat. The structural and electronic properties of these compounds have been investigated, both experimentally and theoretically during the past 50 years. ZnxCd1−xSe mixed crystals have recently been studied theoretically [20,21] and experimentally [22,23]. With different methods for example, Suzuki and Adachi [24] have calculated the optical constants of ZnxCd1−xSe (for x = 0, 0.47, 0.53, 1) using the first-principle methods. Electronic and optical properties of ZnxCd1−xSe (for x = 0, 0.25, 0.75, 1) have been investigated using the empirical pseudopotential method (EPM) by Benosman et al. [21]. Kim et al. [22] have investigated optical properties of ZnxCd1−xSe films grown on GaAs. Samarth et al. [23] have studied the composition (x) dependence of the fundamental gap of ZnxCd1−xSe based on the reflection spectroscopy.
In this work, we have aimed to provide some additional information to the existing data on disorder effect of ZnxCd1−xSe mixed crystals using the FP-LMTO method [25,26] to have an idea about their behaviors. The physical origins of gap bowing are calculated following the approach of Zunger and co-workers, all first we compare and investigate the structural, and electronic properties of ZnSe and CdSe compound using LDA, GGA.
The paper is organized as follows: Section 2 describes briefly the method used, in Section 3 we present our results concerning structural, electronic, bowing parameters, effective masses and we make a comparison with values reported in the literature, a final Section 4 presents our conclusions.
2. Method of Calculations
In order to calculate the structural and electronic properties of ZnxCd1−xSe alloys, we have employed the FPLMTO method to solve the Kohn Sham equations. We have performed our calculations by Lmtart code [27] within the framework of density functional theory (DFT) [28] that has been shown to yield reliable results for the electronic and structural properties of various solids. For the exchange-correlation potential we have used both the local density approximation (LDA) [29] and the generalized gradient approximation (GGA) based on Perdew et al. [30]. The FP-LMTO method treats muffin-tin spheres (MTS) and interstitial regions (IR) on the same footing, leading to improvements in the precision of the eigenvalues. At the same time, the FP-LMTO method, in which the space is divided into (IR) and non overlapping (MTS) surrounding the atomic sites, uses a more complete basis than its predecessors. In the IR regions, the basis functions are represented by Fourier series. Inside the MTS, the basis functions are represented in terms of numerical solutions of the radial Schrödinger equation for the spherical part of the potential multiplied by spherical harmonics. The charge density and the potential are represented inside the MTS by spherical harmonics up to lmax = 6. There is a parameter must be defined whenever a DFT calculation is performed the cut-off energy Ecut. In many ways, this parameter is easier to define than k points. The integrals over the Brillouin zone are performed up to 22 special k-points for binary compounds, 24 special k-points for the x = 0.25, x = 0.75 and 46 special k-points x = 0.5 of ZnxCd1−xSe alloys in the irreducible Brillouin zone (IBZ), using the Blöchl’s modified tetrahedron method [31]. The self-consistent calculations are considered to be converged when the total energy of the system is stable within 10–5 Ry. In order to avoid the overlap of atomic spheres the MTS radius for each atomic position is taken to be different for each case. Both the plane waves’ cut-off is varied to ensure the total energy convergence. The values of the sphere radii MTS, number of plane waves (NPLW), and cut-off energy Ecut used in our calculation are summarized in Table 1.
3. Results and Discussion
3.1. Structural Properties
At first, a set of total energy calculation versus unit cell volume E (V), for binary compounds CdSe, ZnSe structure and their ternary alloys in zinc-blende were carried out in order to determine the structural parameters. We model the alloys at some selected compositions x = 0.25, 0.5 and 0.75, with ordered structures described in terms of periodically repeated supercells containing eight atoms. The corresponding values are fitted with the Murnaghan equation of state [32]. The equilibrium structural properties such as the lattice constants a0 and bulk modulus B0 were obtained for both binary compounds and their alloys, the results are given in Table 2. Considering the general trend that GGA usually overestimates the lattice parameters [33] on the other side are underestimated through local density approximation (LDA). The results obtained in this work are in close agreement with those obtained experimentally and are better than results
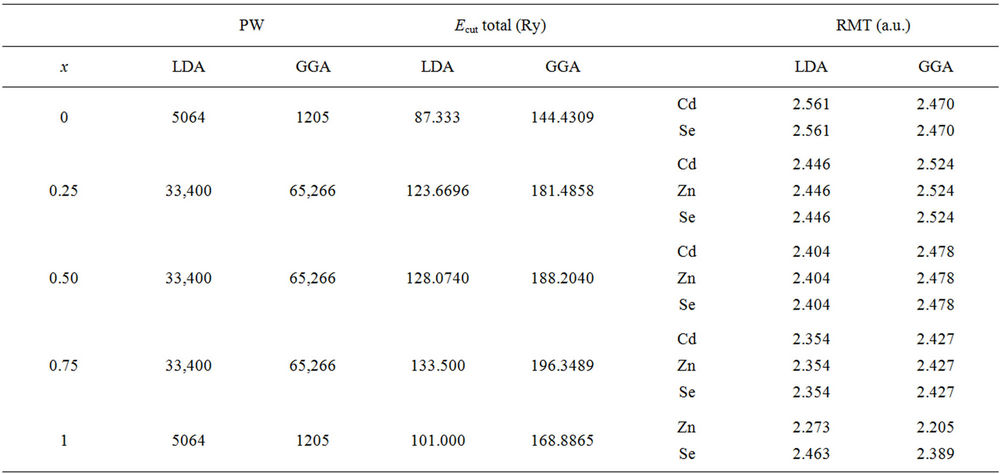
Table 1. The plane wave number PW, energy cut-off (in Ry) and muffin-tin radius (RMT) (in a.u.) used in calculation for binary CdSe, ZnSe and their alloys in Zinc-blende structure.
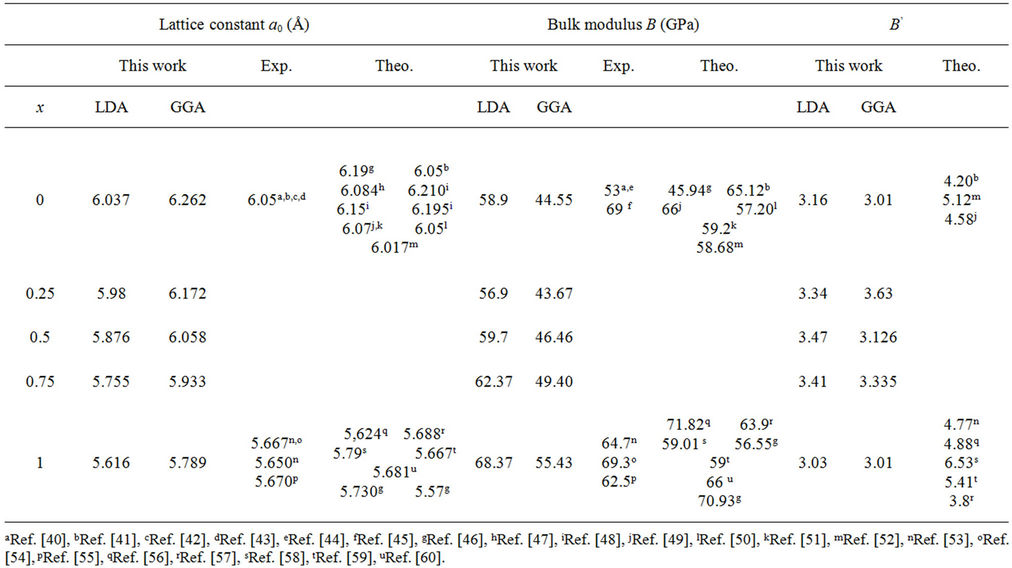
Table 2. Calculated lattice parameter (a0), bulk modulus (B) and its pressure derivative (B’) compared to experimental and theoretical values of CdSe, ZnSe and ZnxCd1−x Se alloy.
obtained using other methods. It can be seen that the lattice constant of ZnxCd1−xSe alloy linear decreases as the composition x increases. Also, the order of compressibility from high to low is: CdSe > Cd 0.75Zn0.25 SeCd 0.5Zn0.5 Se Cd 0.25Zn0.75 Se ZnSe. This diminution may stem from the lower mass of Zn atom than that of the Cd atom. For these configurations, the largest value of bulk modulus (68.37 GPa; 55, 43 GPa) with LDA and GGA respectively, was obtained for ZnSe, therefore it has the higher compressibility and it may be a more compressible compound. Usually, in the treatment of alloys, it is assumed that the atoms are located at the ideal lattice sites and the lattice constant varies linearly with the composition x according to the so-called Vegard’s law [34]:
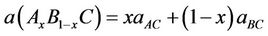 (1)
(1)
where aAC and aBC are the equilibrium lattice constants of the binary compounds AC and BC, respectively, and a (AxB1−x C) is the alloy lattice constant. However, deviation from Vegard’s law has been observed in semiconductor alloys both experimentally [35] and theoretically [36,65]. Hence, the lattice constant can be written as:
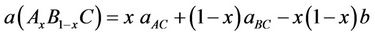 (2)
(2)
where the quadratic term (b) is the bowing parameter.
Figures 1 and 2, shows the calculated lattice constants and bulk modulus for each x of ZnxCd1−xSe along with Vegard’s law (v.z. the lattice constant of alloys should vary linearly with composition x [35]). Our calculated lattice parameters at different compositions of ZnxCd1−xSe alloy were found to vary almost linearly with a marginal upward bowing parameter. Using the LDA approximation equals to –0.206 Å and 15.21 GPa for the lattice constant and bulk modulus, respectively. While, the GGA approximation gave values of –0.139 Å and 15.96 GPa for the bowing lattice parameter and the bulk modulus, respectively, Hence the Vegard’s law is valid for this alloy. The physical origin of this marginal bowing parameter should be mainly due to the weak mismatches of the lattice constants of ZnSe and CdSe compounds.
3.2. Electronic Properties
To investigate the electronic properties of ZnSe and CdSe compounds as well as their alloy, we have calculated the band structure the high symmetry directions in the first Brillouin zone in the cubic phase structures within LDA and GGA using calculated equilibrium lattice constants as obtained previously. The valence band maximum (VBM) and the conduction band minimum (CBM) occur at the 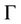 point; hence these compounds are semiconductors with direct energy band gaps
point; hence these compounds are semiconductors with direct energy band gaps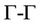 . This direct energy band gap increased from CdSe (x = 0) to Zn (x = 1). The results of this calculation are compared with experimental values and results from other works in Table 3, the band gaps are smaller than the experimental
. This direct energy band gap increased from CdSe (x = 0) to Zn (x = 1). The results of this calculation are compared with experimental values and results from other works in Table 3, the band gaps are smaller than the experimental
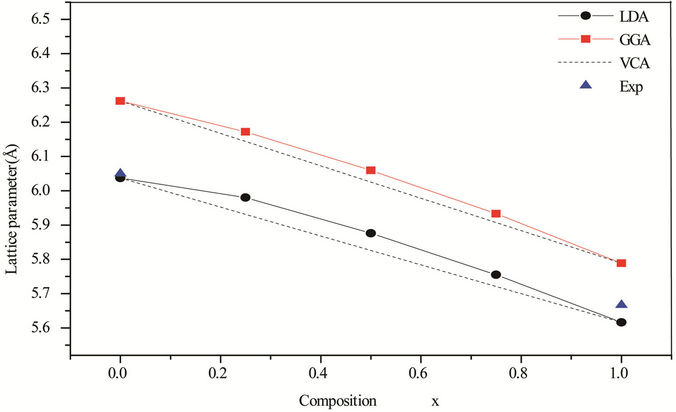
Figure 1. Composition dependence of the calculated lattice constants within LDA (solid circle) and GGA (solid square) of ZnxCd1−xSe alloy compared with experimental (solid triangle).
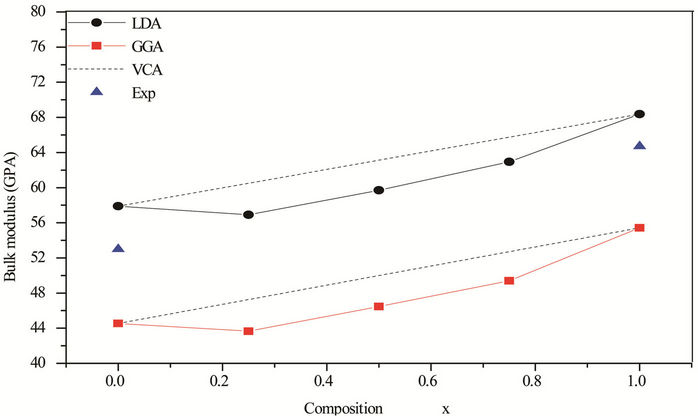
Figure 2. Composition dependence of the calculated bulk modulus within GGA (solid square) and LDA (solid circle) of ZnxCd1−xSe alloy compared with experimental (solid triangle).
values, one can note that the GGA approach underestimates the experimental values of the band gaps for all materials of interest. This is an expected result since the GGA usually underestimates the energy band gaps [37]. The GGA has a simple form which is not sufficiently flexible for accurately reproducing both exchange-correlation energy and its charge derivative.
The variation of the concentration (x) versus the value of the band structure (direct 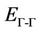 and indirect
and indirect 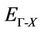 band gaps) with both LDA and GGA approximations is given in Figure 3. Afterwards this figure we notice the wide difference of direct and indirect band gaps of the composition x. has a behavior linear. The study of the polynomial function represents that our alloy has a direct gap with different concentration (0.25, 0.5 and 0.75), this alloy ZnxCd1−xSe is different compared with other alloys, stabilizes and is not subject to change.
band gaps) with both LDA and GGA approximations is given in Figure 3. Afterwards this figure we notice the wide difference of direct and indirect band gaps of the composition x. has a behavior linear. The study of the polynomial function represents that our alloy has a direct gap with different concentration (0.25, 0.5 and 0.75), this alloy ZnxCd1−xSe is different compared with other alloys, stabilizes and is not subject to change.
And obey the following variations:
ZnxCd1−xSe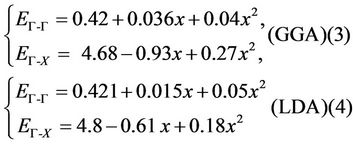

The overall bowing coefficient at each composition x measures the change in the band gap according to the formal reaction
 (5)
(5)
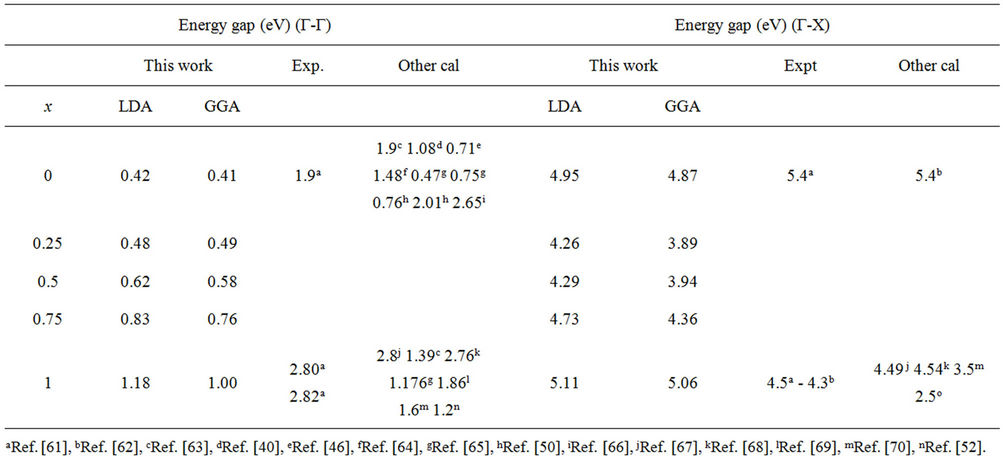
Table 3. Direct (Γ-Γ) and indirect (Γ-X) band gaps of CdSe and ZnSe and their alloy at different concentrations (all values are in eV).

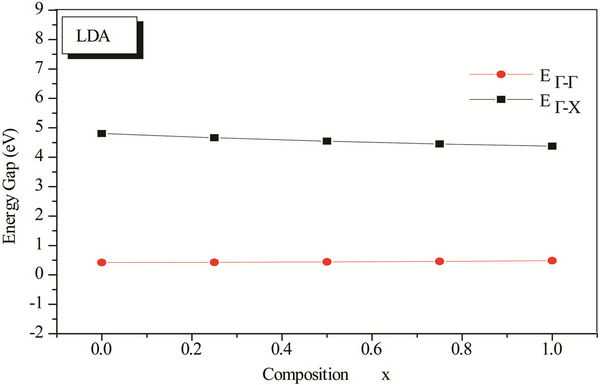
Figure 3. Energy band gap of ZnxCd1−xSe alloy as a function of Se composition using LDA and GGA approximations.
where 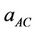 and
and  are the equilibrium lattice constants of the CdSe, ZnSe compounds and
are the equilibrium lattice constants of the CdSe, ZnSe compounds and  is the equilibrium lattice constant of the ZnxCd1−xSe alloy with the average composition x.
is the equilibrium lattice constant of the ZnxCd1−xSe alloy with the average composition x.
The physical origins of the bowing gap were investigated following the approach of Zunger and co-workers [38,39], which decompose it into three contributions:
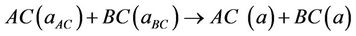 (6)
(6)
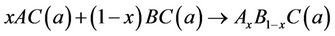 (7)
(7)
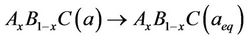 (8)
(8)
The first step measures the volume deformation (VD) effect on the bowing. The corresponding contributions bVD to the bowing parameter represents the relative response of the band structure of the binary compounds AC and BC to hydrostatic pressure, which here arises from the change of their individual equilibrium lattice constants to the alloy value a = a(x). The second contribution, the charge exchange (CE) contribution bCE, reflects the charge transfer effect which is due to the different (averaged) bonding behaviour at the lattice constant a. The last contribution, the so called “structural relaxation” (SR), measures changes in passing from the unrelaxed to the relaxed alloy by bSR. Consequently, the total bowing parameter is defined as:
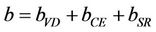 (9)
(9)
The general representation of the composition dependent band gap of the alloy in terms of the binary compounds gaps is ECdSe(aCdSe), EZnSe(aZnSe), and the total bowing parameter b is given by
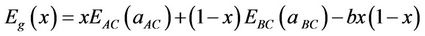 (10)
(10)
where EAC and EBC corresponds to the energy gap of ZnSe and CdSe for the ZnxCd1−xSe alloy. This allows a splitting of the total bowing b into three contributions according to
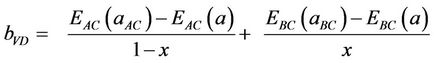 (11)
(11)
 (12)
(12)
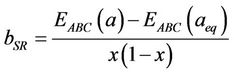 (13)
(13)
All of these energy gaps occurring in expressions (11)- (13) have been calculated for the indicated atomic structures and lattice constants.
The calculated bowing coefficients b calculated at molar fractions x = 0.25, 0.50 and 0.75 for ZnxCd1−xSe alloy are listed in Table 4 using FP-LMTO method within LDA and GGA approximations we notice that the structural relaxation effect is the smaller for the studied compositions x = 0.25, 0.50 and 0.75 and the main contribution to the band gap bowing is essentially due to the charge exchange (CE) contribution for x = 0.25 x = 0.5 and 0.75. It is clearly seen that our LDA values for total bowing parameters are better than the corresponding with in GGA. Figure 4 shows the variation of the band gap bowing versus concentration. It is shown that the optical bowing decreases slightly from 0.25 to 0.5, and beyond 0.5 it increases rapidly, to the best of our knowledge, there are no theoretical or experimental data on the band gap bowing to check our predicted results.
3.3. Effective Masses
Although the effective mass approximation is used extensively throughout the literature, the actual electron and hole effective masses for the alloys in the whole range of x, are unknown. The transport and optical phenomena usually are governed by the band structures in the immediate vicinity of the Brillouin zone center. Thus the effective mass approximation turns to be an appropriate method to make the analysis of the electronic energy band curvatures. Generally, the effective mass is a tensor with nine components, however for the much
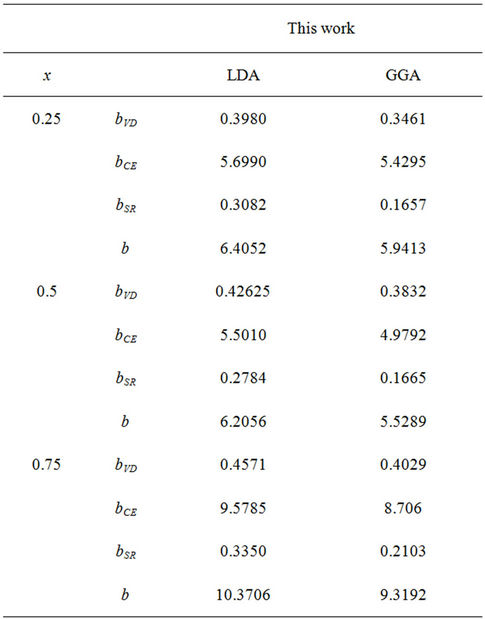
Table 4. Decomposition of optical bowing into volume deformation (VD), charge exchange (CE) and structural relaxation (SR) contributions (all values in eV).

Figure 4. Calculated band gap bowing parameter as a function of Se concentration within GGA (solid square) and LDA (solid triangle).
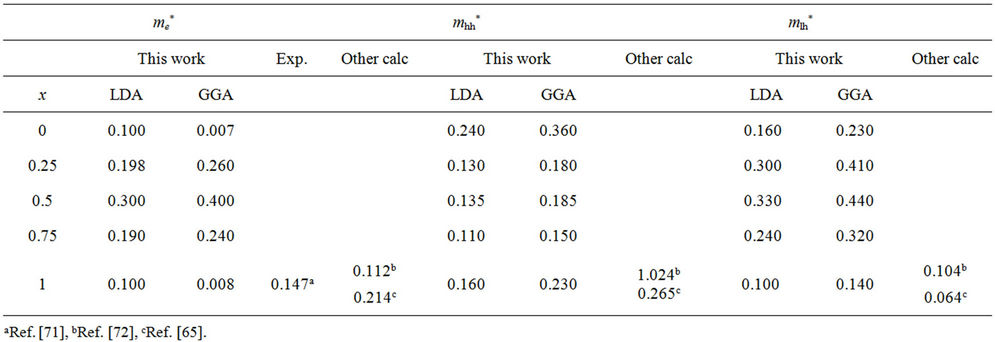
Table 5. Electron (me*), light hole (mlh*) and heavy hole (mhh*) effective masses (in units of free electron mass m0) of the ternary alloy ZnxCd1−xSe compared with the available experimental data and theoretical result.
idealized simple case, where the E-k diagram can be fitted by a parabola E = ћ2k2/2 m*, the effective mass becomes a scalar at high symmetry point in Brillouin zone. We have computed the electron effective mass at the conduction band minima (CBM) and the hole effective mass at the valence band maxima (VBM) for CdSe, ZnSe and their ternary alloys, the results of our calculations were investigated in Table 5, that shows the calculated electron and hole (heavy and light) effective masses from 0 to 1.0 for ZnxCd1−xSe alloys at point Γ of the Brillouin zone. Our results concerning the electrons, heavy holes and light hole effective mass are shown in Figure 5. From Table 5, we can outline that the calculated electron effective masses for the studied composition are much smaller, predicting a higher mobility of electrons, for all concentrations in ZnxCd1−xSe alloy, the carrier transport in this alloy should be dominated by electrons. Our calculated effective masses for ZnSe are found comparable by Baaziz et al. [72].
4. Conclusion
The (FP-LMTO) method is used to calculate the structural and electronic properties zinc-blende phase of CdSe, ZnSe and their ZnxCd1−xSe alloy within LDA and GGA approximations. We observed that GGA somewhat overestimates the experimental data on the other side are underestimated with the LDA approximation. A small deviation of the lattice constant from Vegard’s law was observed for ZnxCd1−xSe alloy. The electronic band structure is in good agreement with the experimental and other
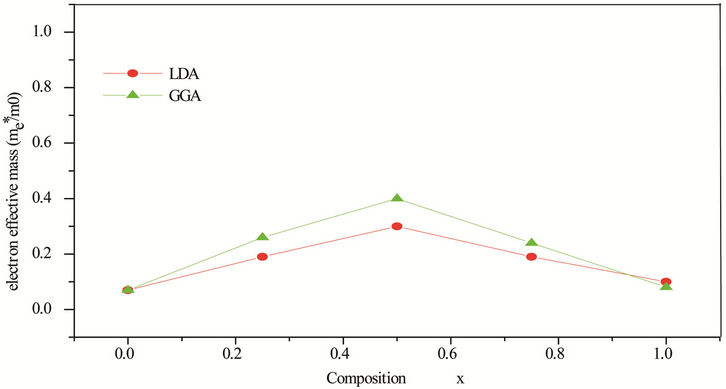
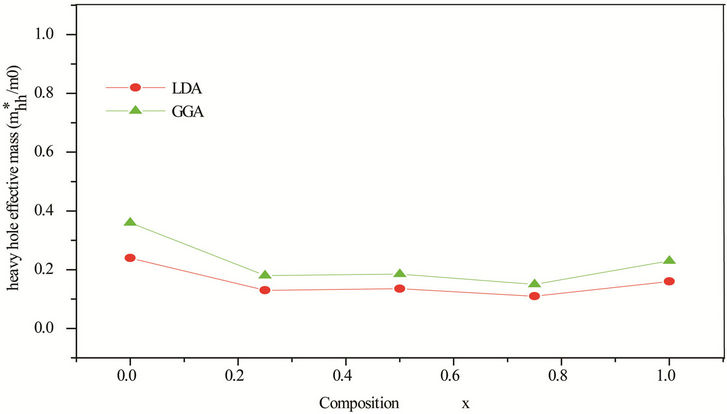
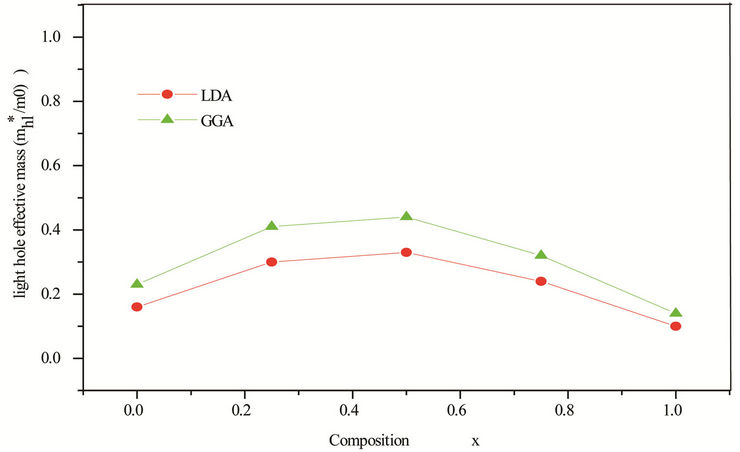
Figure 5. (a) Electron effective mass at point Γ as function of Se composition within LDA and GGA. (b) Heavy hole effective mass (in units of free electron mass m0) of Se composition within LDA and GGA. (c) Light hole effective mass at point Γ as function of Se composition within LDA and GGA.
computational work. Our results show a strong dependence of the band gap bowing factor using Zunger approach on composition. The effective masses are investigated and showed good accordance using LDA and GGA especially for electron mass.
REFERENCES
- S. Coe, W.-K. Woo, M. Bawendi and V. Bulovic, “Electroluminescence from Single Monolayers of Nanocrystals in Molecular Organic Devices,” Nature, Vol. 420, 2002, pp. 800-803. doi:10.1038/nature01217
- N. Tessler, et al., “Efficient Near-Infrared Polymer Nanocrystal Light-Emitting Diodes,” Science, Vol. 295, No. 5559, 2002, pp. 1506-1508. doi:10.1126/science.1068153
- D. Gal, G. Hodes, D. Hariskos, D. Braunger and H.-W. Schock, “Size-Quantized CdS Films in Thin Film CuInS2 Solar Cells,” Applied Physics Letters, Vol. 73, No. 21, 1998, pp. 3135-3137. doi:10.1063/1.122697
- W. U. Huynh, J. J. Dittmer and A. P. Alivisato, “Hybrid Nanorod-Polymer Solar Cells,” Science, Vol. 295, No. 5564, 2002, pp. 2425-2427. doi:10.1126/science.1069156
- V. L. Colvin, M. C. Schlamp and A. P. Alivisatos, “LightEmitting-Diodes Made from Cadmium Selenide Nanocrystals and a Semiconducting Polymer,” Nature, Vol. 370, No. 6488, 1994, pp. 354-357. doi:10.1038/370354a0
- B. O. Dabbousi, M. G. Bawendi and O. O. Rubner, “Electroluminescence from CdSe Quantum-Dot/Polymer Composites,” Applied Physics Letters, Vol. 66, No. 11, 1995, pp. 1316-1318. doi:10.1063/1.113227
- B. O’Regan and M. Grätzel, “A Low-Cost, High-Efficiency Solar Cell Based on Dye-Sensitized Colloidal TiO2 Films,” Nature, Vol. 353, No. 6346, 1991, pp. 737- 740.doi:10.1038/353737a0
- N. C. Greenham, X. Peng and A. P. Alivisatos, “Charge Separation and Transport in Conjugated Polymer/Cadmium Selenide Nanocrystal Composites Studied by Photoluminescence Quenching and Photoconductivity,” Synthetic Metals, Vol. 84, No. 2, 1997, pp. 545-546. doi:10.1016/S0379-6779(97)80852-1
- C. G. Van de Walle, “Wide-Band-Gap Semiconductors,” North Holland, Amsterdam, 1993.
- J. K. Jaiswal, et al., “Long-Term Multiple Color Imaging of Live Cells Using Quantum Dot Bioconjugates,” Nature Biotechnology, Vol. 21, No. 1, 2003, pp. 47-51. doi:10.1038/nbt767
- H. Jeon, J. Ding, W. Patterson, A. V. Nurmikko, W. Xie, D. C. Grillo, M. Kobayashi and R. L. Gunshor, “BlueGreen Injection Laser Diodes in (Zn, Cd )Se/ZnSe Quantum Wells,” Applied Physics Letters, Vol. 59, No. 27, 1991, pp. 3619-3621. doi:10.1063/1.105625
- Y. Eisen and A. Shor, “CdTe and CdZnTe Materials for Room-Temperature X-Ray and Gamma Ray Detectors,” Journal of Crystal Growth, Vol. 184-185, No. 1-4, 1998, pp. 1302-1312. doi:10.1016/S0022-0248(98)80270-4
- L. Hannachi and N. Bouarissa, “Electronic Structure and Optical Properties of CdSexTe1−x Mixed Crystals,” Superlattices and Microstructures, Vol. 44, No. 6, 2008, pp. 794-801. doi:10.1016/j.spmi.2008.09.013
- F. Z. Amir, K. Clark, E. Maldonado, W. P. Kirk, J. C. Jiang, J. W. Ager, K. M. Yu and W. Walukiewicz, “Epitaxial Growth of CdSexTe1−x Thin Films on Si(100) by Molecular Beam Epitaxy Using Lattice Mismatch Graded Structures,” Journal of Crystal Growth, Vol. 310, No. 6, 2008, pp. 1081-1087. doi:10.1016/j.jcrysgro.2007.12.055
- M. Durandurdu, “Pressure-Induced Phase Transition in Wurtzite ZnS: An ab Initio Constant Pressure Study,” Journal of Physics and Chemistry of Solids, Vol. 70, No. 3-4, 2009, pp. 645-649. doi:10.1016/j.jpcs.2009.01.008
- S. Cui, H. Hu, W. Feng, X. Chen and Z. Feng, “PressureInduced Phase Transition and Metallization of Solid ZnSe,” Journal of Alloys and Compounds, Vol. 472, No. 1-2, 2009, pp. 294-298. doi:10.1016/j.jallcom.2008.04.052
- K. Wright and J. D. Gale, “Interatomic Potentials for the Simulation of the Zinc-Blende and Wurtzite Forms of ZnS and CdS: Bulk Structure, Properties, and Phase Stability,” Physical Review B, Vol. 70, 2004, Article ID: 035211. http://link.aps.org/doi/10.1103/PhysRevB.70.035211
- S.-H. Wei and S. B. Zhang, “Structure Stability and Carrier Localization in Cdx (x = S, Se, Te) Semiconductors,” Physical Review B, Vol. 62, No. 11, 2000, pp. 6944-6947. doi:10.1103/PhysRevB.62.6944
- Y. Al-Douri, “The Pressure Effect of the Bulk Modulus Seen by the Charge Density in Cdx Compounds,” Materials Chemistry and Physics, Vol. 78, No. 3, 2003, pp. 625-629. doi:10.1016/S0254-0584(02)00308-5
- K. Bouamama, P. Djemia, N. Lebga and K. Kassali, “Ab Initio Calculation of the Elastic Properties and the Lattice Dynamics of the ZnxCd1−xSe Alloy,” Semiconductor Science and Technology, Vol. 24, 2009, Article ID: 045005. doi:10.1088/0268-1242/24/4/045005
- N. Benosman, N. Amrane and H. Aourag, “Calculation of Electronic and Optical Properties of Zinc-Blende ZnxCd1−xSe,” Physica B, Vol. 275, No. 12, 2000, pp. 316- 327. doi:10.1016/S0921-4526(99)00396-8
- Y. D. Kim, M. V. Klein, S. F. Ren, Y. C. Chang, H. Luo, N. Samarth and J. K. Furdyna, “Optical Properties of Zinc-Blende CdSe and ZnxCd1−xSe Films Grown on GaAs,” Physical Review B, Vol. 49, No. 11, 1994, pp. 7262-7270. doi:10.1103/PhysRevB.49.7262
- N. Samarth, H. Luo, J. K. Furdyna, R. G. Alonso, Y. R. Lee, A. K. Ramdas, S. B. Qadri and N. Otsuka, “Molecular Beam Epitaxy of Zn1−xCdxSe Epilayers and ZnSe/ Zn1−xCdxSe Super Lattices,” Applied Physics Letters, Vol. 56, No. 12, 1990, pp. 1163-1166. doi:10.1063/1.102551
- K. Suzuki and S. Adachi, “Optical Constants of CdxZn1−xSe Ternary Alloys,” Journal of Applied Physics, Vol. 83, No. 2, 1998, pp. 1018-1022. doi:10.1063/1.366791
- S. Savrasov and D. Savrasov, “Full-Potential LinearMuffin-Tin-Orbital Method for Calculating Total Energies and Forces,” Physical Review B, Vol. 46, No. 19, 1992, pp. 12181-12195. doi:10.1103/PhysRevB.46.12181
- W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review A, Vol. 140 , No. 4A, 1965, pp. A1133-A1138. doi:10.1103/PhysRev.140.A1133
- 2007. http://www.physics.ucdavis.edu/_savrasov/S
- P. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Physical Review B, Vol. 136, No. 3B, 1964, pp. 864-971. doi:10.1103/PhysRev.136.B864
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review B, Vol. 45, No. 23, 1992, pp. 13244-13249. doi:10.1103/PhysRevB.45.13244
- J. P. Perdew, S. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- P. Blochl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223- 16233. doi:10.1103/PhysRevB.49.16223
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences, Vol. 30, No. 9, 1944, pp. 244-247. doi:10.1073/pnas.30.9.244
- A. Mokhtari and H. Akbarzadeh, “Electronic and Structural Properties of β-Be3N2,” Physica B, Vol. 324, No. 1-4, 2002, pp. 305-331. doi:10.1016/S0921-4526(02)01416-3
- L. Vegard, “Formation of Mixed Crystals by Solid-Phase Contact,” Journal of Physics, Vol. 5, 1921, pp. 393-395.
- B. Jobst, D. Hommel, U. Lunz, T. Gerharda and G. Landwehr, “E0 Band-Gap Energy and Lattice Constant of Ternary Zn1−xMgxSe as Functions of Composition,” Applied Physics Letters, Vol. 69, No. 1, 1996, pp. 97-100. doi:10.1063/1.118132
- F. El-Haj Hassan and H. Akdarzadeh, “First-Principles Investigation of BNxP1–x, BNxAs1–x and BPxAs1–x Ternary Alloys,” Materials Science and Engineering, Vol. 121, No. 1-2, 2005, pp. 171-178. doi:10.1016/j.mseb.2005.03.019
- P. Dufek, P. Blaha and K. Schwarz, “Applications of Engel and Vosko’s Generalized Gradient Approximation in Solids,” Physical Review B, Vol. 50, No. 11, 1994, pp. 7279-7283. doi:10.1103/PhysRevB.50.7279
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, “Special Quasirandom Structures,” Physical Review Letters, Vol. 65, No. 3, 1990, pp. 353-356. doi:10.1103/PhysRevLett.65.353
- S.-H. Wei, L. G. Ferreira, J. E. Bernard and A. Zunger, “Electronic Properties of Random Alloys: Special QuaSirandom Structures,” Physical Review B, Vol. 42, No. 15, 1990, pp. 9622-9649. doi:10.1103/PhysRevB.42.9622
- O. Madelung and L. Bornstein, “Numerical Data and Functional Relationship in Science and Technology, New Series Group III,” Vol. 17, Springer-Verlag, Berlin, 1982.
- E. Deligoz, K. Colakoglu and Y. Ciftci, “Elastic, Electronic, and Lattice Dynamical Properties of CdS, CdSe, and CdTe,” Physica B: Physics of Condensed Matter, Vol. 373, No. 1, 2006, pp. 124-130. doi:10.1016/j.physb.2005.11.099
- L. H. Thomas, “The Calculation of Atomic Fields,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 23, No. 5, 1927, pp. 542-548. doi:10.1017/S0305004100011683
- M. Born and J. R. Oppenheimer, “Zur Quanttheorie der Moleculen,” Annals of Physics, Vol. 87, No. 20, 1927, pp. 457-484. doi:10.1002/andp.19273892002
- P. K. Lam, M. L. Cohen and G. Martinez, “Analytic Relation between Bulk Moduli and Lattice Constants,” Physical Review B, Vol. 35, No. 17, 1987, pp. 9190-9194. doi:10.1103/PhysRevB.35.9190
- Landolt-Bornstein, “Numerical Data and Functional Relationships in Science and Technology,” Crystal and Solid State Physics, Vol. 22, Springer-Verlag, Berlin, 1987.
- Z. Nourbakh, “Structural, Electronic and Optical Properties of Znx and Cdx Compounds (x = Se, Te and S) under Hydrostatic Pressure,” Journal of Alloys and Compounds, Vol. 505, No. 2, 2010, pp. 698-711. doi:10.1016/j.jallcom.2010.06.120
- M.-Z. Huang and W. Y. Ching, “Calculation of Optical Excitations in Cubic Semiconductors, I: Electronic Structure and Linear Response,” Physical Review B, Vol. 47, No. 15, 1993, pp. 9449-9463. doi:10.1103/PhysRevB.47.9449
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, “Energy Band Gaps and Lattice Parameters Evaluated with the Heyd-Scuseria-Ernzerh of Screened Hybrid Functional,” Journal of Chemical Physics, Vol. 123, 2005, Article ID: 174101. doi:10.1063/1.2085170
- O. Zakharov, A. Rubio, X. Blase, M. L. Cohen and S. G. Loui, “Quasiparticle Band Structures of Six II-VI Compounds: ZnS, ZnSe, ZnTe, CdS, CdSe, and CdTe,” Physical Review B, Vol. 50, No. 15, 1994, pp. 10780-10787. doi:10.1103/PhysRevB.50.10780
- M. B. Kanoun, W. Sekkal, H. Aourag and G. Merad, “Molecular Dynamics Study of the Structural, Elastic and Thermodynamic Properties of Cadnium Telluride,” Physics Letters A, Vol. 272, No. 1-2, 2000, pp. 113-118. doi:10.1016/S0375-9601(00)00403-5
- N. Benkhettou, D. Rached, B. Soudini and M. Driz, “HighPressure Stability and Structural Properties of CdS and CdSe,” Physica Status Solidi B, Vol. 241, No. 1, 2004, pp. 101-107. doi:10.1002/pssb.200301907
- S. Ouendadjia, S. Ghemida, H. Meradjia and F. El-Haj Hassan, “Theoretical Study of Structural, Electronic, and Thermalproperties of CdS, CdSe and CdTecompounds,” Computational Materials Science, Vol. 50, No. 4, 2011, pp. 1460-1466. doi:10.1016/j.commatsci.2010.11.035
- B. H. Lee, “Pressure Dependence of the Second-Order Elastic Constants of ZnTe and ZnSe,” Journal of Applied Physics, Vol. 41, No. 7, 1970, pp. 2988-2990. doi:10.1063/1.1659350
- J. C. Jamieson and H. H. Demarest, “A Note on the Compression of Cubic ZnS,” Journal of Physics and Chemistry of Solids, Vol. 41, No. 9, 1980, pp. 963-964. doi:10.1016/0022-3697(80)90101-8
- P. Y. Yu and M. Cardona, “Fundamentals of Semiconductors Physics and Materials Properties,” Springer-Verlag, Berlin, 2001. doi:10.1007/978-3-642-00710-1
- R. Khenata, A. Bouhemadou, M. Sahnoun, H. R. Ali, H. Baltache and M. Rabah, “Elastic, Electronic and Optical Properties of ZnS, ZnSe and ZnTe under Pressure,” Computational Materials Science, Vol. 38, No. 1, 2006, pp. 29-38. doi:10.1016/j.commatsci.2006.01.013
- S.-G. Lee and K. J. Chang, “First Principles Study of the Structural Properties of MgS, MgSe, ZnS and ZnSe Based Superlattices,” Physical Review B, Vol. 52, No. 3, 1995, pp. 1918-1925. doi:10.1103/PhysRevB.52.1918
- B. N. Brahmi, A. E. Merad and M. R. Boufatah, “Proprietes Electronique du Znx (x = S, Se, Te) via des Appromaximations Quantiques: Etude par la Fonctionnelle de la Densite,” Matériaux et Composants Electroniques, CNPA VIII, Béjaia, 11-13 Novembre 2008.
- F. Benkabou, H. Aourag and M. Certier, “Atomistic Study of Zinc-Blends CdS, CdSe, ZnS, and ZnSe from Molecular Dynamics,” Materials Chemistry and Physics, Vol. 66, No. 1, 2000, pp. 10-16. doi:10.1016/S0254-0584(00)00239-X
- [61] M. L. Cohen, “Calculation of Bulk Moduli of Diamond and Zinc-Blende Solids,” Physical Review B, Vol. 32, No. 12, 1985, pp. 7988-7991. doi:10.1103/PhysRevB.32.7988
- [62] I. M. Tsidilkovski, “Band Structure of Semiconductors,” Elsevier Science & Technology Books, Amsterdam, 1982.
- [63] M. Cardona, “Fundamental Reflectivity Spectrum of Semiconductors with Zinc-Blende Structure,” Journal of Applied Physics, Vol. 32, No. 10, 1961, pp. 2151-2155 doi:10.1063/1.1777034
- [64] X. J. Chen, X. L. Hua, J. S. Hu, J.-M. Langlois and W. A. Goddard III., “Band Structures of II-VI Semiconductors Using Gaussian Basis Functions with Separable ab Initio Pseudopotentials: Application to Prediction of Band Offsets,” Physical Review B (Condensed Matter), Vol. 53, No. 3, 1996, pp. 1377-1387. doi:10.1103/PhysRevB.53.1377
- [65] R. R. Reddy, K. R. Gopal, K. Narasimhulu, L. S. S. Reddy, K. R. Kumar, G. Balakrishnaiah and M. R. Kumar, “Interrelationship between Structural, Optical, Electronic and Elastic Properties of Materials,” Journal of Alloys and Compounds, Vol. 473, No. 1-2, 2009, pp. 28-35. doi:10.1016/j.jallcom.2008.06.037
- [66] M. Ameri, D. Rached, M. Rabah, R. Khenata, N. Benkhettou, B. Bouhafs and M. Maachou “Structural and Electronic Properties Calculations of BexZn1−xSe Alloy,” Materials Science in Semiconductor Processing, Vol. 10, No. 1, 2007, pp. 6-13. doi:10.1016/j.mssp.2007.01.003
- [67] Y. Duan and M. Jungen, “Electronic Structural and Magnetic Properties of Cadmium Chalcogenide Beryllosilicate Sodalites,” European Physical Journal B, Vol. 2, No. 2, 1998, pp. 183-190. doi:10.1007/s100510050239
- [68] Y. Al-Douri. H. Abid and H. Aourag, “Correlation between the Bulk Modulus and the Transition Pressure in Semiconductors,” Materials Letters, Vol. 59, No. 16, 2005, pp. 2032-2034. doi:10.1016/j.matlet.2005.02.011
- [69] J. R. Chelikowsky and M. L. Cohen, “Nonlocal Pseudopotential Calculations for the Electronic Structure of Eleven Diamond and Zinc-Blende Semiconductors,” Physical Review B, Vol. 14, No. 2, 1976, pp. 556-582. doi:10.1103/PhysRevB.14.556
- [70] F. El-Haj Hassan, S. J. Hashemifar and H. Akbarzadeh, “Density Functional Study of Zn1−xMgxSeyTe1−y Quaternary Semiconductor Alloys,” Physical Review B, Vol. 73, No. 19, 2006, pp. 195-202. doi:10.1103/PhysRevB.73.195202
- [71] C. Narayana, V. J. Nesamony and A. L. Ruoff, “Phase Transformation of BeS and Equation-of-State Studies to 96 GPa,” Physical Review B, Vol. 56, No. 22, 1997, pp. 14338- 14343. doi:10.1103/PhysRevB.56.14338
- [72] H. W. Holscher, A. Nothe and C. Uihlein, “Investigation of Band Masses and g Values of ZnSe by Two-Photon Magnetoabsorption,” Physical Review B, Vol. 31, No. 4, 1985, pp. 2379-2387. doi:10.1103/PhysRevB.31.2379
- [73] H. Baaziz, Z. Charifi, F. El-Haj Hassan, S. J. Hashemifar and H. Akbarzadeh, “FP-LAPW Investigations of Zn1–xBexS, Zn1–xBexSe and Zn1–xBexTe Ternary Alloys,” Physica Status Solidi B, Vol. 243, No. 6, 2006, pp. 1296-1305. doi:10.1002/pssb.200541481
NOTES
*Corresponding author.

