Circuits and Systems
Vol.07 No.09(2016), Article ID:68083,12 pages
10.4236/cs.2016.79184
An Improved Hybrid Space Vector PWM Technique for IM Drives
P. Muthukumar1,2, P. Melba Mary3, S. Jeevananthan4
1Sree Sastha Institute of Engineering and Technology, Chennai, India
2Anna University, Chennai, India
3VV College of Engineering, Tisaiyanvilai, India
4Pondicherry Engineering College, Pondicherry University, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2016; accepted 3 May 2016; published 8 July 2016
ABSTRACT
In this paper, an improved hybrid space vector pulse width modulation (HSVPWM) technique is proposed for IM (induction motor) drives. The basic principle involved in the proposed random pulse width modulation (RPWM) cuddled SVPWM is amalgamating the pre-calculated switching timings for various sections of hexagonal space vector boundary and the random selection of carrier between two triangular signals, in order to disband acoustic switching noise spectrum with improved fundamental component. The arbitrary selection between triangular carriers, which is decided by digital signal states (Low or High) of the linear feedback shift register (LFSR) based pseudo random binary sequence (PRBS) generator. The SVPWM offers a control degree of freedom in terms of positioning of vectors inside every sampling interval and hence it has six possible variants of the voltage vectors arrangements in each sector. The developed HSVPWM is thoroughly analyzed in using the MATLAB® based simulation for all SVPWM variants. From the simulation and experimental results viz. harmonic spectrum, harmonic spread factor (HSF), total harmonic distortion (THD) etc., and the superiority of the proposed scheme such as better utilization of DC bus and the randomization of the harmonic power are evidenced. For the practical implementation, Xilinx XC3S500E FPGA device has been used.
Keywords:
Harmonic Spread Factor, Hybrid Space Vector Pulse Width Modulation, Pseudo Random Binary Sequence, Random Pulse Width Modulation

1. Introduction
The main aim of any modulation technique employed in voltage source inverters (VSIs) is to obtain variable output having a maximum fundamental component with minimum distortion. In a sinusoidal pulse width modulation (SPWM), a sinusoidal reference signal at desired output frequency is compared with a triangular waveform to generate the required duty cycles. The drawback of this technique is that it generates a fundamental term with limited amplitude, a significant amount of undesired carrier frequency harmonics and increased switching losses [1] whereas the advantage is being larger dead band between the fundamental and the first dominant harmonics. These high switching frequency schemes ease the filtering effort but a low frequency switching scheme which inherently suppresses the lower order harmonics can offer reduced switching losses.
Space vector pulse width modulation (SVPWM) is a method of pre-calculation of switching the timing instants for various sections of target output which has options in terms of positioning the active vectors inside every sampling interval [2] [3] . The SVPWM claims reduced distortion and enhanced the fundamental component when compared with the SPWM. The space vector theory, which involves rotating reference and hexagonal boundary (and triangular sectors) offers a control degree of freedom in selecting in active vectors and null vectors [4] [5] . The performance of the SVPWM technique is considerably influenced by selection of null vectors and their positioning [6] . These multiple options in selecting the null vectors and forming a combined sequence with active vectors render six different space vector patterns [7] [8] . Due to the deterministic PWM/SVPWM switching of the inverters, the motor generates an unpleasant acoustic switching noise and a mechanical vibration [9] and the best way to reduce the audible switching noise radiated from the induction motor is to increase the switching frequency up to 20 kHz. By using such method, noise problem can be solved, on the other hand it increases the switching losses of the inverter [10] .
Random PWM (RPWM) methods have attracted attention from 1987 as a solution to the above problem. In a typical RPWM, the duty cycle is computed by comparing the sinusoidal reference wave with the randomly composed triangular carrier using two triangular waves each of the same has fixed frequency, but of opposite the phase [11] . These undeterministic PWM methods spread the harmonic power as demanded by modern drives and their influential variation in fundamental term and THD are negligible. More numbers of RPWM schemes have been investigated, which differ in how the randomness is incorporated in the carrier signal. A pseudo random triangular carrier modulation method and its harmonic spread effect have been discussed [11] . In addition, Chaos-based PWM strategies have also been discussed, whereas it utilizes a chaotic changing switching frequency to spread the harmonics continuously to a wideband area, so that the peak harmonics could be reduced greatly [12] .
A discontinuous PWM method has exhibited better performance with higher modulation range which is mandatory for high power applications [13] . Field programmable Gate Arrays (FPGAs) have become one of the most popular implementation media for digital circuits, and their preamble in 1984. The key to success of FPGAs is their programmability which allows any circuit to be instantly composed out by appropriate programming [14] . Even though the SVPWM patterns offer the major requirements of the drives and conceptually suite with modern speed control methods, clustering of harmonics around a specific frequency is objectionable. RPWM methods performs well in terms of secondary issues like spreading the harmonic power etc. while the primary issues related parameters like improved fundamental, reduced THD and higher dead band separation for harmonics are not appreciable. In this paper, a modified SVPWM strategy is developed by using FPGA which performs similar to conventional SVPWM in primary issues but with improved secondary issues like harmonic spreading effect.
2. Space Vector Modulation Switching Patterns
Space vector pulse width modulation is a digital PWM method, in which, the duty cycles of gating pulses are pre-calculated for every sections of target output cycle [5] [6] . At any instant in a particular sector, two vectors need to be participated in variable timing intervals to establish the target vector as indicated in Figure 1. The effective switching instants are calculated as follows.
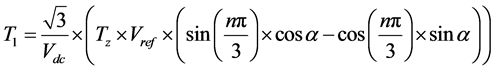 (1)
(1)
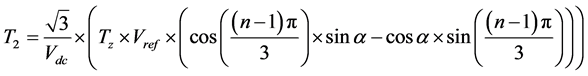 (2)
(2)
Figure 1. Principle of SVPWM.
where, T1, T2 and T0 are computed switching instants for the lagging, leading and zero switching vectors, “n” is the sector number (Sectors 1 to 6), Tz is sampling time, fc is switching frequency and α is the instantaneous phase angle of Vref (0˚ ≤ α ≤ 360˚). The freedom in space vector modulation (SVM) is the choice of formulating the switching patterns [6] . The basic idea behind the any SVM pattern is the average voltage resulted in a sampling interval is same, but if the contributing vectors are switched for their computed times (T1 and T2) with appropriate null vector and the sequence. In contrary, the different patterns not only offer merits like unit transition, reduced switching losses, ease of implementation etc. but also performance differences in terms of fundamental component value and THD. The clues of the patterns’ variation are detailed below.
The choice of the zero vectors―(i) contribution of V7 (111) or V0 (000) or both for pattern formation, (ii) sequencing of the vectors (clockwise reference vector rotation and anti-clockwise reference vector rotation) and arrangement of leading, lagging and null vectors, (iii) and splitting of the duty cycles of the vectors without introducing additional commutations. Based on the above clues, six patterns are formulated. It is worth noting that according to the theory of SVM, the reference vector is contributed just by active vectors, not by null vectors. The involvement of null vectors may facilitate the digital implementation and also helps in solving few practical circuit complications. Avoidance of the null vectors may create a problem in inverter bridges that use isolation circuits such as bootstrap. The reason is that the lower leg of the inverter is switched on or off for extended periods of time. Pattern I: An unique switching pattern is followed for each sector and can be summarized as V0 (000), V1 (100), V2 (110), V7 (111), V7 (111), V2 (110), V1 (100), V0 (000) for sector 1. Where, V1 and V2 (V1 + 60˚) are the forming (contributing) vectors in the sector 1. For the consecutive sector (Sector 2) the respective contributing vectors, V2 and V3 are used in place of V1 and V2. Pattern II: This pattern is similar to pattern I, but only the null vector V0 is involved in all sectors along with two active vectors. Pattern III: This pattern is similar to pattern II, but the null vector V7 is engaged instead of V0. Pattern IV: This pattern has two different vector sequences for odd numbered (1, 3, 5) and even numbered (2, 4, 6) sectors. With the contribution of vectors, odd sectors and even sectors use V7 and V0 as null vectors respectively. Pattern V: In this pattern, the null vector assignment is swapped while comparing to the pattern IV. That is, V0 is considered for odd sectors and V7 for even sectors. Pattern VI: This pattern is similar to pattern II, but the assignment of active vectors V1 and V2 are swapped.
3. Problem Formulation
The PWM techniques can be broadly classified as deterministic PWM schemes and non-deterministic PWM schemes. The conventional PWM schemes viz. SPWM, SVPWM, selective harmonic elimination PWM (SHEPWM) etc. are examples for deterministic PWM schemes. The RPWM schemes are non-deterministic PWM schemes. The deterministic PWM schemes are operated at constant switching frequency in a modern drive system [1] - [5] . In any deterministic PWM with carrier frequency, fc (say 1.5 kHz), the harmonic spectrum possesses the clustered harmonics at its multiples (2fc, 4fc, 6fc etc.) as shown in Figure 2.
Figure 2. Output voltage harmonic spectrum of SPWM.
The acoustic noise emitted by the motor is very annoying under this condition since the majority harmonics comes within the audible range (20 Hz - 20 kHz). These clustered harmonic spectra will produce acoustic noise, electromagnetic interference (EMI), mechanical vibration and hence paves a possibility of physical damage to the rotor. The best way to reduce the audible switching noise is radiated from the induction motor is to increase the PWM switching frequency up to 18 kHz. Such a method can solve the noise problem but increases the switching loss of the inverter [12] . In general, the 1 - 10 kHz range is the region of the greatest annoyance for human listeners. Unfortunately, this range may coincide with the switching frequency of the VSI quite often. Hence it is important that the acoustic noise radiated from the induction motor, with a frequency below 10 kHz should be reduced. In recently, to overcome this problem, a new host of techniques called RPWM has been proposed. The basic requirement of applications, which demands acoustic noise and vibration free working in harmonic spectrum involving more number of harmonics none having dominant magnitude (say > 5% of fundamental) rather than the spectrum of less number of dominant harmonics. This feature is otherwise known as spreading of harmonic power. RPWM methods contribute to dispersing of harmonics with same (range of) switching frequency as that of deterministic PWM methods. The RPWM technique is operating at variable switching frequency. By selecting the carrier triangle wave in a random manner, the above said problems are mitigated as understood from Figure 3.
All the previous attempts in changing the reference wave were towards the fundamental enhancement and THD reduction. The reformation of harmonic spectrum like spreading the harmonic power must be done through carrier modification/randomization. The recent solution for above said problems is RPWM, where switching frequency is selected within the audible range (hence reduced switching losses) with an intelligent randomness so that no objectionable audio noise is produced.
4. Proposed Hybrid Scheme
An ingenious PWM schemes, which amalgamates the features of SVPWM and RPWM is the need of any modern ac drive system. Conceptually the SVM suggests six different references (analog equivalent) for the better most of THD and the enhanced fundamental. It does not offer any guidance on carrier selection and suggests the usage of conventional triangular carrier. Opportunely, the randomness addition in the RPWM is in carrier wave and restricted within the carrier cycle. This paves the way to amalgamate the random carrier with the SVPWM irrespective of the pattern preference.
The implementation accuracy of any computation intensive PWM largely depends on the implementation platform and the algorithm used. The proposed hybrid SVPWM (HSVPWM) adds both timing computation and carrier randomness to its complexity, and demands great care in implementation. The implementation of the HSVPWM is done with the help of an architecture as shown in Figure 4. The HSVPWM architecture consists of three functional blocks namely, SVM reference generator block, carrier generation and selection block, and pulse generation block. The SVM reference generator block has the timing equations and a reference position in incremental mechanism. For every incremental position the instants of active and null vectors are computed and used for forming three-phase references. In the carrier generation and selection block, normal triangular carrier (+fc) and inverted triangular carrier of same frequency (−fc) are given as input to the 2:1 multiplexer. Choice of triangle called winning triangle depends up on the output of the LFSR based 8 bit random bit generator. The
Figure 3. Output voltage harmonic spectrum of RPWM.
Figure 4. Proposed HSVPWM method.
pulse generation block compares the references with the randomized carrier and generates the pulses for the six switches of VSI. In case the output is “1” then the winning triangle is +fc triangle otherwise the winning triangle is −fc triangle as shown in Figure 5. This characteristic makes more continuous distribution.
In the carrier generation and selection block, normal triangular carrier (+fc) and inverted triangular carrier of same frequency (−fc) are given as input to the 2:1 multiplexer. Choice of triangle called winning triangle depends up on the output of the LFSR based 8 bit random bit generator. The pulse generation block compares the references with the randomized carrier and generates the pulses for the six switches of VSI. In case the output is
Figure 5. Generation of random triangular carrier.
“1” then the winning triangle is +fc triangle otherwise the winning triangle is −fc triangle as shown in Figure 5. This characteristic makes more continuous distribution.
5. Discussion of Simulation Results
A simulation study is carried out using MATLAB 7.9b software with ode23tb solver. Conventional simulation study for the kind of calculation involves understanding the various waveforms, harmonic study (fundamental and other harmonics) and THD along with spectrum. Another performance parameter harmonic spread factor is a simple quality indicator would be useful for evaluating the harmonic spread effect of the random PWM scheme. The factor is named as harmonic spread factor (HSF) and uses the concept of statistical deviation. The HSF [10] [11] is defined as follows:
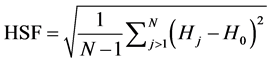 (3)
(3)
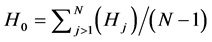 (4)
(4)
where, “Hj” is amplitude of jth harmonics, “H0” is average value of all “N − 1” harmonics. The HSF quantifies the harmonic spectra spread effect of any PWM scheme and it should be small. For ideal flat spectra of white noise, the HSF would be zero. A theoretical comparison of line to line voltage performance indices are presented in for dc bus voltage Vdc = 415 V, fundamental frequency f1 = 50 Hz and average switching frequency fc = 1.5 kHz with the inverter feeding a 0.75 kW, 415 V, 50 Hz, three-phase squirrel cage induction motor. The switches are considered to be ideal. The simulation results of the harmonic spectra for pattern I of HSVPWM (Ma = 0.8) is given in Figure 6.
The performance parameters (fundamental voltage, THD and HSF) are carried out by using FFT window in MATLAB simulation tool with one cycle of line to line voltage. Table 1 and Table 2 show that all the performance assessment of RPWM and all the patterns of SVPWM, HSVPWM. From the assessment, SVPWM pattern I contributed well while compared with the other patterns. But pattern II of the SVPWM has given very low fundamental because of poor dc bus utilization. Usually, randomness effects of the SVPWM patterns are low when compared with the superimposed RPWM which is mainly designed to disperse the predominant harmonics. From the view of HSF, the performance of SVPWM pattern I is good above the linear modulation; But RPWM is better where the modulation index range is in between 0.2 to 0.8. From the table, fundamental component of the RPWM is low when compared with the SVPWM pattern I for all the levels of modulation indices, But while comparing other patterns, RPWM has given reasonably good results for higher linear modulation indices (Ma = 0.8 to 1.0). The SVPWM higher order patterns (3, 4, 5 and 6) have performed similarly not better than the pattern I and not lesser than the pattern II. Figure 7 and Figure 8 show the convenient three dimensional graphical representation of the fundamental and THD of all the methods. From the representation, while increasing the modulation indices, fundamental component also increases and the value of THD decreases.
Figure 9 shows fruitful three dimensional graphical line representation of the significant HSF for all the methods. After the progress of the HSVPWM patterns, the fundamental value and the THD of the HSVPWM patterns
Figure 6. Line voltage spectra of HSVPWM.
Figure 7. Fundamental assessment.
Figure 8. THD assessment.
Figure 9. HSF assessment.
Table 1. Fundamental and THD assessment of SVPWM, RPWM and HSVPWM.
Table 2. HSF assessment of SVPWM, RPWM and HSVPWM.
in all the modulation indices are almost equal to SVPWM patterns. But amazingly the HSF of the HSVPWM patterns (except pattern II) are superimposed when compared to the existing SVPWM and RPWM schemes. For higher linear modulation indices (Ma = 0.8 to 1.0), HSVPWM pattern I has given a higher harmonic spreading effects(less HSF) when compared with the other HSVPWM patterns. But for lesser than 0.8 modulation indices the pattern I is less performing while comparing with the higher order HSVPWM patterns (3 to 6).
The superlative values of performance indices are underlined in Table 1 and Table 2. The improvements of the HSVPWM are clearly depicted in Table 1 and Table 2. By comparing the simulation results, the proposed HSVPWM not only afford the better performance in terms of fundamental voltage and THD than conventional SVPWM and RPWM, but also provide less harmonic spread factor which results in reduced acoustic noise. In comparison, Table 3 shows that the percentage of improvement of the HSVPWM (pattern I) is better than the SVPWM (pattern I) and RPWM. For modulation index 1.0 HSF improvement of the HSVPWM 20.29% more than the SVPWM and 23.26% is better than the RPWM
Fundamental improvement of HSVPWM 0.44% is more than the SVPWM and 28.44% more than the RPWM for modulation index 1.0. In HSVPWM, 0.23% of the THD has been decreased when compared with SVPWM and 24.88% decreased when compared with RPWM for the modulation index 1.0. Table 4 represents, noticeable dominating harmonic orders affecting the performance of the inverter fed drives system. The clustered of harmonics at its multiples (2fc = order 62, 58 and 56) are existing in the harmonic spectrum of the SVPWM and RPWM (2fc = order 60), whereas these are having less than 5% of the magnitude in HSVPWM.
6. Discussion on FPGA Synthesis Results
The recent developments in the field of VLSI made FPGAs as one of the major components in high performance processors especially in the area of power conversion utilities [14] . The VHDL has been used to design the proposed
Table 3. Percentage of improvement of HSVM.
Table 4. Dominating harmonic order and their magnitude.
method and the synthesis results have been acquired from Xilinx project navigator tool. The XC3S500E-5fg320, 90 nm low cost FPGA device is used for real time exploitation. A 50 MHz board clock has been used for sequential circuit design. In this work, 16% of look up tables are utilized. 15% DSP based 18x18 multipliers are used for development of carrier and reference waves. A Xilinx power estimator tool is used to estimate the power analysis. In this scheme, dissipation of the static power is 78 mW and the Dynamic power is 32 mW. Total power dissipated by FPGA device is 110 mW. This power analysis has been taken for typical process with commercial grade, ambient temperature is 25˚C and Vccint voltage is 1.2 V.
7. Experimental Results
To validate the analysis and simulations in the previous sections, a laboratory experimental setup has been assembled as shown in Figure 10. The set-up consists of a 0.75 kW, 415 V, 50 Hz three-phase squirrel cage induction machine fed from a 2 kW intelligent power module based IGBT inverter. Spartan3E- XC3S500E FPGA is used as the controller platform. A dead time of 2.7 µ seconds is inserted between the switches of the same inverter leg in order to ensure smooth transition of the switching states of the inverter shown in Figure 11. In both the conventional and proposed schemes, the tests are carried out with the 50 Hz fundamental frequency of the inverter voltage. Figure 12 represents the Yokogawa precision power analyzer window for measuring the line to line voltage and line current of the proposed HSVPWM scheme. In comparing the simulation results with experimental results clearly depicts that both results are very similar, and harmonic spectra spread effect is most excellent in the hybrid scheme as shown in Figure 13.
Figure 10. Experimental hardware setup.
Figure 11. Dead time measurement by Yokogawa precision power analyser.
Figure 12. Experimental results of the line-line voltage and line current with Ma = 0.8 for HSVPWM.
Figure 13. Comparison of simulation results with experimental results of voltage harmonic spectrum for Ma = 0.8 (harmonic order from 0 to 500).
8. Conclusion
In this paper, a hybrid Space Vector PWM switching patterns for three phase voltage source inverter is proposed. The main idea of the proposed PWM strategy is to combine the merits of both the SVPWM and RPWM. The HSVPWM is compared systematically with its counterparts SVPWM and RPWM. The results evidenced the success of the HSVPWM methods in term of improved fundamental component, reduced THD and minimal HSF. The strategy finds it suitability with the modern ac drives for noise free working. In addition, this method, blended successfully with FPGA, occupies less area and achieves low propagation delay with very less power dissipation. In future, more randomization can be performed by using 16 bit or 32 bit LFSRs.
Cite this paper
P. Muthukumar,P. Melba Mary,S. Jeevananthan,1 1, (2016) An Improved Hybrid Space Vector PWM Technique for IM Drives. Circuits and Systems,07,2120-2131. doi: 10.4236/cs.2016.79184
References
- 1. Bose, B.K. (2002) Modern Power Electronics and AC Drives. Prentice-Hall PTR, Upper Saddle River, 210-224.
- 2. Hmidet, A., Dhifaoui, R. and Hasnaoui, O. (2010) Development, Implementation and Experimentation on a DSPACE DS1104 of a Direct Voltage Control Scheme. Journal of Power Electronics, 10, 468-476.
http://dx.doi.org/10.6113/JPE.2010.10.5.468 - 3. Ursaru, O., Aghion, C., Lucanu, M. and Tigaeru, L. (2009) Pulse Width Modulation Command Systems Used for the Optimization of Three Phase Inverters. Advances in Electrical and Computer Engineering, 9, 22-27.
http://dx.doi.org/10.4316/aece.2009.01004 - 4. Trzynadlowski, A.M., Bech, M.M., Blaabjerg, F. and Pedersen, J.K. (1999) An Integral Space-Vector PWM Technique for DSP-Controlled Voltage-Source Inverters. IEEE Transactions on Industry Applications, 35, 1091-1097.
http://dx.doi.org/10.1109/28.793370 - 5. Ohnuma, Y. and Itoh, J.I. (2010) Space Vector Modulation for a Single Phase to Three Phase Converter Using an Active Buffer. International Power Electronics Conference, Sapporo, 21-24 June 2010, 574-580.
http://dx.doi.org/10.1109/ipec.2010.5543304 - 6. Hariram, B. and Marimuthu, N.S. (2005) Space Vector Switching Patterns for Different Applications—A Comparative Analysis. IEEE International Conference on Industrial Technology, Hong Kong, 14-17 December 2005, 1444-1449.
http://dx.doi.org/10.1109/icit.2005.1600862 - 7. Boopathi, R., Muthukumar, P., Melbamary, P. and Jeevananthan, S. (2012) Investigations on Harmonic Spreading Effects of SVPWM Switching Patterns in VSI Fed AC Drives. IEEE International Conference on Advances in Engineering, Science and Management, Nagapattinam, 30-31 March 2012, 651-656.
- 8. Soumitra, D.A.S. and Narayanan, G. (2012) Noval Switching Sequences for a Space-Vector-Modulated Three-Level Inverter. IEEE Transactions on Industrial Electronics, 59, 1477-1487.
http://dx.doi.org/10.1109/TIE.2011.2163373 - 9. Krishnakumar, C., Muhilan, P., Sathiskumar, M. and Sakthivel, M. (2015) A New Random PWM Technique for Conducted-EMI Mitigation on Cuk Converter. Journal of Electrical Engineering & Technology, 10, 916-924.
http://dx.doi.org/10.5370/JEET.2015.10.3.916 - 10. Kim, K.-S., Jung, Y.-G. and Lim, Y.-C. (2009) A New Hybrid Random PWM Scheme. IEEE Transactions on Power Electronics, 24, 192-200.
http://dx.doi.org/10.1109/TPEL.2008.2006613 - 11. Lim, Y.-C., Wi, S.-O., Kim, J.-N. and Jung, Y.-G. (2010) A Pseudo Random Carrier Modulation Scheme. IEEE Transactions on Power Electronics, 25, 797-805.
http://dx.doi.org/10.1109/TPEL.2009.2035699 - 12. Wang, Z., Chau, K.T. and Cheng, M. (2008) A Chaotic PWM Motor Drive for Electric Propulsion. IEEE Vehicle Power and Propulsion Conference, Harbin, September 2008, 1-6.
- 13. Sutikno, T., Jidin, A. and Idris, N.R.N. (2010) New Approach FPGA-Based Implementation of Discontinuous SVPWM. Turkish Journal of Electrical Engineering and Computer Sciences, 18, 499-514.
- 14. Akin, O. and Alan, I. (2010) The Use of FPGA in Field-Oriented Control of an Induction Machine. Turkish Journal of Electrical Engineering and Computer Sciences, 18, 943-962.















