Circuits and Systems
Vol.07 No.05(2016), Article ID:66166,12 pages
10.4236/cs.2016.75048
Optimization of Thermal Aware VLSI Non-Slicing Floorplanning Using Hybrid Particle Swarm Optimization Algorithm-Harmony Search Algorithm
Sivaranjani Paramasivam1, Senthilkumar Athappan2, Eswari Devi Natrajan1, Maheswaran Shanmugam1
1Department of Electronics and Communication Engineering, Kongu Engineering College, Erode, India
2Department of Electrical and Electronics Engineering, Dr. Mahalingam College of Engineering and Technology, Pollachi, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 February 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
Floorplanning is a prominent area in the Very Large-Scale Integrated (VLSI) circuit design automa- tion, because it influences the performance, size, yield and reliability of the VLSI chips. It is the process of estimating the positions and shapes of the modules. A high packing density, small fea- ture size and high clock frequency make the Integrated Circuit (IC) to dissipate large amount of heat. So, in this paper, a methodology is presented to distribute the temperature of the module on the layout while simultaneously optimizing the total area and wirelength by using a hybrid Particle Swarm Optimization-Harmony Search (HPSOHS) algorithm. This hybrid algorithm employs diversification technique (PSO) to obtain global optima and intensification strategy (HS) to achieve the best solution at the local level and Modified Corner List algorithm (MCL) for floorplan representation. A thermal modelling tool called hotspot tool is integrated with the proposed algorithm to obtain the temperature at the block level. The proposed algorithm is illustrated using Microelectronics Centre of North Carolina (MCNC) benchmark circuits. The results obtained are compared with the solutions derived from other stochastic algorithms and the proposed algorithm provides better solution.
Keywords:
VLSI Non-Slicing Floorplan, Modified Corner List (MCL) Algorithm, Hybrid Particle Swarm Optimization-Harmony Search Algorithm (HPSOHS)

1. Introduction
VLSI physical design automation process plays an important role in fabrication of ICs. In the physical design cycle, floorplanning is a significant step because it affects the successive process such as placement and routing. It is the process of arranging the modules in the layout such that each module has their fixed position in the layout and no modules overlap with each other. To handle the design complexity, Intellectual Property (IP) modules are widely used. This makes the floorplanning problem as Non-Deterministic Polynomial time (NP) hard problem. From literature [1] , metaheuristic algorithms are applied to handle NP-hard problem more efficiently. Floorplan is of two forms: 1) slicing floorplan, 2) non-slicing floorplan. In non-slicing floorplan, modules in the layout cannot be obtained by either horizontal or vertical bisection. Area occupied by slicing floorplan representation [2] [3] is large compared to non-slicing representation. Also, modules in the floorplan can be either hard modules or soft modules. Hard modules have fixed width (W) and height (H) whereas soft modules have varied aspect ratio. So, most of the research focuses on improving the performance of VLSI floorplanning using non-slicing representation with soft modules [4] - [7] .
To represent non-slicing floorplan, different representations are proposed: tree-based approach [5] sequence based approach [4] [8] , corner list approach [6] [9] and transitive closure graph [10] . From the literature, corner list method shows better representation in terms of search space O((n!)2) and computational complexity O(n). Since VLSI floorplanning is an NP-hard problem, different stochastic algorithms [11] - [17] are proposed to optimize non-slicing floorplan. Normally, simulated annealing (SA) technique [8] [11] [14] - [16] is widely applied in VLSI layout. SA algorithm gives competitive results for small number of modules. As the number of module increases, it takes significant computational resources. So, at recent times thrust is given to population based algorithm.
PSO based approach for VLSI floorplanning is proposed, exhibits rapid convergence, leads to more optimal solutions and gives reasonable solutions only on the hard IP modules placement problem. Memetic Algorithm (MA) [18] for a non-slicing VLSI floorplanning problem is proposed. It uses an effective genetic search method to explore the search space and an efficient local search method to exploit information in the search region. Solutions obtained by MA have smaller area but longer interconnection. Harmony search algorithms, genetic algorithm, and artificial bee colony algorithm are proposed for VLSI non-slicing floorplan representation. These algorithms have either diversification or intensification capability. So, a good optimization algorithm shall have a balance between both exploration and exploitation capability. VLSI floorplanning algorithms emphasizing both exploration and exploitation are rarely found in the literature.
Hybridization of PSO and GA [19] with B*-tree for VLSI floorplan is carried out and works well for single objective floorplanning problem. Limitations in the above work are as follows: GA gets trapped into local minima and has more parameters to be tuned; the initial representation using B*-tree may change after packing process and adjacency information is incomplete. The above problems can be eliminated by incorporating a suitable heuristic algorithm and the data structure representing floorplan representation can also be modified. Different literature [20] [21] on harmony search algorithm shows the capability of escaping from local optima.
High packing density of the transistor with miniaturization in size leads to an increase in power density of the chip. As the power density of the chip increases, heat dissipation also increases, which is also an important metric to be considered for floorplanning problem. Different methods have been proposed to handle thermal aware VLSI floorplanning. Most of the research confined to optimizing area and temperature. So, research pertaining to exploiting the features of PSO and HS algorithm for floorplanning to optimize area, wire length and temperature is rarely found in the literature. Hotspot, a fast thermal modelling tool [22] is developed to handle VLSI floorplanning at block level.
Hence, hybridizing these two algorithms that are individually good at exploration (PSO) [23] and exploitation (HS) respectively will lead to a balanced algorithm. Mostly, performance of the floorplanning algorithm is evaluated based on the metric area and wirelength. A new methodology which integrates: MCL algorithm for floorplan representation (with search space O((n!)2 and computational complexity O(n)), PSO and HS algorithm (for their best global and local search mechanism) for soft modules, hotspot tool (for thermal modelling) is proposed in this paper.
The paper is structured as follows. Section 2 provides the problem statement. Section 3 depicts the proposed methodology. Section 4 illustrates the application of MCL algorithm, PSO-HS algorithm and hotspot tool for thermal aware VLSI floorplanning. Section 5 provides the results. Finally, Section 6 concludes the paper.
2. Problem Statement
Let there are “N” number of modules in the floorplan given as 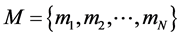 respectively. Each module
respectively. Each module 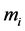 is characterized by two values: width of the module,
is characterized by two values: width of the module, 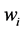 and height of the module,
and height of the module, 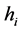 where,
where,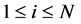 .
.
The objective of the floorplanning is to place the module without overlap in the layout and to optimize the cost metric such as area, wirelength and temperature with the following constraints:
1) Modules lies parallel to their x and y-coordinates.
2) No two modules overlap with each other.
3) Satisfying the Shape functions of floorplanning.
The fitness function of the proposed work is given as
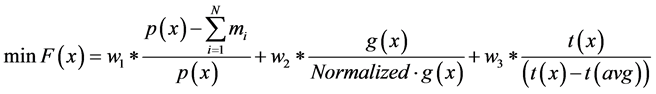 (1)
(1)
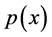 is the x’s floorplan area.
is the x’s floorplan area.
 is the sum of area of the modules.
is the sum of area of the modules.
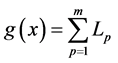 is obtained wirelength.
is obtained wirelength.
 = half perimeter wirelength of m net.
= half perimeter wirelength of m net.
Normalized 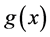 is average wirelength of 1000 iterations.
is average wirelength of 1000 iterations.
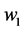 ,
, 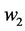 &
& 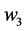 are constant weight values ranging between 0 to 1.
are constant weight values ranging between 0 to 1.
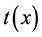 is maximum temperature in the chip.
is maximum temperature in the chip.

Weighted sum technique is used to merge multiobjective function into a scalar objective function. Each objective in the fitness function is calculated in different units (area―mm2, wirelength―mm & temperature―˚C). So to get a linear objective function, each term in the fitness function is normalized. According to designer’s specification and priority, values are assigned to the weights in the fitness function.
3. Proposed HPSOHS Algorithm
The process of hybridizing PSO and HS algorithm to optimize the floorplan fitness function is proposed in the following steps:
Step 1: Load the modules and initialize the parameters of the PSO algorithm.
Step 2: Generate an initial population with particle dimension corresponding to the number of modules to be optimized and initialize its positions.
Step 3: Calculate the fitness value of each particle using MCL placement strategy (area) and HPWL (wirelength) and then assign the fitness values to its corresponding particles. Let the initial global best be the lowest Pbest value.
Step 4: Update the velocity of the particle.
Step 5: In the consecutive iterations check every particle. If its fitness value is better than its corresponding previous Pbest, then update its Pbest along with the fitness value and particle.
Step 6: Update Gbest for each and every iteration. If the earlier Gbest is higher than the Gbest obtained in current iteration, then update newer one as the final Gbest.
Step 7: Repeat step 3 to step 6 till the termination condition is reached. The termination condition or stopping criteria may be the end of number of iteration or the repetitive occurrence of the same output for certain number of iterations specified by the user.
Step 8: If termination condition is satisfied, then pass on the Pbest particle as the input harmonies to the HS algorithm.
Step 9: Initialize the Pbest particles obtained from the PSO as initial harmonies of the HS algorithm.
Step 10: Evaluate the fitness value of the harmonies and update the harmonies in HM.
Step 12: Repeat the process, till the termination condition is reached.
4. Algorithm Representation
4.1. Modified Corner List Representation
CL is a sequence-based representation used to represent the initial floorplan [9] . In MCL based approach, the floorplan layouts can be formed using corner list. The property of MCL is: If there are n numbers of modules to be placed onto the floorplan region then, (n + 1) possible number of corners exists, if and only if width of all modules is not same. If two modules are of equal size, then it is considered as a single module.
The description of the above steps and MCL placement strategy is shown in Figure 1. Red coloured dots denote the corners that are formed due to the placement of modules on the floorplan region. In order to place the next block available into the floorplan region a corner is selected in random manner denoted by Grey coloured dots. In Figure 1(a) two red corners are formed due to the placement of module “1”. Among these two corners (grey coloured) shown in Figure 1(b) one corner is selected in random manner for the placement of module “2”. The placement of module “2” further leads to the creation of two more red corners as shown in Figure 1(c). In Figure 1(c), the top corner generated due to module “2” is not considered as per MCL property. By above process the creation of dead space between module “3” and module “4” is eliminated in following steps of placement of remaining modules as shown in Figures 1(d)-(f).
4.2. Particle Swarm Optimization
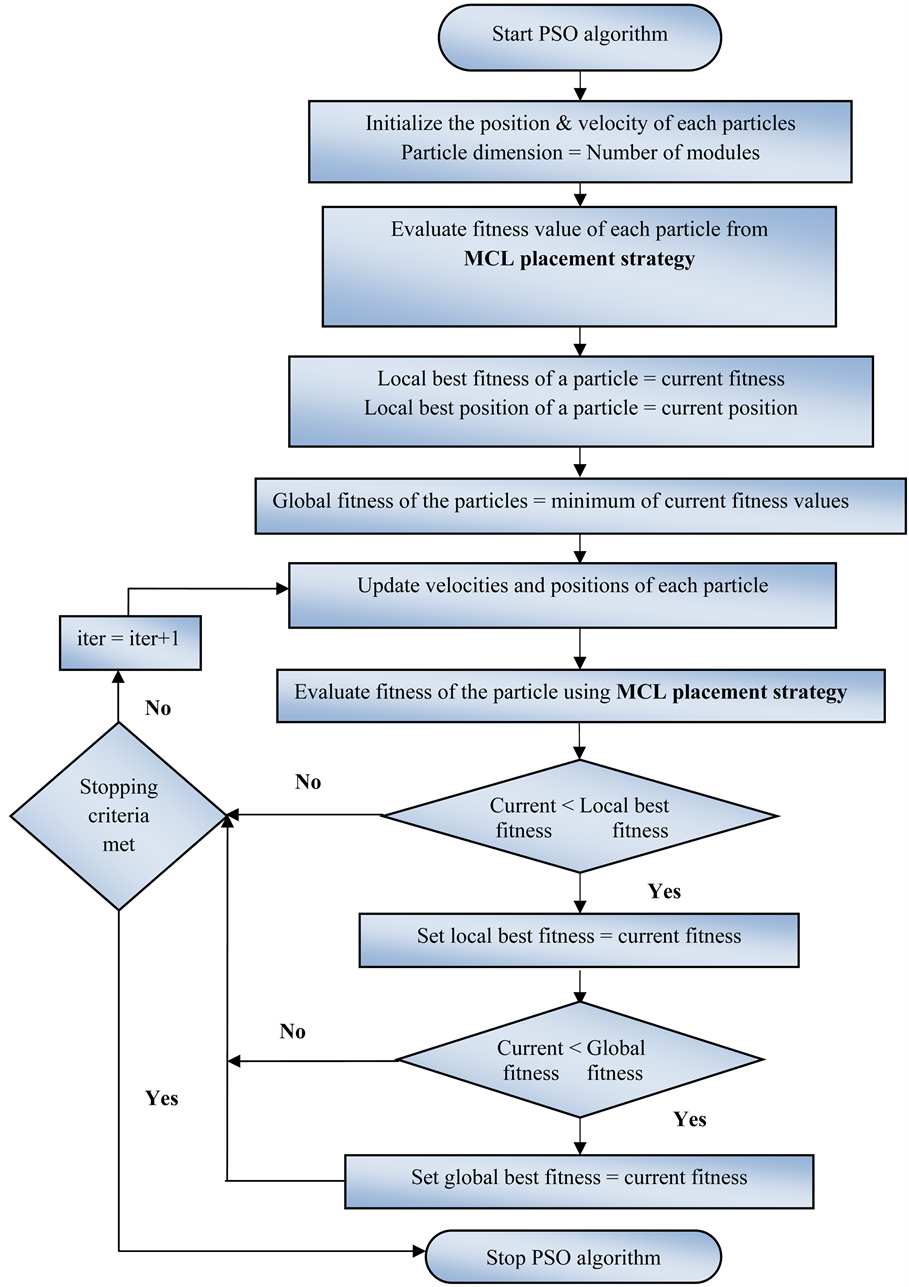
PSO is a bio-inspired algorithm based on population [24] [25] . The algorithm starts after defining the population of candidate solutions. The individual elements of the population are known as particles. For individual particles the fitness value is calculated. Detailed flowchart of the proposed PSO algorithm is shown in Figure 2.
The position of each and every particle is updated for all iteration by using a velocity term that is defined by the following Equation (2) and Equation (3):


where, Vid denotes velocity of the particle, Xid denotes current position of the particle, c1 & c2 is used to determine the relative influence of the cognitive and social components, rand() denotes random number generated between 0 and 1, Pid denotes Personal best (pbest) of the particle i, Pgd represents Global best (gbest) of the group, t denotes iteration index, d denotes number of dimensions (variables), w denotes inertia weight.
Figure 1. (a)-(f) packing process of MCL strategy.
Figure 2. Flowchart of PSO algorithm.
4.3. Harmony Search Algorithm
HS algorithm [21] is a meta-heuristic and derivative-free algorithm based on music improvisation which is inspired by harmony present in the music. Harmony Memory Size (HMS), Harmony Memory Consideration Rate (HMCR) and Pitch Adjustment Rate (PAR) are the control parameters of HS algorithm. New harmony



explained above. The HMCR value varies between 0 and 1; it is rate of selecting a particular value from the already stored values in HM, whereas (1-HMCR) is the rate of choosing a fresh value (random value) within the available possible limit (

Every solution vector obtained is further considered in order to determine whether it should be adjusted based on its pitch value. Pitch adjustment is done using the PAR parameter. It controls the amount of pitch to be adjusted as shown in Equation (5).
Figure 3. Flowchart of harmony search algorithm.

where, BW represents an arbitrary bandwidth and rand( ) is a random number generated between 0 and 1.
4.4. Interfacing of HPSOHS and Hotspot Tool
For calculation of temperature several models of hotspot are available. In this work, due to simplicity and high speed, block model (base model) is used. This trace level simulator takes floorplan file (.flp) and power trace file (ptrace) as inputs and the output is the corresponding transient temperature of each individual module (Ttrace). The tool considers ptrace and .flp file (generated by HPSOHS) as arguments and produces the corresponding peak temperature of the respective floorplan. Interfacing of hotspot tool and the proposed algorithm is shown in Figure 4.
As shown in the Figure 4, for each and every iteration in HPSOHS, hotspot gets invoked. For every new solution, multi-objective such as area, wirelength and peak temperature (from hotspot tool) are calculated. Based on this, multi-objective optimization process is carried out to produce nearer-optimal floorplan which is thermally balanced. The proposed floorplanner takes inputs in terms of block/net files for MCNC benchmark circuits and generates output as floorplan (.flp file). ptrace file and configuration file are given to hotspot tool along with .flp file. As mentioned in the literature [12] , ptrace file is file which has power values from 0.05 mW to 3 W which are randomly assigned to each modules in the floorplan.
5. Results and Discussion
5.1. Solution Encoding for PSO & HS
In hybrid PSO-HS algorithm, each particle and harmonies corresponds to a potential solution. Table 1 shows the initialization of particles/harmony. Feasible solutions can be decoded to obtain layout of the floorplan. Each par- ticle/harmonies represents the order in which the modules are to be placed in the floorplan using MCL represen- tation. The number of values in each particle/harmony will be exactly same as that of total modules to be placed.
Figure 4. Interfacing of hotspot tool with HPSOHS algorithm.
Each particle/harmony is assigned a random number and concatenates it with module number. After initializa- tion of particle/harmony, sort the columns of each particle/harmony either in ascending or descending order. By this method, modules of each particle/harmony are reordered and a new sequence of module will be generated for each and every particle/harmony. Based on the new order of module, by using MCL representation the floor- plan is generated. Next, evaluate the fitness value of each particle/harmony from MCL representation for the respective sequence of modules.
5.2. Performance of the Proposed Algorithm
The performance of HPSOHS algorithm for VLSI non-slicing floorplanning is analyzed and compared with existing algorithms (reported in the literature). The results are shown in the following sections. By empirical analysis, parameter setting for PSO and HS algorithm is shown in Table 2.
To evaluate the effectiveness of HPSOHS algorithm, standard MCNC benchmark circuits are considered and compared with the existing algorithms reported in the literature. Characteristics of MCNC Benchmark Circuits are shown in Table 3. Different performance measures are considered like area, wirelength and dead space obtained on the MCNC benchmarks are compared with standard stochastic and heuristics algorithms reported in the literature.
Different weight values have been assigned to the weight factor in the objective function and simulations are being carried out based on both single objective and multi-objective optimization. Tables 4-6 compare the performance of the proposed HPSOHS with that of other algorithm [26] - [28] for MCNC benchmark circuits with different weight values.
Table 1. Initialization of particles/harmony.
Table 2. Parameter setting for HPSOHS algorithm.
Table 3. Characteristics of MCNC benchmark circuits.
Table 4. Comparison of results on MCNC benchmark circuits with 

Table 5. Comparison of results of MCNC benchmark circuits with 

Table 6. Comparison of thermal aware floorplan for different algorithms.
The results obtained are compared with the solutions derived from other stochastic algorithms. The MCL based algorithm explores the search space and the HPSOHS algorithm balances global exploration and local exploitation. Reduction of dead space with HPSOHS and SA algorithm and amount of improvements are: apte: 2.52%, xerox: 4.21%, hp: 10.79%, ami33: 9.73% and ami49: 6.66%. There is a considerable reduction in dead space (PSO vs HPSOHS) and amount of improvement for MCNC benchmarks are: hp: 2.56%, ami33: 7.65% and ami49: 11.42%. Performance of the algorithm is also analyzed using (Gigascale Systems Research Centre) GSRC circuits. Simulation result of GSRCn100 using HPSOHS is shown in Figure 5. Total number of module for GSRCn100 is 100, after simulation the effective floor plan area for n100 circuit is 17.9501 mm2 and the dead space (unused space) in the floor plan is only 0.122%. Simulation result shows that the proposed algorithm woks better for larger number of modules.
The hotspot simulation result of MCNC apte with 9 modules and total area occupied by modules is 47.4 mm2 and dead space as 6.294% is shown in Figure 6. It is observed that the hottest module 4 can be placed near colder module/low power density module (5 and 9) so that there is a heat diffusion to the colder module and dead space region, which in turn reduces the temperature of module 4.
Figure 5. Simulation result of thermal balanced floorplan for ami33 circuit.
Figure 6. Simulation result of thermal balanced floorplan for apte circuit.
6. Conclusion
HS is a divergence free algorithm and has the advantage of escaping from local optima. Hence, hybridization of HS with PSO handles the problem of balancing global exploration and local exploitation. The simulation results for MCNC benchmark circuit demonstrate that the proposed algorithm achieves the optimal solution especially for larger number of modules. HPSOHS for a thermal aware floor planning by employing the thermal framework hotspot tool is implemented. There is a considerable reduction in peak temperatures of circuits in MCNC benchmarks for floor planning applications with minimal increase in area and wire length when compared to previous research. The data structure of hotspot tool is modified, so that it accepts the output from HPSOHS and returns temperature of each block which is considered as one of the parameters in the fitness function. On the other hand, the penalty in increase in area is only 2% as compared to HPSOHS


Cite this paper
Sivaranjani Paramasivam,Senthilkumar Athappan,Eswari Devi Natrajan,Maheswaran Shanmugam, (2016) Optimization of Thermal Aware VLSI Non-Slicing Floorplanning Using Hybrid Particle Swarm Optimization Algorithm-Harmony Search Algorithm. Circuits and Systems,07,562-573. doi: 10.4236/cs.2016.75048
References
- 1. Grosan, C. and Abraham, A. (2007) Hybrid Evolutionary Algorithms: Methodologies, Architectures, and Reviews. Studies in Computational Intelligence, 75, 1-17.
http://dx.doi.org/10.1007/978-3-540-73297-6_1 - 2. Deineko, V.G. and Woeginger, G.J. (2003) Complexity and Approximability Results for Slicing Floorplan Designs. European Journal of Operational Research, 149, 533-539.
http://dx.doi.org/10.1016/S0377-2217(02)00527-1 - 3. Valenzuela, C.L. and Wang, P.Y. (2002) VLSI Placement and Area Optimization Using a Genetic Algorithm to Breed Normalized Postfix Expression. IEEE Transaction on Evolutionary Computation, 6, 390-401.
http://dx.doi.org/10.1109/TEVC.2002.802872 - 4. Nakatake, S., Fujiyoshi, K., Murata, H. and Kajitani, Y. (1996) Module Placement on BSG Structure and IC Layout Application. Proceedings of IEEE/ACM International Conference on Computer-Aided Design, 484-491.
http://dx.doi.org/10.1109/ICCAD.1996.569870 - 5. Guo, P.N., Cheng, C.K. and Yoshimura, T. (1999) An O-Tree Representation of Non-Slicing Floor Plans and Its Applications. Proceedings of 36th annual ACM/IEEE Conference on Design Automation, 1 June 1999, 268-273.
- 6. Hong, X., Huang, G., Cai, Y., Gu, J., Dong, S., Cheng, C.K. and Gu, J. (2000) Corner Block List: An Effective and Efficient Topological Representation of Nonslicing Floorplan. Proceedings of IEEE/ACM International Conference on Computer-Aided Design, 5 November 2000, 8-12.
- 7. Nakatake, S., Furuya, M. and Kajitani, Y. (1998) Module Placement on BSG-Structure with Preplaced Modules and Rectilinear Modules. Proceedings of Asia and South Pacific—Design Automation Conference, 10 February 1998, 571- 576.
- 8. Murata, H., Fujiyoshi, K., Nakatake, S. and Kajitani, Y. (1996) VLSI Module Placement Based on Rectangle-Packing by the Sequence Pair. IEEE Transactions on Computer Aided Design of Integrated Circuits and System, 15, 1518- 1524.
http://dx.doi.org/10.1109/43.552084 - 9. Hoo, C.S., Jeevan, K., Ganapathy, V. and Ramiah, H. (2013) Variable-Order Ant System for VLSI Multi Objective Floor Planning. European Journal of Applied Soft Computing, 13, 3285-3297.
http://dx.doi.org/10.1016/j.asoc.2013.02.011 - 10. Lin, J.M. and Chang, Y.W. (2005) TCG: A Transitive Closure Graph Based Representation for General Floorplans. IEEE Transactions on Very Large Scale Integration Systems, 13, 288-292.
http://dx.doi.org/10.1109/TVLSI.2004.840760 - 11. Han, Y. and Koren, I. (2007) Simulated Annealing Based Temperature Aware Floorplanning. Journal of Low Power Electronics, 3, 141-155.
http://dx.doi.org/10.1166/jolpe.2007.128 - 12. Hung, W.L., Xie, Y., Vijaykrishnan, N., Addo-Quaye, C., Theocharides, T. and Irwin, M.J. (2005) Thermal-Aware Floorplanning Using Genetic Algorithms. Proceedings of 6th International Symposium on IEEE Quality of Electronic Design, 21 March 2005, 634-639.
http://dx.doi.org/10.1109/ISQED.2005.122 - 13. Lin, C.T., Chen, D.S. and Wang, Y.W. (2006) Modern Floorplanning with Boundary and Fixed-Outline Constraints via Genetic Clustering Algorithm. Journal of Circuits, Systems, and Computers, 15, 107-127.
http://dx.doi.org/10.1142/S0218126606002940 - 14. Wang, L. (2014) Fast Algorithms for Thermal-Aware Floorplanning. Journal of Circuits, Systems, and Computers, 23, Article ID: 1450098.
http://dx.doi.org/10.1142/s0218126614500984 - 15. Chen, J., Zhu, W. and Ali, M. (2011) A Hybrid Simulated Annealing Algorithm for Nonslicing VLSI Floorplanning. Systems, Man, and Cybernetics, 41, 544-553.
http://dx.doi.org/10.1109/TSMCC.2010.2066560 - 16. Anand, S., Saravanasankar, S. and Subbaraj, P. (2012) Customized Simulated Annealing Based Decision Algorithms for Combinatorial Optimization in VLSI Floorplanning Problem. Computational Optimization and Applications, 52, 667-689.
http://dx.doi.org/10.1007/s10589-011-9442-y - 17. Chen, G., Guo, W. and Chen, Y. (2010) A PSO-Based Intelligent Decision Algorithm for VLSI Floorplanning. Soft Computing, 14, 1329-1337.
http://dx.doi.org/10.1007/s00500-009-0501-6 - 18. Tang, M. and Yao, X. (2007) A Memetic Algorithm for VLSI Floorplanning. IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, 37, 62-69.
http://dx.doi.org/10.1109/TSMCB.2006.883268 - 19. Sivaranjani, P. and Senthilkumar, A. (2015) Thermal-Aware Non-Slicing VLSI Floorplanning Using a Smart Decision- Making PSO-GA Based Hybrid Algorithm. Journal of Circuits, Systems, and Signal Processing, 34, 3521-3542.
http://dx.doi.org/10.1007/s00034-015-0020-x - 20. Yang, X.S. (2009) Harmony Search as a Metaheuristic Algorithm. In: Music-Inspired Harmony Search Algorithm, Springer Berlin Heidelberg, 1-14.
http://dx.doi.org/10.1007/978-3-642-00185-7_1 - 21. Geem, Z.W., Kim, J.H. and Loganathan, G.V. (2001) A New Heuristic Optimization Algorithm: Harmony Search. Simulation, 76, 60-68.
http://dx.doi.org/10.1177/003754970107600201 - 22. HotSpot-HOW TO (2010)
http://lava.cs.virginia.edu/HotSpot/.html - 23. Kennedy, J. (2010) Particle Swarm Optimization, Encyclopedia of Machine Learning. Springer, US, 760-766.
- 24. Tarique, A. and Gabber, H.A. (2013) Particle Swarm Optimization (PSO) Based Turbine Control. Intelligent Control and Automation, 4, 126-137.
http://dx.doi.org/10.4236/ica.2013.42018 - 25. Zhang, C., Ding, Y., Wu, Q., Wang, Q. and Ostergaard, J. (2013) Distribution Network Expansion Planning Based on Multi-Objective PSO Algorithm. Energy and Power Engineering, 5, 975-979.
http://dx.doi.org/10.4236/epe.2013.54B187 - 26. Hung, W.L., Xie, Y., Vijaykrishnan, N., Addo-Quaye, C., Theocharides, T. and Irwin, M.J. (2005) Thermal-Aware Floorplanning Using Genetic Algorithms. IEEE Sixth International Symposium on Quality of Electronic Design, 634- 639.
http://dx.doi.org/10.1109/ISQED.2005.122 - 27. Xu, N. (2006) Floorplanning for Even On-Chip Thermal Distribution. Proceedings of International Conference on Communications, Circuits and Systems, 4, 2411-2414.
http://dx.doi.org/10.1109/ICCCAS.2006.285163 - 28. Qi, L.X., Xia, Y.S. and Wang, L. (2011) Simulated Annealing Based Thermal-Aware Floorplanning. Proceedings of International Conference on Electronics, Communications and Control, Ningbo, 9-11 September 2011, 463-466.
http://dx.doi.org/10.1109/icecc.2011.6067654