Circuits and Systems
Vol.06 No.05(2015), Article ID:56536,8 pages
10.4236/cs.2015.65015
Accurate Extraction of Effective Gate Resistance in RF MOSFET
Ikkyun Jo, Toshimasa Matsuoka
Graduate School of Engineering, Osaka University, Osaka, Japan
Email: jo@si.eei.eng.osaka-u.ac.jp, matsuoka@eei.eng.osaka-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2015; accepted 19 May 2015; published 22 May 2015
ABSTRACT
This paper describes the gate electrode resistance of MOSFET and non-quasi-static (NQS) effect for RF operation. The vertical current paths between the silicide layer and poly-silicon are considered in the gate electrode. The vertical current paths are not effective in long-channel devices, but become more significant in short-channel devices. The gate resistance including vertical current paths can reproduce the practical RF characteristics well. By careful separation of the above gate electrode resistance and the NQS effect, the small-signal gate-source admittance can be analyzed with 130-nm CMOS process. Elmore constant (κ) of the NQS gate-source resistance is about five for long-channel devices, while it decreases down to about three for short-channel devices.
Keywords:
MOSFET, NQS Effect, Gate Electrode Resistance, Elmore Constant

1. Introduction
CMOS device technology realizing low-power, large-scale integration and low-cost to manufacture is recently matching demands for miniaturization, low-power operation in wireless communication systems [1] -[4] . Scaling CMOS devices also are overwhelming the performance, such as unity-current-gain cut-off frequency ft, against bipolar junction transistors and compound semiconductor devices, which are popular in RF circuits [5] . So, RF system on chip (SoC) integrating from digital domain to RF analog domain can be realized. Although complexity of such a RF SoC increases, its short development time is always forced. In such a situation, precise simulations of analog/RF circuits are important, and more accurate MOSFET model and analysis of parasitic elements are needed for their implementations [6] -[8] .
One of the important issues of the MOSFET model in RF operation is related to effective gate resistance which influences input impedance, maximum oscillation frequency fmax, and noise performance [9] -[11] . It is especially important in the design of multi-band and wide-band CMOS low-noise-amplifiers (LNAs) [12] -[15] . The RF input resistance in common-source MOSFET has two factors [8] [16] -[18] . The first is related to the physical gate electrode. The second originates from the channel itself in the intrinsic MOSFET region and its coupling with the gate-source capacitance Cgs, which causes a relaxation-time dependent phenomenon of channel charge response for a time-varying input signal, so called non-quasi-static (NQS) effect [19] [20] . The NQS gate-source resistance Rgsi of the MOSFET operating in saturation region is approximately given by
 (1)
(1)
where gm is the transconductance, and the Elmore constant κ is five for long-channel and is reported to be as small as one for short-channel devices [17] . Because the above two resistance factors have a different gate size dependence [18] , their separate analysis is important in scalable MOSFET model and is also useful in RF circuit design [8] . Therefore, the accurate resistance model of extrinsic gate electrode is required in advanced short- channel devices as well as the accurate prediction of κ. The accurate value of κ can be useful in some analytical design approaches of LNA [15] [21] .
In this paper, we present high-accuracy gate electrode resistance model. The model presented includes the vertical current paths between the silicide and poly-silicon layers in MOSFET. By careful separation of the gate electrode resistance and the NQS effect, the small signal gate-source admittance can be analyzed. From these values, the κ is derived.
This paper is organized as follows. Section 2 describes gate electrode resistances with vertical current paths. Section 3 presents a MOS equivalent circuit which includes extrinsic and intrinsic parameters, and mentions method of parameter extraction. In Section 4, some parameters extracted in 130-nm CMOS process as well as κ are verified and discussed. Finally, conclusions are drawn in Section 5.
2. Gate Electrode Resistance of MOSFET
The gate of conventional MOSFET model is composed of gate insulator, poly-silicon, silicide and metal. Figure 1(a) illustrates top-view and cross section of n-channel MOSFET with a gate length L and gate width W in the silicided poly-silicon gate technology. When feeding the signal to gate, it propagates in horizontal direction of the silicide on the gate electrode surface, and then in vertical direction of poly-silicon and gate insulator to effect channel. Gate electrode resistance of the MOSFET is composed of gate contact resistance between connecting the metal and silicide, resistance of the silicide itself, the interface resistance between the silicide and poly-silicon,

Figure 1. (a) Top-view and cross section of MOSFET (both-side gate connection) and (b) equivalent circuit of gate unit element.
and vertical resistance of the poly-silicon itself [22] . The interface resistance is important in the vertical signal propagation [11] , and its typical values are about 25 Ωμm2 (TiSi2) [11] and about 2 ~ 3 Ωμm2 (NiSi) [23] . In long-channel MOSFET, vertical current paths of the gate electrode are less effective than gate contact and silicide resistance. However, as gate length decreases, the influence of vertical current paths becomes more effective. As gate width decreases, the horizontal resistance decreases, while the vertical resistance increases inversely proportional to the gate width.
Each parts of gate electrode resistance can be expressed with lumped elements for the signal path length in a horizontal gate width direction dz using a transmission line model as illustrated in Figure 1(b), which is similar to that in silicided diffusion region [24] . Here, Rcg is unit gate contact resistance between the silicide and poly- silicon, ρsili is the sheet resistivity of the silicide, ρint is an interface resistivity between the silicide layer and poly-silicon, ρvp is the vertical resistivity of poly-silicon layer per unit dimension. Cox is unit capacitance of the gate insulator. For simplification in mathematical expression,  ,
, 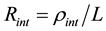 ,
, . When Cgc is defined as the capacitance between the gate and channel, we can consider it as
. When Cgc is defined as the capacitance between the gate and channel, we can consider it as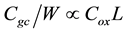 .
.
Considering the steady state at the angular frequency ω in Figure 1(b), the total admittance of vertical current path elements for unit signal propagation length on the gate electrode surface, Yvp, is given by
 (2)
(2)
From the manipulation described in Appendix, the gate electrode resistance seen from the gate contact position for unit gate finger with length Wf is expressed as
 (3)
(3)
where k is 1 and 1/4 for a single-side and a both-side gate connections, respectively.
Additionally, considering the gate contact between the silicide and metal as well as the gate extension to the channel area in a similar way based on the previous work [7] , the gate electrode resistance for the number of gate finger Nf is expressed as
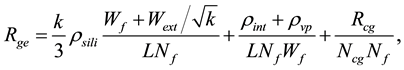 (4)
(4)
where Wext is the distance between the channel area edge and gate contact, and Ncg is the number of gate contacts per finger [7] . Capacitive coupling of the gate extension to the substrate is also considered in the above equation by using a factor 1/3. Compared to the previous works [7] [8] , Equation (4) has the second term inversely proportional to the channel area LNfWf, which originates from the vertical resistance elements. As the channel area decreases, this influence increases.
3. Parameter Extraction for NQS Resistances
In low-frequency operation, carriers in the channel can respond immediately to the applied terminal voltages, which correspond to charging and discharging of the gate-source capacitance Cgs. This is considered as quasi- static operation. On the other hand, as the operation frequency gets much higher, the channel resistance influences response time of the carriers, which is NQS operation. Although the transconductance, drain conductance and large-signal operation are influenced by the NQS effect, the influence of the small-signal gate-source admittance ygs is crucial in the multi-band and wide-band LNA designs. This paper focuses on the small-signal gate-source admittance.
To estimate the NQS effect, the careful parameter extraction for MOSFET model is required. Figure 2(a) shows the small-signal equivalent circuit which includes external parasitic elements. In this work, the body is connected to the source, resulting in no body effect. Rgsi and Rgdi in Figure 2(b) give NQS effect. Rge is a gate electrode resistance, Rde and Rse are series resistances of drain and source, and Cgse and Cdse are overlap capacitances between gate/source and drain/source. Extraction method separates extrinsic and intrinsic parameters from two-port parameters of the MOSFET. In the first step, the external resistances (Rge, Rde and Rse) and the external capacitances (Cgde, Cgse and Cdse) are de-embedded from the two-port parameters of the MOSFET, using the

Figure 2. (a) Small-signal equivalent circuit of MOSFET including external parasitic elements and (b) its intrinsic part.
de-embedding technique [8] . The estimation technique of the external resistances and capacitances are described later. In the second step, the equivalent circuit including only intrinsic parameters can be obtained.
To estimate the external parameters, the cold biasing (VGS = VDS = 0 V) is utilized. It is assumed that the intrinsic parameters except for drain-source conductance gds are not presented in cold bias. External parameters are nearly independent on VGS. Thus, the Z-parameters of the MOSFET in the cold biasing can be obtained as follows:
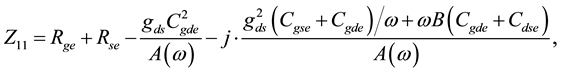 (5)
(5)
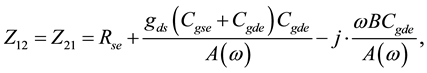 (6)
(6)
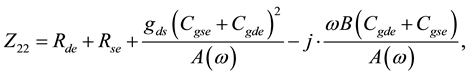 (7)
(7)
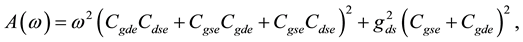

In the cold bias condition, gds is negligibly small. Assuming it, real parts of the Z-parameters in high frequency can be approximated as
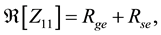 (8)
(8)


From these equations, Rge, Rde and Rse can be estimated. In addition, Using Equations (5)-(10) with the same assumption of small gds, imaginary parts of the Z-parameters can be approximated as.



From these equations, Cgse, Cgde and Cdse can be estimated.
The intrinsic Y-parameter matrix 




Based on the equivalent circuit shown in Figure 2(b), the parameters of MOSFET’s intrinsic parts can be calculated from relations of real and imaginary parts of Equation (16) as following equations.






4. Verification of Gate Electrode Model and NQS Effect
In this work, instead of on-chip high-frequency S-parameter measurement, simulated small-signal S-parameters are used with a RF MOSFET model (BSIM4 with GATEMOD = 3 [25] ), which can reproduce RF and DC characteristics well with many parameters for commercial 130-nm CMOS process. This can realize cost-effective verification of device models. As narrow gate width under 3 μm has an effect of the interface resistance on the gate resistance, NMOS devices with a single finger width of 3 μm and a both-side gate connection are used in this work. The embedded Z-parameter 
The external gate resistance Rge is extracted by using Equations (5)-(10), and is compared with calculated ones by using Equation (4). The results are illustrated in Figure 3. The second term of Equation (4) originates from the vertical current paths. To confirm the influence of the vertical current path in Figure 1, we calculated Rge with and without the second term (solid and dotted lines in Figure 3, respectively). The values of 
Based on the extracted external parameters, NQS gate-source resistance Rgsi and transconductance gm are extracted by using Equations (19) and (21). In this parameter extraction, to neglect high-order NQS effect [26] and delays in transconductance and drain conductance [8] , the maximum frequency is set to 6.5 GHz. Figure 4 shows the dependence of Rgsi on drain-source voltage VDS at the gate-source overdrive voltages 

Figure 5 shows Elmore constant κ obtained from extracted Rgsi and gm with Equation (1) as a function of gate length. As mentioned above, κ is around 5 for L > 1 μm. For L < 1 μm, it decreases to about 3, which may originate from velocity saturation [27] . The small-signal local channel conductance in the velocity saturation region
Figure 3. Extracted and calculated values of gate resistance Rge versus the number of gate figners Nf (L = 140 nm, Wf = 3 μm, both-side gate connection).

Figure 4. Extracted values of NQS gate-source resistance Rgsi of NMOS devices with gate length L = 140; 500; 1000; 2000 and 5000 nm at gate-source overdrive voltages (a) VGS − VTH = 0.4 V and (b) VGS − VTH = 0.8 V (gate width is 120 μm (3 μm × 40 fingers), both-side gate connection).
Figure 5. Gate length dependence of extracted Elmore constants κ.
is smaller than in the non-velocity-saturation source-side region. However, the value of κ around one, as reported in previous works [8] [17] , could not be confirmed even for minimum gate length (L = 140 nm) in this work. We guess the κ for short-channel devices may have a dependence on channel-length modulation, drain- induced barrier lowering, and so on, which show significant and complicated dependence on device structure.
5. Conclusion
In this work, the gate electrode resistance of MOSFET and NQS effect are analyzed using 130-nm CMOS process. The vertical current paths between silicide layer and poly-silicon are considered in MOSFET. The vertical current paths are not effective in the devices with large channel area, but become more significant as the channel area decreases. The gate electrode resistance including vertical current paths can reproduce well the practical RF characteristics. With the scaling of CMOS technology, this effect is not considered till now in RF CMOS circuit designs, but it has a significant effect in the design of multi-band and wide-band CMOS LNAs. By careful separation of the above gate electrode resistance and the NQS effect, the intrinsic small-signal parameters were extracted. The high-accuracy analysis considering physical characteristic with the vertical elements is verified. Elmore constant of the NQS gate-source resistance (κ) about five was confirmed for the long-channel devices, while it decreases down to about three for the short-channel devices. The value of κ around one, reported in previous works, could not be confirmed even for minimum gate length in this work. The NQS effect in short-channel devices may have significant and complicated dependence on device structure. For further studies, the analyses on various processes with various device structures are more required for RF CMOS circuit designs.
Acknowledgements
This study is supported by the VLSI Design and Education Center (VDEC), University of Tokyo, in collaboration with Agilent Technologies Japan, Ltd., and Cadence Design Systems, Inc.
References
- Rofougaran, A., Chang, J.Y.-C., Rofougaran, M. and Abidi, A.A. (1996) A 1 GHz CMOS RF Front-End IC for a Direct-Conversion Wireless Receiver. IEEE Journal of Solid-State Circuits, 31, 880-889.
- Razavi, B. (1999) CMOS Technology Characterization for Analog and RF Design. IEEE Journal of Solid-State Circuits, 34, 268-276.
- Kadoyama, T., Suzuki, N., Sasho, N., Iizuka, H., Nagase, I., Usukubo, H. and Katakura, M. (2004) A Complete Single-Chip GPS Receiver with 1.6-V 24-mW Radio in 0.18-μm CMOS. IEEE Journal of Solid-State Circuits, 39, 562- 568.
- Kamata, T., Okui, K., Fukasawa, M., Matsuoka, T. and Taniguchi, K. (2011) Low-Power Zero-IF Full-Segment ISDB- T CMOS Tuner with Tenth-Order Baseband Filters. IEEE Transactions on Consumer Electronics, 57, 403-410.
- Huang, Q., Piazza, F., Orsatti, P. and Ohguro, T. (1998) The Impact of Scaling Down to Deep Submicron on CMOS RF Circuits. IEEE Journal of Solid-State Circuits, 33, 1023-1036. http://dx.doi.org/10.1109/4.701249
- Enz, C.C. and Cheng, Y. (2000) MOS Transistor Modeling for RF IC design. IEEE Journal of Solid-State Circuits, 35, 186-201.
- Itoh, N., Ohguro, T., Katoh, K., Kimijima, H., Ishizuka, S., Kojima, K. and Miyakawa, H. (2003) Scalable Parasitic Components Model of CMOS for RF Circuit Design. IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences, E38-A, 288-298.
- Kim, G., Murakami, B., Goto, M., Kihara, T., Nakamura, K., Shimizu, Y., Matsuoka, T. and Taniguchi, K. (2006) Small-Signal and Noise Model of Fully Depleted Silicon-on-Insulator Metal-Oxide-Semiconductor Devices for Low- Noise Amplifier. Japanese Journal of Applied Physics, 45, 6872-6877. http://dx.doi.org/10.1143/JJAP.45.6872
- Shaeffer, D.K. and Lee, T.H. (1997) A 1.5-V, 1.5-GHz CMOS Low Noise Amplifier. IEEE Journal of Solid-State Circuits, 32, 745-759.
- Shaeffer, D.K. and Lee, T.H. (2005) Corrections to “A 1.5-V, 1.5-GHz CMOS Low Noise Amplifier”. IEEE Journal of Solid-State Circuits, 40, 1397-1398.
- Litwin, A. (2001) Overlooked Interfacial Silicide-Polysilicon Gate Resistance in MOS Transistors. IEEE Transactions on Electron Devices, 48, 2179-2181. http://dx.doi.org/10.1109/16.944214
- Utsurogi, Y., Haruoka, M., Matsuoka, T. and Taniguchi, K. (2005) CMOS Front-End Circuits of Dual-Band GPS Receiver. IEICE Transactions on Electronics, E88-C, 1275-1279. http://dx.doi.org/10.1093/ietele/e88-c.6.1275
- Ko, J., Kim, J., Cho, S. and Lee, K. (2005) A 19-mW 2.6-mm2 L1/L2 Dual Band CMOS GPS Receiver. IEEE Journal of Solid-State Circuits, 40, 1414-1425. http://dx.doi.org/10.1109/JSSC.2005.847326
- Jo, I., Bae, J., Matsuoka, T. and Ebinuma, T. (2013) Design of Triple-Band CMOS GPS Receiver RF Front-End. IEICE Electronics Express, 10, 20130126.
- Kihara, T., Matsuoka, T. and Taniguchi, K. (2010) A Transformer Noise-Canceling Ultra-Wideband CMOS Low-Noi- se Amplifier. IEICE Transactions on Electronics, E93-C, 187-199. http://dx.doi.org/10.1587/transele.E93.C.187
- Razavi, B., Yan, R.H. and Lee, K.F. (1994) Impact of Distributed Gate Resistance on the Performance of MOS Devices. IEEE Transactions on Circuits and Systems I, 41, 750-754. http://dx.doi.org/10.1109/81.331530
- Abou-Allam, E. and Manku, T. (1999) An Improved Transmission-Line Model for MOS Transistors. IEEE Transactions on Circuits and Systems II, 46, 1380-1387. http://dx.doi.org/10.1109/82.803477
- Cheng, Y.H. and Matloubian, M. (2001) High Frequency Characterization of Gate Resistance in RF MOSFETs. IEEE Electron Device Letters, 22, 98-100. http://dx.doi.org/10.1109/55.902844
- Smedes, T. and Klaassen, F.M. (1995) An Analytical Model for the Non-Quasi-Static Small-Signal Behaviour of Submicron MOSFETs. Solid-State Electronics, 38, 121-130. http://dx.doi.org/10.1016/0038-1101(94)E0032-A
- Tsividis, Y. (1999) Operation and Modeling of the MOS Transistor. 2nd Edition, McGraw-Hill, New York.
- Kihara, T., Kim, G., Goto, M., Nakamura, K., Shimizu, Y., Matsuoka, T. and Taniguchi, K. (2007) Analytical Expression Based Design of a Low-Voltage FD-SOI CMOS Low-Noise Amplifier. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E90-A, 317-325. http://dx.doi.org/10.1093/ietfec/e90-a.2.317
- Dormieu, B., Scheer, P., Charbuillet, C., Jaouen, H. and Danneville, F. (2013) Revisited RF Compact Model of Gate Resistance Suitable for High-K/Metal Gate Technology. IEEE Transactions on Electron Devices, 60, 13-19. http://dx.doi.org/10.1109/TED.2012.2225146
- Sonehara, T., Hokazono, A., Akutsu, H., Sasaki, T., Uchida, H., Tomita, M., Kawanaka, S., Inaba, S. and Toyoshima, Y. (2011) Mechanism of Contact Resistance Reduction in Nickel Silicide Films by Pt Incorporation. IEEE Transactions on Electron Devices, 58, 3778-3786. http://dx.doi.org/10.1109/TED.2011.2166557
- Scott, D.B., Hunter, W.R. and Shichijo, H. (1982) A Transmission Line Model for Silicided Diffusions: Impact on the Performance of VLS Circuits. IEEE Transactions on Electron Devices, 29, 651-661. http://dx.doi.org/10.1109/T-ED.1982.20758
- Liu, W.D. and Hu, C.M. (2011) BSIM4 and MOSFET Modeling For IC Simulation. World Scientific Publishing, Singapore.
- Lee, H.-J. and Lee, S. (2013) Accurate Non-Quasi-Static Gate-Source Impedance Model of RF MOSFETs. Journal of Semiconductor Technology and Science, 13, 569-575. http://dx.doi.org/10.5573/JSTS.2013.13.6.569
- Sodini, C.G., Ko, P.-K. and Moll, J.L. (1984) The Effect of High Fields on MOS Device and Circuit Performance. IEEE Transactions on Electron Devices, 31, 1386-1393. http://dx.doi.org/10.1109/T-ED.1984.21721
Appendix
The lumped elements of MOSFET's horizontal and vertical gate resistance can be composed as like Figure 1(b). The steady state at the angular frequency ω in only the gate electrode on the channel (





Thus, the voltage 



where 

The boundary conditions to obtain V+ and V− in case of a single-side gate connection (





where k is 1 and 1/4 for a single-side and a both-side gate connections, respectively. The approximation is valid
for



