Circuits and Systems
Vol. 3 No. 2 (2012) , Article ID: 18535 , 7 pages DOI:10.4236/cs.2012.32019
A Hybrid GA-SQP Algorithm for Analog Circuits Sizing
The Lyon Institute of Nanotechnology (INL), University of Lyon, Lyon, France
Email: Firas.yengui@gmail.com
Received December 30, 2011; revised March 2, 2012; accepted March 10, 2012
Keywords: Genetic Algorithm; Sequential Quadratic Programming; Hybrid Optimization; Analog Circuits; Transimpedance Amplifier; Optical Driver
ABSTRACT
This study presents a hybrid algorithm obtained by combining a genetic algorithm (GA) with successive quadratic sequential programming (SQP), namely GA-SQP. GA is the main optimizer, whereas SQP is used to refine the results of GA, further improving the solution quality. The problem formulation is done in the framework named RUNE (fRamework for aUtomated aNalog dEsign), which targets solving nonlinear mono-objective and multi-objective optimization problems for analog circuits design. Two circuits are presented: a transimpedance amplifier (TIA) and an optical driver (Driver), which are both part of an Optical Network-on-Chip (ONoC). Furthermore, convergence characteristics and robustness of the proposed method have been explored through comparison with results obtained with SQP algorithm. The outcome is very encouraging and suggests that the hybrid proposed method is very efficient in solving analog design problems.
1. Introduction
Since their appearance, the EDA (Electronic Design Automation) tools have helped to minimize the cost of production of very large scale integration (VLSI) electronics. This improvement is achieved thanks to the reduction of development time and to the relationship between sizes of circuits on the one hand and the complexity of performed functions on the other hand. EDA tools allow designing automatically digital circuits from specifications of design masks. However, the development of these tools dedicated to analog circuits is perceived as a very difficult activity.
Analog components constitute an important part of integrated electronic systems. This importance is manifested in terms of elements and area in mixed-signal systems and also as a vital part in digital systems. The nature of analog circuits makes their design complex.
It does not consist only of topology and layout synthesis but also of component sizing. This sizing is an iterative process, which, for analog circuits, is often manual and strongly relies on the designer’s intuition and experience to succeed. In manual procedures, it is common that the designer varies only one parameter of the circuit while keeping all the others fixed until obtaining the desired solution. Optimizing the sizes of the analog components automatically is an important issue towards being able to rapidly design true high performance circuits.
The problem of sizing an analog circuit can, indeed, be formulated as an optimization problem. Evolutionary algorithms, as a general purpose optimization technique, have proven strong efficiency for solving complex optimization problems. In this family of evolutionary algorithms, we find the Genetic Algorithms (GA) [1-3]. It remains the most recognized and practiced form of Evolutionary Algorithms. These are stochastic optimization techniques that mimic Darwin’s principles of natural selection and survival of the fittest. The main strength of GA is its fast convergence. However, GA performs better in a global search than in a localized one. In the last period of the evolution and when reaching a near optimal solution, the convergence rate decreases considerably, the algorithm stops optimizing, and thus the achieved accuracy of algorithm becomes limited [4].
This work deals with optimal sizing of the analog electronic parts of an Optical Network-on-Chip (ONoC). We mention the example of a TransImpedance Amplifier (TIA) and that of an optical driver (Driver) to which we apply a hybrid optimization approach, namely GA-SQP. GA is the main optimizer, whereas SQP (Sequential Quadratic Programming) [5] is used to fine tune the results of GA. At first, GA searches the global optimum in the whole solution region in order to obtain a quasi-optimal solution. It provides means to explore efficiently the design space. Then the global optimal solution can be obtained by SQP. This SQP significantly increases the power of the GA in terms of solution quality and speed of convergence to the optimal. Therefore, we used a framework, named RUNE (fRamework for aUtomated aNalog dEsign), to optimize a TIA and an Optical Driver circuits.
The remainder of the paper is organized as follows: Section 2 gives an overview of the RUNE framework. In Section 3, we recall the working principles of genetic and SQP algorithms and propose our hybrid approach GASQP. In Section 4, two application examples are given. The first application is a mono-objective problem that deals with optimizing the sizing of an optical driver circuit to meet fixed specifications. The second application is a multiobjective problem with two conflicting objecttives of a TIA circuit. Optimization results for the TIA circuit with proposed hybrid algorithm are compared with results obtained with SQP algorithm. Finally, we give a conclusion in Section 5.
2. The Framework RUNE
2.1. Overview of RUNE
RUNE (fRamework for aUtomated aNalog dEsign) [6,7] is an Analog/Mixed-Signal (AMS) synthesis framework. As shown in Figure 1, the main inputs are the hierarchical description of the system and associated system level performances. From the user’s point of view, there are two main phases leading to the synthesis of an (Intellectual Property) IP block:
• Definition of AMS soft-IP, described in the Extended Markup Language (XML) format (directly into an XML file or through the graphical user interface, GUI). In this step, all information related to the system must be provided (hierarchy, models, variables, performances specifications, etc.).
• Configuration of the AMS firm-IP synthesis method. In this step, the user must define an optimization strategy, i.e. a numerical method or algorithm and the formulation of the problem according to the specifications.
In RUNE, different kinds of models describing the whole or part of the system at a given representational abstraction level can be entered. These models are stored in a database allowing each soft-IP to be used as part of a system. Also, in order to evaluate the performance of these domain-specific models, a simulation Application Programming Interface (API) has been developed in order to plug in several external simulators. In this way, the user can select the external simulators to use in the specification evaluation phase.
2.2. Optimization Process
The optimization process can be used at each abstraction level and for every structural (sub-)component. Three main steps are followed (Figure 2):
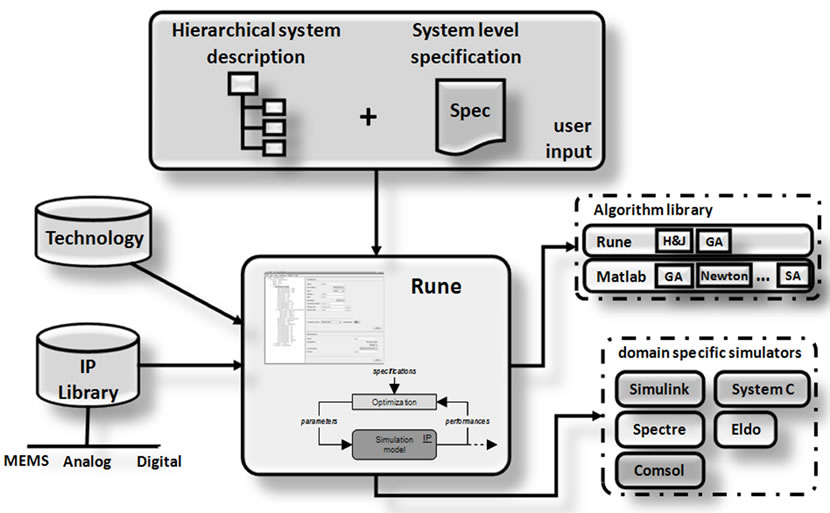
Figure 1. RUNE block diagram functions.
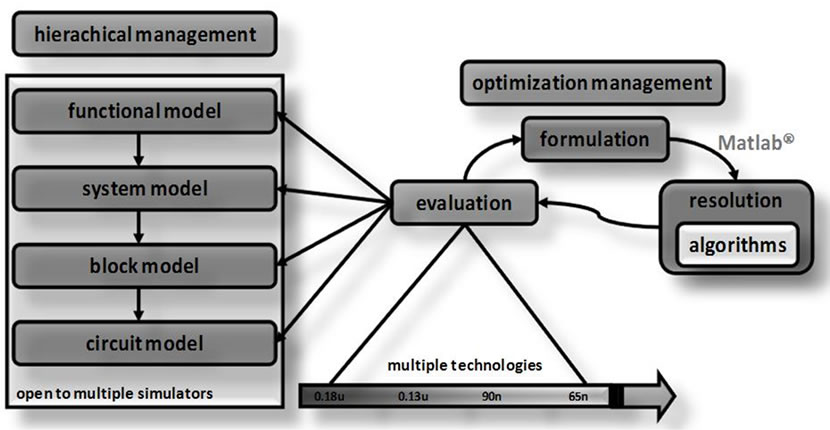
Figure 2. RUNE optimization steps.
• A cost function is formulated from specifications and design parameters set and stored in XML files.
• A design plan is set to define which optimization algorithms will be used to perform synthesis.
• A model at a given abstraction level for each specification must be defined for the performance evaluation during optimization process.
From the set of information provided by the designer, a multi-objective optimization problem is automatically formulated and run using the aggregation approach [8]. This is the formulation step, which consists in defining the objectives and the constraints of the problem, as well as the variables and parameters, their ranges and initial values. The implementation of this step is set up to use either MatlabÒ or an algorithm directly implemented in RUNE such as genetic algorithms, simulating annealing, Hooke and Jeeves, sequential quadratic optimization and pattern search algorithm. The evaluation method called during the optimization process can use a model from any abstraction level, since RUNE can call various simulators to perform an evaluation through its standard API. For example in the electrical domain, a given block can be described at circuit level (schematic representation) and its performance metrics can be evaluated with electrical simulation tools such as Spectre or Eldo, with various target technologies. The ability to use different models and tools, and to manage heterogeneity, plays an important role in the definition of complex design, as will be seen in the following section describing an application example.
3. Hybrid GA-SQP Algorithm
We have seen in the previous section that RUNE platform allows selection of several algorithms to perform optimization of complex circuits. We describe in the following part the candidate algorithms that will be used in our hybrid approach.
3.1. Genetic Algorithm
Genetic Algorithms are based on natural genetic and natural selection mechanism and some fundamental ideas are borrowed from Genetics in order to artificially construct an optimization procedure. The GA acts over a population of potential solutions, applying intensification (crossover) and diversification (mutation) operators to explore the problem space. The fittest individuals are selected and give birth to a new population, in the hope of improving the solution quality. GA is extensively discussed in the literature and details on its mechanisms can be found in [1]. The GA used in this study is part of the MATLAB optimization toolbox. The GA is configured to use heuristic crossover, roulette wheel selection and adaptive feasible mutation (detailed in the Table 1). The generation and the population values used for GA are set respectively to 5 and 10.
3.2. Sequential Quadratic Programming (SQP)
Sequential quadratic programming (SQP) [5,9] is one of the most popular and robust algorithms for nonlinear continuous optimization. It starts from a single point and finds a solution using the gradient information. SQP requires a reasonable starting solution to increase the opportunity to achieve an acceptable solution and to avoid the local optima. This algorithm allows to closely mimic Newton’s method for constrained optimization just as is done for unconstrained optimization. Each iteration contains an approximation made of the Hessian of the Lagrangian function which uses a quasi-Newton updating method. This is then used to generate a Quadratic Programming (QP) subproblem whose solution is used to form a search direction for a line search procedure. Sequential Quadratic Programming is an iterative method. It allows solving at the kth iteration a QP of the following form:
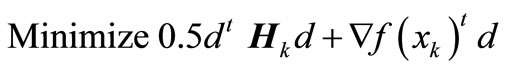 (1)
(1)
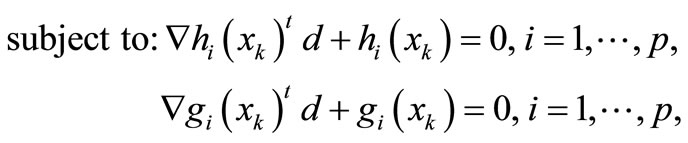
d is defined as the search direction and Hk is a positive

Table 1. GA configuration.
definite approximation to the Hessian matrix of Lagrangian function of the problem. The Lagrangian function can be described as:
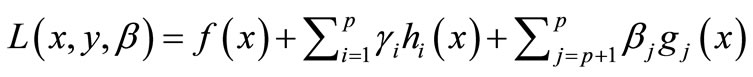 (2)
(2)
where γ, β are the Lagrangian multipliers. The active set strategy allows to solve the developed QP.
According to Equation (3), the solution xk is updated at each iteration.
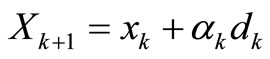 (3)
(3)
α is defined as the step size and takes values in the interval [0, 1]. After each iteration the matrix Hk is updated based on the Newton Method. The SQP used in this study is part of MATLAB tools.
3.3. Proposed Hybrid Approach: GA-SQP
Most of the studies on analog design automation process have focused on many optimization algorithms that have insisted on global search heuristics. However, the simultaneous use of local and global search techniques considerably improve the accuracy of results while reducing computational effort. Our proposed method therefore is an optimization algorithm combining a GA with a SQP algorithm, in order to solve analog circuit sizing problems. The GA algorithm is a global algorithm, which is well for a global search but performs very slow and very poor in a localized search. The SQP algorithm, on the contrary, has a strong ability to find local optima for constrained nonlinear optimizations problems, but it cannot guarantee that the solution is the global optimum of the problem. It ensures computational robustness when it starts from a feasible initial solution. By combining the GA with SQP, a new algorithm referred to as GA-SQP hybrid algorithm is formulated in this paper. First, GA searches the global optimum in the whole solution region in order to obtain a quasi-optimal solution. Then the global optimal solution can be obtained by SQP. This SQP significantly increases the power of the GA in terms of solution quality and speed of convergence to the best solution. The proposed hybrid method allows eliminating the need to provide a suitable starting point and allows ensuring a faster convergence speed and a higher convergence accuracy to find the optimal solution. The flow chart of the proposed GA-SQP algorithm can be summarized as follows (Figure 3).
4. Optimization Results of the TIA and Driver Circuits
Optical Network-on-Chip (ONoC) is a technology for
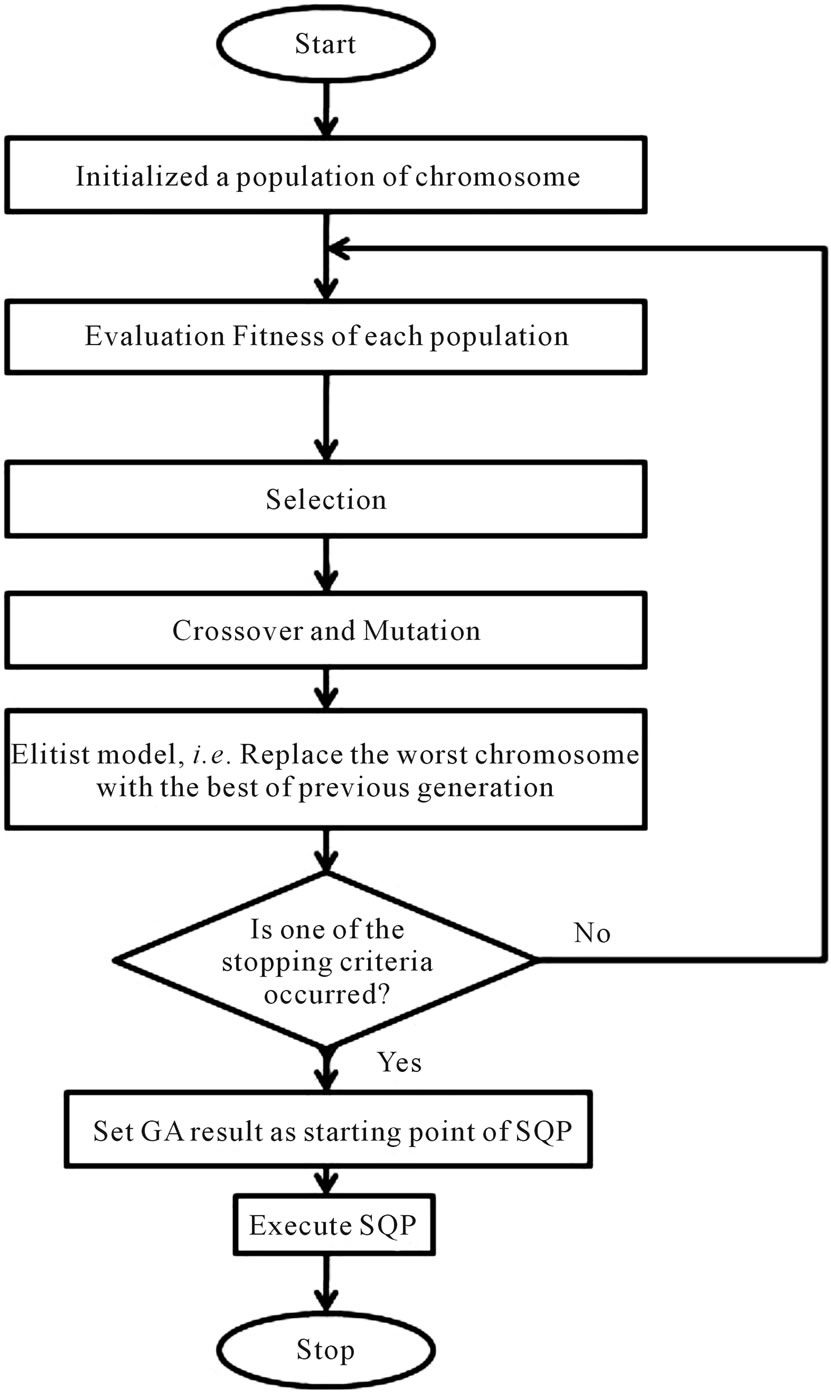
Figure 3. Flow chart of the proposed hybrid method.
high speed communication inside a single chip (a systemon-chip) [10]. Instead of transmitting data via metallic routes, an ONoC converts electrical signals to light pulses and transmits them through a dedicated network of optical waveguides (λ-router). An ONoC is a multidomain system, composed of digital elements for data flow control and analog and optical blocks to convert and modulate data as light impulsions. Together, these blocks compose transmission and reception interfaces with whom processors, memories and other intellectual property (IP) blocks can communicate.
In this paper we are interested only in the synthesis of the analog circuits of ONoC such as a transimpedance amplifier (TIA) used for reception and an optical driver (Driver) used in transmission, as illustrated in Figure 4. We used RUNE to optimize these circuits. The type of evaluation used for each performance, is based on equations and electrical simulations. The technology used for the design of both the circuits is a CMOS 0.35 µm.
These two examples of application are given in order to show the effectiveness of the proposed GA-SQP to solve analog circuits design problems. The first application concerns a mono-objective problem. That issue deals with optimizing the sizing of driver circuit to meet fixed specifications with two nonlinear equality constraints. The second application is about a multi-objective problem using the aggregation approach, and consists of sizing a TIA circuit with nonlinear inequality and nonlinear
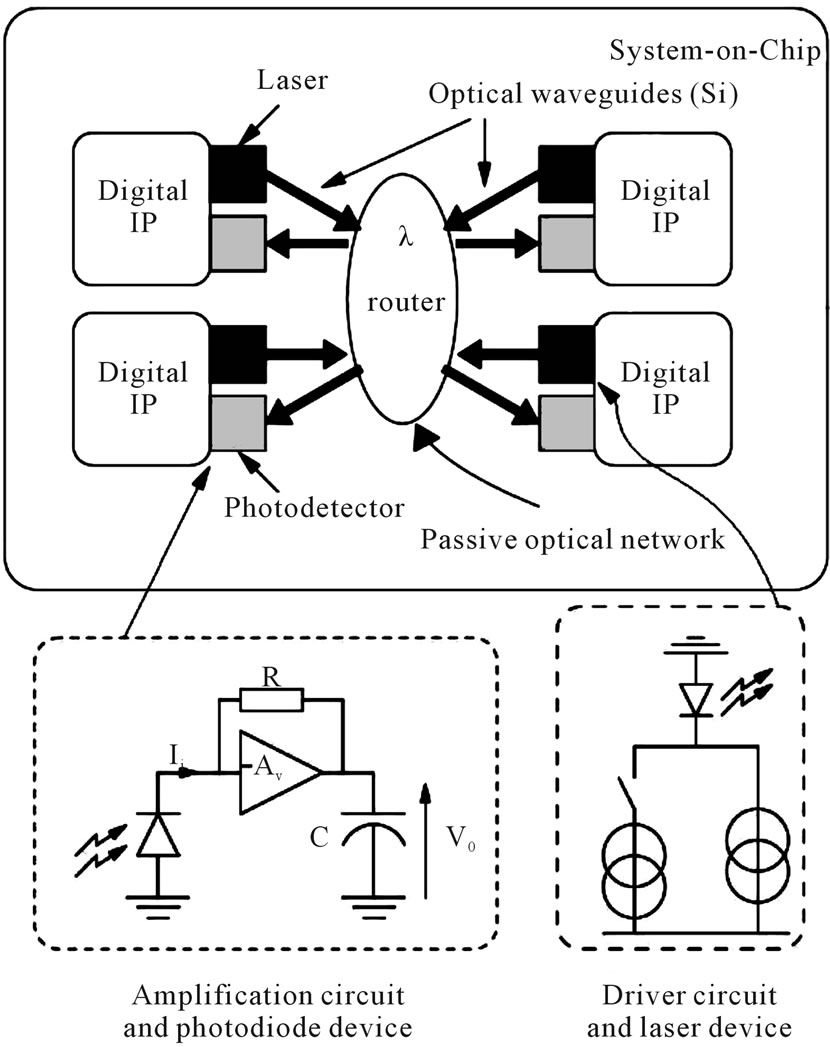
Figure 4. Multi-domain ONoC description [10].
equality constraints. Then, the performance of the proposed GA-SQP algorithm is compared to SQP. All the experiments were run under a Linux environment on an Intel Xeon machine (2.6 GHz, 8 GB of RAM, 4 CPU).
4.1. Optical Driver
An optical driver is a circuit used to modulate information as a light signal. In the case of our ONoC system, the driver circuit (Figure 5) converts binary data into two current intensities, which in turn drive a laser beam.
The design problem of this circuit consists of minimizing the area of the transistors, while keeping the output current at levels required by the laser (bias and modulation currents). The optimization variables are the width (Wi) and length (Li) of each transistor (Mi), which dictate their electrical behaviour. The area objective can be calculated by the product of the widths and lengths of each transistor, while the output current values come from the electrical simulator. In this case study, the problem is formulated as follows, with two equality constraints and that ensure proper functioning of the circuit in our target technology.

where X is the vector composed by the input variables (W1, L1, W2, L2, W3, L3, W4 and L4). The variation range of the optimization variables of the vector X are set as shown in Table 2.
The results obtained with GA-SQP are shown in Table 3. The transistor sizes for this optimal solution are listed in Table 4. Results show that the algorithm allows reaching the objective while respecting the nonlinear equality constraints.
4.2. Transimpedance Amplifier (TIA)
The Transimpedance Amplifier (TIA) is used in the receiver side of the ONoC. The incoming light signal is
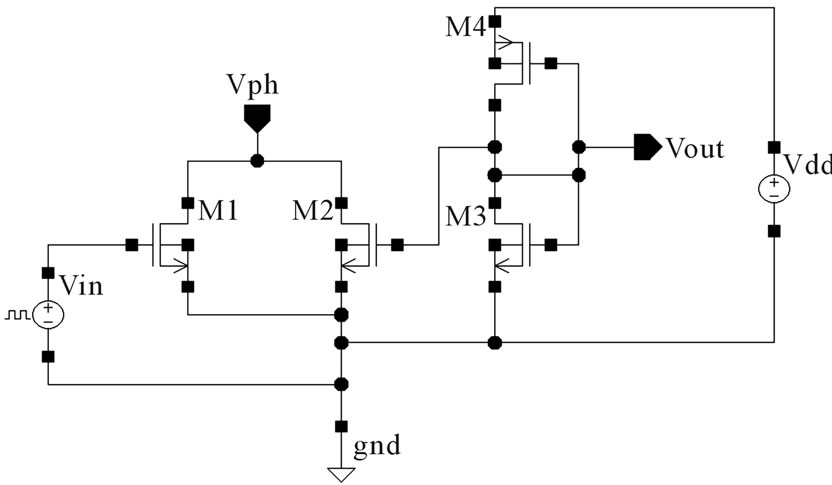
Figure 5. Circuit of the optical driver.
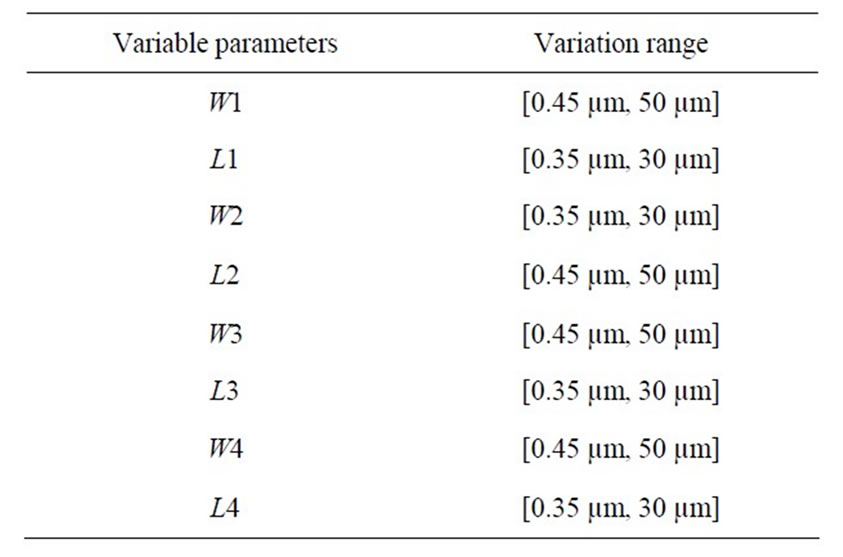
Table 2. Parameters values of the driver.

Table 3. Driver specifications and results.
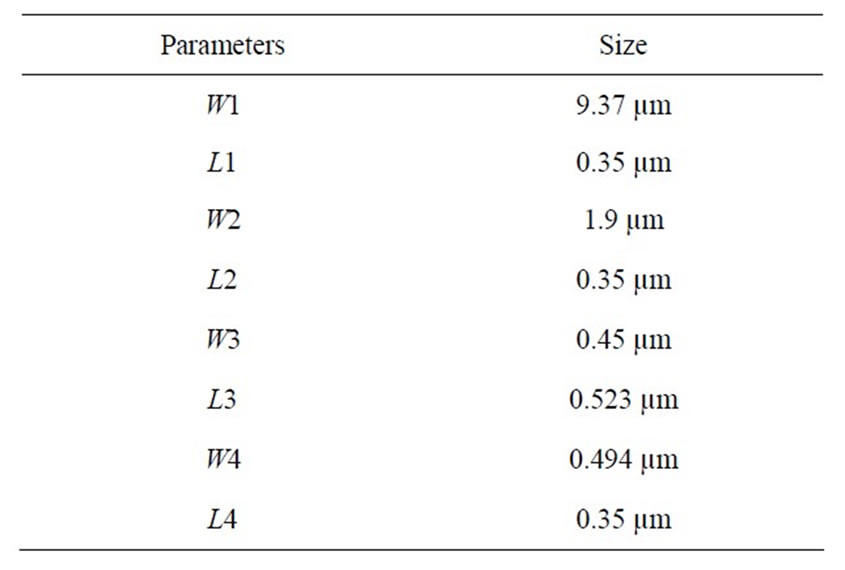
Table 4. Results of parameters sizing.
converted to current by a photodetector, and the role of the TIA is to convert this weak current signal to a voltage level that can be used in a digital circuit. The structure of the TIA, with its internal inverter amplifier, is illustrated in Figure 6.
The desired TIA performance criteria are: the transimpedance gain Zg, the bandwidth BW, the quality factor Q, the power consumption pwr and the transistors surface Area. Zg, BW and pwr are evaluated with the electrical simulator “Spectre”. Q and Area are evaluated with respectively the Equations (4) and (5).
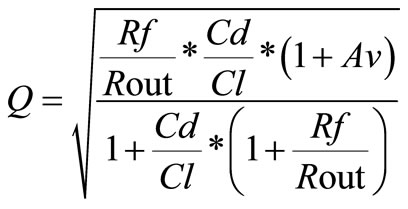 (4)
(4)
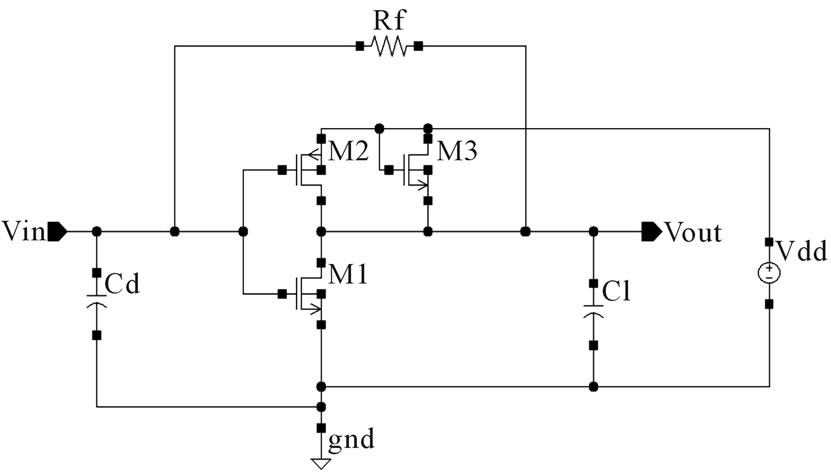
Figure 6. Circuit of the TIA.
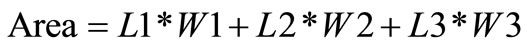 (5)
(5)
where, Rout and Av are, respectively, output resistance and gain of internal amplifier. They are evaluated with electrical simulations.
The purpose consists in optimally sizing TIA circuit with maximizing Zg and BW. We transformed these multi-objective problems into a mono-objective using the aggregation approach. There are two nonlinear inequality constraint such as pwr and Area and one nonlinear equality constraint such as Q.
The problem can be formulated as follows:

where X is the vector composed by the input variables (W1, W2, W3, Rf, Cd and Cl). The transistor length is fixed at 0.35 µm for all transistors and the variation range of the optimization variables of the vector X are set as shown in Table 5.
Table 6 presents TIA specification and best results of GA-SQP algorithm for 52 runs. Results of parameters sizing with GA-SQP algorithm are shown in Table 7. Results show that the algorithm allows reaching the objectives while respecting the nonlinear inequality and equality constraints.
4.3. Comparing GA-SQP to SQP
To show the effectiveness of hybrid optimization method, the proposed GA-SQP algorithm is compared to SQP. For this analysis we have collected, for both algorithms, runtime and fitness data over several independent runs of the TIA circuit optimization problem. A random multi start approach is used with the SQP algorithm to make comparison with GA-SQP which does not depend on its starting point. In all experiments, the stopping criteria of both algorithms are set to the same value. It takes into

Table 5. Parameters values of the TIA.
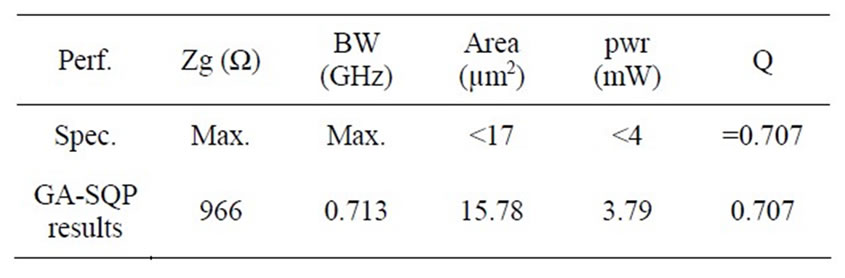
Table 6. TIA specifications and results.

Table 7. Results of parameters sizing with GA-SQP.
account the maximum number of iterations, the termination tolerance for the objective function value and the termination tolerance for the nonlinear constraints. The main input parameters of SQP and GA-SQP are indicated in Table 8.
GA-SQP and SQP algorithms have been executed 52 times. As shown in Table 9, GA-SQP algorithm allows to obtain 82.76% success solution and SQP algorithm allows to obtain only 18.29% success solution. Table 10 shows that the GA-SQP outperforms SQP in terms of the best and mean cost for success solution obtained during our tests. The gain of GA-SQP compared to SQP in terms of mean and minimum are respectively 25% and 13%. It clearly shows that the GA provides a good starting point to the SQP method more efficiently than a simple random start. Moreover, Table 11 shows that the GA-SQP consumes less time compared to SQP, because it requires less iteration to find the optimal solution.
In the hybrid GA-SQP, the initial search based on the use the GA does not require the user to provide such a starting value as the search is performed automatically. The results demonstrate that the proposed hybrid method
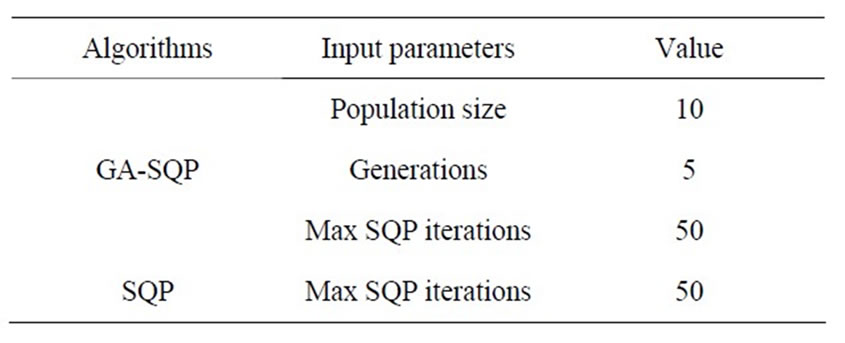
Table 8. SQP and GA-SQP input parameters.

Table 9. Success rate of GA-SQP and SQP.
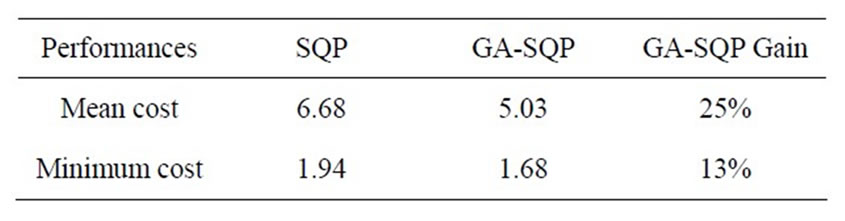
Table 10. Minimum and mean cost comparison.
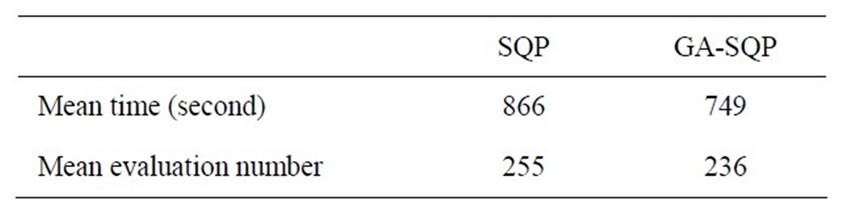
Table 11. Mean execution time comparison.
outperforms the SQP in terms of better optimal solution and significant reduction of computing times. The result for computational run time is impressive, because the combination of two algorithms consumes less than one. This explains that the genetic algorithm converges quickly to a near optimal solution, which allows to the SQP algorithm to find the optimum result with less effort.
5. Conclusion
We proposed a method based on a combination of GA algorithm and successive SQP algorithm, namely GASQP. It is implemented in the framework RUNE to optimize performances of analog circuits. GA-SQP seems to be suitable for solving both nonlinear mono-objective and multiobjective optimization problems. The results of the proposed hybrid method were compared with SQP algorithms to solve a TIA sizing problem. The results show that the proposed hybrid method outperforms the SQP in terms of better optimal solutions and signficant reduction of computing time. Furthermore, the hybrid GA-SQP algorithm does not require the user to specify the starting point. Finally, the proposed approach let us conclude that depending on the nature of our analog sizing problem (degrees of freedom, number of performances), efficient hybrid combination between an evolutionary approach and a direct search can be found.
REFERENCES
- G. Renner and A. Ekárt, “Genetic Algorithms in Computer Aided Design,” Computer-Aided Design, Vol. 35, No. 8, 2003, pp. 709-726. doi:10.1016/S0010-4485(03)00003-4
- M. Taherzadeh-Sani, R. Lotfi, H. Zare-Hoseini and O. Shoaei, “Design Optimization of Analog Integrated Circuits Using Simulation-Based Genetic Algorithm,” Proceedings of International Symposium on Signals, Circuits and Systems, Iasi, 10-11 July 2003, pp. 73-76.
- A. Jafari, M. Zekri, S. Sadri and A. R. Mallahzadeh, “Design of Analog Integrated Circuits by Using Genetic Algorithm,” Proceedings of International Conference on Computer Engineering and Applications, Bali Island, 19-21 March 2010, pp. 578-581. doi:10.1109/ICCEA.2010.118
- C. Wang, Q. Wang, H. Huang, S. Song, Y. Dai and F. Deng, “Electromagnetic Optimization Design of a HTS Magnet Using the Improved Hybrid Genetic Algorithm,” Proceedings of Asian Conference on Applied Superconductivity and Cryogenics, Miyazaki, 12 December 2004, pp. 349-353.
- N. Menezes, R. Baldick and L. T. Pileggi, “A Sequential Quadratic Programming Approach to Concurrent Gate and Wire Sizing,” Proceedings of International Conference on Computer-Aided Design, San Jose, 5-9 November 1995, pp. 867-881.
- L. Labrak and I. O’connor, “Heterogeneous System Design Platform and Perspectives for 3D Integration,” Proceedings of 21st IEEE International Conference on Microelectronics, Marrakech, 19-22 December 2009, pp. 161-164.
- F. Tissafi-Drissi, I. O’Connor and F. Gaffiot “RUNE: Platform for Automated Design of Integrated Multi-Domain Systems Application to High-Speed CMOS Photoreceiver Front-Ends,” IEEE Proceedings of Design, Automation and Test in Europe Conference, Paris, 16-20 February 2004, pp. 16-21.
- E. G. Talbi, “Metaheuristics: From Design to Implementation,” John Wiley and Sons Ltd., Hoboken, 2009.
- P. T. Boggs and J. W. Tolle, “Sequential Quadratic ProGramming for Large-Scale Nonlinear Optimization,” Journal of Computational and Applied Mathematics, Vol. 124, No. 1-2, 2000, pp. 123-137. doi:10.1016/S0377-0427(00)00429-5
- E. Drouard, M. Briere, F. Mieyeville, I. O’Connor and X. Letartre, “Optical Network On-Chip Multi-Domain Modeling Using System C,” Proceedings of the Forum on Specification and Design Languages, Lille, 13-17 September 2004, pp. 123-135.

