ABSTRACT

This paper presents keystroke dynamics based authentication system using the information set concept. Two types of membership functions (MFs) are computed: one based on the timing features of all the samples and another based on the timing features of a single sample. These MFs lead to two types of information components (spatial and temporal) which are concatenated and modified to produce different feature types. Two Component Information Set (TCIS) is proposed for keystroke dynamics based user authentication. The keystroke features are converted into TCIS features which are then classified by SVM, Random Forest and proposed Convex Entropy Based Hanman Classifier. The TCIS features are capable of representing the spatial and temporal uncertainties. The performance of the proposed features is tested on CMU benchmark dataset in terms of error rates (FAR, FRR, EER) and accuracy of the features. In addition, the proposed features are also tested on Android Touch screen based Mobile Keystroke Dataset. The TCIS features improve the performance and give lower error rates and better accuracy than that of the existing features in literature.

Keywords:

Information Set Theory, Two Component Information Set Features, Support Vector Machines (SVM), Random Forest, Convex Hanman-Anirban Entropy Function, Hanman Classifier, Convex Entropy Based Classifier

1. Introduction

Security is a concern since the advent of the computers. The need of robust and ubiquitous security systems is more apparent due to widespread use of Internet and rapidly growing online business transactions, e-banking, shopping, social interactions, emails to name a few. User authentication involving both identification and verification has become a necessity before the access to system resources is allowed. The most common user authentication system till date employs username and password/PIN. Irrespective of whether a user chooses a very easy password or forgets any password he has chosen; the system may be prone to misuse in either case. It is possible to steal or hack the most difficult password by means of brute force methods. Use of biometrics for personal authentication is becoming more acceptable these days because it is convenient to use and there is no issue of getting lost like smart cards and no problem of getting forgotten like passwords/PINs. Biometrics deals with physiological or behavioral human traits for authentication of a user. Biometrics provides significant security compared to username/password, smartcards etc. Among biometric traits, keystroke dynamics is most convenient since keyboard is available in most of the computer systems and does not require a special device like other biometric modalities such as fingerprint, palmprint etc. Keystroke dynamics based authentication is concerned with analyzing the human typing rhythm and behavior. Further keystroke dynamics is difficult to conceal and disguise just as human behavior is difficult to copy. Keystroke Dynamics can also be implemented on a network or distributed architecture.

1.1. Background Research

Keystroke dynamics based authentication system is dependent on the individual typing pattern. It is mainly based on how a user types rather than what the user types on keyboard. It measures human typing characteristics which are shown to be unique to an individual and difficult to be copied. In keystroke dynamics, there are mainly two metrics, Dwell Time which is how long a key is pressed and the other is Flight Time which is how long it takes the user to move from one key to the other. As the user types, an application running on the system captures the keystroke dynamics features flight time and dwell time.

There are some publicly available keystroke datasets. Most of these datasets prefer static text entry, for which a user is asked to type a predetermined text string. Some of the static entry dataset are from: Killorhy and Maxion [1] , Giot et al. [2] , Loy et al. [3] [4] . Very few datasets like Biochaves [5] , Clarksons University Keystroke Dataset [6] are based on free text.

Keystroke Dynamics features mainly include: Keystroke Latencies, Dwell Time and Flight Time. Gaines et al. [7] employ inter-key latencies from 87 lowercase letters to compute the means of the keystroke latencies and check their similarity. Young and Hammon [8] have used keystroke latency, keystroke pressure and total time to type as features for their experiments. They have built a template using these features. To authenticate a test feature vector, the mean timing vector and inverted covariance of timing vectors are computed [9] , and then compared statistically with the test timing vector. Joyce & Gupta [10] have augmented the login process by asking for user’s first name and last name in addition to the usual procedure of asking login name, password and latency information as feature subset. For recording the timestamp, special scan codes are used in the interrupt handler of the standard keyboard. When two keys are pressed such that the first key is not yet released and the second gets pressed, then a negative time measurement occurs which is a limitation. To overcome this, a modified latency measurement is suggested in [11] . A combination of key hold time and digraph latency metrics is used in [12] to reduce error drastically. The features used in [6] are of four types: key code (ASCII code of the key being pressed) and three timing features that include: Down-Down Time (DD), Up-Down Time (UD) and Down-Up Time (DU). The first two timing features are used to denote the inter-key latencies and third feature indicates the hold-time.

For authentication that involves both identification and verification of a user by keystroke dynamics based system, many classifiers have been used. They are divided into three broad categories, viz., statistical methods, neural networks and pattern recognition based techniques.

The statistical methods related to the first category employ statistical tools on basic keystroke features and apply distance metric to authenticate a user. The initial work on Keystroke Dynamics by Gaines et al. [7] involves t-test on diagraph features to check the similarity of mean vectors and covariance matrices on two multivariate normal populations giving FAR of 0% and FRR of 4%. But this is impossible to achieve in real life situation where the number of users is very less. Umphress and William [13] identify a user by comparing the keystroke latencies and digraphs of the test sample with the reference profile data comprising the mean keystroke latency and average time to press in the two consecutive keys. A confidence score is specified to achieve FAR of 17% and FRR of 30%. Joyce and Gupta [10] have developed a mean reference signature consisting of a set of four vectors of keystroke latencies for username, password, first name and last name. The norm is computed between the test keystroke pattern and the reference signature and then the user authentication is done based on some predefined threshold. By this FAR of 0.25% and FRR of 16.67% are achieved. Teh et al. [14] have proposed a statistical fusion approach for keystroke dynamics based recognition system and they authenticate a user using the weighted sum of Gaussian scores and Direction Similarity Measure based scores.

We now detail out the neural network based approaches under the second category. Giroux et al. [15] have used keypress ratios as a measure of authentication and a dedicated Artificial Neural Network (ANN) is employed for the authentication of a user. A function f: R^m−1 à {−1, 1} is learned from ANN, where x ϵ R^m−1 denotes the m − 1 keypress interval timing ratios for m-character password and f(x) = [−1, 1] indicates whether the input keypress interval ratios correspond to that user or not. For every individual, a feed-forward ANN is trained with back-propagation, resulting in weights that are subsequently used for authentication. Bleha et al. [16] have used linear perceptron to authenticate the users and reported error rates, FAR and FRR of 9% and 8% respectively. The use of two separate orthogonal digraph components - Keystroke duration and Keystroke latency are found to provide significant predictive power with Back- Propagation Model [12] . To attain IPR of 0% and FAR of 11.5%, a preprocessing step is performed.

The pattern recognition based techniques falling under the third category are now discussed. Support Vector machine (SVM) based on keystroke latency in [17] gives FAR of 0.02 and FRR of 0.1 for 10 users. The keystroke latency and key hold time are used as features for k-nearest neighbor classifier in [18] . The classical pattern recognition based algorithms such as back propagation with sigmoid transfer function, sum of products, hybrid sum of products, Bayes’ decision theory and Potential Function are used in [19] for combining key hold time and interkey latencies. Among various pattern recognition techniques used in [19] , potential function gives the best results with FAR and FRR of 0.7% and 1.9% respectively.

1.2. Motivation for the Present Work

From the literature survey, it can be seen that most of the approaches on keystroke dynamics are carried out on the created datasets and they report results either on desktop or mobile but not both. It is difficult to compare the performance of different approaches due to lack of common benchmark dataset. So, we have tested the proposed approach on the benchmark datasets under both desktop and mobile environments and the results obtained are found to be superior to the best so far.

The organization of the paper is as follows: Section 2 presents the information set (IS) and some of its properties. It also formulates the IS based features and higher form of IS features. Section 3 develops an algorithm for the two-way information set approach. Section 4 describes the databases for the present work and Section 5 discusses the results of implementation. Section 6 gives the conclusions and the future work.

2. An Introduction to Information Set

A fuzzy set deals with vagueness or fuzziness [20] . It is characterized by a membership function (MF) that maps the information source values to the degree of association in the range (0, 1). The MF of x_i in a fuzzy set (F) is denoted by μ_F(x_i). Given a collection of attribute values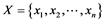, F is a set of ordered pairs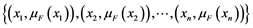. A fuzzy set suffers from some drawbacks [21] : i) The values of MF are separate from the information source values. There is no way to link the two into a single entity. ii) MF doesn’t provide the overall fuzziness/vagueness of F but only the degree of association of every information source value to a vague concept, and iii) The time varying information source values are not easily represented in MF. To eliminate these drawbacks of a fuzzy set, Hanmandlu and his co-works have developed Information set theory which can be found in [21] - [27] based on the information theoretic entropy function christened as Hanman-Anirban entropy function. The properties of information sets given later in this section will highlight the power of information sets.

Our primary goal being the representation of overall uncertainty in keystroke dynamics, we are inclined to investigate the suitability of the information set based features. We will now discuss how a fuzzy set paves the way for the information set while representing the uncertainty in its elements using an entropy function.

2.1. Information Set Concept

Consider a set of keystroke timing features T = {T_ij} where T_ij is the j^th feature in i^th keystroke sample. When a set of keystroke timing features is fitted with a membership function, denoted by {μ_ij}, a pair of keystroke timing value and its membership function forms an element in a fuzzy set. Information set connects the two components of each pair into a single entity called the information value using the Hanman-Anirban Entropy function [22] which has the facility to represent both probabilistic and possibilistic uncertainties. The probabilistic uncertainty in a fuzzy set is defined by Hanman-Anirban entropy function having a polynomial in its exponential gain function as:

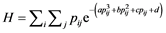(1)

where,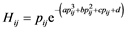

and a, b, c and d are real valued parameters which need to be selected appropriately. It may be noted that p represents the probabilities. As shown in [23] that the possibilistic uncertainty is a better representation of uncertainty than the probabilistic uncertainty given by Equation (1). Moreover, the number of probabilities is limited in the context of keystroke dynamics; this is the reason we are bent upon exploring the possibilistic uncertainty.

To bring Equation (1) into the information set domain, let us call the keystroke timing features T_ij as the information source values. We then replace the probability p with T_ij in Equation (1) and convert the exponential gain function into the Gaussian membership function by selecting the parameters as,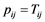

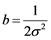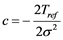, , , leading to:

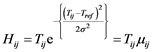(2)

A more general entropy function is presented by Mamta and Hanmandlu in [24] . This entropy function not only converts the exponential gain into the generalized Gaussian membership function with an exponent power of but also modifies the information source values with a power of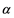. This is defined as:

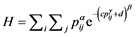(3)

where

By taking and, , Equation (3) becomes

(4)

The product of Information source value and membership function is termed as the information value and this is more general than the one in Equation (2). The sum of all information values, gives the effective information. In this work, we are using only the information value as a feature.

Definition of Information Set: A set of information values is called the information set such that each information value is a product of the information source value and the corresponding membership function value. The values of and need to be selected appropriately.

2.2. Some Properties of Information Sets

The properties of information sets are presented in [25] . Following are the important properties of Information Sets:

1) The membership function can be empowered to act as an agent with the capabilities that are beyond the scope of a fuzzy set. For example, the complement of a membership function can be an agent. Any intuitionist membership function can also be a contender. The membership function can be formed from other information source values not associated with the same fuzzy set. Thus, an agent extends the scope of a fuzzy set.

2) The higher form of information sets called transforms can be derived based on the information values. This is shown in the sequel.

3) The information set arises out of representing the varying information source values in either time or space. For example, a variation in the keystroke data within a sample gives the spatial information values whereas the variation in keystroke timings over a number of samples gives the temporal information values.

4) Information set can represent both probabilistic and possibilistic uncertainties. To represent the probabilistic uncertainty, frequencies of occurrence of the information source values called the probabilities are considered but for the possibilistic uncertainty, attribute values like keystroke timing values are considered.

2.3. Derivation of Information Set Based features

We will now derive the information set based features. The use of basic information set features like sigmoid and energy appears in [26] . It is important to note that our unit of information is either the information value or the complement information value.

a) Information Value

The basic information values can also be used as one of the features in our study. The membership function is taken to be Gaussian with:

(5)

where the reference, is the average of values. One can take any value such as mean, maximum and median for the reference.

b) Complement Information Value

As per the second property of information sets stated above the complement of membership function, i.e., is found to be useful as an agent which is an empowered membership function with an extended scope as compared to that of a fuzzy set. As a result, the complement information value serves as the feature, given by

(6)

where. Note that the complement membership function has its domain out of the fuzzy set.

c) Energy features

As the information value depends on the membership function empowered as an agent, we can generate different kinds of information values by changing the agent. To generate Energy feature, the agent is taken as:

(7)

So, the complement energy feature is:

(8)

d) Sigmoid feature

According to the first property of information set, information value () considering it as a unit of information can be modified by applying some function like sigmoid function. Note that the effectiveness of the information value (feature) gets enhanced with the application of this function. So, the modification of information value using the sigmoid function leads to the sigmoid feature defined as:

(9)

e) Multi Quadratic feature

The multi-quadratic function either increases or decreases monotonically from the center. Using this function, the membership function is computed as:

(10)

where is a fuzzifier given by. The multi quadratic information value is computed as.

f) Inverse Multi Quadratic feature

Inverse multi-quadratic function is the reverse of multi-quadratic function. Membership function for the inverse multi quadratic feature is given by

(11)

The inverse multi-quadratic information value is therefore.

2.4. Higher Form of Information sets

So far, we have utilized the basic information values for deriving different features. We will now derive higher form of information set based features. This requires us to consider the adaptive Mamta-Hanman entropy function in which the parameters of the exponential gain function are assumed to be variables. Some important properties of this adaptive entropy function are relegated to Appendix A.

a) Hanman Transform

Hanman Transform is a higher form of information derived from the adaptive Mamta-Hanman entropy function in [24] . The use of this transform appears in [27] . The idea of this transform is to use the first-level information values in getting the second-level information values. Thus, this transform is intended to get a better representation of the uncertainty in the information source values. The Hanman Transform (HT) is defined as

(12)

where

Proof: By taking, , , and in (3) we obtain (12).

Note that the exponential gain function has its argument as the first-level information value and after evaluation using Equation (12) we get the second-level information value. This is called transform because the original Information source value is modified by the information value,.

The Complement Hanman Transform is easily obtained by setting in the above proof as

(13)

b) Shannon Transform

Shannon Transform is an offshoot of Hanman Transform as it can only be derived from the Hanman Transform and its features are shown to be useful in the face recognition in [22] . The Shannon transform (Sh) features are computed from:

(14)

Proof:

Again, we resort to the adaptive Mamta-Hanman entropy function (3) and set, and leading to

(15)

where

This is Pal-Pal transform. This can be shown to be equivalent to what we term as the non-linear Shannon transform in Equation (14) where the logarithmic function is operating on the information values. In some applications, the use of complement of μ_ij in the transform improves its effectiveness. The Shannon inverse transform where the evaluation of the information source values is based upon the complement agent is expressed as:

(16)

In the above transforms, Gaussian membership function as defined in Equation (5) is best suited. These transforms can have realistic applications in social networks though not attempted so far. For example, we gather information about an unknown person of some interest to us. This is the first-level of information and then evaluate him again to get the second-level of information camped with the first-level of information. They can be used to evaluate not only the information source values but also the membership function values to see whether the selected membership function is appropriate.

c) Composite Transform

For creating sigmoid and energy features, we have considered the basic information value as the unit of information. But to create the composite transform consider the Hanman transform feature as the unit of information and apply the log function on it leading to the composite transform given by

(17)

In fact, this is the ij component of the following transform:

(18)

By interchanging log and exponential function we can formulate yet another composite transform as given by

(19)

As can be noted that the difference between Equations (18) and (19) is that in the former case log function is applied on the Hanman transform whereas in the latter case the exponential function is applied on the Shannon transform. In this paper, we have shown the results of Equation (18).

The Complement Composite Transform is easily obtained by considering the complement Hanman Transform as the unit of information and applying the log function on it. It is given by

(20)

d) Convex Hanman-Anirban Entropy Function

Let be convex and twice differentiable function and is convex, twice differentiable and strictly increasing function. Then the generalized mean can be written as: [28]

(21)

where are such that,. Assuming

(22)

Its double derivative is therefore

. (23)

Supposing then

. (24)

If then. Substituting (24) in (21) yields the convex entropy function

(25)

If we take which is the unit of information in Equation (25), we obtain convex Hanman-Anirban entropy function:

(26)

We can find its use in the design of or to modify a classifier. Here we use it to modify the Hanman classifier.

3. Feature Extraction and Classifier Design

3.1. The Two-Component Information Set (TCIS)

We have at our disposal several samples of keystroke dynamics for each user. To calculate the membership function, we have adopted Two-Component information set approach. In this approach, the temporal information I₁ is the first component for which the membership function is computed using all the training samples. The spatial information I₂ is the second component for which the membership function is computed using all the features in a single sample. Concatenation of these two information components results in Two- Component Information Set features denoted by I. A flowchart shown in Figure 1 explains how the features are computed in both training and test parts. The features from these parts go to a classifier for the authentication of keystroke sample.

Algorithm:

Step 1: Compute mean and variance of all the training samples.

Step 2: Compute mean and variance of all the features in a single training sample.

Step 3: For each training sample, compute using and and then compute using and. These membership functions along with T give us two components, and.

Step 4: Concatenate I₁ and I₂ and generate new features such as Information, Energy, Sigmoid, Hanman Transform etc. Then train SVM/Random Forest classifier or Convex Entropy Based Classifier using these features.

Step 5: For each test sample, compute I₁ using and computed in Step 1.

Step 6: Compute mean and variance of all the features for the test sample. Compute I₂ using and.

Step 7: Concatenate I₁ and I₂ to obtain I and use the new features for the classification using SVM/ Random Forest classifier or Convex Entropy Based Classifier.

3.2. Design of Hanman Classifier (HC) Using Convex Entropy Function

As I is a feature vector, let us denote the training feature vector of r^th sample of l^th user by P_l(r, k) and Q(k) be the test feature vector where k refers to the k^th feature value. The training and testing feature vectors are subjected to min-max normalization. In view of Equation (25), the test feature vector is rewritten as:

(27)

Similarly, each training feature vector can also be denoted in the above form as:

(28)

a) Use of Conditional Entropy Function

The conditional Hanman-Anirban entropy termed here as conditional possibility, c poss of a test feature vector Q(k) given the training feature vector P_l(r, k) is expressed by following [25] as:

(29)

The conditional possibility of intersection of two training feature vectors given the test feature vector can be written as:

(30)

As t-norm being the conjunction operator it gives the minimum difference between any two vectors in (30) where we have used Frank t-norm for t_F as it is found to be most effective [24] . It is given by

(31)

We call as the normed error vector as it is the result of applying t-norm on the pairs of two error vectors. We now invoke the convex entropy function for the representation of uncertainty in the normed error vectors.

(32)

In order to improve the above convex entropy function, we convert it into parametric form:

(33)

where and are the parameters. The proof of (33) which is no longer a convex function can be given as follows: This entropy follows from Mamta- Hanman entropy function with proper substitution of parameters. Taking logarithm of this entropy function converts into a composite entropy function. From our experiments, we get the best results with and on keystroke dataset. We compute h(l) for all i, j and the minimum value associated with l gives the identity of the unknown user; so the criterion function is selected as:

(34)

4. Description of Databases Used

For the evaluation of the keystroke dynamics based authentication system, the following publicly available datasets are availed:

a) CMU Keystroke Dynamics Benchmark Dataset [1]

This database comprising 51 users is collected in 8 sessions and 50 repetitions of the same password are recorded in each session. We have 400 samples per user. CMU benchmark dataset has keystroke features, viz., DD (Down-Down) time, UD (Up-Down) time and H(Hold) time. A 10 character password (.tie5Roanl) is typed by a user. In our study, we have used H and UD since they give the best results. Accordingly, we have 21 features that include: 11 H values for 10 characters and an enter key, 10 UD values of time latencies between 11 key presses. Considering each of 51 users as both genuine and imposter we have a pool of 51x50 sets of experiments.

Half of feature vectors of every user in each session is treated as the training data and the remaining half as the positive test data, i.e. 200 samples each. In addition to this, the first 5 samples from each of the remaining users are assumed to be the negative test data in every experiment. As demonstrated in [29] that by including the background user’s data during the training phase in keystroke dynamics, the error rates are reduced significantly. Similarly, to train a classifier, we take the first 4 samples of the remaining users as negative training data resulting in 196 samples. The classifier is trained in each experiment such that samples of an imposter are not visible to the classifier during training.

The authentication accuracy is evaluated using EER (Equal Error Rate) where False Acceptance Rate (FAR) equals False Rejection Rate (FRR) on ROC curve. FAR is the rate at which an unauthorized person (i.e. imposter) would be given access to the system as a genuine user [30] whereas FRR is the rate at which an authorized user would be rejected the access to the system considering him as imposter. FAR is calculated as the ratio of imposters granted access to the total number of imposter attempts while FRR is calculated as the ratio of genuine users denied access to the total number of genuine attempts.

For SVM and Random Forest Classifier, the performance measure EER is calculated for each set of genuine and imposter users, i.e. 51 × 50 sets of such experiments. The mean of the performance measure values (EERs) is then calculated for all the experiments. In addition to EER we also report FAR and FRR values and authentication accuracy.

For convex entropy based classifier, the performance is reported in terms of EER(mean), FAR, FRR and Accuracy, calculated as the ratio of number of users correctly classified as genuine/imposter user to the total number of user attempts across all the experiments. FAR is calculated as the ratio of number of users which are incorrectly accepted as genuine to the total number of imposter user attempts across all the experiments. FRR is calculated as the ratio of number of users which are incorrectly rejected as imposter to the total number of genuine user attempts across all the experiments.

b) Sapientia University Keystroke Benchmark Dataset for Android platform [31]

This data is collected from 42 users with 51 samples per user with at least 2 sessions per user. Each user types the password “.tie5Roanl” on Android based Mobile Devices Nexus 7 Tablet and Mobil LG Optimus L7 II P710. The key sequence resulting from typing the password is “ti e [123?] 5 [abc] [Shift] R [Shift] o a n l” which are 14 key presses. We have used all of 71 features of the dataset given in Table 1 for our work.

For every user 45 samples are randomly selected as the training data and the remaining 6 samples constitute the positive test data. We take 1 sample from each one of the remaining users so as to have 41 negative test samples and include the first 2 samples of the remaining users who are neither genuine nor imposter in the training data resulting in 80 samples for the negative class as the imposter training data. Here again, each one of 42 users is considered as both genuine and imposter to conduct 42 × 41 sets of experiments. The classifier is trained on each of these experiments such that the samples of an imposter are unavailable to the classifier during training. Performance is then measured in terms of error rates EER, FAR, FRR and accuracy.

c) Classification of the proposed features

In our work, we have used three classifiers. The first is two-class SVM classifier with a linear kernel. The second classifier used is Random Forest Classifier, which generates an ensemble of decision trees based on the training data. Every test input vector is evaluated by all decision trees in the Random forest classifier

that operates on the principle of majority votes to get the classification vote. In addition to these standard classifiers the proposed convex entropy based classifier is third one discussed in Section 3.2.

5. Results of Implementation

Before presenting our results, let us see the state of the art on keystroke dynamics in the literature. Table 2 shows EERs for some of the algorithms with the best performance on the recent CMU dataset. The first algorithm given in Table 2 is an anomaly detector that uses Manhattan Distance [1] [32] . This method arrives at the mean of timing samples and the absolute mean standard deviation for each feature [32] . Given a test feature vector, a distance score is calculated using the following scaled Manhattan Distance:

(35)

where and are i^th test feature and i^th mean vectors respectively and is the mean absolute standard deviation of i^th feature.

Zhong et al. [33] have developed the new distance metric by combining both Mahalanobis and Manhattan distances as given by

(36)

where is the inverse of the principal square root of covariance matrix S.

Deng and Zhong [29] have used Deep Belief Networks by stacking together Gaussian RBM (Restricted Boltzmann Machine) with 31 visible units and 100 hidden units, and a binary RBM with 100 visible units and 100 hidden units, and obtained a mean EER of 0.035.

Table 3 shows the EERs obtained on SU dataset in [31] for two-class classifiers using all 71 features as shown in Table 1. These features also include touch based features such as finger area and key press pressure.

The performance of different information set based features with α = 1 on CMU dataset is listed in Table 4 in terms of FAR, FRR, EER and accuracy using

SVM. The best EER of 0.0201 is obtained with Information and Sigmoid features. The average ROC for various information set features with α = 1 on CMU dataset is shown in Figure 2 using SVM as classifier.

The features of Table 4 are applied on the same CMU dataset but with α = 2 using SVM and the results are given in Table 5. Here the best EER of 0.0225 is obtained with the Sigmoid Features. Comparing Table 4 and Table 5 we note that sigmoid feature is best in terms of EER values. The average ROC for various information set features with α = 2 on CMU dataset is shown in Figure 3 using SVM.

Table 6 shows the performance of Convex Entropy Based Classifier for different information set features with α = 1 in terms of FAR, FRR, EER and Accuracy. Table 6 shows the best performance for Information Feature in terms of EER of 0.0112 and accuracy of 0.9875. The average ROC for various information set features with α = 1 is shown in Figure 4. The features used in Table 6 are obtained with α = 2 for Convex Entropy Based Classifier and the results are shown in Table 7. Here we get the best performance in terms of EER of 0.0111 and accuracy of 0.9866 for Composite Transform. The average ROC with α = 2 is shown in Figure 5.

The features used in Table 4 and Table 5 along with the additional features contribute to EERs and accuracy figures in Table 8 on the same CMU data with α = 1 but with random forest classifier. In this case the best EER of 0.0103 is obtained with the Hanman Transform. The averages of ROCs for some of the features are shown in Figure 6.

The features shown in Table 8 are now obtained with α =2. Random Forest is used on CMU dataset and the results are given in Table 9. The mean ROC curves for some of these features are displayed in Figure 7.

The results of some of the features of Table 8 and Table 9 used on SU dataset with Random Forest for α = 1 are given in Table 10. By this classifier, the best EER is obtained with Information Value and Energy features. The Composite Transform lags these features in performance slightly. The average ROC for these features is shown in Figure 8.

These features are also tested with α = 2 on SU dataset with Random Forest

classifier and the results are shown in Table 11. The mean ROC for these features is shown in Figure 9. Best EER is obtained using Hanman Transform. Note that SVM and Convex Entropy classifier don’t perform well because of very

less data.

Discussion of Results: Out of 10 features, a subset of 6 features has been found to be effective on implementing two datasets: CMU and SU using three classifiers: SVM, Convex Entropy and Random Forest (Treebagger). The best results on CMU dataset are due to Composite Transform feature with EER of 0.0102 for Treebagger classifier and EER of 0.0111 for Convex Entropy classifier. The EERs obtained by the literature features (See Table 2) are inferior. On SU data, however Treebagger gives better result (EER of 0.228) with Energy feature than those of literature features in Table 3.

6. Conclusions

The possibilistic uncertainty in the keystroke timing values termed as information source values when represented by the entropy function gives rise to the information values which are shown to be the products of information source values and the corresponding membership function values. Two Gaussian membership functions are employed: one using the mean and variance of all the samples which lead to temporal information values and the other using the mean and variance of a single sample which lead to spatial information values. These two kinds of information values, viz., spatial and temporal components are concatenated to provide us the two-component information set (TCIS) features. From the concatenated features, various new features such as Information Value, Energy, Sigmoid, Hanman Transform, Shannon Transform, Multi-quadratic, Composite Transform and their complements are generated. In this work, Hanman Classifier is redesigned by the use of Convex Entropy Function.

TCIS features from two benchmark datasets CMU and SU are classified using Convex Entropy based classifier, SVM and Random Forest classifiers. Their performance is evaluated on the proposed features in terms of error rates (FAR, FRR, EER) and accuracy. These features are also tested on Android Touchscreen based Mobile Keystroke Dataset and the performance of these features outperforms that of the literature features.

We plan to extend this work by considering new features based on information set theory and type-2 and interval fuzzy sets. It is observed that the efficiency of feature type is dependent on database. Out of all the features investigated, Sigmoid, Energy, Hanman transform and Composite transform features have made their mark as the effective features. We have not attempted the fusion of the effective features. If these features are fused by either at the feature level or score level, then the fused feature vector is likely to outperform on all the datasets considered.

There are two limitations of the proposed approach. The first limitation is that it is not suitable for capturing global characteristics as its main forte is in local characteristics. The second limitation is the choice of membership function. Generally Gaussian function serves as an effective membership function.

Cite this paper

Bhatia, A. and Hanmandlu, M. (2017) Keystroke Dynamics Based Authentication Using Information Sets. Journal of Modern Physics, 8, 1557-1583. https://doi.org/10.4236/jmp.2017.89094

References

Appendix A: Adaptive Mamta-Hanman Entropy Function

Let us make H adaptive in (3) by considering the parameters as functions rather than constants as per the original definition in [24] . For simplicity, we consider the adaptive form of 1D H given by

(A.1)

In this the parameters and are assumed to be variables. The 1D form of this function [24] is:

(A.2)

where with. We will prove some important properties of the adaptive entropy function. In order to simplify proofs, we set α = 1.

Properties of Adaptive Entropy Function

1) is a continuous function for; so

is also a continuous function being a product of two continuous

functions and H being the sum of continuous functions is also a continuous function.

2) is bounded. As, is bounded for; so is H bounded.

3) With the increase in, decreases; so

as.

4) If then H is an increasing function of n.

(A.3)

(A.4)

Hence this is proved.

5) Note that is a concave function where and.

To prove that this is concave the Hessian matrix must be negative definite. The Hessian is computed as follows:

(A.5)

(A.6)

As c_i, p_i are in [0, 1].

(A.7)

and (A.8)

where, hence all the Eigen values of the Hessian matrix are negative. So, the Hessian is negative definite and H is concave.

6) Entropy H is maximum when all p_i’s are equal. In other words,

That is,

(A.9)

In that case,

(A.10)

7) The entropy is minimum if and only if all p_i’s except 1 are equal to zeros and single p_i = 1.

To make better representation of uncertainty, we will introduce higher form of uncertainty representation.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact jmp@scirp.org