Journal of Modern Physics
Vol.08 No.08(2017), Article ID:77403,6 pages
10.4236/jmp.2017.88076
General Relativity and the Theory of a Self-Interacting Abelian Gauge Field
Daniel Wisnivesky
Instituto de Física “Gleb Wathagin”, Universidade Estadual de Campinas-Unicamp, Campinas, Brazil

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 16, 2017; Accepted: July 1, 2017; Published: July 4, 2017
ABSTRACT
The standard theory of general relativity (GR) can be written in a form proposed by Eddington using the parametric representation of the metric tensor. In this paper, the equations of the standard theory of GR using the parametric representation are first developed. Afterwards, the fundamental ideas of a new type of abelian self-interacting gauge theory are presented. Finally, it is shown that the gauge field equations of this new theory are identical to the parametric form of Einstein’s equations of general relativity. It is concluded that classical gravity can be described either by the usual theory of GR in a curved space-time or, alternatively as a self-interacting gauge theory independent of the dynamics of space-time.
Keywords:
General Relativity, Gauge Theory

1. Introduction
Three of the fundamental forces in nature are described by Yang and Mills quantum field gauge theories on flat space-time, the fourth interaction, gravity, being a classical theory involving the dynamics of curved space-time is the exception.
The original theory of general relativity (GR) in terms of the metric tensor of curved space-time has been the subject of alternative formulations by different authors during the last 100 years. Some of these correspond to different versions of Einstein’s theory; others are theories that depart from Einstein’s while at the same time describing the known experimental results. Examples of the first type are: Schrödinger’s affine connection [1] ; Palatini’s metric-affine gravity [2] ; Tetrads local coordinate system [3] ; Tetrad field and a complex connection (loop- space gravity) [4] [5] [6] and Arnowitt, Deser and Misner’s foliation of space-time [7] , among others. A long list of alternative theories to GR can be found in the review paper by Clifton et al. [8] .
This situation is peculiar to GR, since nothing similar occurs with the other theories describing the fundamental interactions of matter. The theory of GR is 100 years old, and has successfully passed all experimental tests, making several predictions that had finally been confirmed. So what could explain the search for either different formulations or alternative theories? A possible reason could be the apparent incompatibility between GR and quantum field theory; another explanation may rest on the fact that GR is not a Yang and Mills gauge theory, while all other fundamental interactions are.
The purpose of this paper is to present classical GR under a new dressing which may disclose new properties of the theory and allow establishing a relationship with the other theories of the fundamental interaction of matter.
Eddington [9] , introduced the idea of representing the metric tensor of a four dimensional curved space-time in terms of ten parameters. In the first part of this paper, the equations of the standard theory of GR using the parametric representation of the metric tensor proposed by Eddington are worked out. In the second part the formalism of a self-interacting abelian gauge field is developed.
2. Parametric Form of Einstein’s Equations.
In the book “The Mathematical Theory of Relativity” [9] , Eddington mentions the possibility of representing the metric tensor of a four-dimensional curved space-time in terms of ten parameters. With this in mind, the equations of the standard theory of GR using the parametric representation of the metric tensor will next be developed.
Let 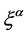 be the coordinates of a 10-dimmensional space with constant metric tensor
be the coordinates of a 10-dimmensional space with constant metric tensor 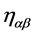 (
(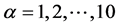 ). The line element in this space is given by:
). The line element in this space is given by:
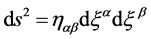 (1)
(1)
A four-dimensional continuum obeying Riemannian geometry can be repre- sented parametrically as a four-dimensional surface in the above mentioned space. Let xi (i = 0, 1, 2, 3) be the parameters on the surface, then the region can be mapped parametrically in terms of 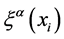 and the line element can be written as:
and the line element can be written as:
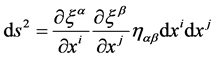 (2)
(2)
and the metric tensor of the curved Σ region is given by:
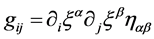 (3)
(3)
The rectangular matrix 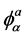 is defined in terms of the inverse metric
is defined in terms of the inverse metric 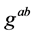 and
and 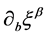 as:
as:
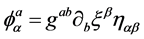 (4)
(4)
Then 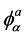 satisfies the relation
satisfies the relation
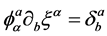 (5)
(5)
The inverse metric tensor can also be written as:
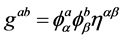 (6)
(6)
Next, the usual equations of GR are obtained in terms of 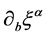 and
and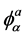 .
.
For the affine connection the normal expression for a torsion-free manifold is used,
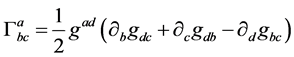 (7)
(7)
Substituting into (7) the expressions given by Equations (3) and (6), and taking into account Equation (5), it follows:
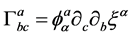 (8)
(8)
In spite of the fact that Equation (8) may look similar to the Weitzenbock connection for a manifold with curvature and torsion, due to the symmetry of the connection, it corresponds to a torsion-free manifold.
By substituting into the usual definition of the Riemann curvature the above expression for the affine connection one gets:

and after some straight forward algebraic transformations, making explicit use of the fact that the affine connection is symmetric, we obtain the following expressions for the Riemann and Ricci tensors for a torsion-free curved manifold:


where it was written

with the following properties:




Taking into account that

we can re-write (11) as:

and taking into account Equation (16) we finally obtain:

Equation (19) is the usual Ricci tensor of GR for a torsion-free curved manifold using the parametric representation of the metric tensor.
3. The Self-Interacting Abelian Gauge Theory
Let us consider a set of vectors 



As before, the matrix 

Next, it is required that the equations for 



As a consequence of Equation (12) 
To guarantee the symmetry of the equations one has to introduce a covariant derivative. The standard procedure in normal Yang and Mills theory is to introduce an auxiliary field, the gauge potential








In this form, the gauge potential itself belongs to the group of symmetry. It follows from (16) that 

Equations (24) and (25) define the covariant derivatives of a self-interacting abelian gauge field. The covariant derivatives can also be written as:

As a consequence of (16), the first term on the right hand side in Equation (26) vanishes so that:

Similarly,

and, since 

For a given vector

and conversely,

where 

Under a gauge transformation


and the covariant derivatives are given by:

and

These equations, when applied to 

The idea of self-interacting gauge field can be extended to non-abelian symmetries; nevertheless, the discussion will be restricted here to the abelian case due to its relevance to gravity.
As is the case in any Yang and Mills theory, the commutator of covariant derivatives is proportional to the gauge field
To compute the commutator we first calculate
from which we obtain:

Similarly,

Finally,

For the special cases in which

Further,

is analogous to Einstein’s equation for the gravitational field. Here κ is the coupling constant and 


It must be emphasized that Equation (38) was derived without any reference to the dynamics of curved space-time. Thus, in this theory space-time can be considered to be a fixed background.
The fact that Equation (39) for the gauge field is identical to the equations of GR implies that the corresponding solutions are the same, thus, for example Schwarzschild solution or the cosmological solutions of GR can correspondingly be looked upon as gauge fields in flat space-time.
4. Conclusion
It has been proved in this work that the equations of an abelian self-interacting gauge field are identical to the parametric form of Einstein’s equations of classical GR for a torsion-free curved space. Therefore, the classical theory of gravity can be describe either by the usual theory of general relativity, based on the dynamics of curved space-time, or, alternatively, as a non-linear self interacting gauge theory. This allows formulating the theory of the gravitational field on an equal footing with the other theories of the fundamental interactions of matter, based on the same general principle: gauge symmetry.
Acknowledgements
The author would like to express his gratitude to the late Samuel Schiminovich for many enlightening discussions.
Cite this paper
Wisnivesky, D. (2017) General Relativity and the Theory of a Self-Interacting Abelian Gauge Field. Jour- nal of Modern Physics, 8, 1152-1157. https://doi.org/10.4236/jmp.2017.88076
References
- 1. Schrödinger, E. (1950) Space-Time Structure. Cambridge University Press, Cambridge, p. 112.
- 2. Palatini, A. (1919) Rendiconti del Circolo Matematico di Palermo, 43, 203-212.
https://doi.org/10.1007/BF03014670 - 3. Weinberg, S. (1972) Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley & Sons, New York, 365-373.
- 4. Ashtekar, A. (1986) Physical Review Letters, 57, 2244-2247.
- 5. Ashtekar, A. (1987) Physical Review D, 36, 1587-602.
- 6. Rovelli, C. (1991) Classical and Quantum Gravity, 8, 1613-1675.
- 7. Arnowitt, R., Deser, S. and Misner, C.W. (1962) Gravitation: An Introduction to Current Research. John Wiley & Sons, Inc., New York, 227-265.
- 8. Clifton, T., Ferreira, P.G., Padilla, A., et al. (2012) Physics Reports-Review Section of Physics Letters, 513 Edic 1-3, 1-189.
- 9. Eddington, A.S. (1952) The Mathematical Theory of Relativity. Cambridge University Press, Cambridge, p. 149.


