Journal of Modern Physics
Vol.08 No.03(2017), Article ID:74439,8 pages
10.4236/jmp.2017.83022
Spacetime Geometry and the Laws of Physics
D. M. Kalassa
Gatineau, Québec, Canada

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 13, 2017; Accepted: February 25, 2017; Published: February 28, 2017
ABSTRACT
The Laws of Classical and Quantum Mechanics are well known. However, their origin remains mysterious and their interpretation controversial. It has been argued that this situation will continue until one manages to derive the Laws of Physics from some very first principles. In this paper, we use basic concepts of Differential Geometry to yield the Klein-Gordon equation and the Lagrange equations of Relativistic Mechanics without using the standard postulates of Quantum Mechanics, Special Relativity or even General Relativity.
Keywords:
Scalar Field, Curved Spacetime, Klein-Gordon Equation, Relativistic Trajectories, Charged Particles

1. Introduction
Quantum Mechanics plays an important role in Science and Technology today. Its predictions have been always confirmed and steadily improved. Applying its calculation rules, we can compute the properties of matter to very high accuracy. However, its foundations remain obscure. There have been several attempts to derive the Schrödinger equation from very different principles including two published derivations by E. Schrödinger himself [1] [2] , the analogy to Classical Electrodynamics [3] [4] , Stochastic models [5] [6] , uncertain relations [7] , just to name a few, but none has been universally accepted. Using a so powerful theory like Quantum Mechanics without understanding its rational is somewhat frustrating for scientists. Therefore many interpretations of Quantum Mechanics have been developed in the course of time leading to endless debates, see e.g. [8] and references therein.
Discovering the origin of the Klein-Gordon equation is an important step to solve the mysteries behind the laws of Physics, since it is a bit more than just an equation for spin-zero particles. It can be related to the Dirac equation and to some extent to higher spin theories as well as to the non-relativistic Schrödinger equation. Quantum Mechanics occupies a very unusual place among physical theories: it contains Classical Mechanics as a limiting case, yet it requires this limiting case for its own formulation (p. 3 in [9] ). This is in our view a clear hint towards a close relation between the two theories. Several derivations or interpretations of Quantum Mechanics start with the textbook axioms of Quantum Physics, but this is nonsense according to some authors [8] [10] . The results of this paper should help answer questions raised by the unexpected coexistence of Classical and Quantum Mechanics in some macroscopic topological insulators [11] .
In Section 2, we derive the Klein-Gordon equation for free fields in a curved space time from purely geometrical considerations. In Section 3, we introduce interactions of the scalar field with some vector potentials. In Section 4, we discuss our results and in Section 5 we give our conclusions.
2. Free Scalar Fields
The idea that the laws of Classical Mechanics may have a geometric origin is indeed very old. One may e.g. cite Lagrange (1736-1813) [12] :
Nous allons employer la théorie des fonctions dans la mécanique. Ici les fonctions se rapportent essentiellement au temps, que nous designerons par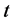 ; et comme la position d’un point dans l’espace dépend de trois coordonnées rectangulaires
; et comme la position d’un point dans l’espace dépend de trois coordonnées rectangulaires ,
,  ,
, 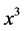 , ces coordonnées, dans les problèmes de mécanique, seront censées être fonctions de
, ces coordonnées, dans les problèmes de mécanique, seront censées être fonctions de . Ainsi on peut regarder la mécanique à quatre dimensions, et l’analyse mécanique comme une extension de l’analyse géométrique.
. Ainsi on peut regarder la mécanique à quatre dimensions, et l’analyse mécanique comme une extension de l’analyse géométrique.
This program has been fulfilled to some extent with the advent of Special Relativity and Generality. However it is not clear whether this picture should be extended to Quantum Mechanics. This is the aim of the present study.
First of all we assume that spacetime is a smooth four dimensional real Riemann manifold. Each spacetime point  is labeled by four coordinates
is labeled by four coordinates
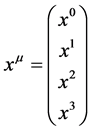 (1)
(1)
where 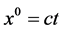 represents the time coordinate and
represents the time coordinate and 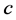 is a dimensional constant (e.g. the velocity of light in empty space),
is a dimensional constant (e.g. the velocity of light in empty space), 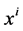 are spatial coordinates
are spatial coordinates
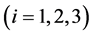 . The points of a curve are characterized by their distance
. The points of a curve are characterized by their distance  from the origin.
from the origin. 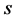 is defined as
is defined as
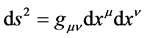 (2)
(2)
where  is the metric tensor. It can be used to evaluate scalar products and to rise as well as to lower the indices of four dimensional vectors. One defines to this purpose the inverse tensor
is the metric tensor. It can be used to evaluate scalar products and to rise as well as to lower the indices of four dimensional vectors. One defines to this purpose the inverse tensor 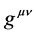 by the the relation
by the the relation
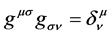 (3)
(3)
where 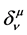 is the Kronecker delta symbol. It takes the value one for equal indices and zero otherwise. To obtain a real value of the curve length
is the Kronecker delta symbol. It takes the value one for equal indices and zero otherwise. To obtain a real value of the curve length 

Instead of 


The velocity vector along the curve is defined as

It yields by definition (2) the identity

where

We are now ready to study the variation of scalar field 

The total derivative of the scalar field 

where 

We use implicitly Einstein’s sum convention [13] .
Since 


where 


Equation (9) yields

The expression 



where 









Equations (6) (7) (14) yield


Equations (11) and (16) mean that the scalar field 

for free particles if 

To show (17) multiply Equation (16) with 





One may try to use the left hand side of (19) as a Lagrangian density

for the Klein-Gordon field. The action reads

where

It leads to the Klein Gordon equation

in curved space times. Very often some extra terms containing the curvature scalar 
Unlike the usual derivations of Quantum Mechanics the geometrical path taken in this paper is inconsistent unless we give an equation for the classical trajectory as well. To do this recall that Equation (14) looks like Hamilton’s equation

for which we already know the Hamiltonian

and we determine the Lagrangian

It yields the Euler-Lagrange equations

where

are Christoffel symbols [13] . They vanish in Minkowski space. Equation (26) may also be written without indices as

This is a geodesic equation. It means that the curve 
Finally it is interesting to solve Equation (13). We find

only the phase of the wave function 



Equations (11) (14) (27) determine a set of lines (trajectories) that do not intersect and that are characterized by a probability which is the same at each of their points. This is clearly an addition to the standard interpretation of Quantum Mechanics.
3. Interactions
The simplest way to insert interactions of the Klein-Gordon field with external fields is given by the principle of minimal substitution:

which means

and

we define the Lagrangian density for the Klein-Gordon equation

and the action

It yields Lagrange’s equations in Minkowski space (18)

and

in more general spacetimes.
The Hamiltonian for the classical trajectory is

The Lagrangian reads

It yields the Euler-Lagrange equations

where

is Maxwell’s field strength tensor. Equation (40) is postulated within Special Relativity and General Relativity as a generalization of Newton’s second law for the motion of a particle in the electromagnetic field

Adding an arbitrary phase 

in full agreement with gauge theory.
4. Discussion
It is generally accepted that Classical Mechanics is the limit of Schrödinger equation when



Requiring the velocity 

Trajectories have always been related to particles. They have been banned from Quantum Mechanics but we find here that they are intrinsic properties of the fields (wave functions) themselves. It means that Quantum Mechanics in its present status may indeed be somehow incomplete and we need to correct this. New interpretations of Quantum Mechanics and the uncertainty relations are therefore required.
There are some claims of observed macroscopic quantum effects e.g. topological insulators which exhibit a coexistence of Classical and Quantum Mechanics, in contradiction with textbook knowledge [11] . Our analysis shows however that Classical and Quantum Mechanics have the same mathematical origin. They are completely tied and It seems reasonable to expect that both should be valid all over the universe with practical limitations given by Heisenberg uncertainty relations and the experimental facilities. This is matter of further research.
5. Conclusion and Outlook
We have shown how the Klein-Gordon equations of Quantum Mechanics and relativistic Newton’s equations of Classical Physics can be simultaneously derived from the mathematical properties of scalar functions and not from physical principles and postulates. Since fermions obey the Dirac equation but also the Klein Gordon equation in Minkowski space, we may see why they behave just like other particles (bosons) in Classical Physics. We wish the same could happen in curved spacetimes [15] [16] , but this remains to be confirmed. There are big questions about particles: how do they inherit their properties (rest mass, energy-momentum, electric charge, classical trajectories etc.) from fields? Understanding the Mathematics behind the laws of Physics is not only thrilling but it is required in order to achieve a deeper understanding of nature. Geometry (Gravity) seems to play a decisive role in the selection of the fundamental laws of Physics.
Cite this paper
Kalassa, D.M. (2017) Spacetime Geometry and the Laws of Physics. Journal of Modern Physics, 8, 330-337. https://doi.org/10.4236/jmp.2017.83022
References
- 1. Schroedinger, E. (1926) Annals of Physics, 79, 361-376.
https://doi.org/10.1002/andp.19263840404 - 2. Schroedinger, E. (1926) Annals of Physics, 79, 489-527.
https://doi.org/10.1002/andp.19263840602 - 3. Ward, D. and Volkmer, S. (2006) How to Derive the Schroedinger Equation.
arXiv:physics/0610121 - 4. Field, J.H. (2004) European Journal of Physics, 25, 385-397.
https://doi.org/10.1088/0143-0807/25/3/006 - 5. Nelson, E. (1966) Physical Review, 150, 1079-1085.
https://doi.org/10.1103/PhysRev.150.1079 - 6. Davidson, M.P. (1979) Journal of Mathematical Physics, 20, 1865-1869.
https://doi.org/10.1063/1.524304 - 7. Hall, M.J.W. and Reginato, M. (2002) Journal of Physics A, 35, 3239-3303.
https://doi.org/10.1088/0305-4470/35/14/310 - 8. Fuchs, C.A. (2003) Journal of Modern Optics, 50, 987-1023.
https://doi.org/10.1080/09500340308234548 - 9. Landau, L.D. and Lifschitz, E.M. (1977) Quantum Mechanics: Non-Relativistic Theory. 3rd Edition, Volume 3, Butterworth-Heinemann, Oxford.
- 10. Rovelli, C. (1996) International Journal of Theoretical Physics, 35, 1637-1678.
https://doi.org/10.1007/BF02302261 - 11. Wu, L., Salehi, M., Koirala, N., Moon, J., and Armittage, N.P. (2016) Science, 354, 1124-1127.
https://doi.org/10.1126/science.aaf5541 - 12. Enriques, F. (1911) Encyclopedie des Sciences Math. Tome 3. 1-71.
- 13. Schutz, B.F. (1990) A First Course in General Relativity. Cambridge University Press, Cambridge.
- 14. Sjostrom, D.-M. (2013) Bosons and Fermions in Curved Spacetimes. PhD Thesis, Norvegian University of Science and Technology, Mai.
- 15. Arminjon, M. (2008) Foundations of Physics, 38, 1020-1045.
https://doi.org/10.1007/s10701-008-9249-6 - 16. Arminjon, M. (2010) Brazilian Journal of Physics, 40, 242-255.
https://doi.org/10.1590/S0103-97332010000200020

