ABSTRACT

We generalize relativistic quantum mechanics and the Standard Model of elementary particle physics by considering a finite limit for the smallest measurable length. The resulting theory of Space-Time Quantization is logically consistent and accounts for all possible particle states by means of four new quantum numbers. They specify possible variations of wave functions at the smallest possible scale in space and time, while states of motion are defined by their large-scale variations. This theory also provides insight into the nature and properties of dark matter particles. It can facilitate their detection and identification because of a very strict conservation law.

Keywords:

Dark Matter, Elementary Particles, Relativistic Quantum Mechanics, Space-Time Quantization

1. Introduction

Although more than 80% of all matter in our universe is dark matter (DM), it has not yet been possible to identify this type of particles. We know only that they cannot interact with electromagnetic fields, but are subjected to gravitational forces. They have thus to be electrically neutral and to carry some mass. To understand the nature and properties of DM particles is “one of the most fundamental open questions in cosmology and particle physics” [1] . It is related to the equally basic problem of identifying the nature of dark energy and the cause of the accelerated expansion of our universe [2] . Moreover, we know that the Standard Model (SM) of elementary particle physics describes very remarkable facts, but does not explain them. This “spectroscopy” is similar to that of atomic physics before the development of quantum mechanics.

All these problems seem to call for a generalization of present day theories, as this happened already when it appeared that classical mechanics contained simplifying assumptions. They were corrected by the theory of relativity and quantum mechanics, but we kept the concept of a “space-time continuum”. This allows us to use differential equations, but physical laws have to be verifiable. They imply thus the belief that it should be possible to measure always smaller and smaller lengths, without ever reaching a finite limit. Where does this conviction come from and are the justifications really compelling?

At the beginning of rational thinking, it was obvious that a length has to be measured by comparing it to a juxtaposition of some invariant unit of length. To achieve utmost precision, it would have to be an extremely small, undividable length. This led to the idea that any length is an integer multiple of some elementary length a. Adjacent sides of a square and the length of its diagonal would then respectively be equal to na and ma, where n and m are integer numbers. Because of the Pythagorean Theorem, we get thus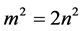, whatever the value of a may be. Since the square of an odd number is odd, it appears that m is an even number. Setting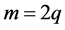, where q is an integer number, it appears that. The number n would thus also be even, but when n and m can be divided by 2, it is not true that a is undividable. It was concluded that the divisibility of lengths has to be unlimited.

This proof was perfectly rational and justified the mathematical concept of “infinitely” small intervals. It had even great cultural impact, since it supported the idea that logical reasoning is able to grasp what is out of reach of observations. It was therefore generally accepted that space is continuous, but this claim was flawed. Indeed, when the smallest measurable length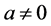, precisely measured lengths of two adjacent sides of a square are both equal to na. However, the length of the diagonal can then be calculated. It does not have to be equal to ma, where m is an integer number.

To distinguish measured values from calculated ones did not seem necessary as long as physical laws were considered as statements about reality, telling us how it is. Today, we know that they are concerned with knowledge that we can get about reality by means of measurements. This is very different for two basic reasons: 1) nature can impose restrictions on our measurements and 2) knowledge can be expressed in very subtle ways. This applies especially to space and time. Newton postulated the existence of an “absolute space” that is motionless and an “absolute time”, flowing always and everywhere in the same way. Space and time were thus assumed to be some kind of substances. These postulates were sufficient to account for a vast domain of observations, but had to be corrected when this domain was enlarged.

There are also electromagnetic phenomena. Einstein realized that they require that the velocity c of light in vacuum has to be independent of the chosen reference frame. This was incompatible with the Galilean velocity addition law and with Newton’s concept of space and time. Einstein solved this conflict, by considering that space and time are only defined by possible results of measurements. Nature could thus impose that measurements of lengths and durations have to yield the same value c, when the velocity of light in vacuum is measured with respect to inertial reference frames. Because of the principle of relativity, Newton’s laws of motion had then to be modified for very great velocities.

Planck discovered another universal constant. Its value h defines the smallest energy quantum hν for light waves of frequency ν, but it is also the quantum of action. It determines thus the smallest possible value of a specific combination of space-time coordinates and kinematical observables. This led to “quantization rules” for possible states of motion of very light material particles, but these rules could only be explained by introducing the concept of wave functions. They can store an enormous amount of information, because of their possible variations in space and time. Relativistic Quantum Mechanics (RQM) accounts even for annihilation and creation processes, but something is missing. RQM provides no information about possible types of elementary particles that can be transformed into one another.

Why are wave functions (for one particle) and fields (for any number of identical particles) unable to store this information? Could this be due to the postulate that space and time are continuous? Is it a logical necessity or not? To answer this question, we considered that Nature could impose another restriction and constructed a theory of Space-Time Quantization (STQ) that generalized RQM to account for c, h and a. This is the value of the smallest measurable length, which is not yet known, but it would be sufficient to show that 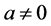leads to logical inconsistencies, to prove that space and time are continuous. Actually, it was necessary to replace differential equations by finite-difference equations. This led to modifications for very rapidly varying 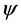functions, but not to logical inconsistencies. The existence of a quantum of length 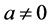cannot be excluded.

Could this be relevant for elementary particle physics? We were surprised to discover that variations of 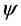functions in space and time can be described in a more detailed way when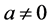. At the smallest possible scale, it is even necessary to introduce four new quantum numbers. It appeared then also that they allow us to distinguish elementary particles from one another [3] [4] . Even their possible transformations can be specified. The agreement with a huge amount of very remarkable empirical data, accumulated during more than half a century, means that STQ is real.

Nevertheless, the concept of a space-time continuum is so deeply rooted in our culture, that it is natural to resist any change in this regard. It has been objected, for instance, that the existence of a finite quantum of length is forbidden by the Lorentz transformation for space-time coordinates. It accounts for the constancy of c, but presupposes that space and time are continuous. The constancy of c, h and a for different reference frames is insured by a generalized Lorentz transformation.

Another objection can result from the usual, intuitive concept of motions. It is based on the fact that there are continually existing material objects. Their center of mass can thus only move from a point A to another point B by passing through a continuous array of intermediate points. This would also be true for any point-like material particle in non-relativistic quantum mechanics, but how do we define knowledge in regard to motions? Quantum mechanics accepts that space-time coordinates can be measured with absolute precision, but it is sufficient to know the probability distribution for possible results, to calculate the average position of a point-like particle at any particular instant. Even when measurable positions are quantized in a given reference frame, the calculated average position does not have to coincide with one of these values. STQ is thus compatible with continuous motions.

It has also been stated that the Planck length is the smallest measurable distance. Planck wanted only to attract attention on the fact that h, c and the gravitational constant G yield a system of units of universal validity. The Planck length is a natural unit for quantum gravity, like the Bohr radius in atomic physics, but the concept of a quantum of length is more general. To claim a priori that it has to be equal to the Planck length would be arbitrary, like the assumption that.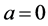

String theories try to account for the degrees of freedom of elementary particle physics by assuming the existence of additional dimensions of space. They would not be observable, if they were wrapped up like the surfaces of extremely thin filaments, which can vibrate. This ingenious paradigm remains compatible with the usual concept of a space-time continuum, but STQ explains elementary particle physics in a simpler way. The normal 4-D space-time is sufficient when.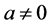

The organization of this article is the following. In Section 2, the construction of the theory of STQ is briefly reviewed and justified in regard to possible states of motion. In Section 3, we generalize this theory to account also for particle states. The aim is to present the proposed theory in a compact, unified and more complete way. In Section 4, we show that STQ explains and generalizes the Standard Model of elementary particle physics. This accounts also for the nature and properties of DM particles. In Section 5, we indicate how their detection and identification can be facilitated by a very strict and general conservation law. Section 6 presents conclusions and points towards further applications.

2. Space-Time Quantization

2.1. The Generalized Energy-Momentum Relation

The quantum-mechanical description of motions is much more detailed than the classical one, but we are still speaking of the momentum p and energy E of a particle, although these observables acquired a radically new meaning. When their values are exactly known for any free particle that is moving along the x-axis of a given inertial frame, we express this knowledge by means of the wave function

(1)

where and 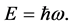The amplitude A is constant and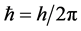. The classically defined values of E and p were related to one another by means of Einstein’s relation, where 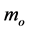is the rest mass:

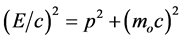(2)

Relativistic Quantum Mechanics (RQM) postulated that this relation remains true, although it does not include h. Louis de Broglie discovered, indeed, that the wave-par- ticle duality can be generalized without modifying (2). Actually, he defined the new observables 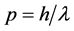and. Their values are only determined with absolute precision when the function varies always and everywhere with the same wavelength and the same frequency. This is an idealization, but it is sufficient that results from a linear superposition of harmonic functions like (1) to get a wave-packet. The values of p and E are then not exactly known, but their average values are still related to one another by (2). We can even define local values and at any particular point in space and time. They depend only on the variations of at the smallest possible scale around this point. They should there be the same as if p and E were exactly known. The usual concept of a space-time continuum implies therefore that

(3)

and designate partial derivatives of with respect to x and t. For any precisely defined state of motion (1), we get thus and. It is customary to speak of operators, but their physical meaning is more important than formal rules. Actually, we define new observables and RQM postulates that and have also to satisfy (2). This yields the Gordon-Klein equation, which is a second-order differential equation. However, when, we have to adopt the definition

(4)

For an exactly known value of p, it follows from (1) that is equivalent to setting

(5)

In general, the local value depends not only on, but also on the quantum of length a. The instantaneous value of is defined in the same way, by considering the second order finite derivative of with respect to ct. The Gordon- Klein equation has thus to be replaced by a finite difference equation. It is equivalent to replacing Einstein’s relation (2) by the generalized energy-momentum relation

(6)

This is a new physical law, since it differs from (2) when. All possible states of motion of any free particle are specified in any given inertial frame in terms of p and E. These values are subjected to the condition that. It is reduced to Einstein’s relation (2) when space and time are continuous () or when, but extremely small. For usual values of E and p, it is then possible to approximate the sine-functions by their arguments. The essential difference between (2) and (6) is therefore that Einstein’s relation was assumed to be valid for arbitrarily high energies, while the generalized energy-momentum relation implies that the arguments of the sine-functions are limited by. Because of the de Broglie relations and, this means that we can only consider wavelengths and frequencies. It would be meaningless to consider oscillations of at smaller scales than measurable ones. They can be imagined, but are physically irrelevant.

It appears thus that and when. The rest energy is. The curves resulting from (6) coincide thus with Einstein’s hyperbolas (2) for usual values of E and p. However, they shrink when. This can be graphically shown [4] , but we can immediately deduce from (6) that when the rest-energy, there remains only one possible state: p = 0 and E = E_o. In quantum mechanics, absolute rest means that the function has everywhere the same value (λ = ∞). It follows that is the total energy content of our universe. Indeed, if a material body did have such a high rest energy, there would be no energy left that could appear in the form of kinetic energy. The actual value of is unknown, but energies cannot be infinite when. What would happen for motions at extremely high energies?

Quantum mechanics describes the average motion of any particle by considering a wave-packet. It results from a superposition of harmonic functions like (1), where. The group velocity is then. Since Einstein’s relation (2) remains valid in RQM, the velocity even for arbitrarily high energies E. However, according to (6), the slope of the curves is greater than c for extremely high energies [4] . It is important in regard to principles that superluminal velocities are not excluded when, but this allows us also to test the logical consistency of STQ.

2.2. The Generalized Lorentz Transformation

The principle of relativity requires that all physical laws are independent of the chosen reference frame. The same state of motion is thus defined for a given free particle by in one inertial frame and by in another one. The correspondence results from the invariance of (6). It can be expressed by considering local values for the momentum and energy variables or sine-functions of E and p. The resulting “generalized Lorentz transformation” accounts for constant values of c, h and a, but the derivatives and yield a generalized velocity addition law. The relative velocity of the reference frames has to be defined in terms of the average velocity of a material object that is at rest in one frame. In the other frame, it could move at superluminal velocities.

The principle of causality requires that the sequence of events is the same for any observer, since causes have to precede their effects for any observer. So-called “tachyons” are hypothetical particles, assumed to obey (2) with an imaginary rest mass [5] . They can thus only move at superluminal velocities, but the invariance of (2) would impose the usual Lorentz transformation. For superluminal velocities, it contradicts the principle of causality. We verified that the generalized Lorentz transformation does not violate this principle [6] . It justifies even Mach’s principle, requiring that inertial frames should be related to the whole universe.

3. Foundation of Elementary Particle Physics

3.1. New Quantum Numbers and Particle States

Since the possibility of STQ is not excluded, we wanted to know if this could be related to elementary particle physics. Actually, it appeared that functions are able to store more information than we thought. To see why this is possible, we consider ideally precise measurements of the coordinate x along an arbitrarily chosen reference axis. When “x” is a possible result, “−x” is also one, since the orientation of the x-axis could be reversed. However, the distance 2x has to be an integer multiple of a. It can be an even or odd number. Thus,

(7)

There are two lattices of lattice-constant a. The first one will be called the “normal lattice”, since we are accustomed to the idea that x should be measured by starting at the chosen origin. There is also an “intercalated lattice” and the wave function of any point-like particle has to be defined for all possible values of x. The probability

distribution cannot allow for any ambiguity. It has to be single valued and to

be compatible with a smooth variation for the continuum approximation (). Nevertheless, there is a degree of freedom, since can be positive or negative on the intercalated lattice with respect to its values on the normal lattice (Figure 1(a)). There are even more than two possibilities, since is a complex function. It can be modulated by a sign-function, to differentiate anywhere on the intercalated lattice with respect to on the normal lattice (Figure 1(b)). This allows for when and

These considerations apply also to for any reference frame. It is only necessary that the three spatial axes are not coplanar to allow for independent measurements. The time-axis is freely chosen. We get thus four quantum numbers, which can be positive or negative integer numbers. Every set of u- quantum numbers defines a possible “particle state”. They can be specified by imaging 4 panels with pointer needles that can only be rotated by half-turns towards the left or the right. We can also define particle states by vectors in the 4-D space of u-quantum numbers. The homogeneity and isotropy of space implies that the u-quantum numbers are always and everywhere identical in the whole universe for a given type of particles. They are even identical for any, arbitrarily chosen reference frame, because of the principle of relativity. Inertial frames are only necessary to define states of motion of free particles by means of the energy-momentum relations (2) or (6).

Actually, we are expressing knowledge concerning “particles states” by means of possible variations of functions at the smallest possible scale in space and time. Quantum mechanics defined “states of motion” by means of large-scale variations of functions, specified in terms of possible wavelengths and frequencies. Since large- scale and small-scale variations can be combined by multiplexing, much more knowledge can be stored in functions than allowed by a space-time continuum.

3.2. The Generalized Dirac Equation

We discovered the new degrees of freedom by applying Dirac’s procedure. He replaced the Gordon-Klein equation by an equivalent set of first-order differential equations. Since we believed that space-time coordinates have to be measured by starting at the

origin of the chosen frame, we defined first-order finite derivatives in terms of and. However, because of (7), the local value of the momentum p along the x-axis can be defined in a unique and more precise way when

When the momentum p is well defined, it follows from (1) that

(8)

This result is similar to (5), but accounts also for the sign-function. The concept of a space-time continuum () led to (3), but this concealed the existence of additional degreees of freedom. Even (4) did only account for states of motion, while (8) depends also on possible particle states. For usual states of motion, where the energy, we get Einstein’s relation (2), but for local values like (8). It has to be replaced by the generalized Dirac equation

(9)

Dirac’s equation was equivalent to setting the four sign functions equal to 1. That was sufficient to discover already 4 possible states, since the matrices and yield four coupled relations. Considering electrons, Dirac knew that their spin has two possible orientations along any given z-axis. He attributed the two other possibilities to the fact that Einstein’s relation (2) allows for positive and negative energies. The curves would be hyperbolas, indeed. They allow for and, but if negative energy states were possible for electrons, these particles would be unstable, which is unacceptable.

To eliminate transitions towards negative energy states, Dirac took into account the fact that electrons are fermions. They have to occupy different energy states. Thus, he assumed the existence of an infinite number of electrons, occupying all possible negative energy states. This “Dirac Sea” would produce no observable effects, unless an electron is excited from a negative energy state to a positive energy state. The resulting “hole” would behave like a particle of rest-mass m_o, but its charge is +e instead of −e. Dirac predicted therefore that a photon could create an electron-positron pair. This was experimentally confirmed and provided the first example of particle-antiparticle pairs. Dirac’s assumption that can be positive or negative was equivalent to setting in (9). However, there are much more possibilities, although free particles can only have positive energies.

3.3. Symmetries and Conservation Laws

Any symmetry results from modifications that yield related images. According to STQ, particle states are defined by means of u-quantum numbers, which can be positive or negative. Any vector in the 4-D space of u-quantum numbers has thus an image, repre- sented by the opposite vector. It defines another particle state, but the rest masses are identical. They depend on the cloud of virtual particles that can be created and absorbed by a given particle and thus on all its u-quantum numbers. This yields the particle-antiparticle symmetry

(10)

Figure 1(b) shows that by inversing the orientation of the x-axis, we change the sign of. Since the parity operator P reverses the orientation of all spatial axes, it changes the sign of, and. The operator for time reversal changes only the sign of, but the combined operator converts any particle into its antiparticle. Modulation of functions at the smallest possible scale in space and time reminds us of the distinction between acoustical and optical phonons in ionic crystals, but functions require no material medium. They are tools for expressing knowledge. Although elementary particles are entities that carry energy and momentum, electric charge and other attributes, they can also be viewed as possible “excitations of space and time”.

States of motion and particle states are respectively defined by large-scale and small scale variations of functions in space and time. Although the spin may seem to be an intrinsic property of particles, it is defined by large-scale variations of their function. Indeed, when the generalized angular momentum component along a given z-axis is precisely known, the function varies around this axis like, where is the azimuthal angle with respect to this axis. The pro- bability distribution has to be single-valued, but this allows for. Thus, m can be an integer or half-integer number and the ensemble of all possible elementary particles is divided in two classes: bosons and fermions. This distinction is independent of possible modulations of at the smallest possible scale in space and time. For every particle state of a fermion, there is a particle state for a boson that is characterized by the same set of u-quantum numbers and vice-versa. Representing fermion states by round brackets and boson states by square brackets, this means that

(11)

This correspondence defines supersymmetry (SUSY), but does not require that supersymmetric images have the same mass. STQ yields also information about possible transformations of elementary particles. Usually, one particle is annihilated by creating two different particles or vice-versa. Since the functions of particles that coexist in the initial or final state are multiplied by one another, their phase factors are then added, but the result has to be identical for the initial and final state. This yields the well-known conservation laws for the energy and momentum variables. They are compatible with the energy-momentum relation (2) or (6) for two successive transformations, since the intermediate state is then subjected to Heisenberg’s uncertainty relations. They result from the fact that the phase factor of (1) contains products like px and Et. However, the sign-functions depend only on u-quantum numbers. We get thus a very strict conservation law for the sum of u-quantum numbers before and after any transitions between particle states. The sum of u-quantum numbers has to be identical for the initial and final states, separately for every space-time axis. This is equivalent to a vector addition law in the four-dimensional space of u-quantum numbers, as well for as for states. This allows for

Photons are in the state and can be annihilated by creating a particle- antiparticle pair, but a particle and its antiparticle can also annihilate one another to create a photon. If the Big Bang did create particles and antiparticles in equal proportions, they would have annihilated one another. The observed cosmic matter-antimat- ter asymmetry raises thus a fundamental problem. It can be solved [7] , but we will now simply accept that the Big Bang created only those fermions that we call “particles”. Electrons and quarks are particles, for instance.

The conservation law allows also for. This accounts for the emission and absorption of photons, but it is well-known that these processes are only possible for electrically charged particles. Since electromagnetic waves correspond to vector fields, they are coupled with possible variations of functions along the three spatial axes. The electric charge of a particle has thus to depend on, but permutations of these quantum numbers should be irrelevant, since the spatial reference axes can be chosen in a completely arbitrary way. This yields a symmetry or kinship between particles that have the same electric charge Q, defined in units e by the average value of the spatial u-quantum numbers:

(12)

4. The Generalized Standard Model

4.1. Elementary Fermions and DM Particles

The first generation of the Standard Model (SM) corresponds to spin fermions, characterized by the triplet, where these quantum numbers can be equal to 0, , while. For orthogonal, and axes, this yields the cubic lattice of Figure 2. Every lattice-point corresponds to a different particle state. The positron

corresponds to the state and the electron to. The elec- tron-neutrino and its antiparticle are both in states. All known leptons are thus represented by points that belong to the axis. Quarks correspond to the vertices of the red triangles. There are three possible states for up-quarks (u), since they are of type with 3 possible permutations, while. Down-quarks (d) allow for 3 states of type and. Antiparticle states are defined by (10) and represented by opposite points with respect to the center. Antiquarks have thus also 3 possible states, represented by the vertices of the green triangles.

Since DM particles are electrically neutral and were not produced by accelerators, they could not be included in the SM. However, the vertices of the yellow hexagon correspond to states of type with 6 possible permutations. The charge Q = 0. We add two states, represented by superposed points at the center of the hexagon. They differ from the states for and, since they belong to the hexagon, although they are also situated on the axis. These states correspond to elementary DM particles, but this octet is constituted of 4 particles and 4 antiparticles.

By analyzing empirical results it was possible to distinguish 3 generations of elementary particles. They result from. These generations display the same family structure, including always two types of quarks that have 3 possible states. They were said to be red (R), green (G) and blue (B) color states. The SM could not explain why there are 3 generations and 3 color states [8] , but STQ reveals that the 3 color states result from the fact that space is three-dimensional and that different generations are associated with the time variable.

When Figure 2 is viewed along the Q axis, the triangles and the hexagon yield Figure 3. The color code for quarks is chosen to be similar to the repartition of R, G and B colors in the color plane of colorimetry. The superposed triangles for u-quarks and d- quarks yield superposed color states when we adopt the following convention:

for

for

Antiquarks are said to have anticolors. The antired state corresponds thus to for the antiquark and to for the antiquark. The 8 possible states of elementary DM particles are represented in Figure 2 by points that belong

to the plane Q = 0. Since it is perpendicular to the Q-axis, like the planes for quarks, they can be considered as defining “neutral quarks”. For simplicity, we called them narks [3] [4] . They are the supersymmetric partners of gluons. The existence of gluons was deduced from empirical results, indicating that a quark can change its color by creating a gluon. According to usual conventions,. Because of the conservation law for u-quantum numbers, this means that for a u-quark and for a d-quark. We have thus to attri- bute the color to the state of gluons. We adopt the same color code for narks, to get superposed color states in Figure 3.

We distinguish narks from antinarks, since these fermions were already created dur- ing the Big Bang. They are thus subjected to the cosmic matter-antimatter asymmetry. This can be explained, since quarks created gluons, which could be transformed into narks. Thus, for instance. This allows us to adopt the following color code:

for states (narks)

for states (antinarks)

Possible color states for narks and antinarks are represented by opposite points in Figure 3, but they are situated in the same plane Q = 0. There are also two states for narks and antinarks. They are “color-neutral” and represented by two superposed point at the center of the hexagon.

Symmetry considerations are very useful to analyze incomplete empirical data, since they can reveal “empty places” that might be filled later on. This happened for Mendeleyev’s table of chemical elements, which could only be explained by quantum mechanics. Gluons are bosons that were essential ingredients of the SM. It has thus been suggested that supersymmetric partners of gluons might also exist. These fermions were called “gluinos”, but considered as purely hypothetical entities. STQ justifies their existence in a direct way and we relate them to DM. The octet of possible states for gluons corresponds to an octet of possible states for elementary DM particles, but for bosons, no distinction is made between particles and antiparticles. It should be noted that we consider gluons and narks as single elementary particles, although they are defined by a color and an anticolor.

4.2. Other Generations and Excited States

The SM considers 3 generations of spin fermions. They are due to. We considered narks for the first generation of the SM in Figure 2, since we have also to expect the existence of and narks, according to the correspondence

There are thus quarks of different “flavor” (u, d, c, s, t and b). All these states are represented by superposed vertices of red triangles with the color code of Figure 3. The orientation of the axis was chosen by setting for the electron. We are thus also free to choose the orientation of the u_ct-axis, so that for the second generation [4] . STQ generalizes the SM not only because of the hexagon in Figure 2. Since is also possible, there are more than 3 generations, although the rest-energy of these quarks and narks may be too high for their production by means of existing accelerators. Even the Big Bang did eventually produce only quarks and narks of the first generation.

We can also consider particle states that correspond to the upper left and lower right vertices of the front side of the large cube in Figure 2. Combining them with the lower rear left vertex of this cube, we get a large triangle. Its vertices define states of type with 3 possible permutations. The electric charge. They can be considered as the first excited states of d quarks, since they imply more modulations of functions on intercalated lattices with respect to the normal one. The first excited states of u quarks are of type. They allow also for 3 permutations and. The triangles for the excited states and of and quarks and their antiparticles are represented by means of interruped lines in Figure 4. The color code is the same as for the corresponding quarks.

Even excited states of positrons and electrons are possible. For the electron, they are of type with 6 possible permutations and. For the positron, they are of type. They are thus colored leptons and represented by points that are situated at the vertices of superposed hexagons in Figure 3. However, in Figure 2 these hexagons would be situated in the planes and be centered on the Q axis. Since electrons and positrons are light particles, we have to expect that their excited states are created more easily than those of quarks and antiquarks.

4.3. Bosons and Possible Interactions

We mentioned that narks are supersymmetric partners of gluons (g), but (11) is more general. The first generation of spin fermions corresponds thus to an ensemble of spin 1 bosons:

(13)

Electromagnetic interactions result from exchanging photons (γ), while weak interactions require exchanges of Z or W^± bosons. Photons and Z particles are in states, but the rest-mass of photons is zero, while Z and W^± bosons are heavy and lead to short-range forces. Weak interactions allow for transformations like, immediately followed by to account for energy and momentum con- servation. Every one of these transformations satisfies the conservation law for u- quantum numbers, since and.

Weak interactions can thus be mentally represented by transitions that are paral- lel to the axis in Figure 2. Since strong interactions result from exchanges of gluons, they imply transitions that are perpendicular to the axis. For instance,. This applies also to transitions inside the plane Q = 0. For instance, or. In short, one vertex of the hexagon in Figure 3 can be replaced by two neighboring ones, but narks are then converted into antinarks and vice-versa. Quantum chromo dynamics (QCD) applies thus also to DM particles.

It is even possible to get transitions between different generations, since should be expected for gluons. Transformations of particle states could also corres- pond to oblique transitions with respect to the axis in Figure 2. They would convert quarks into antiquarks of different color and quarks or antiquarks into leptons. STQ accounts directly for bosons of type and, while Grand Unified Theories (GUT) led to the concept of X and Y bosons in a more complicated way [9] . Supersymmetric partners of leptons were called sleptons (). They are usually considered as being hypothetical bosons, but (13) indicates that they are already known for. In addition to spin 1 bosons, there are also spin 0 and spin 2 bosons, corresponding to scalar and tensor fields. There are thus Higgs bosons and gravitons in other states than.

4.4. Hyperons and Composite DM Particles

Hyperons are composed of quarks or antiquarks, which are strongly bound to one another by exchanging gluons. This yields different types of composite particles, repre- sented in Figure 5, where occupied color states are represented by black dots for quarks and by white dots for antiquarks. We can mentally represent an exchange of gluons between quarks or antiquarks by shifting two dots in opposite directions. Neighboring dots can thus be exchanged, but opposite shifts of two dots along parallel lines are sufficient. It is only necessary that every shift occurs within the same Q plane (for normal gluons with u_ct = 0). This applies also to quarks of different flavors (u, d, c, s, t, b), since two associated shifts are then possible in different Q planes.

A proton (uud) requires that the three quarks are in different color states, since they are fermions. We could thus get and at a particular instant. The resulting particle state is and. All composite particles have to be color-neutral, since no spatial reference axis can be privileged for intrinsic properties of these particles. For mesons, this is achieved statistically by means

of all possible gluon exchanges. We include tetraquarks and pentaquarks in Figure 5. The discovery of () and () tetraquarks was puzzling, since they might be viewed as molecular associations of two mesons. Actually, all quarks and antiquarks are equally bound to one another, since dots can be shifted in different Q planes.

The () pentaquark seemed to be so exotic that its very existence was doubted [10] , but it was confirmed [11] . This is justified by the fact that 2 dots can be superposed for quarks of the same color when they belong to different Q-planes. A new type of tetraquark has been discovered [12] . It may be considered as a combination of a strange B meson () and a π meson (), but even 4 quarks could be strongly bound to one another when they are of different flavor. More exotic compound particles could be created by occupying excited states, like those of Figure 4.

Composite DM particles are constituted of narks and/or antinarks, which are strongly bound to one another by exchanging gluons. Since the resulting particles are similar to nucleons, but electrically neutral, we call them “neutralons”. Figure 6 shows various possibilities in terms of occupied states. Narks are represented by black diamond-shaped dots and antinarks by white ones, since their color states are different from those of quarks and antiquarks. Gluon exchanges can still be represented by opposite shifts of two different dots, but a nark is then transformed into an antinark and vice-versa. We represent neutralons by the symbol N_n where n specifies the number of narks or antinarks that are “glued” together. Since narks and antinarks are spin particles, we get bosons when n is even and fermions when n is odd.

The creation of cosmic DM particles was subjected to the general matter-antimatter asymmetry and compound particles have to be color neutral. N₁ is thus only possible for a nark in the state. The N₃ neutralon is composed of 3 narks, but gluon exchanges transform narks into antinarks and vice-versa. N₅ and N₇ neutralons could have been formed by combining N₁ with adequate bosons, but because of gluon exchanges, the central state can also be occupied by an antinark. The N₂ boson is only stable as long as opposite dots are shifted along the contour of the hexagon. When they were shifted towards the center, they are represented by slightly separated diamonds, but the nark and its antinark will annihilate one another. Cosmic DM particles are thus only stable when they are fermions.

4.5. Hybrid Particles

During the Big Bang, quarks and narks interacted with one another by exchanging gluons, but they were still relatively free until they became definitely bound to one another. Eventually, the cosmos was populated with nucleons (composed of quarks) and neutralons (containing only narks). Quarks and narks got separated, since binding results from superposition of functions and quantum-mechanical resonance effects. The deepest negative energy states and strongest bonds will thus be achieved for elementary particles of the same type. However, during the Big Bang, there could also appear hybrid particles. Figure 7 shows a particle that combines a single nark with a quark and an antiquark. Color states like B and did insure color- neutrality, conserved by specific exchanges of gluons. The resulting particle was not sufficiently stable to survive. The cosmic DM gas contains thus no or nearly no hybrid particles. Nevertheless, it is conceivable that H₁ or H₃ hybrid particles could sometimes result from combining a nucleon with N₁ or N₃ DM particles.

4.6. Interactions between DM Particles

Nucleons interact with one another by exchanging π mesons. This accounts for nuclear forces, which allow for scattering and the constitution of nuclei. Neutralons interact also with one another, but they exchange N₂ bosons. This process is represented for a particular case by the Feynman graph of Figure 8. A nark that belongs to a neutralon A can interact with a nark that belongs to another neutralon B. They are there for instance in and states.

For simplicity, we represent bosons by straight red lines and fermions by black lines. Every vortex joins two black lines and one red line to insure spin conservation. Arrows will only be used for charged particles, but all transformations obey the conservation

law for u-quantum numbers. The nark of A leaves this neutralon as an antinark by creating a gluon. This gluon is transformed into two narks. This restores the initial color state and creates an N₂ boson. Its nark is captured by the nark of B to create a gluon. Indeed,. This gluon merges with the initially emitted antinark and changes its color: The color-neutrality is preserved for both neutralons and the apparently magical coordination of these processes results from the coexisting fields of all real and virtual particles. They influence one another.

We recall that nucleons are moving inside nuclei in the average field, created by its interactions with neighboring nucleons. This allows for shell-model structuring, excitations, fusion and fission processes. That has also to be expected for neutralons in compound DM particles. There will thus be “magic numbers” for more stable DM particles. However, the cold cosmic DM gas does usually not allow for sufficiently powerful collisions to excite DM particles. Elastic scattering will predominate, because of energy quantization. It requires only that DM particles come close enough to one another to be deviated by exchanging N₂ bosons. The cosmic DM gas is thus similar to usual gases. It has some pressure. Because of their mass, DM particles are also subjected to gravitational forces. This accounts for many astrophysical observations [13] .

The concept of self-interacting cold DM has independently been advanced for the same reason [14] . It has been confirmed by simulations [15] [16] , but the basic mechanism is that of Figure 8. A large cross-section for elastic scattering would imply a relatively low mass of N₂ bosons and a sufficient long lifetime. However, collisions between compound DM particles can also be hard enough to cause individual or collective excitations of neutralons. DM physics is similar to nuclear physics, but we have to stress the fact that the cosmic DM gas allows for fusion and fission processes, since they are very important for cosmology [7] .

5. Detection and Identification of DM Particles

5.1. Possible Signals of Cosmic DM Particles

Their detection requires special instruments, but they exist already and did even provide some enigmatic results. NASA’s Fermi Large Area Telescope (LAT) detected 130 GeV gamma-rays coming from galaxies. Their spatial distribution suggests that they are produced in galactic DM halos [17] [18] . According to STQ and the resulting concept of DM particles, this type of signals could be due to collisions between DM particles that confer enough energy to a particular nark to allow for the creation of a pair of gluons. Such a process is illustrated in Figure 9. The nark changes its color from to, by creating a gluon, but the nark does immediately recover its initial color by creating a gluon. For the represented sequence, this gluon is annihilated first, by creating an electron and an exited position: . This colored lepton and the gluon create together a normal positron:. The electron emits a photon, while the electron-positron pair is annihilated by creating another photon. This yields a pair and could occur quite frequently where the density of DM particles is high.

The Alpha Magnetic Spectrometer (AMS-02), attached to the International Space Station, revealed a surprising excess of positrons with respect to expectations for cosmic rays [19] . The fraction of the electron-positron flux increases from about 10 GeV up to 100 GeV and remains then nearly constant up to 350 GeV and even up to 500 GeV. It has been suggested that these positrons could result from dark matter decays. Pulsars can produce positrons of various energies, but the observed positron excess suggests a more general origin. The detection of an antiproton excess [20] would also be difficult to explain. To account for the threshold effect and the high energies of positrons in terms of DM particles, we can consider that collisions between two DM particles could lead to their fusion. This would liberate energy, since binding implies deeper negative energy states. This energy could be sufficient to fragment neutralons inside the resulting compound DM particle. When N₅ → N₃ + N₂ for instance, the N₂ boson could subsists for a short while by internal exchanges of gluons. Eventually, the nark and its antinark will annihilate one another.

They could then create a boson, when the excitation energy is superior to the required energy. This boson can decay into an pair (left part of Figure 10), but the metastable N₂ boson was excited inside the compound DM particle, while the electron and positron can leave the parent particle with a combined energy (right part of Figure 10). The threshold would then result from the minimal excitation energy. Since the boson can decay by creating hadrons [21] , this would also account for antiprotons. This scenario is hypothetical, but indicates that the conservation law for u-quantum numbers can be helpful to understand possible signals.

5.2. Direct Detection or Production

Since so-called “direct detection” of DM particles would be very important, several searches are presently undertaken by means of sophisticated equipment in underground facilities. This endeavor is partly inspired by experimental neutrino research and presumes that DM particles can interact with nucleons. The resulting nuclear recoil might then be detectable by some energy transfer, causing minute effects of various types. However, it is usually assumed that DM particles are WIMPS or some other hypothetical particles. Would the concept of DM particles resulting from STQ also allow

for interactions with nucleons? A single free nark can interact with a single free quark, by exchanging gluons, but this was only possible during the Big Bang. In the present universe, narks and quarks are separately bound together. They are constantly exchanging gluons, but inside different entitities.

Since compound particles have to remain color-neutral, a nark that belongs to a DM particle and a quark that belongs to a nucleon could exchange one color-neutral gluon, a pair of gluons, an N₂ or Z boson. These intereactions are not impossible, but will be softer and much less probable than strong interactions between quarks inside nucleons and narks inside neutralons. Astrophysical evidence indicates also that interactions between cosmic DM and baryonic matter are negligible and so far, even the most sensitive DM detector did not yield any evidence of interactions between DM particles and nucleons [22] . However, we will show that DM particles can interact with electrons [13] .

Could STQ justify the hope to discover physics beyond the SM by means of proton-proton collisions at the Large Hadron Collider of CERN? One possibility would be to detect pairs, produced by a process like that of Figure 9. It is sufficient to replace there the nark by a quark. It is electrically charged, but transformations like and would also create a pair of gluons. When sufficient energy is available, they could yield an electron-positron pair by means of an excited electron or positron. The resulting pair would then be detectable. This is possible as well for d-quark as for u-quarks, but resonances may occur at different energies.

Another process that could also produce pairs is represented in Figure 11. It includes the relevant u-quantum numbers for checking their conservation. We consider here a u-quark that creates a nark and its antinark. The resulting N₂ boson can produce an electron-positron pair that is annihilated. Such a resonance would be very remarkable, since it implies the creation of DM particles. Moreover, it would involve super symmetric partners of a quark and an excited lepton.

The discovery of a mysterious diphoton resonance at about 750 GeV was announced in 2015 and then reported to be only a statistical fluctuation. The actual data is more complex [23] [24] and will require further studies. If it were possible to detect a virtual N₂ boson, the resonance could determine its mass. Anyway, we are entering an era

where detection and identification of DM particles is becoming a realistic goal. The Chinese satellite DAMPE (Dark Matter Particle Explorer) was launched in December 2015 and is specifically equipped to yield complementary data [25] . The possibility of analyzing signals in terms of a conservation law, resulting from STQ may also be useful.

6. Conclusions and Applications

We started this investigation with a simple, but basic question: Are space and time continuous or not? We considered thus the value a of the smallest measurable length as being unknown and constructed a theory of Space-Time Quantization (STQ). It generalized Relativistic Quantum Mechanics to account for c, h and a. The highest possible energy of free particles in inertial frames is then. It is not infinite when. This allows for superluminal velocities at extremely high energies, but there are no logical inconsistencies. We could thus not exclude that space and time are quantized.

It appeared then that the existence of a finite limit for the smallest measurable length accounts also for elementary particle physics. Empirical data have been described and organized by means of the standard model. This required the introduction of phenomenologically defined concepts, but the resulting spectroscopy could not be explained. We ignored even why there are elementary particles and why they are characterized by quantized observables, obeying specific rules. This can be clarified when space and time are quantized. It is necessary, however, to realize that ideally precise measurements of spacetime coordinates do yield different lattices for possible results.

The “normal lattice” of lattice-constant a includes the origin of the reference frame, but there are also other lattices. They are displaced with respect to the normal lattice by along the chosen reference axes. The directions and orientations of these axes can be chosen in a completely arbitrary way, but space is three-dimensional. Quantum- mechanical functions have to be defined on all these lattices and can differ on the intercalated lattices with respect to the normal lattice. The essential point is that quantum-mechanical functions are epistemological tools, which allow us to store information by means of possible variations of for any given reference frame. The continuum assumption concealed some possibilities.

Large-scale variations define “states of motion” in terms of possible wavelengths and frequencies. By multiplexing, they are compatible with different types of variations at the smallest possible scale in space and time. They define “particle states” in terms of four quantum numbers, specifying relative phases for functions on intercalated lattices with respect to the normal lattice. It appears also that transformations of elementary particles into one another and resulting interaction are subjected to very strict conservation laws for these quantum numbers.

Although we are accustomed to consider that particles carry some energy, electric charge and other observable properties, they can also be viewed as being excitations of space and time. The four new quantum numbers are always and everywhere identical in the whole universe for a given type of particles. They are also independent of the chosen reference frame. These consequences of STQ agree with a great amount of already known empirical results in elementary particle physics. We understand for instance why the Standard Model of elementary particle physics required that quarks have 3 possible color states and that there are (at least) three generations of elementary particles. We can thus conclude from actual observations that STQ is real. It is not necessary to assume the existence of additional dimensions to account for elementary particle physics, since the usual 4-D space-time is sufficient when. It is not even necessary to know the actual value of the smallest measurable length.

STQ generalizes the Standard Model and accounts in particular for the nature and basic properties of DM particles. STQ could thus also be helpful for the detection and identification of DM particles. It opens a wide field of research in cosmology and astrophysics. We will provide some examples [7] [13] . Here, we have shown that it is possible to enlarge the foundations of physics by means of a natural extension of the theory of relativity and quantum mechanics.

Cite this paper

Meessen, A. (2017) From Space-Time Quantization to Dark Matter. Journal of Modern Physics, 8, 35- 56. http://dx.doi.org/10.4236/jmp.2017.81004

References