Received 25 July 2016; accepted 5 August 2016; published 8 August 2016

ABSTRACT

The work gives a natural explanation for the ordinary and dark energy density of the cosmos based on conventional quantum mechanical considerations which dates back as far as the early days of the quantum theory and specifically the work of Max Planck who seems to be the first to propose the possibility of a half quanta corresponding to the ground state, i.e. the energy zero point of the vacuum. Combining these old insights with the relatively new results of Hardy’s quantum entanglement and Witten’s topological quantum field theory as well as the fractal version of M-theory, we find a remarkably simple general theory for dark energy and the Casimir effect.

Keywords:

Half Quanta, Dark Energy, Hardy’s Entanglement, Casimir Energy, Topological Quantum Field, Witten’s Theory, Pointless Geometry, Non-Commutative Geometry, Fractal Spacetime, Dark Matter, tHooft Renormalization, E-Infinity Theory, Cantor Sets

1. Introduction

The true nature and origin of dividing energy into two main categories namely ordinary energy which we are able to measure and dark energy which should be there but could not be found or measured in any direct way is one, if not the most puzzling questions of modern science [1] - [6] . In a large number of papers, this question was answered and we think satisfactorily solved by the Author and his associates using mainly advanced mathematics and novel theories about spacetime [7] - [14] . However, and in all fairness to the readers as well as to ourselves, it seems that in the heat of the battle of resolving the mystery of dark energy which came upon all of us as a sudden shock, we seem to have overlooked more conventional elements which may have helped us and others in understanding the main problems within a more conventional framework.

The present work sprang out of such a realization and our final result and explanation of Casimir energy [15] - [17] , ordinary energy and dark energy [18] - [20] is basically a synthesis of an old well known proposal by Max Planck [21] [22] , conventional quantum mechanics [23] , Witten’s topological quantum field theory and M-theories [24] - [27] and last but not least, Hardy’s marvellous result of his gedanken experiment on quantum entanglement [28] [29] . How this is actually done will be shown in what follows. We should also add that we divided the references in the present paper into two parts where Refs. [1] - [76] are the main readings while Refs. [77] - [119] are additional readings which we think deepen and enhance understanding of the subject.

2. Max Planck Half Quanta

We know very well, at least since J. von Neumann’s pointless continuous geometry [30] [31] and A. Connes’ noncommutative geometry [32] [33] that the definition of a point in classical geometry is totally inadequate on both the philosophical and the pure mathematical level [34] [35] . Thus apart of the Heisenberg uncertainty principle, the statement that energy could be zero within a theory based entirely on probability like quantum mechanics cannot be right [23] . Luckily we all know the quantization recipe in quantum mechanics whether found algebraically or using any other method leads to the following famous energy levels equation [23]

(1)

where 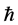is the Planck reduced constant and w is the frequency. In the above formula n can take only integer values, namely 1, 2, 3, ∙∙∙ because there can be no half 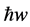in quantum mechanics since a photon is an elementary particle, in fact the most fundamental elementary messenger particle of them all and 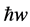has the same physical meaning as a photon [23] . The more surprizing it must be for the uninitiated to see that even when we have no photon at all, meaning when n = 0, then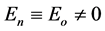, i.e. is not zero but a most recognized value given by [23]

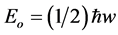(2)

The innocent conclusion of the above half quanta is that our postulate gained mainly from experiments that quanta are indivisible cannot be as straight forward as one could naively have thought and who knows, it may open the door to unsuspected connections related to fractional-Hall effects and similar things [119] . Historically speaking this (1/2) which ought to be quite famous because it gives a clear justification for the Casimir effect, goes back to the pioneering efforts of Max Planck to make sense out of his own discovery of the quantization of energy [21] - [23] . In the present work we hope that the reader will also see in the same way that this half is the first step on the road to understand ordinary energy and dark energy [15] - [20] .

3. Hardy’s Amazing Quantum Entanglement Result

As far as the present Author is concerned there are few modern results in quantum physics that can rival Hardy’s magnificent gedanken experiment regarding the maximal quantum entanglement probability for two quantum particles [28] [29] . The exact answer is found by Hardy using Dirac’s formalism to be [29] .

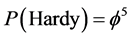(3)

where in full agreement with experiments [4] - [6] . The implications and ramifications of this exact result for physics and quantum cosmology are tremendous and are amply documented by the hundreds of papers published in the last ten years on this subject by many authors all over the world [2] - [6] . In the next section we will see how 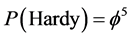could be interpreted as a dimensionless, topological Planck constant and how it relates to the zero point energy.

4. The Topological Quantum Field Theory and the Fractal Version of Witten’s M-Theory

Quantum field theory is primarily concerned with investigating the topological invariants of a theory and is the result of pioneering efforts of Schwartz, Attaya, Donaldson and Witten [24] - [26] [36] . It is not possible to overestimate the importance of the work done on this subject. It is equally impossible that the work of the present Author could have seen the light without the work of L. Hardy and Witten’s work, particularly his M-theory as well as his five D-branes in eleven dimensional spacetime model [37] . In fact looking at our own work in the last ten years it appears as if it was a realization of Koester’s sleep-waking hypothesis [38] where our mind was working almost subconsciously at night and consciously during the day on finding hidden connections and links between Witten’s theory, hardy’s result and our own efforts to formulate an exact non-classical spacetime theory guided by Ord-Nottale’s fractal spacetime theory [9] - [13] . At the end it becomes evident that 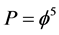may be seen as a topological Planck energy while the inverse 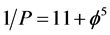is a topological cosmic distance also playing the role of the dimensionality of the fractal counterpart of Witten’s M-theory as developed by the present Author [27] . We discuss all of that in the next section.

5. The Unifying Power of a Bird’s Eye Topological View

We all have a pretty reasonable understanding and intuitive feel for what a topological dimension means. However what exactly is a Hausdorff dimension [39] ? In nonlinear dynamics the word fractal dimension is used to mean more or less the same as the Hausdorff dimension [39] . Consequently we may see the Hausdorff-fractal dimension not as a normal dimension but as a measure for the irregularity of a fractal shape, its ruggedness or smoothness. This understanding of the Hausdorff dimension brings into it the meaning of entropy which measures the degree of disorder in a system [5] [54] . Proceeding in the same direction it is reasonable to associate the Hausdorff dimension via entropy with energy which is not a stretch [40] . Remembering that our random triadic Cantor set used to model space and time had a Hausdorff dimension equal 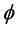as per a theorem due to American mathematicians Mauldin and Williams [7] [41] and remembering also that the result was found using this “Cantorian” theory, then due to what we said earlier on 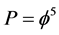could be seen not only as a probability but also as energy, albeit a “topological” energy [7] [14] [42] . Our reasoning is based on the following: First quantum entanglement may be loosely likened to a force acting instantly at a distance and second the probability of finding a point in a Cantor set was fixed not combinatorically because we have infinitely many points, nor geometrically because we have a zero measure [43] but topologically because the Hausdorff dimension is a finite positive value equal 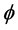so that we may write:

(4)

where the length of the unit interval within which the random Cantor set lives is unity. That way we see that may indeed be seen as a maximal topological energy unit similar to being our minimal Planck energy unit. By contrast smaller topological probabilities are possible so that for infinitely many entangled points we have [28]

(5)

which is what we find in our classical world where we are dealing with almost infinitely many particles and that is why in classical mechanics we do not have measurable entanglement of any kind. From the preceding discussion we see clearly that we could replace by and we assure the reader that this is a sound and bold move which will pay off dividend as we will see in the next section.

6. From Planck’s Half Quantum to Dark Energy via Ordinary and Casimir Energy

Let us now synthesize and fuse together the preceding result and discussion into a single coherent unity. We start with stating the final result. This is first that the vacuum zero point energy is found from replacing by and is consequently equal to the ordinary energy density of the cosmos [44] - [57]

(6)

Second this energy is clearly the cause behind the Casimir effect which is observed via a change of the boundary condition created by the two uncharged but conducting Casimir plates brought at nano distance of each other [15] - [17] [22] . Third, since the boundary condition is the crucial element in the Casimir effect experiment, it follows that at the hyperbolic horizon of our universe we have a one sided boundary condition akin to a one sided Möbius strip but in higher dimensions [65] converting the “local” Casimir effect “energy” into a global dark energy “effect” pushing the boundary of the holographic boundary of the universe and causing the observed accelerated expansion of the cosmos [58] - [62] . Seen that way we may rewrite in terms of Einstein’s maximal energy density but using instead of. Proceeding this way one finds [1] - [3] [66] .

(7)

This clearly means that E_o is in this case equivalent to the ordinary energy density of the cosmos E(O):

(8)

Consequently it follows that the dark energy density is simply [1] - [3] [66]

(9)

Comparing these results with the actual cosmic measurements of WMAP, Planck and type 1a supernova [50] - [57] we find that they are in excellent agreement as well as being identical to the result obtained previously using many different methods and models [1] - [6] .

7. Deriving Einstein’s E = mc² from Quantum Mechanics and Planck’s Half Quanta

The result that leads us to ponder if we could retrieve Einstein’s celebrated formula, namely E = mc², from it [1] - [6] . That could be seen as a brand new derivation of E = mc² using ironically quantum mechanics which Einstein was not able to bring himself to embrace without many reservations to say the least [67] . There are at least two ways to derive E = mc² from the above. First we have to admit that E = mc² is already included in. However E_o was not found by appealing to any spacetime. It is simply the vacuum energy density so that to find the entire energy density of our spacetime it should be multiplied with the topological “volume” of our spacetime [1] - [14] . We could argue now that a Hausdorff dimension is partially dimension and partially volume because it is based on a covering procedure. So we could multiple E_o with the Hausdorff dimension of our spacetime and expect to find a reasonable answer. However what is the Hausdorff dimension of our universe? One could be tempted to answer hastily that it is our Cantorian spacetime expectation value for the Hausdorff dimension of spacetime. However this is not correct. The correct answer is to use the topological rectangular “volume” resulting from multiplying the “Bosonic” dimension with the spin 1/2 fermionic dimension [7] [63] [64] and finding a practically super symmetric volume [52] - [62]

(10)

This is twice the dimension of the fractal version of Witten’s M-theory. Proceeding this way one finds [27]

(11)

The second possibility is far more straight forward and is nothing more than adding E_o = E(O) and E(D) together and finding that [27] [35] [39]

(12)

Either way we see that E = mc² consists of two quasi quantum components well hidden inside the deceptively simple Einstein’s beauty E = mc² [119] . We could touch upon trisecting E = mc² not only into two parts E(O) and E(D) but into three parts making a distinction between dark matter energy E(DM) and pure dark energy D(DE) where. The situation in this case is not straight forward because E(DM) and E(DE) are at least mathematically coupled. To show what we mean we recall our earlier published results that [68]

(13)

while

(14)

In the case of writing E in three parts, we cannot escape the coupling term which cancels out at the end in the following fashion [68]

(15)

where is ‘tHooft’s renormalon [118] and the coupling is given by

(16)

This coupling could be taken to be approximately. At the end cancels out and we find [68]

(17)

exactly as should be.

8. Conclusion

We gave a derivation for the ordinary energy density and the dark energy density of the universe starting from and based upon conventional and generally accepted quantum mechanical principles. In particular we relied upon a fact introduced probably for the first time by Max Planck, which shows that even in the absence of any real photon, completely empty spacetime has a non-zero energy. From there we went on to show that using this half quanta of Planck which is in the meantime part of most text books on quantum mechanics, we can explain not only the Casimir effect but could also explain the division of energy into ordinary measurable energy as well as dark energy which we cannot measure directly. Thus unlike our previous publications, we did not need to invoke new advanced mathematics nor really any new concepts beyond what one is taught in an advanced course or two in a good university undergraduate program in physics.

Cite this paper

Mohamed S. El Naschie, (2016) Max Planck Half Quanta as a Natural Explanation for Ordinary and Dark Energy of the Cosmos. Journal of Modern Physics,07,1420-1428. doi: 10.4236/jmp.2016.712129

References