Journal of Modern Physics
Vol.07 No.13(2016), Article ID:70555,7 pages
10.4236/jmp.2016.713149
Effects of Band Nonparabolicity and Band Offset on the Electron Gas Properties in InAs/AlSb Quantum Well
Gafur Gulyamov1, Bahrom Toshmirza O’g’li Abdulazizov2, Baymatov Paziljon Jamoldinovich2
1Namangan Engineering-Pedagogical Institute,
2Namangan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 13, 2016; Accepted: September 10, 2016; Published: September 13, 2016
ABSTRACT
One-band effective mass model is used to simulation of electron gas properties in quantum well. We calculate of dispersion curves for first three subbands. Calculation results of Fermi energy, effective mass at Fermi level as function of electron concentration are presented. The obtained results are good agreement with the experimental dates.
Keywords:
Quantum Well, In-Plane Dispersion, InAs, AlSb, Two Dimentional Electron Gas, Effective Mass, Cyclotron Mass

1. Introduction
In semiconductors, InAs and InSb of the conduction band are characterized by a strong nonparabolicity and recently intensively studied heterostructures based on them [1] - [3] . Nonparabolicity of the conduction band and the nature of the spin splitting of the electron in the quantum well (QW) are studied by the cyclotron resonance [4] - [7] .
In [8] has been investigated InAs/AlSb based QW with well width L = 15 nm, where two dimensional (2D) electron concentration ranges from 2.7 × 1011 to 8 × 1012 cm−2. In this work has been found increase of the effective mass of almost 2 times.
The purpose of this work―the calculation of: 1) subbands dispersion curves, 2) the density of states of 2D electron gas and 3) concentration dependence of effective mass in Fermi level for InAs/AlAs QW with width L = 15 nm.
It is shown that an abrupt change in the density of states leads to a peculiar change in the concentration dependence of effective mass.
2. The In-Plane Dispersion
Consider a single QW with width L (area A―InAs), concluded between barriers with height V (area B―AlAs). The energy is measured from the bottom of the band of the bulk InAs.
In the one band effective mass approximation, the solution of the three-dimensional Schrödinger equation can be represented as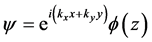 . Then for the area A and B, respectively, we can write the following one-dimensional equations
. Then for the area A and B, respectively, we can write the following one-dimensional equations
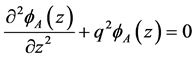 ,
,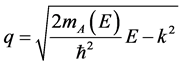 (1)
(1)
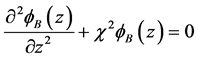 ,
,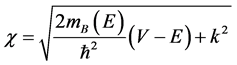 (2)
(2)
Here 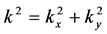 and
and 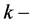 is in plane wave vector,
is in plane wave vector,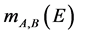 ―energy-dependent effective mass of the electrons in the material A or B. Solving Equations (1) and (2), using the boundary condition
―energy-dependent effective mass of the electrons in the material A or B. Solving Equations (1) and (2), using the boundary condition
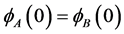 ,
,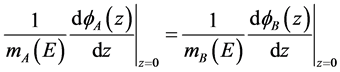 (3)
(3)
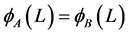 ,
,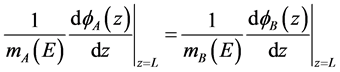 (4)
(4)
we find the dispersion equation
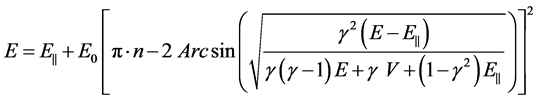 (5)
(5)
here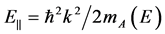 ,
, 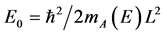 ,
,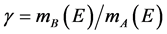 .
.
Nonparabolicity of conduction band well takes into account by formulas
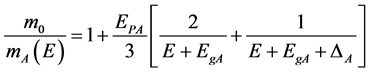 (6)
(6)
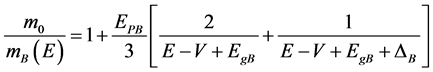 (7)
(7)
where,



To describe the statistics of electrons, Equation (5) is non convenient because it is not solvable with respect to E or k. Therefore, we replace Equation (5) is by simple approximation

Table 1. Band parameters of InAs and AlSb.
where, En―is bottom of n-th subbands. Now, approximation (8) is the best solution of (5). However, values of En in (8) now are obtained from Equation (5) at k = 0 by use numeric method.
For InAs/AlSb QW with L = 15 nm, we have: E1 = 0.0454 eV, E2 = 0.158 eV, E3 = 0.304 eV, and for case L = 6 nm we have: E1 = 0.163 eV, E2 = 0.509 eV, E3 = 0.903 eV.
Calculated dispersion curves from Equation (5) and approximation (8) are compared in Figure 1(a), Figure 1(b).
From Figure 1(a), Figure 1(b) follows that, the approximation (8) is sufficiently accurate and/or (8) is the best solution of (5) in a wide range of width QW. It is convenient when studying the statistics of electrons, kinetic, optical, or other characteristics of the 2D electron gas. Inconveniences approximation (8) is such that 

3. The Fermi Energy and Thermodynamic DOS
The total electron concentration is

where

According (8) we have


where
In Equation (10), the terms in the sum should be positive. The negative terms in 




From (10), we can estimate the critical concentrations of

Figure 1. The dispersion curves of the first three subbands (n = 1, 2, 3) in InAs/AlSb QW: the full (red) line―according to Equation (5), the dotted (blue) line―approximation (8); (a) L = 15 nm, (b) L = 6 nm.
with the well width L = 15 nm can be found

This estimation is close to experimental measured date 


The dependence 






These fractures occur at the critical concentrations of

The thermodynamically DOS of electron gas at Fermi level 
4. The Cyclotron Mass
According approximation (8), the electron effective mass at the Fermi level (cyclotron mass) 

The dependence 
This dependence can be obtained from Equations (10) and (12) by changing the Fermi energy in the range
This figure shows also the dependence of experimentally measured value of the effective masses (cyclotron mass) 






Figure 2. The dependence of the Fermi energy on the 2D concentration in InAs/AlSb QW with L = 15 nm, V = 1.35 eV. The critical points



Figure 3. The thermodynamically DOS of electron gas at Fermi level in InAs/AlSb QW, L = 15 nm, V = 1.35 eV.
Figure 4. The dependence of the effective mass on the total concentration for InAs/AlSb QW, L = 15 нм, V = 1.35 eV.
5. Conclusion
In this study are provided useful approximation (8) of subband dispersions and simplified Equation (10) to calculate the statistics of a degenerate electron gas in heterostructured InAs/AlSb QW, which satisfactorily describes the experimental results [8] . They are also useful to study of calculation of the transport, optical and magnetic properties of electron gas in a Kane type 2D system. The above description of the algorithms can be applied to other QW heterostructures based on semiconductor group
Acknowledgements
This work was supported by the Scientific and Technical program Republic of of Uzbekistan (Grant F2-OT-O-15494).
Cite this paper
Gulyamov, G., Abdulazizov, B.T. and Jamoldinovich, B.P. (2016) Effects of Band Nonparabolicity and Band Offset on the Electron Gas Properties in InAs/ AlSb Quantum Well. Journal of Modern Physics, 7, 1644-1650. http://dx.doi.org/10.4236/jmp.2016.713149
References
- 1. Vasilyev, Yu.B., Gouider, F., Nachtwei, G. and Buckle, P.D. (2010) Semiconductors, 44, 1511-1514.
http://dx.doi.org/10.1134/S1063782610110266 - 2. Spirin, K.E., Kalinin, K.P., Krishtopenko, S.S., Maremyanin, K.V., Gavrilenko, V.I. and Sadofyev, Yu.G. (2012) Semiconductors, 46, 1396-1401.
http://dx.doi.org/10.1134/S1063782612110206 - 3. Barate, D., Teissier, R., Wang, Y. and Baranov, A.N. (2005) Applied Physics Letters, 87, 051103.
http://dx.doi.org/10.1063/1.2007854 - 4. Yang, M.J., Lin-Chung, P.J., Wagner, R.J., Waterman, J.R., Moore, W.J. and Shanabrook, B.V. (1993) Semiconductor Science and Technology, 8, S129.
http://dx.doi.org/10.1088/0268-1242/8/1S/029 - 5. Yang, M.J., Lin-Chung, P.J., Shanabrook, B.V., Waterman, J.R., Wagner, R.J. and Moore, W.J. (1993) Physical Review B, 47, 1691.
http://dx.doi.org/10.1103/PhysRevB.47.1691 - 6. Gauer, C., Scriba, J., Wixforth, A., Kotthaus, J.P., Bolognesi, C.R., Nguyen, C., Brar, B. and Kroemer, H. (1994) Semiconductor Science and Technology, 9, 1580.
http://dx.doi.org/10.1088/0268-1242/9/9/002 - 7. Warburton, R.J., Gauer, C., Wixforth, A., Kotthaus, J.P., Brar, B. and Kroemer, H. (1996) Physical Review B, 53, 7903.
http://dx.doi.org/10.1103/PhysRevB.53.7903 - 8. Aleshkin, V.Ya., Gavrilenko, V.I., Ikonnikov, A.V., Sadofyev, Yu.G., Bird, J.P., Jonhson, S.R. and Zhang, Y.-H. (2005) Semiconductors, 39, 62-66.
http://dx.doi.org/10.1134/1.1852647







