Journal of Modern Physics
Vol.07 No.11(2016), Article ID:68366,4 pages
10.4236/jmp.2016.711117
Revised Quantum Electrodynamics in a Condensed Form
Bo Lehnert
Alfvén Laboratory, Royal Institute of Technology, Stockholm, Sweden

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 June 2016; accepted 11 July 2016; published 14 July 2016
ABSTRACT
This theory aims beyond the possibilities being available from the Standard Model. Examples are given by the directly obtained rest masses of the elementary particles, the deduced values of the elementary charge and of the mass of the boson detected by CERN which are close to their experimental data, and by an incorporated spin of the photon.
Keywords:
Quantum Electrodynamics, Zero Point Energy, Standard Model and beyond

1. Introduction
The main features and applications of the Revised Quantum Electrodynamic theory (RQED) by the author are presented in this condensed review, without detailed deductions which have been reported elsewhere [1] - [7] . The review starts from a specification of the domain of application in Section 2, and with identifications of the fundamental concepts which form the basis of the field equations of RQED in Section 3. This is followed by the applications to elementary particles with rest mass and spin, with net electric charge, and with intrinsic electric charges in Section 4. Some associated applications to cosmology are finally given in Section 5.
2. Domain of Application
The theory of Revised Quantum Electrodynamics includes fundamental physics, with microscopic applications to elementary particles as well as to macroscopic ones on cosmological scale. It leads to new results not being available from the Standard Model and conventional approaches, and it differs essentially from the theory by Higgs. The latter is due to multistage processes by which a heavy particle is created through nonlinear broken symmetry effects, and is then in its turn decaying into all less heavy particles.
This theory thus makes an attempt in the first place to give a picture of the fundamental properties of the less complicated elementary particles, such as leptons and the photon. Further investigations are needed on the bound quarks and on more complex and compound particles. In addition, the theory does not deal with the classical field equations which, in their turn, apply to the formation of macroscopic charge and mass densities due to already existing particles.
3. Basis of Present Theory
The RQED theory is based on a number of fundamental concepts:
・ From quantum theoretical analysis of the harmonic oscillator Planck has proved the existence of a lowest nonzero energy state, the Zero Point Energy (ZPE).
・ This state generally includes photon-like electromagnetic oscillations, with and without associated electric charges.
・ The ZPE fluctuations manifest themselves in the Casimir force which arises in vacuo between two metal plates separated by a small spacing. This is shown by experiments to result in a real macroscopic pressure. Consequently, the vacuum is not merely a state of empty space.
・ The ZPE and the Casimir force thus indicate that there are sources in the vacuum state which have to be included into the electromagnetic field equations. This leads to an incorporated four-current, associated with a nonzero electric field divergence, . The result of this is a broken symmetry of the electric and magnetic field strengths,
. The result of this is a broken symmetry of the electric and magnetic field strengths, 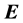 and
and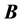 . The nonzero
. The nonzero  thereby increases the degrees of freedom of the system, acting somewhat like a hidden variable.
thereby increases the degrees of freedom of the system, acting somewhat like a hidden variable.
・ Spatial integration of  over the volumes of corresponding particle models leads both to nonzero and zero net electric charges, as well as to intrinsic charges of both polarities.
over the volumes of corresponding particle models leads both to nonzero and zero net electric charges, as well as to intrinsic charges of both polarities.
・ The extended electromagnetic field equations of RQED still become both Lorentz and gauge invariant. Relativity in the form of Lorentz invariance does not only apply to plane electromagnetic waves, but also to other geometries such as to cylindrical waves.
・ The quantized electrodynamic field equations become identical with the original equations in which the potentials and current densities are replaced by their expectation values.
・ The conventional theory on the ZPE frequency spectrum is unacceptable, because it is underdetermined, treats all states with the same statistical probability of unity, and leads to an infinite total energy density. This problem is eliminated by the inclusion of a Boltzmann factor in a revised form of the spectrum deduced from conventional statistical theory.
The revised four-dimensional field equations of the vacuum state thus have the form [1]
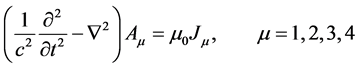 (1)
(1)
with
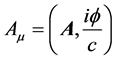 (2)
(2)
standing for the four-potential and
 (3)
(3)
for the four-current density representing a source due to the electric charge density
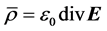 (4)
(4)
Here 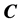 is a velocity vector defined by
is a velocity vector defined by
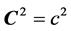 (5)
(5)
to make its modulus equal to the scalar velocity constant c of light. Thus 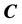 is a vector with up to 3 com- ponents. An example is given by screw-shaped cylindrical electromagnetic waves forming a photon, where
is a vector with up to 3 com- ponents. An example is given by screw-shaped cylindrical electromagnetic waves forming a photon, where  has two components, one related to the direction of propagation and one being associated with nonzero spin.
has two components, one related to the direction of propagation and one being associated with nonzero spin.
The original form of the field equations in an empty vacuum state are on the other hand given by 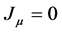 in Equations (1) and (3), by
in Equations (1) and (3), by  in Equation (4), and by
in Equation (4), and by 
4. Applications to Elementary Particles
The applications of RQED to elementary particles are based on field equations in vacuo with broken symmetry due to a nonzero
4.1. Particles with Rest Mass and Spin
In all particle models of RQED the source terms due to broken symmetry give rise to steady states having a nonzero rest mass and an associated nonzero spin:
・ This applies to particles with net charge such as the electron, muon, and tauon where the product

quantity. Such particles are prevented by the included magnetic field from “exploding” under the action of their electrostatic eigenforce.
・ An example of particles with vanishing net charge is the Z boson for which a mass of 91 GeV becomes connected with a characteristic radius of about 10−18 m. A superposition of two such particles with opposite and cancelling magnetostatic potentials leads to a composite purely electrostatic and unstable boson, having no net charge, no magnetic field, no spin, and a minimum mass of 125 GeV within a limit of error of only a few percent [4] . This deduced particle state agrees with all the basic properties of the particle recently detected by CERN, but it has no relation to the theory by Higgs with its associated multistage processes of decaying particles. In addition, the latter theory does not predict the exact value of the resulting boson mass.
・ A screw-shaped model for the individual photon results from RQED theory. It includes a spin at the expense of a very small reduction of its phase and group velocities from the velocity constant c, i.e. only in the ninth decimal of c. The spin is then associated with a very small but nonzero photon rest mass. Without broken symmetry and with a vanishing
・ The present photon model contributes to the understanding of the wave-particle dualism, the observed needle radiation, the photoelectric effect, and of two-slit experiments.
4.2. Particles with Net Electric Charge
Particles with net integrated electric charge, such as the electron, muon, and tauon, are given by divergent corresponding generating functions and point-charge-like geometries:
・ Convergent integrated final results are still obtained, in terms of a revised renormalization procedure.
・ The theory results in a deduced fundamental charge constant



4.3. Intrinsic Electric Charges
The broken symmetry also results in substantial intrinsic charges of both polarities within the volume of a particle, in the cases with as well as without net integrated charges:
・ Examples are given in which these intrinsic charges become an order of magnitude larger than the net inte- grated charge [5] .
・ The corresponding short-range Coulomb interaction between two such particles is then expected to become two orders of magnitude larger than the interaction due to the net charges, i.e. of the same magnitude as the strong force.
・ This raises the question whether the interaction due to the intrinsic forces will interfere with the strong force, or become an explanation of the latter. This requires further investigations.
5. Applications to Cosmology
As based on the revised form of the ZPE frequency spectrum, the following results are obtained on cosmological scale where gravity becomes important:
・ A new interpretation of dark matter and dark energy has been proposed. Dark matter is considered to ori- ginate from the ZPE density which leads to a contracting gravitational force, whereas dark energy originates from the ZPE density gradient leading to an expansive force [6] [7] .
・ In this way dark matter and dark energy are due to the same common ZPE spectrum, and this resolves the difficulty with the cosmological constant. It also resolves the related coincidence problem of equal magni- tudes of dark matter and dark energy, i.e. near an equilibrium of the corresponding forces.
・ In an application to the observable universe having a radius of about 1026 m, and with the present estimated proportions of dark matter, dark energy, and normal matter given by the astronomers, the present theory would result in in a deduced ZPE density of about
・ An experimental method in determining the ZPE density at the Earth's orbit has been proposed. It is based on measurements on the maximum Casimir force between two plates of different metals and at a vanishing air gap.
6. Summary
Conventional theory and the Standard Model including the approach by Higgs are based on a vacuum state of empty space. This leads to severely restricted forms of the corresponding solutions. These limitations can be removed by the present theory which opens a number of new possibilities beyond those so far being available. Examples are given by directly obtained rest masses of the elementary particle models, the deduced values of the elementary charge and of the mass of the boson detected by CERN being close to their experimental data, the incorporated spin of the individual photon, the large intrinsic charges of particle models and their possible relation to the strong force, and the revised ZPE frequency spectrum with its proposed relation to dark matter and dark energy. All results described in Sections 4 and 5 are thus based in the common concept of a Zero Point Energy.
Cite this paper
Bo Lehnert, (2016) Revised Quantum Electrodynamics in a Condensed Form. Journal of Modern Physics,07,1316-1319. doi: 10.4236/jmp.2016.711117
References
- 1. Lehnert, B. (2013) Revised Quantum Electrodynamics. In: Dvoeglazov, V.V., Ed., Contemporary Fundamental Physics, Nova Science Publishers, Inc., New York.
- 2. Lehnert, B. (2015) Journal of Modern Physics, 6, 448-452.
http://dx.doi.org/10.4236/jmp.2015.64048 - 3. Lehnert, B. (2015) Journal of Modern Physics, 6, 1695-1700.
http://dx.doi.org/10.4236/jmp.2015.611171 - 4. Lehnert, B. (2015) Journal of Modern Physics, 6, 2974-2079.
- 5. Lehnert, B. (2013) Progress in Physics, 3, 17-20.
- 6. Lehnert, B. (2013) Journal of Plasma Physics, 79, 327-334.
http://dx.doi.org/10.1017/S0022377812001055 - 7. Lehnert, B. (2016) Journal of Modern Physics, 7, 1112-1119.
http://dx.doi.org/10.4236/jmp.2016.710100


