Received 13 April 2016; accepted 20 May 2016; published 23 May 2016

ABSTRACT

A comparative analysis of a model of complex scalar field f and real scalar field c with interaction 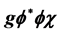for the real and purely imaginary values of coupling g in perturbative and non-perturbative regions is provided. In contrast to the usual Hermitian version (real g), which is asymptotically free and energetically unstable, the non-Hermitian PT-symmetric theory (imaginary g) is energetically stable and not asymptotically free. The non-perturbative approach based on Schwinger- Dyson equations reveals new interesting feature of the non-Hermitian model. While in the Hermitian version of theory the phion propagator has the non-physical non-isolated singularity in the Euclidean region of momenta, the non-Hermitian theory substantially free of this drawback, as the singularity moves in the pseudo-Euclidean region.

Keywords:

Scalar Field Theory, Non-Hermitian Lagrangians, Schwinger-Dyson Equations, Asymptotic Behavior

1. Introduction

Non-Hermitian PT-symmetric quantum models, open at the end of the last century [1] , currently have a wide use in various fields of physics (see review [2] and references therein). For a quantum field theory the introduction into circulation the non-Hermitian PT-symmetric models is interesting as an extension of a narrow class of Hermitian models with acceptable physical and mathematical properties (such as stability, unitary, and renormalisability) and opens new possibilities for describing the properties of high-energy particles.

In works of Bender et al. [3] [4] the PT-symmetric model of a scalar field with the interaction 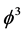has been investigated. As has long been known (see [5] ), the Hermitian version of this model is asymptotically free, but the unstability of the cubic interaction leads to the fact that models of this type previously considered exclusively as a methodical examples (see, for example [6] ). For the non-Hermitian version of this model with imaginary coupling, however, the main argument of the unstability―the cubic potential is unbounded below―becomes invalid since the set of complex numbers is not an ordered set. Moreover, in work [3] , the arguments are given in favor of energy stability of the non-Hermitian model with cubic interaction. The analysis of Bender et al. (see [3] [4] ) indicates that the 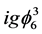theory is like a 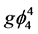theory: it is energetically stable, renormalized and has the trivial-type ultraviolet behavior, i.e., compared with the conventional model, the PT-symmetric 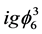theory exhibits new interesting properties.

In this paper we study the scalar Yukawa model, i.e., a model of a complex scalar field (phion) and a real field 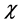(chion) with the interaction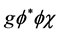. This model is used in nuclear physics as a simplified version of the Yukawa model without spin degrees of freedom, as well as an effective model of the interaction of scalar quarks [7] [8] . If the coupling constant g takes purely imaginary values and the field 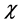is a pseudoscalar, such a model is PT-symmetric. As expected, this model is a very similar to the 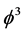theory. All arguments of Bender et al. (see [3] ) concerning the unstability of the Hermitian theory and stability of non-Hermitian PT-symmetric theory fully extended to the scalar Yukawa model. An additional argument is the consideration (in the spirit of [9] ) a zero-dimensional version of the theory. The partition function

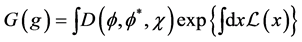
in a zero-dimensional space becomes the usual improper integral

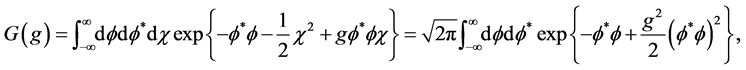
which converges for (non-Hermitian case) and diverges for 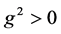(Hermitian case).

In the coupling-constant perturbation theory, this model also has a very similar to the theory. Section 2 briefly presents the results of the coupling-constant perturbation theory and based on the perturbation theory renormalization-group analysis for this model. As well as the theory the Hermitian scalar Yukawa model in a six-dimensional space is asymptotically free. The non-Hermitian scalar Yukawa model in the has, besides the Gaussian fixed point, also the non-Gaussian fixed point of Wilson-Fisher type. At the non-Hermitian scalar Yukawa model, as well as theory is ultraviolet unstable, and to describe the ultraviolet region we need to go beyond the perturbation theory.

Section 3 presents an attempt to go beyond the coupling-constant perturbation theory. The formalism of bilocal source is used to build a non-perturbative expansion of the system of the Schwinger-Dyson equations, and equation for the phion propagator in the leading approximation of this expansion is investigated. A remarkable property is established: for the Hermitian theory the phion propagator has a non-isolated singularity in the Euclidean region of momenta while for the Hermitian theory this singularity (an origin of a cut) moves in a pseudo- Euclidean region, i.e., from the point of view of the analytic properties the non-Hermitian theory is preferable.

2. Perturbation Theory and Renormalization Group

2.1. Perturbation Theory

We consider the model of interaction of a complex scalar field (phion) and a real scalar field (chion) with the Lagrangian

(1)

in a d-dimensional Euclidean space near. At the coupling g is dimensionless, and the theory contains ultraviolet divergences which can be eliminated with a standard recipe by the renormalization of fields and vacuum expectations (Green functions).

The perturbation theory on the renormalized coupling constant g gives us the following expressions for the renormalized 1PI functions:

Propagators of the phion

(2)

and of the chion

(3)

A vertex:

(4)

Here are the renormalized masses of the phion and the chion. are counter-terms of the renormalization of the masses and fields of the phion and the chion correspondingly, is a counter-term of the renormalizarion of coupling, and

In the dimensional regularization ():

Here is a ’t Hooft scale. We define the dimensionless coupling as

and by adopting the MS scheme [6] , we get the counter-terms:

(5)

2.2. Renormalization Group. Hermitian Theory

The independence of initial (bare) quantities and unrenormalized Green functions from the ’t Hooft scale leads to the renormalization group equation:

(6)

Here is the one-particle-irreducible function with n phion and l chion tails.

Counter-terms (5) allow us to calculate renormalization-group coefficients¹

(7)

(8)

(9)

(10)

These renormalization-group coefficients quite similar to corresponding coefficients of -theory (see [3] [6] ). As for -theory the scalar Yukawa model near possesses only a Gaussian fixed point, and near this point the couplings scale according their scaling dimension.

At the scalar Yukawa model is asymptotically free as the -theory. The running coupling (invariant charge) is a solution of equation

(11)

with the boundary condition Here.

For -function (7) the solution of this equation at is

(12)

i.e. the model possesses the typical asymptotically-free behavior at high momenta with all consequences.

2.3. Renormalization Group. Non-Hermitian Theory

For the non-hermirian PT-symmetric theory one should make the substitution

in formulae of above Subsections. Thus, the expression for -function takes the form

(13)

etc.

The situation in this case is also similar to -theory (see [3] ). -function vanishes, except of the Gaussian point, at the fixed point of Wilson-Fisher type:

(14)

Near the Gaussian point couplings are still defined by their canonical dimensions. Near the non-Gaussian fixed point (14) the scale behavior is modified in accordance with the linearized renormalization group equations. At fixed points merge into one Gauss point.

The running coupling in this case is

(15)

i.e., the theory at large momenta has the trivial-type behavior, and the perturbation theory in this asymptotic region cannot be applicable.

3. Beyond the Perturbation Theory

3.1. Shcwinger-Dyson Equations

To construct the non-perturbative approximation we will use the formalism of Schwinger-Dyson equations (SDE).

The generating functional of Green functions (vacuum averages) of the model with Lagrangian (1) is the functional integral

(16)

Here is the bilocal source of phions², j is the single source of chions.

The translational invariance of the functional integration measure leads to relations

and

which can be rewritten as the functional-differential SDE for generating functional G:

(17)

and

(18)

Here and are bare phion and chion masses. Equation (18) allows us to express all Green functions with chion legs in terms of functions that contain phions only. For logarithm this equation has the form

(19)

(Here)

The differentiation of (19) over gives us the three-point chion-phion function

(20)

where

(21)

is the two-particle phion function. The differentiation of (19) over j with taking into account Equation (20) gives us the chion propagator:

(22)

etc. Thus, for a complete description of the model we need to know phion Green function only.

Excluding with the help of the SDE (18) a differentiation over j in SDE (17), we obtain at the equation

(23)

which only contains the derivatives over the bilocal source.

Since, then Bose-symmetry entails the relation

reflecting crossing symmetry of the two-particle function, and, accordingly, the Equation (23) can be written as

(24)

Both equations give the same coupling-constant perturbation series, and are completely equivalent from the point of view of some visionary exact solutions of Schwinger-Dyson equations. However, these equations give different non-perturbative expansion. This is due to the incomplete structure of the leading-order multi-particle functions of such expansions in terms of crossing symmetry. It is a peculiar feature of some non-perturbative approximations. In order to restore crossing symmetry lost in the leading-order approximation, it is necessary to consider the next-to-leading-order approximation. (A more detailed discussion of this issue see in the papers [11] [12] and references therein).

Equation (23) can be used for the construction of the mean-field expansion (see [11] ). In the language of Feynman diagrams the leading order of this expansion corresponds to the summation of the chains and its structure actually reproduce the renormalization-group summation of the previous section.

In this paper we consider the expansion, based on the Equation (24) (see also [12] ). In the language of Feynman diagrams the leading order of this expansion corresponds to the summation of ladder graphs, so we'll call it the ladder expansion.

For logarithm this equation has the form

(25)

3.2. Legendre Transform

Equation

(26)

which determines the phion propagator can be regarded as an equation that determines implicitly as a functional of:

Assuming the unique solvability of the Equation (26), we can move to a new function variable and define the generating functional of Legendre transform

(27)

From definitions (26) and (27) it follows that

(28)

and SDE (25) takes the form

(29)

In this equation, it is assumed that is a functional of new functional variable, what can be done, using the condition of connection

(30)

which follows from the relation

3.3. Ladder Expansion

SDE (29) tells us a non-perturbative expansion of the generating functional, which based on the following leading approximation

(31)

Next-to-the-leading-order equation is

(32)

where is a functional of, defined by condition of connection (30).

At the source being switched off, Equation (31) is the equation for the leading-order phion propagator:

(33)

A differentiation of equation (31) on and taking into account connection condition (30) together with equation (20) gives us the equation for the three-point function:

(34)

3.4. Phion Propagator

Lets go to the Equation (33) for the phion propagator. To eliminate ultraviolet divergences in Equation (33) is sufficient to introduce counter-terms of phion-field renormalization and mass. The normalization of the renormalized propagator at zero momentum

leads to the renormalized equation in momentum space

(35)

where is the renormalized mass operator, and

Below we consider the case of massless chion:. In this case nonlinear integral Equation (35) can be reduced to an integral Volterra-type equation, which, in turn, is reduced to a differential equation. Using the formula of massless integration in six-dimensional space

(36)

we obtain

(37)

Introducing dimension-less function

where we obtain the integral equation

(38)

which is reduced to the non-linear fourth-order differential equation

(39)

This differential equation enables us to calculate the asymptotics of for large t:

(40)

where

i.e., for Hermitian theory with the asymptotic behavior becomes purely imaginary. In order to understand what is happening with the propagator in Euclidean region, consider a simplified model with the same UV behavior. This model is based on the following approximation of mass operator (37) in a high-momentum region:

(41)

The equation for the inverse propagator u takes the form:

(42)

The cutoff at the lower limit of integration is introduced in order to avoid mass singularities (in the case insignificant).

The exact solution of Equation (42) is

(43)

i.e., an asymptotic behavior at large momentum given by the same formula (40).

Thus, we can conclude that for the usual Hermitian theory with the propagator in the ladder approximation has the non-physical non-isolated singularity in the Euclidean region, while for the non-Hermitian theory with, this singularity moves in a pseudo-Euclidean region, i.e., the non-Hermitian theory is more preferable from the standpoint of the analytical properties of the propagator.

4. Conclusions

Our results demonstrate that the non-Hermitian PT-symmetric scalar Yukawa model has interesting properties

both perturbative and non-perturbative. In the perturbation region of small momenta, theory similar in their properties to Hermitian theory, i.e., energetically stable, has, in addition to the Gaussian

fixed point, a non-trivial fixed point of Wilson-Fisher type. As expected, the properties of the scalar Yukawa model in the perturbative region completely analogous to the corresponding properties of theory (see [3] ). The non-perturbative ladder expansion of Section 3 reveals new interesting feature of the non-Hermitian model. While in the Hermitian version of theory the phion propagator has the non-physical non-isolated singularity in the Euclidean region of momenta, the non-Hermitian theory substantially free of this drawback, as the singulatity moves to the pseudo-Euclidean region.

For a complete description of the leading-order ladder expansion, including its renormalization group analysis, it is necessary to solve Equation (34) for the three-point function. This is a very difficult task, since this equation contains a nontrivial phion propagator, described by Equation (33). Perhaps for the renormalization-group analysis, clarifying the nature of the behavior of couplings in the asymptotic region is sufficient to solve a more limited problem, namely the calculation of the vertex function at zero momentum (which is, however, also very difficult). We can assume that in the Hermitian case the theory retains the property of asymptotic freedom, and everything will return to own. For the non-Hermitian PT-symmetric theory a prediction of the answer is harder. In any case, the results indicate that the non-Hermitian scalar Yukawa model has, compared with the Hermitian version, a number of attractive features, which make it a very interesting object of study.

Acknowledgements

Author is grateful to the participants of IHEP Theory Division Seminar for useful discussion.

Cite this paper

Vladimir E. Rochev, (2016) Hermitian vs PT-Symmetric Scalar Yukawa Model. Journal of Modern Physics,07,899-907. doi: 10.4236/jmp.2016.79081

References

NOTES

¹We use the notations of Collins [6] . Note, that the complete renormalization-group analysis assumes also an addition the linear term in Lagrangian (1) and the corresponding counter-term. We omit this simple generalization of calculations as non-essential for our consideration.

²A formalism of the bilocal source was first elaborated in the quantum field theory by Dahmen and Jona-Lasinio [10] . We consider this using presumably as a convenient choice of the functional variable.