Journal of Modern Physics
Vol.06 No.15(2015), Article ID:61797,7 pages
10.4236/jmp.2015.615222
Probability and Curvature in Physics
Xinzhong Wu
School of History and Culture of Science, Shanghai Jiaotong University, Shanghai, China

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 24 July 2015; accepted 6 December 2015; published 9 December 2015

ABSTRACT
Probability concept in physics entered into statistical physics and quantum physics by molecules kinematics; and curvature concept in physics as applying differential geometry to physics, entered into analytical mechanics long ago. Along with introducing space-time curvature concept into general relativity, curvature concept became more important; gauge field theory regards field intensity as curvature of fibre bundles. Curvature concept in quantum mechanics germinated from original derivation of Schrodinger equation; catastrophe scientist Rene Thom advanced curvature interpretations of ψ function and entropy according to differential geometry. Guoqiu Zhao advanced curvature interpretation of quantum mechanics; this new interpretation made relativity theory and quantum mechanics more harmonious, and regarded ψ function as a curvature function. So far Zhao’s quantum curvature interpretation is nearest to Schrodinger’s scientific thought and Einstein’s physics ideal.
Keywords:
Probability, Curvature, Quantum Curvature

1. Probability Concept in Physics
Probability theory has a long history since Aristotle published his genetics work; many mathematicians and logicians developed probability theory since the 17th century. There are two types of probability interpretations: 1) probability is a confirmation measure of evidences; 2) probability is a relative frequency measure of a certain property emergence in a type of special elements ([1] , pp. 34-36).
Probability as a physical concept germinated from Aristotle’s potential concept. Newton mechanics developed into Laplace determinism by Spinoza’s rationalism. Classical rationalism considers that knowledge or science should be built on the base of a certain precise propositions or laws, but not on the base of experience by observations and experiments. These precise laws are inevitable and self-evident truths, and attainable directly by reason. Einstein followed Spinoza’s rationalism in his old age. When we lack knowledge about great natural laws, we introduce a priori probability concept as a measure of reasonable belief that is built on the base of “no difference principle”, but not on the base of experience discoveries ([1] , p. 35).
Probability concept in physics entered into thermodynamics and statistical physics by molecules kinematics. Maxwell introduced a statistical mean concept of molecules motion speeds in 1859. Boltzmann assumed the law of the equipartition of energy in 1871; the energy of molecules motions is well-distributed in the energy super surface of molecules momentum space. When we divide energy into infinite infinitesimal portions, we can obtain Maxwell distribution.
We express Newton mechanics in analytical mechanics by the phase space concept. A point in 6N dimensions phase space stands for the positions and motion speeds of N particles in 3-dimensional space. Previously Boltzmann defined the limit of τi/τ (when τ → ∞) as the probability of a thermodynamics system in Si state; τi is the interval of the system in Si state when we observe the system in τ period. Einstein preferred this thermodynamics probability definition to the later statistical weight definition of Boltzmann ([2] , p. 74).
A basic assumption in statistical mechanics is the principle of equal probability. The number of microscopic states Wx accessible to a macroscopic system (Ω kinds of microscopic states) is called the statistical weigh (thermodynamic weigh): Px = Wx/Ω. If we define entropy S by S = klnW, this is very convenient for deriving the thermodynamic relations from the statistical mechanical point of view; k is called Boltzmann constant. Macroscopic entropy is a measure of phase space volume of microscopic states. This means that entropy connects with information. The more entropy of a macroscopic state, the more its phase space volume, the more frequent its appearances, but the less its information, the more its molecule motions chaos.
Max Planck derived the black-body radiation law from experiments on October 19 in 1900; he introduced two hypothesis: 1) quantum hypothesis: the energy of an oscillator of frequency ν is quantized; only multiples of Planck’s quantum of energy E = hν are possible. 2) Statistical hypothesis: when we count entropy of oscillators, we regard oscillators as identical particles. So when P portions of quantum of energy are distributed among N oscillators, its statistical distribution is different from Boltzmann distribution.
Laplace’s demon who can calculate the whole universe states of past, now and future according to the knowledge about positions and speeds of the given particles, come to a deadlock in pace with the birth of quantum theory and the development of atom physics. Rutherford’s and Soddy’s radioactivity decay law −dn/dt = n/τ hints firstly that probability concept plays more basic roles in quantum theory than that in Laplace’s analysis mechanics and Boltzmann’s statistical mechanics. Einstein introduced statistical concept into his light quanta theory in 1905, and introduced transition probability concept in derivation of Planck radiation formula in 1917. Transition probability is similar to radioactivity decay probability 1/τ, these means that emission and absorption of radiation in matter obey probability law like radioactivity decay law, in contrary to classical determinism law ([1] , p. 52).
The popular formal system of quantum mechanics and its Copenhagen interpretation appeared in 1925-1926. Niels Bohr, W. Heisenberg and Max Born formed Copenhagen School. Copenhagen interpretation included two principles: 1) Complementarity principle; 2) Probability postulate. Max Born advanced probability interpretation in “Zur Quantenmechanik der Stossvorgange” in 1926, he regarded |y|2 as probability of a particle appearance. When quantum information transforms into classical information, Born’s quantum probability interpretation destroys a holomorphic conversion of ψ complex-variable function. Max Born wrote a letter to Einstein in 1926: “I regard Schrodinger wave field as ‘ghost field’ in your terms, this is useful then…, Of course, probability field doesn’t propagate in common space but in phase space (configuration space).” ([2] , p. 544).
Quantum mechanics probability interpretation germinated from Schrodinger’s paper “Quantisierung als Eigen went problem” (Ann.phys.81), at first he gave an electron density interpretation of wave function: “We choose a particle whose position be described by three coordinates in common mechanics, and let ψψ* integral along all surplus coordinates of a system, and then the integral result multiplies a constant what represents electric particle charge. We do identical operations on each particle (three coordinates sets), and give a same position to chosen particles in each situation, namely we want to know the position of electron density space, this electron density is equal to the sum of part results.” And then, Schrodinger points out: “ψψ* is a weigh function of configuration space of a system. Wave mechanics configuration of a system is the superposition of many configurations (strictly the superposition of mechanics configurations of all possible particles in kinematics). Like this, each particle’s mechanics configuration contributes to real wave mechanics configurations in a weigh given by ψψ*.” Schrodinger regarded ψ as extremely real fluctuations of effective charges space density in electrodynamics, and pointed out: “It is ψ function to allow these total fluctuations grasped by a single partial differential equation in mathematics. We have underlined this fact repeatedly: it is impossible to interpret ψ function itself in 3-dimen- sional space language, regardless of a single electron problem misleading us to this tendency, because ψ function is a function in a configuration space but not in a real physical space in general.” Also Schrodinger proved the necessity of normalization according to conservation of charges ([3] , p. 106).
Niels Bohr’s steady state transition postulate, Heisenberg’s observable physical quantity thought, and Max Bohn’s probability interpretation of ψ function are Copenhagen School’s essence. Different from Newton-Eins- tein’s natural philosophy line, Copenhagen research line is “Steady state, transition, probability” ([4] , pp. 60-61). Einstein wrote in 1936: “ψ function can’t describe a single system in any way, but only can relate with many systems, the whole ensemble in statistical mechanics ([5] , p. 518).” Einstein and Karl Popper developed statistic ensemble interpretation of quantum mechanics.
Einstein had no hope to reform recent quantum mechanics in anti-probability ways. In the light of David Bohm’s quantum potential theory that try to interpret quantum mechanics in determinism ways, Einstein wrote a letter to Max Born: “You can see how David Bohm (in fact including De Broglie 25 years ago) has a belief to interpret quantum mechanics in another determinism ways? I regard this as a cheap inference, but of course you can have a better judgment.” “So far quantum statistical theory is still a consistent system, it describes rightly experimental relations between observable physical quantities and predicts its meaning in theory.” Einstein tried to regard quantum mechanics as a super-determinism restricted condition of future unified field theory in his exploration course ([2] , pp. 570-572).
2. Curvature Concept in Physics
The early developments of astronomy and mathematics involved in problems about circle and conic curve, ancient Greek astronomer and astrologer Ptolemy (310-230BC) had developed spherical astronomy, and people knew the difference between flat geometry and spherical geometry. But curvature concept and torsion concept didn’t enter into geometry until analytical geometry and non-Euclidean geometry arose.
Christian Huygens studied flat curve’s nature by pure geometrical method in Horologium Oscillatorium in 1673. Suppose a rigid normal in P point of a curve, when an adjacent normal approaches this rigid normal, their point of intersection attains limit position in the rigid normal direction, and this point of intersection is curvature center in P point of curve. Huygens proved that distance between P point and limit point of intersection was
 ; we call it curvature radius of P point in curve. Newton reached a similar conclusion in Geometria Analytica ([6] , pp. 301-302).
; we call it curvature radius of P point in curve. Newton reached a similar conclusion in Geometria Analytica ([6] , pp. 301-302).
Euler (1707-1783) used parameter equations x = x(s), y = y(s), z = z(s) to express a curve in space; s is arc length among them. According to spherical trigonometry, he obtained dx = pds, dy = qds, dz = rds from parameter equations, among them p, q and r are direction cosine varying along with points in curve, of course p2 + q2 + r2 = 1. Euler regarded differential of independent variable ds as a constant variable; he assumed that ds' was arc angle between adjacent tangent lines of two points of distance ds in curve. Euler defined ds'/ds as curvature radius of a curve.
Clairaut had advanced that a curve has two curvatures: one is Euler’s curvature definition; another is torsion that represents speed of a curve leaving from a plane in a point (x, y, z). Mathematician and engineer Michel- Ange Lancret (1774-1807) defined torsion concept by analysis method. He chose three main normal directions. The first main direction is direction of tangent line. Successive tangent lines are located in dense-tangent plane; the normal line in dense-tangent plane is main normal line, and its direction is the second mail normal line. The second normal line is vertical to dense-tangent plane; its direction is the third main direction. Torsion is the second normal direction’s changing speed relative to arc length. Lancret used equations x = ф(z), y = ψ(z) to represent a curve, and defined dμ as narrow angle between gradually normal planes, dν as narrow angle between gradually dense-tangent planes, so dμ/ds =1/r, dn/ds = 1/t, where ρ is curvature radius, and τ is torsion radius ([6] , pp. 303-307).
Playfair (1748-1819) expressed unproved parallel axiom anew in 1795: “There is one and only one parallel line in a point outside a straight line.” Russian mathematician N. I. Lobachevsky (1792-1856) published a paper “Brief introduction on a rigorous proof of parallel line axion” on February 23, 1826; he built a new virtual geometry where there are two or more parallel lines in a point outside a straight line. In this virtual geometry, space is not smooth but curved (the sum of angles of a tringles < π/2, circumference/diameter > π). After 1832, John Bolyai (1802-1860), Carl Friedrich Gauss (1777-1855) advanced similar viewpoints ([7] , pp. 258-259).
There is a normal line with a direction in each point (x, y, z) in curve. Gauss considered a unit spherical surface, and chose a radius with a direction of an oriented normal line in surface. The chosen radius determined a point (X, Y, Z) in spherical surface. If we considered a small region encircling point (x, y, z) in curved surface, then there is a corresponding region encircling point (X, Y, Z) in spherical surface. When this two regions shrink into their corresponding points, we defined the limit of rate of region area in spherical surface and region area in curved surface as curvature in point (x, y, z) in curved surface. Gauss obtained general curvature K of surface after astonishing differential calculus, and found that K is product of two main curvatures in point (x, y, z) of surface, this two main curvatures had been defined by Euler very early. Sophie German defined mean curvature of two main curvatures as mean curvature of surface in 1831 ([8] , pp. 301-303).
German mathematician Georg Bernhard Riemann (1826-1866) discussed curvature problem in n-dimensional manifold in his inaugural speech on June 10, 1854. Gauss’s intrinsic geometry of surface revised Pythagoras formula in 3-dimentional space, Riemann spread it in n-dimensional manifold. Riemann assumed the square of distance between two common points is , where gμν is a function of coordinates
, where gμν is a function of coordinates 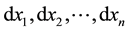 , and
, and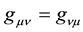 . The shortest line between two given points t = α and t = β is a geodesic what
. The shortest line between two given points t = α and t = β is a geodesic what
satisfies an equation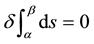 . Euclid presumed secretly that a vector is constant under parallel translation,
. Euclid presumed secretly that a vector is constant under parallel translation,
but Riemann gave up this secret hypothesis, and introduced a connection Г to represent deviation of vector direction under parallel translation, so curvature of a manifold may be constructed from connection Г ([8] , pp. 309-313).
In viewpoint of Riemann, physical space is a special manifold, we distinguish physical space from other manifolds only by experience. This train of thought led to relativity naturally ([8] , pp. 314-315). Along with applying differential geometry to physics, curvature concept had entered into Newton mechanics, Maxwell electromagnetism, relativity theory, thermodynamics, quantum mechanics and quantum field theory.
A curve in 3-dimentional Euclid space is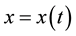 ,
,  ,
, 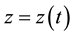 , so
, so  ,
,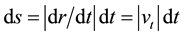 . Let t = s, the absolute value of acceleration relative to parameter s is curvature of curve in space:
. Let t = s, the absolute value of acceleration relative to parameter s is curvature of curve in space: , where speed vector is vertical to acceleration vector. So curvature concept entered into Newton mechanics by this differential geometry expression ([9] , p. 34).
, where speed vector is vertical to acceleration vector. So curvature concept entered into Newton mechanics by this differential geometry expression ([9] , p. 34).
The famous Gauss, Ampere, Faraday, Maxwell equations are
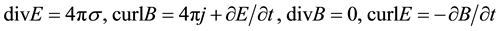
For handy purpose, we assume σ = 0, j = 0, so Maxwell equations are rewritten into differential geometry forms: dF = 0, d(*F) = 0,
where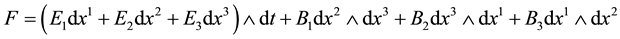 ,
, 
* is Hodge operator ([10] , pp. 118-119).
The second equation is in fact Bianchi identical equation in U(1) fibre bundle, where F corresponds to curvature 2-form field . Mathematicians including Cartan and Hodge noticed that Maxwell equations should be explained as curvature equations of some geometry objects of so-called vector bundles.
. Mathematicians including Cartan and Hodge noticed that Maxwell equations should be explained as curvature equations of some geometry objects of so-called vector bundles.
Maxwell equations led to special relativity naturally, Micheson-Morley experiment led to build light speed constant principle, H. Poincare advanced relativity principle. Einstein explained Lorentz transformation anew, and forced us to receive relativity of simultaneity, and led to H. Minkowski’s 4-dimentional space-time viewpoint. Under Lorentz transformation, an energy-momentum vector changes as a 4-vector. 4-momentum of a mass point locates in mass surface that has Lobachevsky geometry structure: 
General relativity extends relativity principle from an inertia system to a reference system of arbitrary motion. This means that physical laws keep invariance under an arbitrary space-time coordinates transformation, tensor differential calculus is the fittest tool to represent this general covariance. Einstein advanced equivalence principle according to Galilieo’s free falling body experiment in 1907: inertia mass was equal to gravitational mass, we described a physical phenomenon in an accelerating reference frame as same as it in a gravitational field. Generally, to be inertial in Einstein’s sense, the frame would refer to free fall under gravity, so that the Newtonian field of gravitational force would appear to have disappeared. We are to think of the world line of a particle, falling freely under gravity (Einsteinian inertial motion), as described as some kind of geodesic in curved spacetime: 
Began from Poisson equation of Newtonian gravity:

where G is Newtonian gravity constant, Rμν is Ricci curvature tensor, R is scalar curvature (R is the sum of each statistical weight of Rμν components, gμν as space-time metric isn’t only relative with curvature, but also with probability). John Wheeler pointed out that Einstein’s general relativity implied “space-time told matter how to move, matter told space-time how to curve”.
Later Einstein constructed some unified field models that regarded electromagnetic field as curved space-time structure: he followed Klein-Kaluza theory at the beginning, and treated electromagnetic field as the 5th extra dimension like super cylinder; finally he treated electromagnetic field as asymmetry tensors and joined it into symmetry gravity tensors. But along with enormous progresses and new problems in microphysics, Einstein’s unified field theory dream wasn’t realizable within the foreseeable future.
German mathematician Hermann Weyl advanced the gauge transformation concept in 1918. He tried to derive electromagnetism from invariance of physical laws under the transformation of measuring scale along each space-time point. At each point in space-time, the transformation of measuring scale is called as local gauge transformation. V. Fock and F. London found in 1927 that if we added an imaginary factor to scale factor in Weyl’s theory, then Weyl’s theory was no longer a gauge (scale) transformation theory, but then a phase factor transformation theory, and it described electromagnetism correctly. The phase choice of whole wave function is arbitrary in quantum mechanics. When the phase of a wave function changes, the observation value of mechanics quantity keeps invariance, the conservation quantity relative with this invariance is electric charge.
Gauge field theory is based in some symmetry principles, where the most important principle is local gauge invariance principle. Weyl proved that if we replaced common derivative with covariant derivative: 
According to Yang-Mills theory, if a group of physical laws satisfy global symmetry originally, when it spreads to local symmetry, a new field must be introduced to keep it invariant. Gauge field quanta is a new kind of particles whose exchange cause new force. On this ways, Yang-Mills theory gives a picture to describe the origin of various forces. Gauge potential plays a similar role in gauge field theory as gravitational potential in general relativity. Gravitational potential relates with linear connections in tangent bundles, reflects curvature in space-time bottom manifold; gauge potential relates with curvature in main fiber bundle, gauge potential reflects curvature of fiber bundles.
So gauge field has curvature like gravity field, for example, Yang-Mills field describes parallel displacements in electrical charge space, and determines curvature of electrical charge space. Under the Abel group U(1) situation, curvature tensor of electrical charge space is consistent with strength tensor of electromagnetic field, and then electromagnetic field has geometry structure ([11] , pp. 6-8).
When gauge theory hints the relation between curvature and quantum mechanics, we find that quantum curvature concept has already germinated from Erwin Schrodinger’s paper “Quantisierung als Eigenwent Problem”. In his “Four Lectures on Wave Mechanics”, Schrodinger thought that Hamilton-Maupertuis principle as classical starting point of wave mechanics introduced Heinrich Hertz’s generalized non-Euclidean line element


Geometrical optics is only coarse approximate optics, along with wave optics line, we should develop a new wave mechanics in q space. Perhaps our classical mechanics is similar to geometrical optics, as an error, it doesn’t conform to reality. Once curvature radius and route length can compare with a wavelength in q space, classical mechanics becomes invalid. So we seek to a new wave mechanics what starts from Hamilton similarity and find answers along with wave optics line ([3] , pp. 45-46).
As Max Bohn developed quantum probability interpretation from Schodinger’s weigh function of ψψ*, French mathematician Rene Thom developed quantum curvature interpretation from Schodinger’s non-Euclid q space, and advanced curvature interpretation about entropy in his works: “Structural Stability and Morphogenesis” (1972), “Mathematical Models of Morphogenesis” (1974). Guoqiu Zhao and some Chinese learned men made a complete systematic exposition on quantum curvature interpretation in their works: “Motion and Field” (1994), “New Divine Comedy of Physics” (2002), “Between Physics and Philosophy” (2007), “From Interactive Reality to Curvature Interpretation of Quantum Mechanics” (2008). Compared with other quantum mechanics interpretations, we find that quantum curvature interpretation is the easiest to concert with relativity, and it is the closest to Schodinger’s scientific thought and Einstein’s physics ideal until then.
Rene Thom considered two conservative Hamilton systems H1 and H2, and assumed that they were coupled in thermodynamics. Because of random interrelations, a system in energy hypersurface D domain was direct proportion to Liouville measure in D domain. The derivative a(x) = dm/dx represented (2m − 1) volume in energy hypersurface H = x, for two conservative systems, their volumes were a1(c − t) and a2(t) separately. Microcanonical entropy of a system was S(x) = lna(x), and its temperature was
According to Rene Thom’s viewpoint, there is a function according to normalized condition 
a hypersurface in Hilbert space, and it simplifies as total curvature of mapped graphics in no outside potential; There is a progressive increasing function q = h(e) in steady state form of Schrodinger equation 

Starting from guiding thought that ψ function reflects space-time features of micro-particles, Guoqiu-Zhao separates curvature factors from ψ function’s amplitude, curvature factors are called base curvature who stands for micro-particles’ space-time features:

In hydrogen atom, Louis de Broglie matter wave wavelength of electron on energy level n.







According to Heisenberg’s uncertainty relation, at each energy level in atom, the uncertain measurement ∆pn of electron’s momentum and ∆xn of the location will satisfy the following formula:
In discussing atomic electron, the electron’s momentum is generally regarded as electron’s momentum uncertain measurement, so

Known from uncertainty relation, the physical sense of ∆xn is the uncertain location of electron particle, the measurement of which exactly equals the electron’s curvature radius. And ψψ* is proportional to this curvature factor, so we can make a new interpretation for quantum wave function, this is quantum curvature interpretation ([13] , pp. 16-19).
Funding
General Research Project of Humanities and Social Science in Chinese Ministry of Education: “Ontology Research in Quantum Field Theory”, and its Serial Number: 12YJA720013.
Cite this paper
XinzhongWu, (2015) Probability and Curvature in Physics. Journal of Modern Physics,06,2191-2197. doi: 10.4236/jmp.2015.615222
References
- 1. Wu, D.Y. (1996) Wu-Dayou Collections of Scientific Philosophy. Social Science Literature Press, Beijing.
- 2. Pais, A. (1988) Subtle Is the Lord… Chinese Translation Version, Science and Technology Literature Press, Beijing.
- 3. Schrodinger, E. (2007) Lectures of Schrodinger. Chinese Translation Version, Peking University Press, Beijing.
- 4. Jin, S.N. (2007) Physics Base and Philosophy Background of Quantum Mechanics. Fudan University Press, Shanghai.
- 5. Jammer, M. (1989) The Philosophy of Quantum Mechanics. Chinese Translation, Commercial Press, Beijing.
- 6. Kline, M. (1979) Mathematical Thought from Ancient to Modern Times (2). Chinese Translation, Shanghai Science and Technology Press, Shanghai.
- 7. Jiang, X.Y. (2006) Fifteen Lectures about History of Science. Peking University Press, Beijing.
- 8. Kline, M. (1980) Mathematical Thought from Ancient to Modern Times (3). Chinese translation, Shanghai Science and Technology Press, Shanghai.
- 9. ДУбРОВИН, Б.А., HOBKOB, C.П. and ФOМеНKO, A.T. (2006) Modern Geometry (1). Chinese Translation, Higher Education Press, Beijing.
- 10. Liu, K.-F. and Ji, L.-Z. (2006) Mathematician Life of Shing-Tung Yau. Zhejiang University, Hangzhou.
- 11. Gui, Q.Q. and Gao, C. (2008) Philosophy Investigation on Gauge Field Theory. Science Press, Beijing.
- 12. Thom, R. (1992) Structural Stability and Morphogenesis. Chinese Translation, Sichuan Education Press, Chengdu.
- 13. Zhao, G.Q. (2008) From Interactive Reality to Curvature Interpretation of Quantum Mechanics. Wuhan Publishing House, Wuhan.


