Received 9 June 2015; accepted 27 September 2015; published 30 September 2015

ABSTRACT

When the electrically charged elementary particles of “normal” matter like protons and electrons mutually interact, their masses interact gravitationally and charge electrically. There is no interaction between the mass of one and charge of other particle. In this paper, we describe a prediction of the existence of a “pseudo-charge” of the same size as the common elementary electric charge, which seems to be possessed by neutrinos. If the prediction is relevant to the reality, the pseudo-charge interacts with the mass of normal particle in the interaction between this particle and neutrino. Consequently, the cross-section in a collision between neutrino and particle of normal matter is many orders of magnitude lower than that in the mutual collisions of normal-matter particles. However, the pseudo-charge of one neutrino interacts with the pseudo-charge of other neutrino in a mutual interaction of neutrinos and, consequently, their collisional cross-section is predicted to be again relatively large, essentially the same as that in, e.g., electron-electron collisions. We propose an experimental verification of the possible existence of neutrinic pseudo- charge with the help of two mutually crossing neutrino beams.

Keywords:

Maxwellian Electromagnetism, Maxwell Equations, Unified Theory, Elementary Particles, Neutrino

1. Introduction

Albert Einstein devoted many years of his scientific activities to a search for an unified description of four well-known interactions in the universe. From his era, this effort has continued till the present.

In the course of the unification, we achieved a certain progress, which was published in our two previous papers [1] [2] . It appeared that the classical theory of electro-magnetism by Maxwell [3] , completed with two formulas given into the quantum physics by de Broglie [4] [5] and with the concept of evanescent wave known from the classical physics, can describe the atom within the theory alone, without any addition of the principles of quantum physics. At the same time, the relevant solution of the Maxwell equations occurs to incorporate gravity, as the secondary electric force, as well as can explain the principle why the electric interaction increases about two or more orders of magnitude in the region near atomic nuclei in comparison to its Coulombian behavior (and is, thus, regarded as the strong interaction).

The concept of the interaction described by the solution also explains why the orientation of gravity must be the same as the orientation of primary electric force between the charges of opposite polarity, why the magnitude of the charge of all electrically charged elementary particles is the same, and why there is inertia linked to the mass of particles, but not to their electric charge.

The orientation of gravity with respect to the orientation of electric force between two charged particles was, basically, derived from the equation

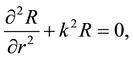(1)

where is the radial part of given component of the electric field intensity and k is the amplitude of wave vector. This equation is the differential equation of the second order. It can be decomposed to two differential equations of the first order using the unit and Pauli 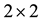matrices.

The quadrate 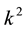of the magnitude of wave vector can be decomposed as 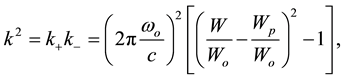[2]

(2)

where

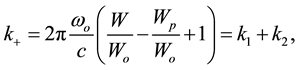(3)

(4)

with

(5)

In these equations, 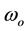is the rest angular frequency related to the rest mass of test particle, , according to the de Broglie relation 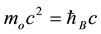(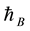is the Planck constant divided by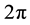), c is the speed of light, and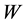, , 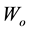and are the total, rest, and potential energy of the test particle in the force field of another particle, respectively.

If we establish operators

(6)

then Equation (1) ca be re-written to the matrix form

(7)

where, , and are three elements of the four-element set consisting of unit matrix and three Pauli matrices, is zero matrix and

(8)

Auxiliary parameter if is the unit matrix and if the latter is one of Pauli matrices.

Because we need only three matrices of the set of four to decompose Equation (1) and, moreover, there are a lot of combinations of the sequential order of these matrices, there is a plenty of possibilities for the decomposition, whereby each of these possibilities implies a specific kind of interaction between two considered particles. To describe the interaction between, in the given context, “normal” particles, as electrons or protons, one specific combination of all was used and this case is reminded in Section 2. Assuming the series of the com- binations with equal to unit matrix, we predict the corresponding orientation of the force between the particles for another set of combinations in Section 3.

Of the combinations listed in Section 3, we choose one interesting interaction and suppose that this interaction can be assigned to some hypothetical particles. The interesting feauture of the interaction is that the electric charge of particles possessing the relevant property does not interact with the electric charge of normal particles, but with their mass. So, we further refer to this special charge as “pseudo charge”, this interaction as to the “mixed interaction” and corresponding hypothetical particles as the “mixed-interaction particles” (M-IPs, here- inafter). We analyze some further basic properties of them in Section 4. Because these properties appear to be, at least qualitatively, identical to those, which are known for neutrinos, we identify the M-IPs to these tiny, weird particles and derive a consequence relevant to the dark matter in the universe.

An experimenal verification of the pseudo charge of neutrinos, if exists, is proposed in Section 5. We suppose that the experiment could be performed already at the present, using the technical facilities of the most advanced physical laboratories (particle accelerators) in the world.

2. Normal Electro-Gravitational Interaction

The Maxwell equations comprise a dependence on time. To eliminate this quantity in course to find a solution, the most obvious (if not unique) way is to assume the solution of the vectors of electric intensity and magnetic induction in the forms

(9)

(10)

respectively. In these forms, and are the vectors of the amplitudes of the intensity and induction, is the angular frequency of the wave associated with the considered particle (in our concept, the wave is permanently irradiated and absorbed by the particle; there is again valid de Broglie relation between the mass, m, of the particle and its angular frequency), i is the unit of imaginary numbers, and t is time.

In our new concept of the unified interaction, we do not regard the time solutions for and only as some mathematical forms of the solution, but physically interpret this result as follows. We will farther deal only with intensity vector, but the analogous deduction and representation can be done also for the induction vector. Since the vector of the intensity equals, we see that the electric field (i) must exist in the complex space, which has two sub-spaces, real-valued and imaginary-valued, (ii) in both sub-spaces the field harmonically appears and disappears, whereby changes its orientation from positive to negative and vice versa, and (iii) only its complex existence is constant (since its size is proportional to

).

Let us now consider an electrically charged particle, which generates the electric field in the surrounding space. The time dependences (9) and (10) are, however, valid wherever in the space. In every point, the vectors are harmically changing and, hence, they obviously represent the description of a spherical wave centred on the particle. There exists a possibility that this wave can deliver an impulse to another particle and, thus, accelerate it. However, the impulse must change its size and (what is important, in the given context) its orientation. Hence, the force action corresponding to such an interaction mechanism would result only in an oscillation of influenced object. No permanet action in a single direction, which is characteristic for the electrostatic force and gravity, could occur in this concept.

The permanent single-direction action occurs, in our concept, assuming the validity of old idea of screening one object by another, which was suggested by Le Sage in 1782. In more detail, he introduced the idea of fluid fulfilled with particles, which deliver an impulse to the objects randomly from all directions. A screening of one object by another disturbs the spherical symmetry of impulse delivered to a given object and, thus, the complete compensation of impulse delivered to this object. Since there is delivered a lower impulse from the direction of screening, the particle is accelerated in this direction due to the excess of impulse delivered from the opposite direction. However, while Le Sage applied his idea to the macroscopic bodies, we apply it to the “cores” of ele-

mentary particles. The size of the cores is gauged to be about, where is the

Planck length and is the common fine structure constant.

Our interaction mechanism is based on concept of permanently irradiated and absorbed wave by the considered test particle. When the wave is irradiated, it delivers a reaction impulse to the particle. If the returning wave impacts the particle, it simply delivers to it the carried impulse. Because of the perfect spherical symmetry of the outcoming and incoming waves, the impulse in a given direction is exactly compensated by the equal-size but oppositely oriented impulse from the opposite direction. Thus, the net impulse per time unit, i.e. the force, is zero.

The test particle is accelerated when the symmetry is disturbed. In analogy with the Le Sage’s concept, it can happen by screening of the impacting wave by another particle(s) or when the test particle is forced to accelerate and the symmetry is then broken due to the blue shift and red shift of the parts of wave in the direction of acceleration and in opposite direction, respectively. The first reason leads to the force laws and the second one to the law of inertia.

In our concept of interaction, every elementary particle is regarded as a source of waving. The amplitude of generated spherical wave increases with the decreasing radial distance from the particle, down to a certain critical distance, where the existence of wave reaches so high measure that the wave is able to absorb the wave of other particle. We assume that the absorption is proportional to the wave amplitude, which corresponds, in the case of static interaction, to the amplitude of the electric intensity, in the critical distance. Thus, the absorption ability, i.e. the effective absorption cross-section in fact, can be derived from the electric intensity in the critical distance. Since the intensity has both real-valued and imaginary-valued components, there are obviously the absorbing agents in both the real sub-space and in the imaginary sub-space. Each of these agents has its specific, real-valued or imaginary-valued, cross-section.

In physics, the quantities acquiring the imaginary values are regarded as unobservable and, usually, are ignored in the interval, where their values has non-zero imaginary component. In our concept, the imaginary part of the wave generated by the test particle in the position of an absorbing particle is absorbed by the agent in the imaginary sub-space. Mathematically, the corresponding force due to the absorption is proportional to the product of imaginary part of the electric intensity and imaginary cross-section. This product of two imaginary values is however real-valued and, therefore, observable in the real world. In this way also the imaginary parts of physical quantities appear to be observable.

In our earlier papers [1] [2] , we reached a success to incorporate gravity into the solution of the Maxwell equations for two static, electrically charged particles (or two static, point-like objects consisting of such particles), when we tried to find the solution for the vector of the amplitude of electric intensity describing the force field of test particle in the form

(11)

(12)

(13)

Function in relation (11) appeared to be constant. The r-dependent part of the radial component, , was found to equal

(14)

where is an integration constant.

In Equation (14), the r-dependent part of the first term of -component of the intensity was determined by equation

(15)

which is formally identical to Equation (1) and, thus, it can be decomposed and solved in the same manner as the latter.

Let us denote the Pauli matrices as

(16)

We remind the properties of these matrices: for (, 2, and 3 as well as, 2, and 3; is zero matrix) and (is unit matrix). Just these properties enable the re-writting of Equation (1) to Equation (7), i.e. the decomposition of Equation (1).

To obtain the solution for the normal-matter particles interacting in the common way, we put, , and in the decomposition of equation (7), when solving Equation (15). Consequently, we obtained

(17)

(18)

where was an integration constant. Using this result and Equation (14), two variants of r-dependent part of the radial component are

(19)

(20)

We denoted.

The total energy of particle with the rest angular frequency equals

(21)

In the hydrogen atom as well as in the macroscopic regime of unified interaction, energy is the Coulomb potential energy, which can be written with the help of so-called “elementary electromass”, , as

(22)

for two oppositely charged elementary particles. is the elementary electric charge (charge of proton), is the permittivity of vacuum, and G is the gravitational constant. In the case of potential energy (22), the ratio can be given with the help of so-called “electric radius”, , as, whereby. In fact, the electric radius is an electric analogue of the Schwarzschild gravitational radius.

Subsequently, the relations (5) giving the terms of wave vector and can be re-written as

(23)

(24)

where we utilized de Broglie relation to write in the original relations as. The magnitude of wave vector can be given as

(25)

As we mentioned above, the wave gains the ability of the effective absorption of other wave in some very small radial distance from the particle, which we denote by and refer to (in consistency with our previous papers) as “interaction radius”. It appeared that the exact form of the Newton force law and, at the same time, Coulomb law can be reproduced by gauging the ratio to equal the ratio. Hence

(26)

In the distance, the size of the wave vector, k, and size of its part reduce to

(27)

(28)

Part, which does not depend on distance, remains given by relation (24). Since for the common

elementary particles (as seen in relation (28)), we neglect in the calculation of k as well as

and (see relations (3) and (4)).

The argument of functions sine and cosine, kr, in relations (19) and (20) equals the ratio in. Hence, and. Since the rest mass of common elementary particles is many orders of magnitude lower than the elementary electromass, i.e., we can approximate, with a high precision, and.

Using all expressions for the distance, the r-dependent parts of the radial component of electric intensity, which are originally given by relations (19) and (20), can be re-written to

(29)

(30)

These relations characterize the absorption ability of the charged particle with rest mass. Specifically, the size of the absorption in the real-valued sub-space is about the factor of times lower than that in the imaginary-valued sub-space. To obtain the conventional Newton and Coulomb laws, we can choose the constant in such a manner that the absorption measure in the real-subspace becomes and that in the imaginary-valued subspace. The former can be related to the gravitational mass and the later is an equivalent of the electric charge. It is reasonable to consider not only the quantity, but also its complex conjugate. Thus, we have the equivalents and of both positive and negative elementary electric charges, respectively.

In distance r, the total surface area of the spherical wave is. If the absorption cross-section is, then part of the whole wave is absorbed. The proportionality is respected in the denominator of the fraction in relation (11). In our paper [1] we derived the conclusion that the macroscopic interaction is the regime of force occurring in the distances. In this regime, the variants of functions and are given by relations (29) and (30) and the corresponding variants of the amplitude of electric intensity (according to (11)) are

(31)

(32)

with the plus for the positive and minus for the negative charge in the last relation. It appeared that the components and are negligible with respect to for.

The variants of force corresponding to and given by relations (31) and (32) can be calculated as the product of real-valued absorption agent and real-valued form of the intensity amplitude, i.e., as well as as the product of imaginary-valued agent (if the wave of test particle is absorbed by other positively charged particle) or (if it is absorbed by other negatively charged particle) and imaginary-valued form of the intensity amplitude, i.e.. Specifically, there is considered with sign plus if the charge of test particle is positive and with sign minus if this charge is negative.

While product of real-valued quantities determines the properties of gravity, prod-

uct is relevant to the elecrostatic force. We can check that the ratio of both products, , actually equals the ratio of Newton gravitational and Coulomb electrostatic force laws. For the interaction between two protons with, ratio, i.e. the ratio of the magnitudes of gravity and electric force. The determination of constant and giving the exact forms of the Newton and Coulomb laws is not trivial, therefore we do not repeat here its derivation. It was derived in our earlier paper [1] .

We can see that product related to the electric interaction between two charges of the same polarity is negative and product

related to the electric interaction between two charges of opposite polarity is positive. As well, product related to the gravitational interaction is positive. Hence, the orientation of gravity must be the same as the orientation of the electric force between two charges of opposite polarity.

In contrast to B-variant, the amplitude of the A-variant of intensity, , can be also given in the form containing the angular frequency. If the object accelerates, this frequency is blue- shifted in the direction of acceleration and red-shifted in the opposite direction. The symmetry of the emitted and absorbed wave is broken and the asymmetry causes the inertia force. Because the primary electric term, given by variant B, does not depend on the frequency, there cannot be any blue or red shift and, consequently, the electricity does not possess any inertia.

3. The First Complete Series of Dirac-Type Decomposition

To describe the common, well-known interaction between the paticles of normal matter in Section 2, we considered one specific combination of matrices, , and when solving Equation (15) via the Dirac-type decomposition of this second-order differential equation. The decomposition is demonstrated with the general Equation (7). In this section, we briefly review the decompositions with and all possible pairs composed of three Pauli matrices, which are supplied into and. (The decomposition requires, therefore the pairs consisting of the same and matrices are impossible.)

If, then in Equation (7), whereby this equation is obeyed when either its first or the second factor equals zero matrix. Or, this implication can be written as single equation with ± signs:

(33)

Solving this matrix equation, we obtain two variants, and, of the solution for the radial part of - component of the vector of electric intensity. Using further relation (14) and denoting, we can calculate the corresponding radial parts, and, of the radial component of the intensity, and finally, using relation (11), two variants of the amplitude of the radial component of electric-intensity vector, and.

It appears that the A-variant is the same for all studied combinations and equals

(34)

for regardless we consider sign plus or minus in Equation (33). We remind that condition determines one series of stable static positions of electron in the force field of proton in the hydrogen atom [1] [2] . The macroscopic regime appears if there is valid. (In atom, , but in the potential of the Earth.) Thus, the form of the radial component of the intensity amplitude can be approximated as

(35)

in the case of variant A.

As already explained in Section 2, the force action of an acting particle on a test particle depends on the intensity of the test particle and, therefore, on its amplitude, actually given by relation (35) in the A-variant. And, the force action depends on the absorption rate, the factor of which can be derived applying relation (35) to the acting particle in the distance from it. To obtain the conventional proportionality to the particle’s mass (in gravitational interaction) or to the electromass, which is the equivalent of electric charge (in electric interaction), we gauge the integration constant to become

(36)

Then Equation (35) in yields the absorption factor.

For variant B, i.e. for, the result is listed in Table 1. The first column of this table gives the serial number of given combination. The second column specifies the unit matrix and Pauli matrices supplied for, , and in Equation (33). The third column gives the general solution for the region of radial distances, fourth column the form of this solution in, and the last column the absorption factor, , derived from this solution and applied on the acting particle in the distance from it equal to. And, constant was, again, gauged according to relation (36).

Let us now describe the possible kinds of macroscopic-type interaction with the help of corresponding force, which is the product of the intensity amplitude (relation (35) in the case of A-variant or the form given in the fourth column of Table 1 in the case of B-variant) and absorption factor, i.e. in the case of A-variant, or (the fifth column of Table 1) in the case of B-variant. In the description, we distinguish between the rest mass of the acting and rest mass of test particles.

Within variant A, there is only the force, which is proportional to. As already mentioned, in Section 2, it is the secondary electric force identified to gravity between the particles of normal matter.

Concerning variant B, it appears that this part of force corresponds to the common primary electric force or another, newly predicted, kinds of force. Among the found combinations, the primary-electric interaction between two particles of normal matter is described by forms, which are listed as No. 4 in Table 1, 4th and 5th column. One can see that this force is proportional to.

The solutions of B-variant Nos. 3 and 5 in Table 1 yield a weird interaction related to a particle of hypothetical kind. If we consider the interaction bewtween this particle and “normal-matter” particle, then the corresponding force is predicted to be not unique in the following sense. When the test particle is the hypothetical particle and acting particle is a particle of normal matter, the force on the test particle is proportional to. In contrast to this, if the test particle is a normal-matter particle and acting particle is the hypothetical particle, then the force on acting partcle is proportional to. In other words, the force acting on the hypothetical particle is proportional to the first form given above and that acting on the normal-matter particle is proportional to the second above form. Both forces are identical only for the particles of equal masses, i.e..

Because of two signs in front of both above-given forms, each force, on the hypothetical as well as normal- matter particle, can be as repulsive as attractive. If we consider this kind of force between a proton as the test particle and the hypothetical particle with the rest mass again equal to the rest mass of proton, , then the size of the (equal) force is times stronger than gravity and

of the size of electrostatic force between two protons.

As stated in Section 2, the inertia force occurs due to an acceleration of particle causing a blue shift and red shift of emitted and absorbed wave. Hence, the force depends on the angular frequency of the wave. The intensity linked to the solution of B-variant No. 3 and 5 is reciprocally proportional the square root of mass and, hence, the angular frequency of the wave associated with the particle. Thus, we could expect a dependence of inertia force of this particle on the B-variant of solution for the radial part of the intensity. However, the corresponding integral to calculate the inertia force equals exactly zero, therefore the inertia force is, also here, generated only by the mass-linked term of A-variant (see [1] ). In other words, the inertia force is the same as in the case of “normal-matter” particles.

The solution of B-variant No. 2 in Table 1 is similar to the solution No.4 for the normal matter except of the orientation of corresponding force. As in the case of normal matter as in that between the hypothetical particles possessing this interaction, the force between the charges of the same (opposite) polarity is repulsive (attractive). However, if the hypothetical particle of this kind interacts with a charged particle of normal matter, then the force is attractive (repulsive) if the polarity of charges is the same (opposite). It is rather hard task to imagine an universe with the particles having this strange charge.

Finally, there are the solutions of B-variant Nos. 1 and 6, which are practically identical in respect to the macroscopic-interaction properties, in Table 1, the fourth and fifth columns. Some fundamental properties of the particles possessing this kind of interaction are analyzed and discussed in two next sections.

4. Solution for “Mixed Interaction”. Neutrino as Pseudo-Electrically Charged Particle and Possible Relationship to Dark Matter

In this section, let us consider the solution of B-variant No. 6 (Table 1) of the amplitude of electric-field intensity. In the region of distances, the size of this amplitude equals to its counterpart for normal matter, but it is the real-valued quantitity. Therefore, the corresponding electric force between a hypothetical particle possessing this kind of interaction and particle of normal matter is proportional to (is the rest mass of normal-matter particle). Below, we demonstrate that the hypothetical particles possessing the interaction corresponding to the solution of B-variant No. 6 of the electric-intensity amplitude are the M-IPs mentioned in Section 1.

In other words, while the force between two particles of normal matter is the product of (i) real-valued mass and real-valued A-variant of the intensity amplitude (i.e. the product of mass and mass in fact) or (ii) imaginary-valued electromass and imaginary-valued B-variant of the intensity amplitude (i.e. the product of charge and charge), the force between the M-IP and particle of normal matter is the product of real-valued mass of normal-matter particle and real-valued B-variant of the intensity amplitude, i.e. the product of mass and charge in fact. (The last description is related to the situation when the M-IP is test particle on which the normal-matter particles acts. When we regard the normal-matter particle as the test particle on which the M-IP acts, then the force is product of real-valued electromass and real-valued A-variant of the intensity amplitude. The result of the multiplication is the same and equals.)

We note, there is also the common gravitational interaction between the M-IP and normal-matter particle. Its magnitude is, however, expected to be many orders of magnitude lower than the magnitude of the force described above. (The ratio of the magnitudes of both forces cannot be specified numerically, since we do not know the size of the rest mass of M-IP.)

We see that the M-IPs are predicted to possess an electric charge, which however does not interact with the charge of normal-matter particles, but with the mass of the latter. This peculiar property was the reason of why we established, in Section 1, referring to this charge as “psedo-charge” to distinguish it from the common electric charge.

Because the solution of B-variant No. 6 contains both signs, plus and minus, the force between the M-IP and particle of normal matter can be as repulsive as attractive. So the force between two M-IPs. In contrast to normal, primary-electric force, the orientation of force between two M-IPs with pseudo-charges of the same (opposite) polarities is attractive (repulsive), however.

As stated in Section 2, the inertia occurs due to asymmetry of the spherical wave caused by an accelerated motion. In the direction of the acceleration (in the opposite direction), the wave is blue-shifted (red-shifted) and, therefore, its frequency increases (decreases) and, thus, the carried impulse is enlarged (reduced). The shift of the wavelength can, however, appear only if the formula describing the wave, which corresponds to the amplitude of the electric-field intensity, contains the frequency or angular frequency.

One can see that while the solution of A-variant is proportional to mass and, hence, to the angular frequency, which is related to the mass according to the de Broglie’s formula, the solution of B-variant, as No. 4 for normal matter as No. 6 for M-IPs, does not contain mass. Therefore, there is no wave shift and, consequently, there is no inertia of either the normal electric charge or pseudo-charge. The inertia force of M-IP is related only to its mass and relatively low amplitude of A-variant solution.

Let us now estimate the collisional cross-section, when the M-IPs collide with the electrically charged elementary particles of normal matter. At the collision, the kinetic energy of incident M-IPs is and we assume this energy to be so high that the Rutherford formula for the calculation of the cross-section is relevant. According to this formula, the mean cross-section can be calculated as

(37)

where is the mean value of function in the interval of scattering angle from 0 to, and and are the charges of incident and target particles, respectively. With the help of elementary electromass, , relation (37) can be re-written to the form

(38)

Z_i and Z_t are the ionization degrees of the incident and target particles, respectively. Since we consider charged elemenary particles,.

The size of the pseudo-charge is the same as the size of elementary electric charge. Hence, factor in relation (38) remains to be conserved in the formula giving the cross-section, when the collision of M-IPs and normal-matter particles is considered. However, factor must be replaced with factor, because the pseudo-charge of M-IP interacts with this mass. For the mean collisional cross-section of M-IPs-normal-matter particles, , we thus obtain

(39)

One can immediately reveal that this cross-section is extremely small. For example, it is about the factor of times lower in the case of collisions between the M-IPs and protons than the cross- section in the proton-proton collisions. Since the extremely small cross-section is the property known at neutrinos, it is reasonable to identify, at least hypothetically, M-IPs to the latter.

Because neutrinos have an extremely small (inertial) mass, if any finite, their effects on the particles of normal matter are negligible regardless they possess or do not possess the pseudo-charge. Even if these particles have the pseudo-charge, they remain hardly detectable. An exception, which can be utilized in an experimental detection of pseudo-charge, is discussed in Section 5.

Of course, the consequence of the pseudo-charge, if exists, on the structure of the universe would be significant. Neutrinos usually have a large kinetic energy per unit mass, therefore they are deliberated from various bounds with the other particles, among themselves, or with the macroscopic objects. The exception can, however, be expected in the case of compact objects, like those residing in the centers of galaxies and quasars. The extremly strong gravity of these objects can obviously trap the neutrinos tending to pass through them or in their close vicinity. If we do a thinking experiment in which we want to move with such the trapped neutrinos, their motion is possible, due to the strong bounding, only if we move the whole object. So, the bound neutrinos acquire the inertia of the compact object and they then behave, with this “borrowed” inertia, as the particles with the mass equal to.

The interstellar and intergalactic space, as well as the space among the clusters of galaxies is likely fulfilled with a “neutrino pseudo-plasma”. (We identify the pseudo-plasma to a gas consisting of ionized particles possessing the pseudo-charge.) We assume the plasma instead some bound neutrinic structures because of the large kinetic energy of neutrinos per unit mass. The large energy means that the neutrino “soup” is hot and, hence, in the form of the pseudo-plasma.

Because of the neutrinos trapped inside the compact objects, the homogenity of the pseudo-plasma in the universe is obviously disturbed. In a smaller or larger region around every compact object, there is probably a relatively larger concentration of neutrinos with the positive sign of pseudo-charge (this pseudo-charge attracts the normal matter). On contrary, a relatively larger concentration of negative pseudo-charge neutrinos can be expected especially in the space among the galaxy clusters, if we believe that the total pseudo-charge of the universe is zero.

5. Suggestion of Experimental Verification of Potential Electric Pseudo-Charge of Neutrinos

As we mentioned above, the dominant interaction between the particles of normal matter and neutrinos, when the latter are identified to the M-IPs, is that between the mass of former and pseudo-charge of the latter. In the interaction between two neutrinos/M-IPs, the dominant interaction must be, however, that between their pseudo-charges, since the product of pseudo-charge, or, and the intensity in the region of distances proportional to or (according to Table 1) is real-valued.

Since the magnitude of the elementary pseudo-cherge is the same as the magnitude of elementary electric charge, the magnitude of elementary pseudo-charge-with-pseudo-charge interaction is exactly equal to the magnitude of elementary charge-with-charge interaction. Hence, the collisional cross-section in the mutual collisions between neutrinos/M-IPs is again given by relation (38) with (not by (39)) and is essentially the same as that in, e.g., electron-electron collisions, if the equal energy of incident particles is assumed.

Because of this “normal” size of the collisional cross-section, a significant fraction of neutrinos in a collimated beam should be effectively dispersed by another neutrino beam, which crosses the first beam. The measured flux of neutrinos should detectably change in dependence on whether the crossing beam is switched on or off. This is the principle to experimentally reveal the eventual existence of the pseudo-charge of neutrinos.

At the experiment, one has to be aware of the possibility that there are three types of neutrinos, electron, muon, and tau, and not all may possess the pseudo-charge. This situation can be analogous as that with, e.g., nucleons or pions, some of which are electrically neutral.

6. Summary

Our analysis of the potential kinds of interaction, based essentially on the Maxwellian electromagnetism, predicts an existence of elementary particles possessing a pseudo-charge with the size equal to that of common elementary electric charge, which however does not interact with the charge of normal particles, but with the mass of the latter.

In a collision of such a hypothetical particle with a particle of “normal” matter, as proton or electron, the collisional cross-section is many orders of magnitude smaller than that in, e.g., proton-proton collision. (At low incident energies, the cross-section in the hypothetical particle to proton collision is about 36 orders of magnitude smaller than the cross-section in the proton to proton collision.) Because of this property, we suggest to identify these hypothetical, pseudo-charge possessing, particles to neutrinos.

In the mutual collisions of the hypothetical particles/neutrinos, the pseudo-charge of incident particle is predicted to interact with the pseudo-charge of target particle. So, we have the pseudo-charge-with-pseudo-charge interaction, which is analogous to the charge-with-charge interaction in, e.g., proton-proton or electron-electron collisions. Hence, the neutrino-neutrino collisional cross-section, if neutrino actually possesses the pseudo-charge, is relatively large, essentially the same as that in, e.g., electron-electron collisions (assuming that the incident particles have the same energy, of course).

If the neutrino-neutrino collisional cross-section is as large as predicted (like that of “normal” charged particles in their mutual collisions), it can be verified in an experimental way, most probably using the current facilities, or facilities which can be constructed using the currently available technologies. Namely, we are able to measure a flux of neutrinos in a beam. If this beam is crossed by neutrinos emitted in other beam, the latter should significantly disperse the neutrinos in the former beam and a decrease of the flux would reveal the existence of the neutrinic pseudo-charge.

Acknowledgements

The work was supported, in part, by the VEGA―the Slovak Grant Agency for Science, grant No. 2/0031/14, and by the Slovak Research and Development Agency under the contract No. APVV-0158-11.

Cite this paper

LubošNeslušan, (2015) Neutrinos as the Particles with Mixed Interaction and Prediction of Large Neutrino-Neutrino Collisional Cross-Section. Journal of Modern Physics,06,1756-1767. doi: 10.4236/jmp.2015.612177

References