Journal of Modern Physics
Vol.06 No.08(2015), Article ID:57963,6 pages
10.4236/jmp.2015.68109
Boltzmann or Gibbs Entropy? Thermostatistics of Two Models with Few Particles
Enrique N. Miranda1,2
1IANIGLA, CONICET, CCT-Mendoza, Mendoza, Argentina
2FCEN, Universidad Nacional de Cuyo, Mendoza, Argentina
Email: emiranda@mendoza-conicet.gov.ar
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2015; accepted 12 July 2015; published 15 July 2015
ABSTRACT
We study the statistical mechanics of small clusters (N ~ 10 - 100) for two-level systems and harmonic oscillators. Both Boltzmann’s and Gibbs’s definitions of entropy are used. The properties of the studied systems are evaluated numerically but exactly; this means that Stirling’s approximation was not used in the calculation and that the discrete nature of energy was taken into account. Results show that, for the two-level system, using Gibbs entropy prevents temperatures from assuming negative values; however, they reach very high values that are not plausible in physical terms. In the case of harmonic oscillators, there are no significant differences when using either definition of entropy. Both systems show that for N = 100 the exact results evaluated with statistical mechanics coincide with those found in the thermodynamic limit. This suggests that thermodynamics can be applied to systems as small as these.
Keywords:
Entropy, Boltzmann, Gibbs, Few-Particle Systems

1. Introduction
There is currently a controversy regarding which is the correct definition of entropy at microscopic level, with Boltzmann’s traditional definition on one side and Gibbs entropy on the other. At the same time, there is a debate on the validity of traditional thermodynamics applied to few-particle systems. This note addresses these two issues from a numeric point of view for two very well-known and useful systems in all areas of physics: the two- level system and the harmonic oscillator. Even if the conclusions do not have the general validity they would, coming from completely theoretical arguments, they still shed light on the matter. Besides, as these are “ubiquitous systems”, the results obtained are relevant to several areas of physics, and they are of particular interest in the study of nanoclusters.
Boltzmann’s traditional definition [1] [2] states that, at microscopic level, entropy is:
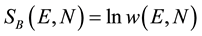 (1)
(1)
w(E,N) is the number of available microstates for a system with N particles and energy E. The result obtained from this equation is known as Boltzmann or surface entropy.
The definition given by Gibbs [3] leads to the so-called volume entropy and is expressed:
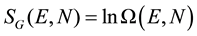 (2)
(2)
Ω(E) is the number of microstates available to the system with energy ε ≤ E. Both definitions are clearly connected:
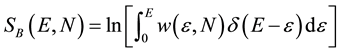 (3a)
(3a)
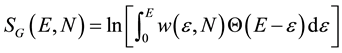 (3b)
(3b)
Recently, the validity of SB has been challenged and it has been argued that the correct definition is SG [4] - [10] . In the past months, a paper by Dunkel and Hilbert (DH) [11] has intensified this debate, and it has received interesting critiques [12] [13] that have been answered by Hilbert, Hänggi and Dunkel [14] . At the same time, there is a disagreement on whether thermodynamics is only valid for macroscopic systems [12] [13] or if it can also be applied to few-particle systems [11] [14] . Arguments in favor of each position are rigorous and general, and the discussion can be expected to go on for some time. In this note, we analyze both issues for the two- level system and for a cluster of oscillators. The work is numerical but exact, with no approximations.
Since the aim is to analyze systems with very few particles (N ~ 10 - 100), it is necessary to follow the microcanonical formalism, where the energy is constant since the system is assumed to be isolated. It cannot be assumed that the system is connected to a thermal reservoir because, given the small size of the system, their interaction would be of such relative magnitude that the system would be constantly out of equilibrium. Also, with these sizes it is not possible to ignore the discrete nature of energy: the system has M, M + 1, M + 2, ...energy quanta so that energy cannot be considered a continuous variable and, consequently, we cannot speak of derivatives but of finite differences. To this effect, the traditional equations of thermodynamics must be modified, thus:
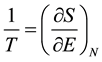 (4a)
(4a)
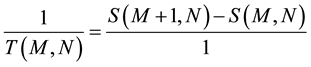 (4b)
(4b)
It is important to note that (4b) is not an approximation of (4a) but represents the actual situation. When a system has a large number of quanta, E can be considered a continuous variable and can be derived without difficulty, but for the case of very few-particle systems it is inevitable to take into account the discrete nature of energy. The same happens with the specific heat C:
 (5a)
(5a)
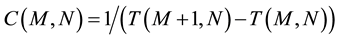 (5b)
(5b)
To begin with, we could define a forward temperature and specific heat, and a backward temperature and specific heat for a state with M energy quanta, and these forward or backward quantities will depend on whether this state is being compared with a state that has (M + 1) or (M − 1) quanta. It is better to calculate finite differences forward so that the quantities are well defined when the system has zero energy; otherwise, we should evaluate the number of states with (−1) or (−2) quanta, which is absurd. On the other hand, for N ~ 100 there is no difference between the results obtained in either way.
2. Results
Now we can proceed to calculate exactly the entropy, temperature and specific heat that can be obtained from the definitions by Boltzmann and Gibbs, and using (4b) and (5b).
It is well known [1] that the number of microstates in a two-level system with N elements and M energy quanta is:
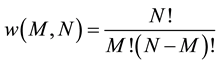 (6)
(6)
Therefore, the entropies by Boltzmann and Gibbs for this system are:
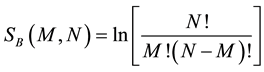 (7a)
(7a)
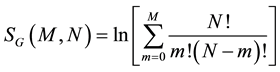 (7b)
(7b)
From (7a) and (7b), and using (4b) and (5b) the temperature and specific heat can be obtained exactly, that is, without applying the Stirling’s formula since it has be noticed that this approximation should be avoided for finite systems [15] - [17] . The results are shown in Figure 1 for N = 10, and in Figure 2 for N = 100. Subscripts B (G) refer to the parameters calculated with Boltzmann (Gibbs) entropy. It is important to note that the values depicted with symbols are the only ones where the parameters in question are defined; the solid line is just a visual aid. The specific heat also includes the result for the thermodynamic limit evaluated at the points of interest.
Figure 1 yields some interesting conclusions. As DH state, the use of Gibbs entropy avoids the occurrence of negative temperatures; however, the price to pay is that for M/N > 0.5 the temperature TG increases very rapidly. Figure 1(b) shows that Boltzmann temperature TB is in the interval (−6, 6) and does not diverge because the system is finite. On the contrary, Gibbs temperature assumes very high values: for E = 0.8 it is TG = 102 and for E = 0.9 it is TG = 1023. This is caused by the plateau shown by SG for those energy values, which occurs because the number of microstates available to the system for those energy levels increases at a very slow pace. DH’s arguments to choose SG over SB are theoretical and general, whereas the results presented here, though only valid for two-level systems, show that using SG leads to physically strange results.
Figure 2 shows the entropy, temperature and specific heat for N = 100. The behavior of both the entropies and temperatures are analogous to the previous case. Again, Gibb temperature assumes unphysical values for high energy levels: for E = 0.8 it has TG = 109 and for E = 0.9 it is TG =1015. As in the previous case, TB does not diverge because the system has a finite size. As regards the specific heat, the result obtained using SB is indistinguishable from that obtained in the thermodynamic limit. This suggests that traditional thermodynamics is valid for a system with a size in the order of 102.
The previous calculations are repeated for a cluster of N harmonic oscillators. In this case, it is known [1] that the number of microstates for a system with M energy quanta is:
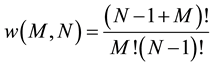 (8)
(8)
Boltzmann and Gibbs entropies can be expressed like (7a) and (7b), and next it is possible to calculate the entropies, temperatures and specific heats. The results for N = 10 are shown in Figure 3. The entropies SB and SG behave similarly, and the same happens with the temperatures TB and TG. As regards the specific heat, the value found in the thermodynamic limit has also been included and it can be seen that, for a size as small as this, CG is already indistinguishable from the thermodynamic specific heat Cthermo for high energies. The behavior of CB is qualitatively similar but the asymptotic value is slightly lower than Cthermo. For N = 100 the calculated quantities give the same results whether they are evaluated for a finite system using exact values of SB and SG, or the usual result in the thermodynamic limit. Once again, this result seems to suggest that for N ~ 102 traditional thermodynamics yields correct values.



Figure 1. Exact numerical results are shown for the two-level system with N = 10 and a variable number of energy quanta M. For such small systems the discrete nature of energy cannot be ignored and, therefore, the different parameters make sense only in the values corresponding to an integer number of quanta; the dotted lines are only a visual aid. All the parameters are plotted in relation to the energy per particle E = M/N: (a) Boltzmann entropy SB (●) and Gibbs entropy SG (□); (b) Boltzmann temperature TB (●) calculated with SB, and Gibbs temperature TG (□) with SG; and (c) the specific heat from Boltzmann CB (●) and Gibbs CG (□). The specific heat Cthermo (▲) obtained in the thermodynamic limit is also included.



Figure 2. Results for the two-level system with N = 100 are shown in relation to the energy per particle E: (a) entropies SB (●) and SG (□); (b) temperatures TB (●) and TG (□); and (c) specific heats CB (●) and CG (□). The specific heat calculated exactly using Boltzmann entropy coincides with that found in the thermodynamic limit Cthermo (▲).



Figure 3. Results for a system with N = 10 harmonic oscillators: (a) entropies SB (●) and SG (□) in relation to the energy; (b) temperatures TB (●) y TG (□) in terms of E; and (c) specific heats CB (●), CG (□) and the usual thermodynamic Cthermo (▲). For N = 100, the results obtained after evaluating the system exactly with the two entropies are indistinguishable from those found in the thermodynamic limit.
3. Conclusions
To sum up, the thermodynamic properties of two-level systems and harmonic oscillators with clusters of N = 10 and N = 100 have been calculated numerically but exactly. Given the small number of particles, it is necessary to take into account the discrete nature of the energy, which means replacing derivatives for finite differences. This is important for the smaller systems (N = 10) but it is irrelevant for the larger systems (N = 100). As regards the use of Gibbs entropy instead of Boltzmann’s, for the oscillators there is no difference, whereas for the two-level systems it means that the temperature does not assume negative values but such values are very high, which is physically implausible. The suggestion by DH regarding the replacement of Bolzamann by Gibss entropy is not supported by our results.
Acknowledgements
We have already published, for educational purposes, some preliminary results of this work [18] , and at the moment we are analyzing the case of few fermions/bosons systems. Financial support from Universidad Nacional de Cuyo through Proyecto SeCTyP 06/M072 is acknowledged.
Cite this paper
Enrique N.Miranda,11, (2015) Boltzmann or Gibbs Entropy?
Thermostatistics of Two Models with Few Particles. Journal of Modern Physics,06,1051-1057. doi: 10.4236/jmp.2015.68109
References
- 1. Callen, H.B. (1985) Thermodynamics and an Introduction to Thermostatistics. Wiley, New York.
- 2. Kinchin, A.I. (1949) Mathematical Foundations of Statistical Mechanics. Dover, New York.
- 3. Gibbs, J.W. (1902) Elementary Principles of Statistical Mechanics. Yale University Press, New Haven. (Reprinted by Dover, New York, 1960)
- 4. Campisi, M. (2005) Studies in History and Philosophy of Science Part B, 36, 275-290.
http://dx.doi.org/10.1016/j.shpsb.2005.01.001 - 5. Campisi, M. (2007) Physica A, 385, 501-517. http://dx.doi.org/10.1016/j.physa.2007.07.004
- 6. Campisi, M. (2008) Studies in History and Philosophy of Science Part B, 39, 181-194.
http://dx.doi.org/10.1016/j.shpsb.2007.09.002 - 7. Campisi, M., Zhan, F., Talkner, P. and Hänggi, P. (2012) Physical Review Letters, 108, Article ID: 250601. http://dx.doi.org/10.1103/PhysRevLett.108.250601
- 8. Campisi, M. (2007) Microcanonical Phase Transitions in Small Systems. arXiv: 0709.1082v1 [cond-mat.stat.mech].
- 9. Dunkel, J. and Hilbert, S. (2006) Physica A, 370, 390-406.
http://dx.doi.org/10.1016/j.physa.2006.05.018 - 10. Dunkel, J. and Hilbert, S. (2013) Inconsistent Thermostatistics and Negative Absolute Temperatures. arXiv:1304.2066v1 [cond-mat.stat.mech].
- 11. Dunkel, J. and Hilbert, S. (2014) Nature Physics, 10, 67-72; and Supplementary Information.
http://dx.doi.org/10.1038/nphys2815 - 12. Frenkel, D. and Warren, P.B. (2015) American Journal of Physics, 83, 163.
http://dx.doi.org/10.1119/1.4895828 - 13. Swendsen, R.H. and Wang, J.-S. (2014) Negative Temperatures and the Definition of Entropy. arXiv: 1410.4619v1 [cond-mat.stat.mech]
- 14. Hilbert, S., Hänggi, P. and Dunkel, J. (2014) Thermodynamics Law in Isolates Systems.
arXiv:1408.5382v1 [cond-mat.stat.mech] - 15. Niven, R.K. (2005) Physics Letters A, 342, 286-293. http://dx.doi.org/10.1016/j.physleta.2005.05.063
- 16. Niven, R.K. (2006) Physica A, 365, 142-149. http://dx.doi.org/10.1016/j.physa.2006.01.021
- 17. Elmaghraby, E.K. (2011) Journal of Modern Physics, 2, 1242-1246.
http://dx.doi.org/10.4236/jmp.2011.211154 - 18. Miranda, E.N. and Bertoldi, D.S. (2013) European Journal of Physics, 34, 1075.
http://dx.doi.org/10.1088/0143-0807/34/4/1075

