Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57151,11 pages
10.4236/jmp.2015.67092
Quantum Meteorites: An Extemporaneous Description of the System of the World
Jean-Paul Auffray
ex: Courant Institute of Mathematical Sciences, New York University, New York, NY, USA
Email: jpauffray@yahoo.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2015; accepted 12 June 2015; published 15 June 2015
ABSTRACT
We extemporaneously summarize the theoretical scheme we have introduced recently in this note to account for the (hidden) functioning of the System of the World at the quantum level. We further explore the relevance, the pertinence and the potential validity of this scheme. We obtain new fundamental results, bearing notably on the nature and the origin of the “virtual particles” conventionally called upon in quantum field theories to explain the Casimir Effect. We define the concept of quantum meteorites in this context. We disable the Heisenberg Uncertainty Principle, judged to be a (mis) interpretation of otherwise legitimate observations, and we replace it with our new XQP Absolute Certainty Principle.
Keywords:
Xonic Quantum Physics, Casimir Effect, Virtual Photons, Uncertainty Principle, Planck Length, Quantum Meteorites

1. Introduction
Extemporaneous speaking is said to be “a limited-preparation speech event based on research and original analysis”, perhaps “previously planned but delivered with the help of few or no notes” [1] .
We endeavor in the present note to extemporaneously review results we obtain in a preceding note concerning the functioning of the System of the World at the quantum level [2] and we derive new results.
To refer to the System of the World, we retrieved the word Scheme, and more precisely the expression theoretical Scheme, from the Greek “σχήμα” (skhēma), shape, or more generally, plan―a less technical definition than the one that Alexander Grothendieck attributed to this word in 1960 in his treatise Eléments de géométrie algébrique [3] . To him, for example, the equations x = 0 and x2 = 0 define the same points but different schemes. There is nothing of the sort with us in the present note, which is entirely dedicated to simplicity.
We carry out our quest while taking an imaginary leisurely thoughtful walk in the gardens of the ancient Lyceum in Athens, once a grove of trees named in honor of Apollo Lykeus (“Apollo as a wolf”) where Aristotle used to expose his doctrine while walking as he taught―i.e. extemporaneously (Figure 1).
2. Creating the World
Just as drawing is the art of projecting Reality on a plane, theoretical physics is the art―the game?―of using words and symbols (and/or equations) to describe how the System of the World (Nature) might be functioning in the shadows of Reality―i.e. in the hidden depths of the famous quantum realm.
Consider the Topological Unit Line Segment (ULS), which is nothing more than a modest straight line segment drawn with a pen on a piece of paper or a blackboard (Figure 2) and which is equipped with two “endpoints” 0 and 1―this is important:
0―――1
Hard to believe, but this is our starting point. Speaking of points… The ULS is made up of points glued together so to speak, so as to form a continuum, a concept difficult to define in simple words―there are no “interspaces” between any two contiguous points belonging to the ULS.
Remove (figuratively) all the points the ULS contains, leaving untouched the endpoints 0 and 1. Call what is left behind―i.e. the endpoints 0 and 1 with nothing (no points) left between them―the Void. Fill up the Void with the ULS again―allowing for a likely Imperfect Fit (IF). This IF will become significant later but let us ignore it for now.
We now have Chaos in the Void, so to speak―with one hic as the French would say (a hitch, a snag).
Nature is said to abhor the Void. According to our view, it also dislikes―abhors―continuity (points glued together) in its midst, and here is the hic: generated as we just described, our Chaos (future Universe) is made up
Figure 1. Aristotle (center to the right in blue) teaching extemporaneously in Athens as depicted by RaffaelloSanzio (Raphael) in his fresco Scuola di Atene. http://www.newbanner.com/AboutPic/Soa3.jpg
Figure 2. How to draw Unit Line Segments. http://en.wikipedia.org/wiki/Line_segment#/media/File:Fotothek_df_tg_0003359_Geometrie_%5E_Konstruktion_%5E_Strecke_%5E_Messinstrument.jpg
of points once again “glued together”, thereby forming a continuum.
To engender out of this continuum an acceptable Chaos, an “active principle”, the noX [2] , intervenes randomly repetitiously so as to “liberate” the points the continuum contains from any obligation of being connected by notions of proximity or distance with each other. In performing this task―randomly and repetitiously (iteratively)―the noX generates two kinds or species of (disconnected) points: i-points, which form a substrate (a Dust, a Mist); and e-points, which progressively establish in the Chaos a (hidden) structure in the framework of which they maintain the positions they originally occupied relative to each other in the original continuum.
In the context of his E infinity theory, Alexandria theoretician M. S. El Naschie calls our i-points Substrate the Empty set and the e-points Structure the Zero set.
We now have a somewhat organized Chaos in the Void: it contains a substrate―a Mist, a Dust―and a structure in formation, a most engaging beginning. Our representation of the System of the World painted with words and symbols is shaping up.
3. The Cantor Miracle
The reason why the description we just presented constitutes the basis for a legitimate representation of the System of the World is fascinating in itself. We briefly recall the story here for the benefit of the inquisitive reader of the present note.
In 1874, Saint-Petersburg born German mathematician Georg Cantor, then twenty-nine years old, published a paper entitled (our translation) “On a Characteristic Property of All Real Algebraic Numbers” [4] thereby found- ing the new branch of mathematics known since as Set theory. Three years later, in a letter he addressed to his mathematician friend Richard Dedekind, a former pupil of Gauss in Göttingen, Georg Cantor proved that for any positive integer n, there exists a 1-to-1 correspondence between the points on the ULS and all of the points in an n-dimensional space. Stunned by this discovery, Cantor exclaimed to Dedekind: “Je le vois, mais je ne le crois pas!” (“I see it, but I don’t believe it!”) [5] . This means that our ULS may be used to represent any n-di- mensional point sets (with n integer), for example the space-times currently favored by theoretical physicists. But we are going to have a problem when applying the theorem in the context of our scheme, because our e- points structure―El Naschie’s Zero set―has a dimension less than 1―it is not an integer n [2] .
4. What Is a Point? What Is a Principle?
The concept of pointis central in our considerations. It played a more than special role in Newton’s treatise, the famous Philosophiæ Naturalis Principia Mathematica. There is in fact much more to say concerning that question than what we were able to report in [2] .
The first two words in the treatise’s title translate unambiguously in English to “Of Natural Philosophy”― understand of Philosophy as it concerns Nature, but the last two words, “Principia Mathematica”?
Principia is commonly translated as Principles in English―Principes in French, Grundsätze in German, 原则 in Chinese, принцип in Russian… Very well, but when it is used in conjunction with the qualifier Mathematica the word acquires an altogether different meaning. As we showed in [2] , Mathematica for Newton meant alchemical, i.e. “active”, and Principia something like “ingredients”, e.g. when making bread, yeast is the active ingredient (it causes the wet flour to rise).
The noX is an active ingredient―an active principle―capable of acting on points in our scheme.
5. Little Bangs (Action) in the i-Points Substrate
As the noX discontinuously and iteratively disrupts the continuum organization which prevails in the Chaos, its counterpart, the Xon, also an active principle (duality), intervenes in the i-points substrate left behind by the noX, generating in its midst fleeting structures which appear as space lengths l and time lapse durationsd, controlled by two very simple relations:
lp = h, Ed = h
where p measures a momentum, E an energy, and where the symbol h, commonly known as the “Planck constant”, represents the action content of the elementary quantum of dynamical action.
6. Chaos in the Chaos
Sooner or later, contemporary physicists will have to come to terms with this reality: when he allowed―when he incited―physicists at large to think of his symbol h as representing a constant―Konstant for him, writing in German―the illustrious Founding Father of Quantum Physics, Max Planck, induced his followers to commit a deep error, the effects of which persist with us still today. In brief, he introduced Chaos in the Chaos.
It happened this way.
7. When Max Planck Went Wild
On May 18th 1899, then in his forty’s and a great believer in the fundamental merits of the thermodynamic concepts of Entropy and Energy, Max Planck presented a report to the Berlin Academy self-proclaiming enthusiastically his recently formulated logarithmic law of entropy to be a “Universal law of nature”. Following in the footsteps of several illustrious predecessors―James Maxwell and Karl Friedrich Gauss notably―he announced that he had undertaken the strenuous task of constructing a “Natural system of units” assigning units to all the physical entities known in his days. How? This is where he went wild: as functions of four “universal constants” (constants of Nature―Naturkonstante)―of his choosing, which he designated as a, b, c and f.
In embarking on this ambitious project, Planck had a grandiose plan in mind: “[These units], he asserted (our translation, our emphasis), will necessarily maintain their significance for all times and all civilizations, including extra-terrestrial and non-humans and hence can properly be called “Natural units” [Nature units]” [4] .
The four “universal constants” Planck selected to serve as building blocks of his Natural system of units are known today under modernized symbols (suggested by Planck himself, on second thoughts): a has become k and is known as the Boltzmann constant (even though Boltzmann had nothing to do with its invention); b has become h and is known as the Planck constant (see below); c remained c and is known as measuring the speed of light in vacuum; f has become G and is known as the Newton gravitational constant (even though Newton never used it in his calculations).
The use of the qualifier “constant” [Konstant] by Planck in his ambitious undertaking and the abusive use of the word quantum―which signifies nothing more than “quantity” (amount)―are at the roots of the uncontrolled erratic way QP has developed.
Planck’s h has the dimension of angular momentum. In calling it a “constant”, Planck presumably meant to say (to suggest) that, in all likelihood, it would preserve its significance, its value as a “quantity”―its value as “the quantum”―for all times and all civilizations. At the same time, he was well aware of the true significance of his invention. In a paper he published in 1907 after he had discovered that his h is a “Poincaré relativistic invariant”, raising the possibility, wrote Planck, that “each and every change in nature corresponds to a definite number of action elements completely independent of the choice of coordinate system.”
Each and every change in Nature… A remarkable statement indeed, which is in full agreement with the basic concepts of our Xonic Quantum Physics project (XQP) and with the results we have obtained so far [2] .
But physicists understood and continue to understand the meaning of Planck’s word “Konstant” differently. The “Planck constant” has appeared ever since in thousands and thousands of equations published around the world in every kind of position within the equations, precisely as one would be allowed to do mathematically if, instead of h, the constant involved was the Archimedes’ constant π, for example.―or Euler’s number e, or Pythagoras’ constant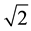 , or Descartes’ imaginary unit i, or the golden ratio φ, or, if one wants to be a bit fancy, the Champernowne constant C10 = 0.12345678910111213141516・・・ which, like the golden ratio, is an irrational number dotted of extraordinary properties; for example its value is reproduced by the banal ratio 10/81 with an error of the order of 1 × 10−9 only; and if you expand it as a continued fraction keeping the first 18 terms, the error is reduced to approximately 1 × 10−190. And to concludethis non-exhaustive list of legitimate “constants” with a touch of humor (we are doing theoretical physics, which is a game, isn’t?), why not include in our list of “true” constants the number Zero, which came into the English language via the French zéro from the Arabic Sifr (صفر) meaning “empty”, translation of the Sanskrit śūnya (शून्य).
, or Descartes’ imaginary unit i, or the golden ratio φ, or, if one wants to be a bit fancy, the Champernowne constant C10 = 0.12345678910111213141516・・・ which, like the golden ratio, is an irrational number dotted of extraordinary properties; for example its value is reproduced by the banal ratio 10/81 with an error of the order of 1 × 10−9 only; and if you expand it as a continued fraction keeping the first 18 terms, the error is reduced to approximately 1 × 10−190. And to concludethis non-exhaustive list of legitimate “constants” with a touch of humor (we are doing theoretical physics, which is a game, isn’t?), why not include in our list of “true” constants the number Zero, which came into the English language via the French zéro from the Arabic Sifr (صفر) meaning “empty”, translation of the Sanskrit śūnya (शून्य).
One of the early victims of the misconstrued play on words concerning the “Planck constants” and his “constant h” in particular, was a certain Albert Einstein, then working as a modest Technical Expert Third Class at the Swiss Patent Office in Bern.
Einstein published his second academic paper in 1905. It covers seventeen pages and proposes some fifty-two equations. In presenting them, Einstein uses some standard notation―E for energy, S for entropy―but he also uses some symbols of his own―L for the speed of light (?) and β to represent the “ratio” h/k of the “Planck constant” h and the “Boltzmann constant” k. And here is the decisive, the telling detail: even though these two “constants” have different dimensions, Einstein assigned to their ratio the numerical value
β = 4866 × 10−31.
placing surreptitiously a period after the equation without providing any indication of dimensions―as if β was a pure number [6] .
As a result of the generalization of such malpractices, the Edifice of contemporary Quantum Physics (EQP) has become a Leaning Tower perilously tilted to one side (Figure 3).
In our scheme, h can appear in an equation only if the equation is written in the form
“something” = h
with “something” having the dimension of dynamical action, and more precisely of angular momentum―spin.
The relations lp = h and Ed = h which prevail in our scheme differentiate this scheme from all other quantum theoretical models of Reality, which allow the Planck “constant” h to enter their equations in any odd way, assuredly one of the most extravagant (mis) uses of a concept in the history of theoretical physics. (The misuse of the word “Energy” is also flagrant).
Speaking of Energy… let us note, passim, that―at least at this stage of our investigations―the two relations lp = h and Ed = h are independent of each other. Each generates Little Bangs on its own.
Let us leave this question aside for now and turn our attention to something else.
What is missing in our Chaos at this stage for it to become the Cosmos―the Universe?
Figure 3. The Huqiu Tower which has been named China’s Leaning Tower of Pisa. http://www.china.org.cn/images/38257.jpg
Particles (i.e. matter).
Maybe particles are there, hidden in our scheme and we have not noticed them yet…
That would help.
Before we look for particles in our System of the World, let us investigate the possibility that our scheme contains something significant, but simpler than particles, that we have failed to recognize hitherto.
8. Prospects
A bright new idea sometimes emerges as the result of a chance encounter. While pondering these questions, we recalled an intriguing proposal made some time ago by Californian theoretician Steve Olah under the appellation The Kinetic Universe. We retrieved S. Olah’s paper [7] .
Presenting his theory, Steve Olah writes: “For the Kinetic Universe we revive and redefine Aether”, asserting: “Aether provides the infrastructure for our existence.”
Aether… another word of Greek origin…
Olah’s Kinetic model relies on kinetic energy and avoids “the use of ghostly fields and massless mediators” a fact which makes it very attractive from the viewpoint of our scheme. Indeed, the fundamental motors which run the System of the World in our scheme are fueled by dynamical action, not by kinetic energy, but let not this prevent us from exploring the road S. Olah opened.
9. Generating Momentum in the Chaotic Substrate
The relation lp = h describes how the xon generates in the System of the World space lengths l associated with (linear) momenta p, and/or conversely (Figure 4).
This raises two related fundamental questions that we shall now address.
The first is: in the relation lp = h does the length l refer to a physical space length composed of i-points “glued together” again so as to form true (geometric) line segments―i.e. localized, fleeting (mini) continuums?
Or does it represent―measure―the length of the path that a single i-point―an aethon!―follows in the Chaos while driven by the momentum p?
We used the word “path” deliberately here, in memory of the great Richard Feynman who used this word in his QED theory to designate trajectories in action, not in space or time―precisely as we do in our scheme.
In a subtle way, the two interpretations might be equivalent, just as the strike of light a meteor traces in the sky as it crosses the atmosphere is both, the meteorite and its path.
The second related question is: momentum is normally carried by entities―by particles―which possess a mass. As far as his Kinetic Universe is concerned, S. Olah says it clearly: “In the Kinetic Universe force and
Figure 4. Generating momentum. http://sr.photos3.fotosearch.com/bthumb/CSP/CSP992/k14094769.jpg
pressure is [sic] created with collisions of elementary particles that have mass”, assuring: “Collisions can’t pull, collisions can only push.”
Where are the masses in our scheme?
The standard relativistic momentum expression for a particle with rest mass m0 moving at velocity v is

with c the speed of light. As v approaches c, this expression approaches 0/0 and cannot be used. One uses instead the alternate relativistic energy relation
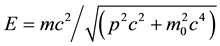
which yields, for m0 = 0

This is our fundamental relation!
Thus, by the standard use of well-established relativistic relations, we find that our i-points do not require being equipped with a rest mass to be able to carry momentum. This is in fact precisely the reasoning physicists use to explain and justify the fact that photons, which possess no rest mass, carry a momentum nevertheless.
From these considerations, new aspects of our undertaking emerge that we shall now examine.
10. Wirkung
At the end of his life, Max Planck expressed a regret: “All matter originates and exists only by virtue of a force which brings the particles of an atom to vibration and holds this most minute solar system of the atom together [8] .” He had not fully realized, even then, that he had identified the said “force” at the very beginning of his academic career―and that he had given it almost the right name, calling it Das Elementares Wirkungsquantum, even though instead of the word Wirkung―which translates to “Effect” in English―he would have been better inspired to use the word Aktion―Action in English―since he was referring very precisely to the concept forged in 1689-1692 by Wilhelm Gottfried Leibniz under the Latin name Actio―“Dynamical action” for us today in this note.
Speaking of Wirkung… Let us examine the possibility that some “Effect” already discovered might hold the key to a better understanding of the workings of our scheme.
We did not have to look very far. Dr M. S. El Naschie called our attention to an Effect he felt was apt to do the trick [9] .
11. An Effect without a Cause
The ancient Greeks used the word phenomenon (φαινόμενoν, phainomenon, from the verb φαίνειν, phainein, “to show, shine, appear, to be manifest (or manifest itself)”) to refer to events occurring in the celestial spheres (solar eclipses for instance). They used the word meteor (μετέωρον, metéōron, “lofty”) to designate events occurring in the terrestrial spheres―wind, rain, snow, meteorites… Our contemporary use of the word (and the concept) Meteorology reflects this ancient subtle difference
In 1948, a stunning “meteor”―now called an “Effect”―was conceived by two Dutch theoretical physicists, Hendrik Brugt Gerhard Casimir and Dirk Polder, then working at the Philips Natuurkundig Laboratorium (Philips Physics Laboratory, NatLab) in Eindhoven in the Netherlands. It is known to us today after the name of one of the two dreamers as the Casimir Effect. The “force” said to be involved in the Effect is the Casimir-Polder Force. The basic functioning of the Casimir Effect is easily described. Place two polished plates (two mirrors) facing each other a short distance apart in a container equipped with a vacuum pomp. Empty the container of all the air it contains as best you can so as to realize a vacuum in the container and watch what happens then. The plates start moving toward each other as if mutually attracted to each other by the simple presence of the vacuum.
12. What Takes Place in the Vacuum? Official Explanation(s)
Quantum field theoreticians tell us that fundamental “fields”―notably the “electromagnetic field”―present in the vacuum are “quantized” at each and every point in space, causing these fields to act locally as “virtual particles”. Then, they say, if there are fewer of these virtual particles in the space between the plates than outside that space, the “pressure” the virtual particles generate against the plates will be less on one side of the plates and the plates will be “pushed” toward each other―as if “attracting” each other.
In their original prediction of the Casimir effect, Hendrik Casimir and Dirk Polder reasoned in terms of “energy”, not in term of “dynamical action” as we do in our scheme. They (more or less implicitly) assumed:
1) That the virtual particles in their proposed experiments are “virtual photons”―after all photons are supposed to be the carriers of energy in this conception of Quantum Physics; and
2) That only those virtual photons whose wavelengths fit a whole number of times into the gap between the plates should be counted when calculating the “vacuum energy”.
Hendrik Casimir and Dirk Polder did not know it then, but they were playing in our courtyard! For what better incarnation of “virtual particles” than our moving i-points? Particularly when, to “explain” their Effect, our learned Dutch physicists also spoke of “vacuum fluctuations”―a well-chosen designation indeed, to describe the deconstruction-construction processes which occur discontinuously in our i-points substrate―in El Naschie’s Empty set which in our scheme represents the vacuum.
13. An i-Point in Motion Is a Quantum Meteorite!
In the framework of our scheme, what takes place between the plates follows a simple scenario. The Little Bangs which discontinuously deconstruct and (re)construct space lengths l in the i-points substrate generate “real” virtual particles in the form of i-points which follow paths of lengths l, the specific value being determined randomly. Lengths greater than the distance L separating the plates cannot properly fit in the space between the plates, too narrow for them. As a consequence, the Little Bangs accumulate randomly fewer moving i-points in the space between the plates than outside that space; a (random) selection occurs which generates what M. S. El Naschie calls a “topological pressure gradient” which drives the plates toward each other―once again in accordance with the Olah diktat: “Collisions can’t pull, collisions can only push”. In the end we are led to make this stunning observation: a ni-point in motion is a quantum meteorite! (Figure 5, Figure 6). As for the mathematics… insofar as they are relevant, they apply unchanged in the frame of our scheme since it is only the nature and the origin of the “virtual particles” involved that we have redefined.
14. What’s Next?
The result we just obtained is so delightful that it invites us to conclude this note without further ado. We’ll do so… immediately after we indulge in one last fun endeavor.
In [10] , we inaugurated the Physics Museum of Obsolete Concepts, the PMOC, and we placed General
Figure 5. The Casimir effect. http://www.scientificamerican.com/article/what-is-the-casimir-effec/
Figure 6. Meteorites striking their paths into the night. https://sp.yimg.com/ib/th?id=JN.sffs2avmEvpD2vZo2imb8A&pid=15.1&w=184&h=114&p=0
Relativity space-times in good stand in its midst. We shall open here today a new gallery in the PMOC, the Gallery of Specious Good Ideas (GSGI) and we shall move in it one of the pillars of the QP Leaning Tower Edifice… the Heisenberg Uncertainty Principle. Here is why.
Born in 1901, young Werner Heisenberg conceived his Uncertainty Principle in 1927 on the basis of a deep personal philosophical conviction. He asserted (our translation): “Even in principle, we cannot know the present in all detail”, leading him to make this remark which concerns Quantum Physics directly: “The more precisely the position [of an electron] is determined, the less precisely the momentum is known in this instant, and vice versa.” [11] .
To sustain his argument, Heisenberg imagined a thought experiment in which a gamma-ray microscope is used to observe an electron and determine its position, He wrote (our translation, his notation): “Let q1 measure the precision with which the value q is known (q1 is something like the average error on q), in our case the wavelength of the gamma ray, p the precision with which the value p can be determined, here the discontinuous change in p1 produced by the Compton effect, then by the elementary Compton effect formulae p1 and q1 satisfy the following relation p1q1 ~ h.”
When a Magician wants to execute atour de passe-passe―a conjuring trick in English, Zauberei in German, 魔术伎俩in Chinese, truco de magia in Spanish, Заклинаятрюк in Russian… he calls your attention to something else at the instant he performs the trick. The surreptitious hypothesis Heisenberg made in developing his attack against the Principle of causality is “hidden” within parentheses in the declaration quoted above. When he writes “(q1 is something like the average error on q)”, he expresses not a fact, but a predetermined desire to find uncertainties in QP measurements.
We don’t need to go further. In a slightly different notation, Heisenberg’s relation p1q1 ~ h is our fundamental relation lp = h. The only difference is in the interpretation given.
As per our scheme, the Heisenberg Uncertainty Principle is a specious interpretation of the basic relation lp = h and as such deserves to be placed in in our PMOC-SGI gallery and we shall replace it with…
The Xonic Absolute Certainty Principle (ACP)
An i-point moving with momentum p follows a Feynman-like path of length l such that the composition of l with p satisfies the relation lp = h with an Absolute Certainty (Figure 7).
By the way…Where in the world―where on Earth―should we install our SGI gallery? At the core of an intricate Labyrinth built on the model of the elaborate structure the legendary Daedalus once constructed at Knossos for King Minos of Crete to serve as a prison from which the Minotaur would be unable to escape…?A better idea came to mind. To say it differently, why not place our precious SGI under the protection of the mischievous creature-god “Man in the Maze”, the litoi, said to reside in a cave below the peak of the Baboquivari Mountain in the Tohono O’odham Nation in Arizona (Figure 8).
And let us not forget, even though we have not stressed it during the course of this leisurely visit in the inner hidings of the System of the World, that everything in it is spinning―at the quantum level our two active principles,
Figure 7. Following a path with absolute certainty. https://sp.yimg.com/ib/th?id=JN.j2N2hTuJy2hyfpxkR1oBfA&pid=15.1&P=0
Figure 8. The Baboquivari Peak, home of the Litoi. A good place to hide in security “for all times and all civilizations” the Heisenberg Uncertainty Principle. http://www.sangres.com/arizona/blm/baboquivaripeak.htm#.VRwuGvmsXxU
the noX and the Xon, in a way are pure spin and convey this intrinsic characteristic to everything they touch― our quantum meteorites carry spin as they travel!
It is noteworthy that in the universe at large, everything seems to be rotating, as pointed out to us by Canadian philosophically-minded Xiang He (private communication). Spin and (classical) rotation might arise from the same cause―for us the noX and the Xon―at this stage a pure speculation (Figure 9).
15. Conclusions
Following a suggestion made by M. S. El Naschie, we examine in this note how the Casimir Effect can be―is to be―understood in the framework of the theoretical scheme we have developed step by step in recent publications under the generic name Xonic Quantum Physics (XQP) in conjunction with M. S. El Naschie’s E infinity theory. This analysis has led us to the unexpected discovery of a pleasant double new treasure: moving i-points which occur in our scheme may properly be said to be real virtual particles and to constitute quantum meteorites, i.e. spinning point-like “objects” moving along Feynman-type paths in the sky of the Quantum World.
A subjacent System of the World animated by spurious Little Bangs and flashy rotating Quantum Meteorites… who can want anything more? We shall conclude this paper on these high notes and reserve the consideration of other perturbing related topics for forthcoming publications, e.g. the relation Ed = h (Figure 10).
Figure 9. When everything in the universe is rotating. https://sp.yimg.com/ib/th?id=JN.dIMIWggIN44j0Bv%2fLaPZcQ&pid=15.1&P=0
Figure 10. Spurious little bangs and flashy quantum meteors… https://sp.yimg.com/ib/th?id=JN.%2bsBy8WFsmYKQ0Nv7KUDN7A&pid=15.1&P=0
Acknowledgements
We gratefully acknowledge Professor M. S. El Naschie’s contribution to the work reported in this note when he suggested to us the Casimir Effect as a possible source of inspiration related to our study. We also wish to express our gratitude to Ms. Clara Gao and to Ms. Kelly Sang, JMP Editorial Board Assistants, for their valuable help and advice in properly formatting this note for publication.
References
- http://en.wikipedia.org/wiki/Extemporaneous_speaking
- Auffray, J.-P. (2015) Journal of Modern Physics, 6, 536-545. http://dx.doi.org/10.4236/jmp.2015.65058
- http://webusers.imj-prg.fr/~leila.schneps/grothendieckcircle/unpubtexts.php
- Planck, M. (1899) Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 5, 440-480.
- See for Instance http://www-history.mcs.st-andrews.ac.uk/Quotations/Cantor.html
- Einstein, A. (1905) Annalen der Physik, 17, 132-148. http://dx.doi.org/10.1002/andp.19053220607
- Olah, S. (2014) The Kinetic Universe. A View From Outside of the Box. http://gsjournal.net/Science-Journals/Research%20Papers-Unification%20Theories/Download/5528
- Planck. M. Max Planck Quote. http://izquotes.com/quote/146303
- El Naschie, M.S. (Private Communication). See also, El Naschie, M.S. (2015) World Journal of Nano Science and Engineering, 5, 26-33.
- Auffray, J.-P. (2014) Journal of Modern Physics, 6, 5. http://dx.doi.org/10.4236/jmp.2014.515144
- Heisenberg, W. (1927) Zeitschrift fürPhysik, 43, 172-198. English Translation in (Wheeler and Zurek, 1983), 62-84.











