Journal of Modern Physics Vol.06 No.02(2015), Article ID:54153,9
pages
10.4236/jmp.2015.62015
Pion, Kaon and Antiproton Production in
 Collisions at LHC Energy
Collisions at LHC Energy
 TeV: A Model-Based Analysis
TeV: A Model-Based Analysis
Pradeepta Guptaroy1*, Sima Guptaroy2
1Department of Physics, Raghunathpur College, Raghunathpur, India
2Department of Physics, Basantidevi College, Kolkata, India
Email: *gpradeepta@gmail.com, simaguptaroy@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 26 January 2015; accepted 13 February 2015; published 16 February 2015

ABSTRACT
Large Hadron Collider (LHC) had produced a vast amount of high precision data for
high energy heavy ion collision. We attempt here to study i) transverse momenta
spectra, ii)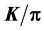 ,
,
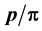 ratio behaviours, iii) rapidity
distribution, and iv) the nuclear modification factors of the pion, kaon and antiproton
produced in
ratio behaviours, iii) rapidity
distribution, and iv) the nuclear modification factors of the pion, kaon and antiproton
produced in
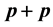 and
and
 collisions at energy
collisions at energy
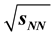 = 2.76 TeV, on the basis of Sequential Chain Model (SCM). Comparisons of the model-based
results with the measured data on these observables are generally found to be modestly
satisfactory.
= 2.76 TeV, on the basis of Sequential Chain Model (SCM). Comparisons of the model-based
results with the measured data on these observables are generally found to be modestly
satisfactory.
Keywords:
Relativistic Heavy Ion Collisions, Baryon Production, Light Mesons

1. Introduction
Heavy ion collisions at ultra relativistic energies might produce a new form of
QCD matter characterized by the deconfined state of quarks and gluons (partons)
[1] . Measurements of the production of identified particles provide information
about the dynamics of this dense matter. The yield of identified hadrons, their
multiplicity distributions, as well as the rapidity and transverse momentum spectra
are the basic observables in proton-proton and heavy ion collisions at any energy
regime, from a few GeV per nucleon to the new ultra-relativistic LHC regime, spanning
c.m. energies of a few TeV [2] . Recently, the different experimental groups in
the CERN Large Hadron Collider (LHC) have reported various results for different
observables in
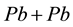 collisions at energy
collisions at energy
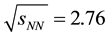 TeV. These results might provide another opportunity to investigate the bulk properties
of exotic QCD matter, the so-called QGP-hypothesis. But the exact nature of QGP-hadron
phase transition is still plagued by uncertainties [3] .
TeV. These results might provide another opportunity to investigate the bulk properties
of exotic QCD matter, the so-called QGP-hypothesis. But the exact nature of QGP-hadron
phase transition is still plagued by uncertainties [3] .
Our objective in this work is to use a model, known as “Sequential Chain Model (SCM)”,
which is different from “standard” framework, in interpreting the transverse momenta
spectra, some ratio-behaviours, rapidity spectra and the nuclear modification factor
of the pions, kaons and antiprotons produced in
 and
and
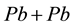 collisions at LHC energy
collisions at LHC energy
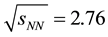 TeV. Very recently, some questions have been arose about the quark constituents
of the nucleons. Little of the proton spin is carried by the quarks [4] . So, in
order to explain the huge amount of heavy ion collision data, we put forward this
model which has no QGP-tag and is different from the quark-hypothesis.
TeV. Very recently, some questions have been arose about the quark constituents
of the nucleons. Little of the proton spin is carried by the quarks [4] . So, in
order to explain the huge amount of heavy ion collision data, we put forward this
model which has no QGP-tag and is different from the quark-hypothesis.
The organization of this work is as follows. In Section 2, we give a brief outline of our approach, the SCM. In the next section (Section 3), the results have been presented with table and figures. And in the last section (Section 4), we offer the final remarks and conclusions.
2. Outline of the Model
This section is divided by two subsections 1) the basic model in
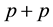 collision and 2) subsequent trans- formation to the
collision and 2) subsequent trans- formation to the
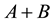 collisions.
collisions.
2.1. The Basic Model: An Outline
According to this Sequential Chain Model (SCM), high energy hadronic interactions
boil down, essentially, to the pion-pion interactions; as the protons are conceived
in this model as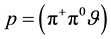 ,
where
,
where
 is a spectator particle needed for the dynamical generation of quantum numbers of
the nucleons [5] - [11] .
is a spectator particle needed for the dynamical generation of quantum numbers of
the nucleons [5] - [11] .
The inclusive cross-section of the



with

where











where


Similarly, for kaons of any specific variety (




with

And for the antiproton production in


with

2.2. The Path from pp to AB Collisions
In order to transform the inclusive cross-section from







Here, in the above equation [Equation (8)], the first factor gives a measure of
the number of wounded nucle- ons i.e. of the probable number of participants, wherein









with


The second term in expression (8) is a physical factor related with energy degradation
of the secondaries due to multiple collision effects. The parameter



3. The Results
This section will be divided in the following sub-sections: i) the










3.1. Transverse Momenta Spectra of Charged Hadron in



We can write from expression (8), the transformed SCM-based transverse-momentum
distributions for


where, for example, the parameter


In a similar way, the values of








3.1.1. Production of




In Table 1, the calculated values of






In Figure 1, we have drawn the invariant yields
against




3.1.2. Invariant Yields of




In a similar fashion, the invariant yields of







3.2. The K/π and p/π Ratios
The model-based




3.3. The Rapidity Distribution
For the calculation of rapidity distribution, we can make use of the following standard relation [17] ,

Table 1. Values of




Figure 1. Plots for





Figure 2. Centrality dependence
of the






Table 2. Values of







Figure 3. Ratios of (a)





By using Equation (1), Equation (8), Table 2 and Equation (12), we arrive at the SCM-based rapidity dis- tribution, which is given hereunder;

The



In Figure 4, we have plotted theoretical


3.4. The Nuclear Modification Factor
The nuclear modification factor (NMF)





where



Here,


The



In the region,


The SCM-based results on NMF’s for









Figure 4. Plot of rapidity
distribution of



Figure 5. Plots for






4. Discussions and Conclusions
Let us now make some comments on the results arrived at and shown by the diagrams on the case-to-case basis.
1) The invariant yields against transverse momenta






2) Similarly, in calculating the yields for different transverse momenta and for
different centralities for





3) The





4) In explaining the rapidity distribution for production of pions (Figure 4), the majority of the produced secondaries, the model works agreeably with data. The comparison with Gaussian fit is satisfactory.
5) The nuclear modification factors for pion, kaon and proton for central



Now, let us sum up our observations in the following points: 1) The model under
consideration here explains the data modesly well on


Acknowledgements
The work is supported by University Grants Commission, India, against the order no. PSW-30/12(ERO) dt.05 Feb-13.
References
- Abelev, B. [ALICE Collaboration] (2014) Physics Letters B, 736, 196-207. http://dx.doi.org/10.1016/j.physletb.2014.07.011
- Riggi, F. (2013) Journal of Physics: Conference Series, 424, Article ID: 012004. http://dx.doi.org/10.1088/1742-6596/424/1/012004
- Zhang, S., Han, L.X., Ma, Y.G., Chen, J.H. and Zhong, C. (2014) Physical Review C, 89, Article ID: 034918. http://dx.doi.org/10.1103/PhysRevC.89.034918
- de Florian, D., Sassot, R., Stratmann, M. and Vogelsang, W. (2014) Physical Review Letters, 113, Article ID: 012001. http://dx.doi.org/10.1103/PhysRevLett.113.012001
- Guptaroy, P. and Guptaroy, S. (2014) Chinese Physics Letters, 31, Article ID: 082501. http://dx.doi.org/10.1088/0256-307X/31/8/082501
- Guptaroy, P., Goutam, S. and Bhattacharyya, S. (2012) Journal of Modern Physics, 3, 116-123. http://dx.doi.org/10.4236/jmp.2012.31016
- Guptaroy, P., Sau, G., Biswas, S.K. and Bhattacharyya, S. (2010) IL Nuovo Cimento B, 125, 1071-1097. http://dx.doi.org/10.1393/ncb/i2010-10913-4
- Guptaroy, P., De Bhaskar, Sau, G., Biswas, S.K. and Bhattacharyya, S. (2007) International Journal of Modern Physics A, 28, 5121-5154. http://dx.doi.org/10.1142/S0217751X07037251
- Bandyopadhyay, P. and Bhattacharyya, S. (1978) IL Nuovo Cimento A, 43, 305-322. http://dx.doi.org/10.1007/BF02730432
- Bhattacharyya, S. (1988) IL Nuovo Cimento C, 11, 51-65. http://dx.doi.org/10.1007/BF02507895
- Bhattacharyya, S. (1988) Journal of Physics G: Nuclear Physics, 14, 9-17. http://dx.doi.org/10.1088/0305-4616/14/1/005
- Guptaroy, P., Sau, G., Biswas, S.K. and Bhattacharyya, S. (2008) Modern Physics Letters A, 23, 1031-1046. http://dx.doi.org/10.1142/S021773230802567X
- Wong, C.Y. (1994) Introduction to High-Energy Heavy Ion Collisions. World Scientific, Singapore. http://dx.doi.org/10.1142/9789814277549
- Abreu, M.C., Alessandro, B., Alexa, C., Arnaldi, R., Atayan, M., Baglin, C., et al. (2002) Physics Letters B, 530, 33-42. http://dx.doi.org/10.1016/S0370-2693(02)01352-7
- Chatrchyan, S., Khachatryan, V., Sirunyan, A.M., Tumasyan, A., Adam, W., Aguilo, E., et al., the CMS Collaboration (2012) The European Physical Journal C, 72, 2164. http://dx.doi.org/10.1140/epjc/s10052-012-2164-1
- Abelev, B., Adam, J., Adamová, D., Adare, A.M., Aggarwal, M.M., Aglieri Rinella, G., et al. (2013) Physical Review C, 88, Article ID: 044910. http://dx.doi.org/10.1103/PhysRevC.88.044910
- Kaidalov, A.B. and Ter-Martirosyan, K.A. (1984) Soviet Journal of Nuclear Physics, 39, 979.
- ALICE Collaboration (2013) Physics Letters B, 726, 610-622. http://dx.doi.org/10.1016/j.physletb.2013.09.022
- Otwinowski, J. (2013) High-pT Processes Measured with ALICE at the LHC. arXiv:1301.5285v1 [hep-ex]
- Chojnacki, M., for the ALICE Collaboration (2014) Journal of Physics: Conference Series, 509, Article ID: 012041. http://dx.doi.org/10.1088/1742-6596/509/1/012041
NOTES
*Corresponding author.








