Received 23 September 2014; revised 21 October 2014; accepted 15 November 2014

ABSTRACT

We present a theoretical study on the terahertz (THz) optoelectronic properties of long-period InAs/GaSb type-II super lattices (SLs). The eight-band k・p model is used to calculate the electronic structures of such SLs and on the basis of band structures, the Boltzmann equation approach is employed to calculate the optical absorption coefficients for the corresponding SL systems. It is found that long-period InAs/GaSb type-II SLs have a considerable absorption in the THz bandwidth. By examining the dependence of THz absorption coefficient on the InAs/GaSb layer widths, we demonstrate that with a proper choice of InAs/GaSb layer widths, an optimized THz absorption can be achieved. This study is pertinent to the potential application of InAs/GaSb type-II SLs as THz photo detectors.

Keywords:

Long-Period InAs/GaSb Type-II SLs, THz Optoelectronic Properties, THz Band-Gap and Absorption

1. Introduction

Superlattice (SL) is a periodic structure that consists of alternating thin layers of different materials. These thin material layers are typically measured in nanometers. SLs have unique electronic, optical and optoelectronic properties and have important applications in advanced electronic and optoelectronic devices. It is known that any design of efficient photon detectors should address such two basic problems as 1) an appropriate band-gap and 2) a marked effect of optical absorption induced by the presence of such a band-gap. At present, short-pe- riod InAs/GaSb type-II SLs have been successfully applied as uncooled mid-infrared (MIR) photodetectors. Their electronic and optical properties in the MIR bandwidth have been intensively investigated both experimentally and theoretically [1] -[12] . It has been found experimentally that for short-period InAs/GaSb type-IISLs with the layer widths around 21/24 angstrom, a strong photo-response signal can be observed in the MIR bandwidth and the cut-off wavelength can be tuned effectively by varying the InAs/GaSb layer widths [4] . However, there are few works on the electronic and optical properties of such SLs in the terahertz (THz) bandwidth. In this paper, we propose that long-period InAs/GaSb type-II SLs could be potentially used for the THz photodetection. The main physical basis for the present proposal is that the appropriate THz band-gap can be achieved in InAs/GaSb type-II SLs by tuning the InAs and/or GaSb layer widths. Through further engineering the band structures of such SLs, their THz absorption properties induced by the interaction between electrons and THz light radiation can be optimized. We therefore expect that the strong THz photo-response can be realized from such SLs. Moreover, from the viewpoint of material growth and device fabrication, long-period SLs are easier to grow in comparison to those with short periodicities. As pointed out by previous work [5] , the growth of high- quality MIR photodetectors using short-period InAs/GaSb SLs is still quite challenging due to the complexity of growing alternating thin layers.

In our previous work [13] , we have theoretically investigated the electronic and optical properties of long-period InAs/GaSb type-II SLs in the THz bandwidth. In that work, we have used the Kronig-Penney model (a single- band effective-mass model) to calculate the SL miniband structure and associated wavefunctions [14] . Within this model, the electron and hole states were solved separately. However, such a single-band treatment is not fully accurate to describe the material systems with relatively narrow band-gaps such as InAs/GaSb type-II SLs. In particular, the important effect such as conduction-valence band coupling or mixing in such SL structures cannot be considered using the Kronig-Penney model. Therefore, a multi-band treatment by including the band coupling effect is needed for an in-depth and more accurate description of such material systems. In this work, we employ an eight-band model to calculate the electronic structures of long-period InAs/GaSb type-II SLs. On the basis of electronic structure results, the Boltzmann equation approach is then employed to calculate the optical absorption coefficient for the corresponding SL systems. The prime motivation of the present study is to find out the idea and strategy to optimize the THz absorption properties of long-period InAs/GaSb type-II SLs through examining the dependence of THz absorption coefficient on the sample parameters such as the InAs/ GaSb layers widths. We intend to understand more deeply and more rightly the physical mechanisms behind the potential application of long-period InAs/GaSb type-II SLs as THz photodetectors.

This paper is organized as follows. In Section 2, we briefly outline the theoretical approach for calculating the electronic and optical properties of InAs/GaSb type-II SLs. In Section 3, the numerical results are presented and discussed. Finally, the concluding remarks are provided in Section 4.

2. Theoretical Approach

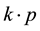We consider an InAs/GaSb SL with a type-II band alignment, as schematically shown in Figure 1. The growth direction is taken as the z-axis which is along the [001] direction, and the x-axis and y-axis are long the [100] and [010] directions, respectively. Assume the InAs/GaSb layer widths are, then the SL periodicity is given by. The eight-band model is a good start point for studying narrow-gap semiconductor systems [15] such as InAs/GaSb type-II SLs. The main parameters used in this model Hamiltonian include the fundamental band-gap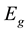, the Kane energy parameter, the spin-orbit splitting energy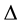, the conduction-band electron effective mass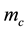, and the valence-band Luttinger parameters, 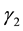and.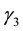

With the envelope function theory [16] , the energy dispersions and the corresponding wave functions for the SL are derived from the following Schrödinger equation

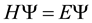, (1)

where 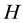is the usual eight-band 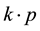Hamiltonian which has been well documented elsewhere [11] [12] [17] -[19] , 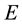is the carrier energy and 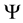the corresponding wave function. Due to the translation symmetry in the -plane of the SL, and in the Hamiltonian are good quantum numbers while should be replaced by the differential operator since the considered SL is grown along the z-axis. The above Schrödinger equation is numerically solved using the plane-wave expansion method [18] .

With the SL electronic structure obtained, we can calculate the optical properties of the InAs/GaSb type-II SL system such as the optical matrix element, the optical transition rate and the optical absorption coefficient.

Adopting the formalism developed in Ref. [20] , the optical matrix element between the initial state and the final state involved in the optical transition process can be written as

, (2)

where, is the wave vector introduced by the periodical boundary condition of the SL system, and are different miniband indices, is the free-electron effective mass, is the reduced Plank’s constant, and is the unit vector of light polarization direction. Inserting the optical matrix element into the Fermi’s golden rule, the electronic transition rate induced by direct carrier-photon scattering can be obtained as

, (3)

where is the electron charge, and and are the strength and frequency of radiation field, respectively.

In this work, we employ the energy-balance equation [21] derived from the Boltzmann equation as the governing equation to study the photo-response of carriers in a SL to the applied radiation field. Using the energy- balance equation approach, the optical absorption coefficient of a SL system can be obtained as [11]

, (4)

where, , and are, respectively, the dielectric constants of the material layer and the free space, is the velocity of light in vacuum, and is the Fermi-Dirac distribution function. The optical absorption coefficient in Equation (4) is calculated numerically. In the numerical calculation, the delta function in this equation is broadened by the normalized Gaussian distribution [22] .

3. Results and Discussion

In this work, we are interested in long-period InAs/GaSb type-II SLs which are proposed for the photo detection in the THz bandwidth. We first perform the electronic structure calculations for such SLs. With the electronic structures obtained, the optical coefficients such as the absorption coefficients for the corresponding SL systems are then evaluated. The parameters used in the electronic-structure calculation such as, , , , and are taken from Ref. [23] . The bottom of the conduction band in the In As layer is taken as the energy reference and is set to be zero. The valence band offsets are 0.56 eV for the GaSb/InAs hetero junction [23] . The dielectric constants of InAs and GaSb layers used in the optical-absorption calculations are 15.15 and 15.69, respectively. Furthermore, in the present study, we do not consider 1) the interface effect since the thickness of interface layer can be negligible compared with the whole SL periodicity and 2) the strain effect due to the small lattice mismatch between InAs and GaSb layers as pointed out by Ref. [23] .

We use a typical long-period InAs/GaSb type-II SL to display the main results of our electronic structure calculation. The InAs/GaSb layer widths are taken as. The calculated band structure is shown in Figure 2, where is the in-plane wave vector and is the wave vector along the growth direction. There are five energy bands shown in this figure, labeled as CB1 and CB2 for the ground-state and first-excited electron energy bands, and HH1 and HH2 for the ground-state and first-excited heavy-hole energy bands. The assignment of the carrier type to various energy bands follows from the associated properties of the wavefunction at the zone center. Figure 3 plots the squared wavefunctions of the CB1, HH1, and HH2 states at the zone center.

From Figure 2, we can see that the electron minibands (CB1 and CB2 bands along the axis) are more dispersed than the heavy-hole minibands (HH1 and HH2 bands along the axis). This is because 1) the heavy-hole has a larger effective mass than the electron and 2) the GaSb layer which serves as a barrier layer for the electron is narrower than the InAs layer which serves as a barrier layer for the heavy-hole. As a result, the tunneling probability for the electron from one InAs layer to adjacent InAs layer is larger than that for the heavy-hole from one GaSb layer to adjacent GaSb layer. This result can be well manifested by the squared wavefunctions of the CB1, HH1, and HH2 states at the zone center, as shown in Figure 3.

Furthermore, we find the following interesting features from Figure 2 and Figure 3. 1) The fundamental band-gap, or the energy separation between the bottom of the CB1 band in the InAs layer and the top of the HH1 band in the GaSb layer, is about 10 meV (see Figure 2), which is located in the THz bandwidth since 1 THz ~ 4 meV. 2) The energy separations between CB1 and CB2 bands in the InAs layer and between HH1 and HH2 bands in the GaSb layer are larger than 100 meV (see Figure 2), which is much greater than the typical THz energy. 3) There is a considerable overlap between the electron and heavy-hole wavefunctions at the InAs/ GaSb interface (see Figure 3). These results indicate: i) the THz fundamental band-gaps can be realized in long-period InAs/GaSb type-II SLs; ii) the consider able type-II optical transitions in such SLs, namely through the inter-layer transition between the lowest conduction band in the InAs layer and the highest valence band in the GaSb layer, can be achieved in the THz bandwidth; iii) the intra-layer optical transitions cannot take place in the THz bandwidth.

In Figure 4, we show the fundamental band-gap as a function of the InAs (GaSb) layer width at a fixed GaSb (InAs) layer width. It is found that the InAs/GaSb layer widths are around 87/60, the fundamental band-gap is of the order of THz and can be tuned effectively by adjusting the InAs/GaSb layer widths. The band-gap energy decreases with increasing the InAs and/or GaSb layer widths, because the energy of the lowest electron mini band in the InAs layer decreases with increasing the InAs layer width while the energy of the highest heavy-hole miniband in the GaSb layer increases with increasing the GaSb layer width. And the band-gap energy can be tuned more effectively by varying the InAs layer width than by varying the GaSb layer width since the electron effective mass in the InAs layer is much smaller than the heavy-hole effective mass in the GaSb layer.

To understand the physical mechanism behind the application of InAs/GaSb type-II SLs as photo detectors, it is necessary to calculate the optical absorption coefficients of such SLs. We assume the radiation field is polarized along the in-plane direction of SL structure, e.g., the x-polarized light, which is the normal experimental condition for optical absorption measurements. As is known, in an undoped InAs/GaSb type-II SL, the presence of the radiation field can pump electrons in the valance band in the GaSb layer into the conduction band in the InAs layer. Such process induces photo-excited carriers whose transitions contribute mainly to the optical absorption in the SL. In general, the density of photo-excited carriers depends on the radiation intensity and frequency

and on other scattering and relaxation mechanisms. In this study, we assume that the photo-excited carrier density in undoped SLs is about per SL cell, which satisfies the condition of charge neutrality. The non-equilibrium chemical potentials (i.e.,) induced by the presence of photo-excited carriers for electrons and holes can be determined, respectively, through

(5a)

(5b)

where the band index runs over all the valence/conduction bands of the SL.

In Figure 5, we shows the dependence of optical absorption coefficient on the InAs/GaSb layer widths at T = 77 K. Due to the strong type-II optical transition (induced by the significant overlap between the electron and the heavy-hole wave functions at the InAs/GaSb interface), a sharp cut-off of THz absorption can be observed in an InAs/GaSb SL and the optical absorption is considerably strong in the bandwidth of 1 - 10 THz. The absorption coefficient can reach up to 1500 cm⁻¹ in this THz bandwidth. Such a THz broadband absorption is induced mainly by the presence of dispersed conduction bands in the SL system. Moreover, we find that with increasing the InAs/GaSb layer widths, the absorption cut-off shifts to the low-frequency regime while the absorption strength does not vary significantly. This means a more efficient THz absorption can be achieved for SLs with the larger InAs/GaSb layer widths.

Figure 6 shows the contour plots of THz band-gaps of InAs/GaSb type-II SLs. It can be seen from this figure that a constant THz band-gap can be realized in various SLs with different InAs/GaSb layer widths. To maintain a constant band-gap, an increase of the InAs layer width requires a decrease of the GaSb layer width. The physical reason is as follows. Due to the quantum-size effect, the increase of the InAs layer width leads to the lowering of the lowest electron miniband in the InAs layer and thus a smaller band-gap. Therefore, in order to maintain a constant band-gap, the GaSb layer width should be made smaller to lower the highest heavy-hole miniband in the GaSb layer. Based on the results shown in Figure 6, we conclude that for a fixed THz band-gap, it is able to design the SL structure with optimized absorption property. This is very important for the design of efficient THz photo detectors using long-period InAs/GaSb type-II SLs. Our strategy to design such optimized SL structure is as follows. With a proper choice of InAs/GaSb layer widths, the band-gap can be kept constant but the overlap between the electron and heavy-hole wave functions can be improved as the SL period is shortened. We choose four SL samples with the same band-gap of 2 THz. The InAs/GaSb layer widths for these samples are 84/95, 87/60, 91/47 and 94/42. We calculate their optical absorption spectra and show the results in Figure 7. It is found that for the fixed SL band-gap of 2 THz, the optimized optical absorption can be achieved for

the 94/42 SL sample. This is because the shortest SL structure has the largest overlap between the electron and heavy-hole wave functions and thus the strongest optical transition strength. We also study other fixed THz band-gaps, and obtain the same results for the corresponding samples.

Before closing this paper, we should point out that although long-period InAs/GaSb type-II SLs presented here have THz band-gaps and considerable THz absorption coefficient can be achieved in the corresponding SL systems, such SLs with long periodicity have less been concerned in the field of THz photo detectors, mainly because their detection efficiency (proportional to the absorption coefficient) is very low as compared to short- period InAs/GaSb SLs which can be applied as high-performance mid-infrared (MIR) photo detectors due to their large MIR absorption. Thus, for the application of long-period InAs/GaSb SLs in high-performance THz photo detectors, one may have to further improve their THz absorption coefficient. This will be considered in the future work.

4. Conclusion

In this paper, we have used the eight-band model to calculate the electronic structures of long-period InAs/ GaSb type-II SLs. It has been found that in such SLs with the InAs/GaSb layer widths around 87/60, the fundamental band-gaps are within the THz bandwidth and the electron wavefunctions overlap considerably with the heavy-hole wave functions at the InAs/GaSb interface. This implies that the considerable type-II optical transition in the THz frequency regime can be achieved in such material systems. On the basis of electronic structure results, we have employed the energy-balance equation approach derived from the Boltzmann equation to calculate the optical absorption coefficients for the corresponding SL systems. It has been demonstrated that with the proper choice of InAs/GaSb layer widths, the THz absorption coefficient can be optimized. As is known, THz region is the most scientifically rich area of the electromagnetic spectrum. The THz wave (or T-ray) technology is of great potential to impact many interdisciplinary fields such as telecommunication, biological science, pharmaceutical technology, anti-terrorist, nanotechnology, to mention but a few. The realization of T-ray sources and sensors has been an important field of research in optics and optoelectronics. The theoretical findings in the present work may shed some light on the application of long-period InAs/GaSb type-II SLs as advanced THz optoelectronic devices such as THz photodetectors.

Acknowledgements

This work was supported by the Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics (Grant No. KF201303), Ministry of Science and Technology of China (Grant No. 2011YQ130018), National Natural Science Foundation of China (Grant No. 11304316), Department of Physics of Tsinghua University, Department of Science and Technology of Yunnan Province, and by the Chinese Academy of Sciences.

References