Journal of Modern Physics
Vol.5 No.14(2014), Article
ID:49016,4
pages
DOI:10.4236/jmp.2014.514125
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
A. Georgiou
School of Physics Astronomy and Mathematics, University of Hertfordshire, Hatfield, UK
Email: a.georgiou@herts.ac.uk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2014; revised 1 July 2014; accepted 24 July 2014
ABSTRACT
We had previously obtained analytical formulae for the dipole moments and angular momenta of rotating spherical bodies. The resulting formulae were applied to the Sun, the star 78 Virginis and the Earth. The agreement of the theoretical formulae with the actual real situations is indeed remarkable. In this note we apply the same formulae to the electron and the proton, using the classical values of the radii, so no quantum mechanical treatment is considered.
Keywords:Angular Momenta, Dipole Moments, Electron, Proton

1. Introduction
The purpose of this work is to obtain analytical formulae for the dipole moments and angular momenta of the electron and the proton. For this purpose, exact solutions of the Einstein-Maxwell field equations for volume distributions of rotating charged matter are required. There are difficulties in obtaining such solutions, but these were successfully treated in detail in [1] . In addition, there are uncertainties regarding the radii of these particles, resulting in some differences between the calculated numerical values and the accepted values of the dipole moments.
2. The Electron
The mass , classical radius
, classical radius , the electric charge
, the electric charge  of the electron and the vacuum speed of light, are:
of the electron and the vacuum speed of light, are:
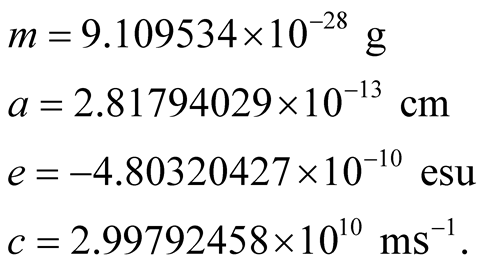 (1)
(1)
The following ratios are required:
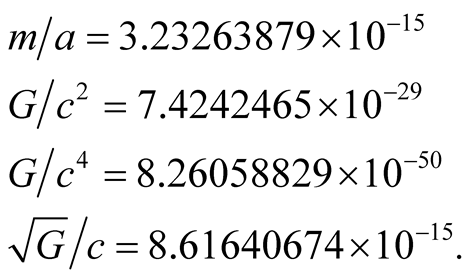 (2)
(2)
If the mass is , then there is an electric charge
, then there is an electric charge 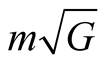 associated with
associated with 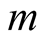 [1] . Thus, if there is an additional electric charge
[1] . Thus, if there is an additional electric charge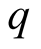 , the total charge is
, the total charge is . The value of
. The value of 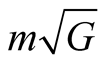 is only
is only 
and so it is negligible compared to the value of  in (1). If
in (1). If , we may therefore write for the charge
, we may therefore write for the charge 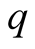 and its square
and its square ,
,
 (3)
(3)
In the Reissner-Nordstrom solution [2] , the coefficient of  in the metric, has the form given by
in the metric, has the form given by
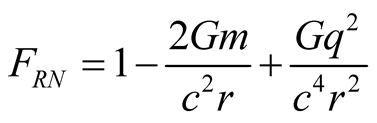 (4)
(4)
with  given by the second of (3).
given by the second of (3).
The coefficient of 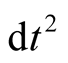 in the Kerr-Newman metric, is
in the Kerr-Newman metric, is
 (5)
(5)
with
 . (6)
. (6)
Equation (5) then, becomes
 (7)
(7)
where 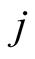 is the angular momentum per unit mass; see Equations (18)-(20) of [2] . On
is the angular momentum per unit mass; see Equations (18)-(20) of [2] . On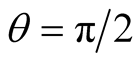 ,
, 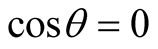 and so on
and so on 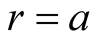 Equation (7) becomes
Equation (7) becomes
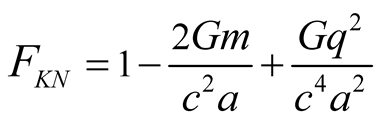 (8)
(8)
which is the same as Equation (2) of [2] (Note that in reference [2]  is used where we use
is used where we use ). It follows that instead of Equations (7)-(8) of [1] , we have for
). It follows that instead of Equations (7)-(8) of [1] , we have for 
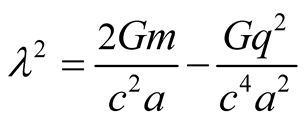 (9)
(9)
In accordance with the results of [1] , the dipole moment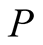 , total angular momentum
, total angular momentum 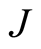 and gyromagnetic ratio are:
and gyromagnetic ratio are:
 (10)
(10)
where
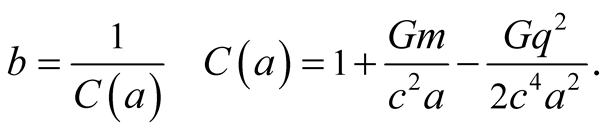 (11)
(11)
The values in (2) and (3) give for 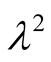 in (9) and
in (9) and 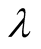
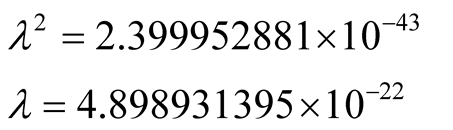 (12)
(12)
Equations (10) then give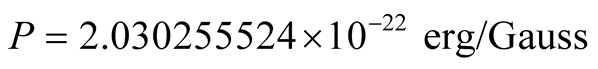 , or
, or
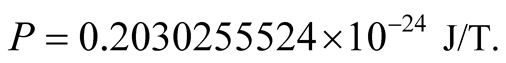 (13)
(13)
The accepted value  is
is
 . (14)
. (14)
From the second of (10), we obtain for 
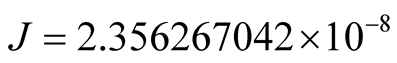 . (15)
. (15)
The gyromagnetic ratio is therefore,
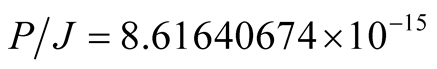 (16)
(16)
and this is precisely the value of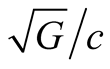 .
.
It must be noted that there are various different values for the radius of the classical electron. The value of  found is smaller than the accepted value and it depends on which radius we choose. Thus, if we use a radius with numerical value
found is smaller than the accepted value and it depends on which radius we choose. Thus, if we use a radius with numerical value
 (17)
(17)
which is 7 times larger than the classical radius of the electron and repeat the calculations, we find
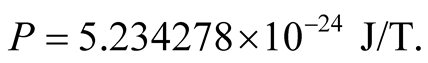 (18)
(18)
This is nearer the accepted value in (14).
It was established by Dehmelt [3] that the upper limit for the electron radius is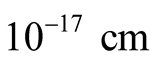 .
.
This simply implies that if 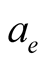 is the electronic radius, we must have
is the electronic radius, we must have . The values of the radii we used, including the “classical radius of the electron”, are much larger than this.
. The values of the radii we used, including the “classical radius of the electron”, are much larger than this.
3. The Proton
The mass, radius, electric charge and mass to radius ratio of the proton, are respectively:
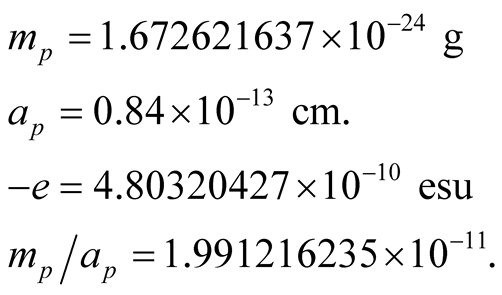 (19)
(19)
If there is an additional electric charge , the total charge will be
, the total charge will be . The value of
. The value of  is only
is only  and so it is negligible compared to the value of
and so it is negligible compared to the value of  in (1). If
in (1). If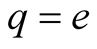 , we may therefore write for the total charge
, we may therefore write for the total charge  and its square
and its square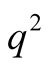 ,
,
 (20)
(20)
The same Formulae (12) for  and (10) for
and (10) for ,
,  and
and 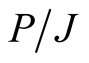 are valid, but with the proton parameters in Equations (19) instead of the electron ones. We find
are valid, but with the proton parameters in Equations (19) instead of the electron ones. We find
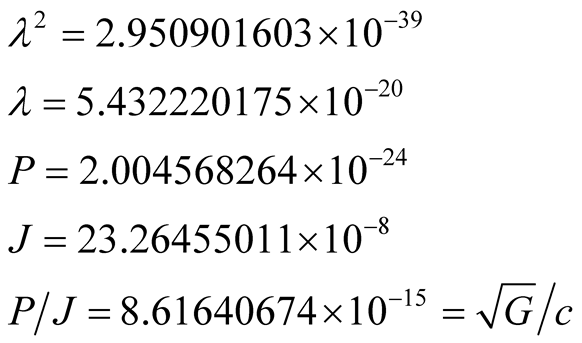 (21)
(21)
We note that the gyromagnetic ratio found in the  of Equations (21), is precisely the value of
of Equations (21), is precisely the value of .
.
In the case of the proton the value of  found is larger than the accepted value, which is
found is larger than the accepted value, which is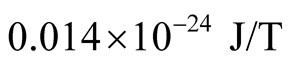 .
.
4. Conclusion
We have obtained the dipole moments angular momenta and gyromagnetic ratios of the electron and the proton using the analytical formulae developed in [1] . In the case of the electron, the value of 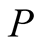 found is smaller than the accepted value, but in the proton case it is larger. If Dehmelt’s [3] deductions are valid, a complete reevaluation is necessary using our analytical Formulae (10) to find
found is smaller than the accepted value, but in the proton case it is larger. If Dehmelt’s [3] deductions are valid, a complete reevaluation is necessary using our analytical Formulae (10) to find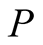 ,
, 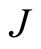 and
and . It is not possible to do this, because Dehmelt, does not give any definite values for the radii; he only states that the electron radius
. It is not possible to do this, because Dehmelt, does not give any definite values for the radii; he only states that the electron radius  should satisfy the inequality
should satisfy the inequality . But in any case, the purpose of the calculations here, is to see if the values of the known classical electron and proton radii, give the expected values of
. But in any case, the purpose of the calculations here, is to see if the values of the known classical electron and proton radii, give the expected values of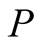 ,
,  and
and .
.
References
- Georgiou, A. (2012) Journal of Modern Physics, 3, 1301-1310.
- Blinder, S.M. (2003) Dirac’s Electron via General Relativity. PACS No: 03.50.De, 14.60.C.
- Dehmelt, H. (1988) Physical Scripta, T22, 102-110. http://dx.doi.org/10.1088/0031-8949/1988/T22/016

