Journal of Modern Physics
Vol.5 No.12(2014), Article
ID:48045,6
pages
DOI:10.4236/jmp.2014.512109
Analysis of the Metric in Quasicrystals— Linear Response in Logarithmically Periodic Solids
Antony J. Bourdillon
Ultra High Resolution Lithography (UHRL), San Jose, CA, USA
Email: bourdillona@sbcglobal.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2014; revised 8 June 2014; accepted 2 July 2014
ABSTRACT
The metric, that enables measurement of structural data from diffraction in quasicrystals, is analyzed. A modified compromise spacing effect is the consequence of scattering of periodic electromagnetic or electron waves by atoms arranged on a geometric grid in an ideal hierarchic structure. This structure is infinitely extensive, uniquely aligned and uniquely icosahedral. The approximate analytic factor that converts the geometric terms base![]() , into periodic terms modulo
, into periodic terms modulo , is
, is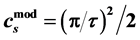 . It matches the simulated metric
. It matches the simulated metric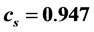 , consistently used in second (Bragg) order, over a wide scale from atomic dimensions to sixth order superclusters.
, consistently used in second (Bragg) order, over a wide scale from atomic dimensions to sixth order superclusters.
Keywords:Quasicrystals, Metric, lin-log Response, Measurement, Logarithmic, Periodic, Hierarchic, Structure

1. Introduction
The quasi-Bragg law for quasicrystals was discovered, firstly by visual inspection of the quasi-crystal diffraction pattern, and secondly by three-dimensional indexation and simulation of the pattern. The simulation is of scattering from an ideal hierarchic model for icosahedral quasicrystals [1] -[7] . The model is infinitely extensive, uniquely aligned and uniquely icosahedral. The diffraction patterns are produced by periodic waves of electromagnetic radiation or electron beams, that scatter from atoms arranged not in linear series as in crystals; but on planes that are ordered with interplanarspacings being members of the geometric series, base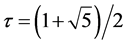 , the golden section. The scattering occurs at angles different from corresponding Bragg angles in crystals and a resulting “compromise spacing effect”
, the golden section. The scattering occurs at angles different from corresponding Bragg angles in crystals and a resulting “compromise spacing effect”  was found in the simulations. This important parameter enabled measurements of the structure to be made—not chosen as guesses [5] [8] [9] —from the diffraction data. Other differences from Bragg scattering were observed and they are sufficiently fundamental to constitute the quasiBragg law as a new law in physics. It is used to describe effects of logarithmic periodicity in three dimensions.
was found in the simulations. This important parameter enabled measurements of the structure to be made—not chosen as guesses [5] [8] [9] —from the diffraction data. Other differences from Bragg scattering were observed and they are sufficiently fundamental to constitute the quasiBragg law as a new law in physics. It is used to describe effects of logarithmic periodicity in three dimensions.
Previous explanations for the simulated values for the metric were qualitatively described. One method was to expand the cosine function used in calculations of quasi-structure factors into its regular series derived from complex exponentials: the members of both the diffraction pattern series and the cosine series expansion belong to the same geometric series ([1] Appendix A.1). This fact turns out to be related to a second explanation for simulated values for the metric: the mid terms of the geometric series, around g0, have almost half integral values [5] that distort the regularity observed in Bragg diffraction from crystals. Whereas in crystals, the structure factor is used to identify forbidden lines when the factors are zero owing to symmetries in the unit cell; in quasicrystals, we use the concept for the same purpose, but also to compensate for lack of periodicity between unit cells. We treat the solid as an infinitely large unit cell and simulate the wide variety of quasi-structure factors that are apparent in the various reflections. The method depends on three dimensional indexation, and also on the model of structure factor calculation in crystals. Now we are able, analytically, to clarify the quantitative result for the metric obtained in the simulations. The metric is the key to understanding any measurement dependent on diffraction in quasicrystals.
2. Linear and Logarithmic Periodicities
The chief justification for the present analysis is the simple, complete and systematic simulation of the principal diffraction patterns [1] -[7] displayed by icosahedral i-Al6Mn [10] . These patterns depend on the quasi-Bragg law:
 , (1)
, (1)
where 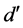 is a corrected quasi-interplanar spacing
is a corrected quasi-interplanar spacing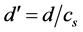 ; with compromise spacing effect cs that is discovered to be the same for all quasi-structure factors; and where the quasi-Bragg angle
; with compromise spacing effect cs that is discovered to be the same for all quasi-structure factors; and where the quasi-Bragg angle  differs from the Bragg angle θ in crystals, chiefly because of the multiple interplanarspacings that, in quasicrystals, contribute to each diffracted beam1. The incident radiation wavelength is λ, and m and n are orders. Every variable except wavelength differs in the original Bragg law:
differs from the Bragg angle θ in crystals, chiefly because of the multiple interplanarspacings that, in quasicrystals, contribute to each diffracted beam1. The incident radiation wavelength is λ, and m and n are orders. Every variable except wavelength differs in the original Bragg law:
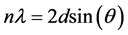 (2)
(2)
and even the constant 2 transforms to unity. The reason for this will be found in the following analysis. Equation (1) can be reformulated in the conventional way by writing, in zeroth quasi-Bragg order2,  , for quasiMiller indices
, for quasiMiller indices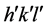 ,
,
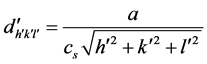 (3)
(3)
using for axes the cubic sub-group of the icosahedral point group symmetry, where a is the diameter of the Al atom that is equal to the side length of the icosahedral unit cell. (In calculations, it was convenient to use this number as the unit of length, the icosahedral unit). The quasi-Miller indices are three dimensional. A key concept is the compromise spacing effect and there are various ways in which it can be described. It was first measured in simulations of the quasi-structure factor calculated from the following formula that is derived from the formula commonly used for calculating structure factors from unit cells in crystal physics:
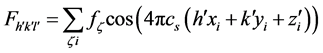 (4)
(4)
summed over atoms having scattering factors fζ for ζ = Al or Mn in this case, and with atomic positions xi, yi, zi. The formula applies to the centro-symmetric, hierarchic model in second Bragg-order where it maximizes at cs. The results demonstrate negligible values for Bragg structure factors where cs = 1, and for higher Bragg orders (n > 2) that are generally not observed in quasicrystals. The quasi-Bragg angle is adjusted by 5.3% so as to correspond, through Equation (1), with cs (whether simulated or derived as below). It was found that the same cs applies to all diffracted beams, and this leads to the generic explanation that follows. What we have is a periodic incident beam that is scattered by a set of atoms on a geometric grid into diffracted beams with quasi-Miller indices  (Figure 1). Being geometric, the atomic interplanarspacings are members of the series
(Figure 1). Being geometric, the atomic interplanarspacings are members of the series![]() , where the spacings are describable in three dimensions. In electron diffraction, where scattering angles are small,
, where the spacings are describable in three dimensions. In electron diffraction, where scattering angles are small, 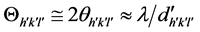 , similar to the corresponding scattering angle in grating optics. The metric cs is most easily understood as mediating the two series, linear and geometric, as we shall see.
, similar to the corresponding scattering angle in grating optics. The metric cs is most easily understood as mediating the two series, linear and geometric, as we shall see.
Previously we have noticed three features in simulations of the quasi-structure factors:
a) the diffraction is in second Bragg order [5] [6] ;
b) the diffracting angle is less than the equivalent Bragg angle. The difference is the compromise spacing effect or metric.
c) The terms in the quasi-scattering angle are geometric because of the logarithmic grid on which the atoms in the model reside (Equation (4)). Likewise the terms in the cosine expansion are members of a geometric series [1] .
What is needed is the factor that converts those geometric terms in Equation (4) that result from the locations of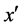 ,
, 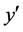 , and
, and 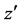 on a logarithmic grid base
on a logarithmic grid base![]() , into the corresponding series that is periodic in space common to the incident and diffracted beams, i.e. modulo
, into the corresponding series that is periodic in space common to the incident and diffracted beams, i.e. modulo![]() . That factor is
. That factor is  (see Table 1).
(see Table 1).
The factor can be seen to convert the regular series expansion of the cosine function, its argument forming the base of a geometric series. We can, in consequence, collate items a, and b to produce a modified compromise

Figure 1. Schematic illustration of scattering of a periodic incident wave (top), wavelength λ, by a cluster of icosahedral i-Al6Mn atoms on a logarithmic grid (center), onto a geometric diffraction pattern (bottom). Near center, the (100) axis is normal to the plane shown, with (010) horizontal. Populations of Al atoms are shown above the horizontal abscissa, with Mn below it. At highest contrast in the two beam condition [12] , a quasi-Bloch wave is superposed on these populations and the overlap (Σ) is maximum [4] . The wave illustrates lin-log response, where high resolution transmission microscopy does not image atoms [1] .
Table 1. Trigonometric values for the geometric series demonstrate periodicity given by the inclusion of the conversion factor π/τ in column 7. Notice the significant result on line 7. Negative values are red; significant values bold.
spacing effect,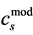 . This new convention has the disadvantage that it loses closeness to Bragg values for spaces, angles, wavelengths and indices (~5.3% under the simulated convention where the metric was ~
. This new convention has the disadvantage that it loses closeness to Bragg values for spaces, angles, wavelengths and indices (~5.3% under the simulated convention where the metric was ~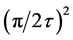 ); but the new convention has the convenience of explaining the common reasons for the two effects that had previously been described separately. Both effects had the same origin in maximization of the quasi-structure factors within the constraints of forbidden Bragg orders—forbidden that is in both observed diffraction patterns, and in corresponding calculations. Notice that, under the old convention the simulated
); but the new convention has the convenience of explaining the common reasons for the two effects that had previously been described separately. Both effects had the same origin in maximization of the quasi-structure factors within the constraints of forbidden Bragg orders—forbidden that is in both observed diffraction patterns, and in corresponding calculations. Notice that, under the old convention the simulated 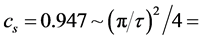
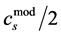 , where
, where 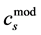 describes a new approximate convention that is now derived analytically. The new convention supplies the factor that converts geometric terms, with logarithmic periodicity in the cosine expansion, to periodic terms modulo
describes a new approximate convention that is now derived analytically. The new convention supplies the factor that converts geometric terms, with logarithmic periodicity in the cosine expansion, to periodic terms modulo![]() . This is the factor that mediates the periodic incident beam with the geometrically arranged atoms. It offsets the simulated quasi-Bragg angle from the corresponding crystal Bragg angle.
. This is the factor that mediates the periodic incident beam with the geometrically arranged atoms. It offsets the simulated quasi-Bragg angle from the corresponding crystal Bragg angle.
How does this conversion factor 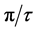 cause the argument of Equation (4) to become periodic? The answer is that every term in the inner bracket of the argument in Equation (4) contains some power of
cause the argument of Equation (4) to become periodic? The answer is that every term in the inner bracket of the argument in Equation (4) contains some power of ![]() and these values are periodic in logarithmic space [1] :
and these values are periodic in logarithmic space [1] :
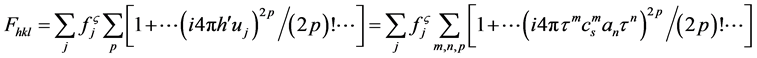 (5)
(5)
where an atomic location 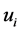 is equal to some sum over
is equal to some sum over  [1] , with
[1] , with 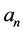 integral. In order to link to the periodic incident wave, the geometric series is made periodic in real space by replacing
integral. In order to link to the periodic incident wave, the geometric series is made periodic in real space by replacing ![]() by
by![]() , i.e. by applying the metric. Our compromise spacing effect cs expresses the difference here from Bragg diffraction for a periodic crystal lattice. In the execution of Equation (5), the quasi-structure factor is squared to realize its observed intensity [11] and this gives the value for
, i.e. by applying the metric. Our compromise spacing effect cs expresses the difference here from Bragg diffraction for a periodic crystal lattice. In the execution of Equation (5), the quasi-structure factor is squared to realize its observed intensity [11] and this gives the value for 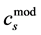 shown in the previous paragraph (since
shown in the previous paragraph (since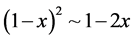 ,
, ). The value includes higher order terms in the cosine series and so the simulated value is the more accurate. The modified metric can be used in an analytical modification of Equation (4):
). The value includes higher order terms in the cosine series and so the simulated value is the more accurate. The modified metric can be used in an analytical modification of Equation (4):
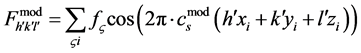 (6)
(6)
Meanwhile the quasi-Bragg law ensures that corresponding adjustments are made in interplanarspacings and quasi-Bragg angles. Though the two conventions using cs and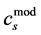 , are approximately equivalent, the reader may find the older one is more intuitive because closer to Bragg methods in crystals.
, are approximately equivalent, the reader may find the older one is more intuitive because closer to Bragg methods in crystals.
Notice that the logarithmic grid is not a simple concept. There are several ways to describe it. One is ostensive: it is the grid that sites the atoms in the hierarchic Al6Mn structure [6] . A second way is through the logarithmic quasi-reduced zone scheme in the quasi-Brillouin zone representation of energy bands in Al6Mn [2] . A third way is a description of overlapping grids with origin repeating on principal grid points. An example of this grid is used in the indexation of the two-fold pattern in Al6Mn [6] . Yet another example is illustrated, in one dimension, near the center of figure 1. This grid contrasts with a crystalline lattice.
The quasi-structure factor simulation constitutes, in itself, a simple demonstration of quasi-Bragg diffraction and this new analytical explanation now confirms it. As a subsidiary illustration, and to conserve similarities to Bragg diffraction, we show the effect of the conversion factor on various trigonometric values that were previously used in the quasi-structure factor calculations derived from Equation (4). It is evident in Table 1 that the inclusion of the factor 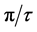 causes the trigonometric values to become periodic. This regularity matches the simulation results that demonstrate positive interference at the quasi-Bragg angles,
causes the trigonometric values to become periodic. This regularity matches the simulation results that demonstrate positive interference at the quasi-Bragg angles,![]() . The interpretation is consistent with simulations on truncated clusters and superclusters of various sizes [4] [6] [7] . In these, the number of scattering atoms correlates with the width, in scattering angle, of the calculated quasi-structure factor profiles. More generally, the table demonstrates the analytical importance of the metric. To mark the result, terms greater than 0.5 are shown in bold font in the table, and negative values are shown in red.
. The interpretation is consistent with simulations on truncated clusters and superclusters of various sizes [4] [6] [7] . In these, the number of scattering atoms correlates with the width, in scattering angle, of the calculated quasi-structure factor profiles. More generally, the table demonstrates the analytical importance of the metric. To mark the result, terms greater than 0.5 are shown in bold font in the table, and negative values are shown in red.
Further explanations are more or less obvious. The “third bright ring” of diffracted beams away from zero order, that is evident in Shechtman’s and other data—especially when specimen films are thin—is due to the index , where the value in column 7 is larger than those of its neighbors. This feature in Table 1 is consistent with our adopted method of indexation [5] [6] and confirms it. Most importantly, the calculated quasi-structure factors match experimental data very well indeed. Moreover, these general phenomena show that the Ewald sphere construction that applies rigorously in X-ray diffraction from crystals—but rather weakly in electron diffraction —requires re-analysis in quasicrystals. This marks territory for further experiment and research.
, where the value in column 7 is larger than those of its neighbors. This feature in Table 1 is consistent with our adopted method of indexation [5] [6] and confirms it. Most importantly, the calculated quasi-structure factors match experimental data very well indeed. Moreover, these general phenomena show that the Ewald sphere construction that applies rigorously in X-ray diffraction from crystals—but rather weakly in electron diffraction —requires re-analysis in quasicrystals. This marks territory for further experiment and research.
Moreover, with the understanding given below for cs and , it is reasonable to speculate on possible uses that might be made of precise measurements. If the metric turns out to be minutely sensitive to disorder in a quasicrystal, then precise measurement of cs could be used in defect analysis, along with dark field imaging [3] . Careful calibration would be needed to make use of the small changes.
, it is reasonable to speculate on possible uses that might be made of precise measurements. If the metric turns out to be minutely sensitive to disorder in a quasicrystal, then precise measurement of cs could be used in defect analysis, along with dark field imaging [3] . Careful calibration would be needed to make use of the small changes.
3. Discussion
Hitherto, it has seemed that the metric is a fortuitous factor that mediates logarithmic space with real space. However, the calculations on Table 1, especially column 7 line 7, when combined with the periodic regularization of the column, make it most improbable that the link is fortuitous. It is now possible to see that the link is precisely constrained. This appears from the series expansion of the cosine function. The metric causes the expansion in terms of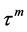 , to convert to the same series expansion, but in terms of
, to convert to the same series expansion, but in terms of![]() . The metric therefore converts the logarithmic series contained in the cosine function to a function modulo
. The metric therefore converts the logarithmic series contained in the cosine function to a function modulo![]() . In this conversion the compromise spacing effect is applied together with the simulated “second Bragg order”. In the analytic form,
. In this conversion the compromise spacing effect is applied together with the simulated “second Bragg order”. In the analytic form, 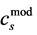 is applied to quasi-structure factor calculations in first (Bragg) order; in the more accurate simulated form, cs had been applied in second (Bragg) order through a slightly different formula. It was once more common for the solid state to contribute to general physics, as in the example of statistical physics; the linear response to logarithmically spaced scatterers is a new example. Science should be made a simple as possible but not simpler: the log-lin metric can no longer be avoided.
is applied to quasi-structure factor calculations in first (Bragg) order; in the more accurate simulated form, cs had been applied in second (Bragg) order through a slightly different formula. It was once more common for the solid state to contribute to general physics, as in the example of statistical physics; the linear response to logarithmically spaced scatterers is a new example. Science should be made a simple as possible but not simpler: the log-lin metric can no longer be avoided.
4. Conclusion
The compromise spacing effect and metric, in quasicrystal diffraction, occur under the quasi-Bragg law. Analysis shows that the metric is due to the conversion factor  that mediates scattering of a periodic beam by atoms lying on a geometric grid. The metric is explained by the factor that converts geometric series (base
that mediates scattering of a periodic beam by atoms lying on a geometric grid. The metric is explained by the factor that converts geometric series (base![]() ) in atomic locations, to the geometric terms in the series expansion of the cosine (modulo
) in atomic locations, to the geometric terms in the series expansion of the cosine (modulo![]() ). The factor,
). The factor, 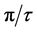 , is consistent with, and confirmed by, prior detailed and systematic simulation of quasi-structure factors. The quasi-Bragg law adapts corresponding adjustments to interplanarspacings and quasi-Bragg angles. When logarithmic periodicity is discovered in one part of physics, it is expected in others.
, is consistent with, and confirmed by, prior detailed and systematic simulation of quasi-structure factors. The quasi-Bragg law adapts corresponding adjustments to interplanarspacings and quasi-Bragg angles. When logarithmic periodicity is discovered in one part of physics, it is expected in others.
References
- Bourdillon, A.J. (2014) Journal of Modern Physics, 5 488-496. http://dx.doi.org/10.4236/jmp.2014.56060
- Bourdillon, A. J. (2009) Solid State Communications, 149, 1221-1225. http://dx.doi.org/10.1016/j.ssc.2009.04.032
- Bourdillon, A.J. (2013) Micron, 51, 21-25. http://dx.doi.org/10.1016/j.micron.2013.06.004
- Bourdillon, A.J. (2011) Logarithmically Periodic Solids. Nova Science, New York.
- Bourdillon, A.J. (2012) Metric, Myth and Quasicrystals. UHRL, San Jose.
- Bourdillon, A.J. (2009) Quasicrystals and Quasi Drivers. UHRL, San Jose.
- Bourdillon, A.J. (2010) Quasicrystals’ 2D Tiles in 3D Superclusters. UHRL, San Jose.
- Steurer, W. (2004) Zeitschrift für Kristallographie, 219, 391-446. http://dx.doi.org/10.1524/zkri.219.7.391.35643
- Steurer, W. and Deloudi, S. (2008) ActaCrystallographica, A64, 1-11. http://dx.doi.org/10.1107/S0108767307038627
- Shechtman, D., Blech, I., Gratias, D. and Cahn, J.W. (1984) Physical Review Letters, 53, 1951-1953. http://dx.doi.org/10.1103/PhysRevLett.53.1951
- Cullity, B.D. (1978) Elements of X-Ray Diffraction. 2nd Edition, Addison-Wesley, Addison.
- Hirsch, P., Howie, A., Nicholson, R.B., Pashley, D.W. and Whelan, M.J. (1977) Electron Microscopy of Thin Crystals. Krieger.
Two Tutorial Endnotes Added in Proof
While in crystals, an allowed line has non-zero structure factor when 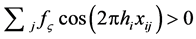 summed (by the repeated subscript convention) over dimensions i, j = 1, 2, 3 in a unit cell; in quasicrystals, allowed lines have quasi-structure factors
summed (by the repeated subscript convention) over dimensions i, j = 1, 2, 3 in a unit cell; in quasicrystals, allowed lines have quasi-structure factors 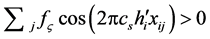 where
where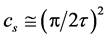 , and simulated quasi-structure factors match experimental intensities. It is interesting that
, and simulated quasi-structure factors match experimental intensities. It is interesting that 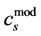 occurs in the second term of the expansion of
occurs in the second term of the expansion of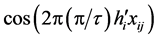 .
.
NOTES
![]()
1By contrast, Bragg’s law gives a unique interplanar spacing for each specular diffracted beam.
2This formula resembles a corresponding formula for the first Bragg order, n = 1; but the orders in quasicrystals extend past zero to m = −∞ (the straight through beam). The value described, in Equation (3), is for the quasicrystal zero order, where the corresponding interplanar spacing is the side length of the icosahedral unit cell. In i-Al6Mn, this length is the diameter of the Al atom.


