Received 7 May 2014; revised 2 June 2014; accepted 25 June 2014

ABSTRACT

The nonlinear affine Goldstone model of the emergent gravity, built on the nonlinearly realized/ hidden affine symmetry, is concisely revisited. Beyond General Relativity, the explicit violation of general invariance/relativity, under preserving general covariance, is exposed. Dependent on a nondynamical affine connection, a generally covariant second-order effective Lagrangian for metric gravity is worked out, with the general relativity violation and the gravitational dark matter serving as the signatures of emergence.

Keywords:

Spontaneous Symmetry Breaking, Nonlinear Realizations, Emergent Gravity, General Relativity Violation, Dark Matter

1. Introduction

It is widely accepted nowadays that General Relativity (GR) may be just (a piece of) an effective field theory of gravity to be ultimately superseded at the high (conceivably, as high as the Planck scale) energies by a more fundamental/underlying theory. At that, the conventional metric gravity could cease to be a priori existent, but, instead, would become an emergent/induced phenomenon. A lot of the drastically different approaches towards the emergence of gravity and space-time is presently conceivable¹. In this paper, we work out an approach to the goal treating gravity as an affine Goldstone phenomenon in the effective field theory framework.

Typically, as a herald of an unknown high-energy theory there serves at the lower energies a nonlinear model. Being based on a nonlinearly realized/hidden symmetry, remaining linear on an unbroken subgroup, such a model could encounter in a concise manner for the spontaneously/dynamically broken symmetries of the fundamental theory. Inevitably, this occurs at the cost of more uncertainty and a partial loss of content. For the global continuous internal symmetries, the nonlinear model framework was developed in [3] [4] . This approach proved to be extremely useful for studying, e.g., the so-called chiral model and played an important role in the advent of QCD as the true fundamental theory of strong interactions.

One might thus naturally expect that in the quest for an underlying theory of gravity GR should first be substituted by a nonlinear model. As such a model for gravity, aimed principally at reconstructing GR, there was originally proposed the model based on the nonlinearly realized/hidden affine symmetry, remaining linear on the unbroken Poincare subgroup [5] [6] ². In the context of emergence of gravity and space-time, the model was elaborated in [7] [8] . At that, reproducing GR the model may well include the GR violation [9] ³. To this end, one should envisage in a field theory two kinds of fields—the dynamical/relative and nondynamical/absolute ones—and, respectively, two kinds of the diffeomorphism symmetries. First, the kinematical symmetry—the covariance restricts the mathematical form of the theory. Second, the dynamical symmetry—the general invariance/relativity serves as a gauge symmetry for gravity determining the physical content of the latter [10] ⁴. In GR, without nondynamical fields, these notions coincide, both being the general ones. But beyond GR, in the presence of nondynamical fields, the notions differ. For consistency, the general covariance should better be preserved. On the other hand, the general invariance/relativity violation may well take place, serving as a source of the gravitational dark matter (DM). In the simplest case, such a scenario was worked out for the well-posed theory of gravity minimally violating GR to the unimodular relativity, with the scalar-graviton DM [9] [10] . Extending this scenario to other types of the GR violation and gravitational DM would thus be urgent.

In this paper, the model of emergent gravity based on the nonlinearly realized/hidden affine symmetry—the nonlinear affine Goldstone model—is systematically revisited. To allow for the GR violation, two kinds of co- ordinates—the absolute/background and relative/observer’s ones—are envisaged. A generally covariant second- order effective Lagrangian for the emergent metric gravity, dependent on a nondynamical affine connection, is consistently worked out in the most general fashion, with a limited version discussed in more detail. The model is proposed as a prototype for the emergent gravity and space-time, with the GR violation and the gravitational DM serving as the signatures of emergence. In Section 2, the nonlinear realizations are applied in the context of emergent gravity on an arbitrary nondynamical affine background. In Section 3, an effective Lagrangian of emergent metric gravity is worked out and discussed. Appendix A shortly describes the general techniques of nonlinear realizations for the spontaneous/dynamical symmetry breaking. Appendix B presents a short compendium of conventions and notations.

2. Nonlinear Realizations and Emergent Gravity

2.1. Gravity as an Affine Goldstone Phenomenon

In the case at hand in the paper, an underlying theory of gravity is to be originally invariant under the global affine symmetry group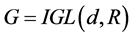, 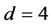⁵. Eventually, the symmetry spontaneously/dynamically brakes down to the Poincare one, assumed to be exact:

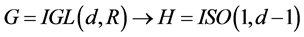. (1)

A putative mechanism of such a breaking is beyond the scope of the nonlinear model. According to general theory (see, Appendix A), the breaking results in the nonlinear realization of the affine symmetry on the coset space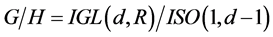, with the 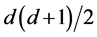-component coset elements. The Goldstone boson of the respective nonlinear realization is to be treated as a primary gravity field. To consistently apply the nonlinear realization technique to such a global external symmetry, a two-stage procedure is to be implemented, starting from a flat affine background and extending then onto a curved one.

2.2. Flat Affine Background

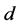First, let be a -dimensional homogeneous space, with the affine group of motions,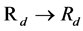. By default, admits the globally affine coordinates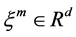, 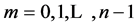⁶, undergoing the affine transformations:

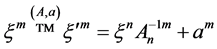, (2)

with the arbitrary constant parameters 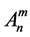and for the (reversible) linear deformations and translations, respectively⁷. This space will serve as the representation one for constructing the nonlinear model. In accord with the general formalism, there are two modes for realization of the hidden affine symmetry: the nonlinear and linearized ones.

2.2.1. Pseudo-Symmetric Nonlinear Realization

A coset element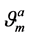, , may uniquely be chosen to be pseudo-symmetric, i.e.,

. (3)

(at least in a suitable neighborhood of, where this condition is evidently fulfilled). Here, (and) is the invariant under Minkowski symbol, by which the globally Lorentzian indices, , etc., are manipulated. Under the coset element should transform nonlinearly as

, (4)

with chosen so to retain the pseudo-symmetry after action of. At that, due to there automatically fulfills the linearity condition for any ⁸. Present the symmetric Lorentz tensor in terms of a symmetric tensor as, where, e.g., , etc. With serving as a classification group, one can treat, with independent components, as a tensor Goldstone boson emerging under breaking the global affine symmetry to the Poincare one.

2.2.2. Locally Lorentzian Linear Representation

The affine Goldstone model gets simplified with the nonlinear realization being linearized in terms of a ‑component frame-like field, (and its inverse). The field transforms under as

(5)

(and likewise for), modulo an arbitrary satisfying, with the invariant. Due to invariance under, with the local parameters, the number of the independent components remains in fact the same. Explicitly, one can impose a Lorentz gauge by projecting so that becomes pseudo-symmetric. Thus, the two realization modes, the nonlinear and linearized ones, are equivalent. However, the linear representation may be more advantageous due to grasping all the equivalent nonlinear realizations.

Restricting ourselves to the pure gravity, introduce the generic action element produced by an infinitesimal neighborhood of a reference point as follows:

, (6)

with being invariant relative to. For the pure gravity, the field may be converted into the symmetric Lorentz-invariant second-rank affine tensor with independent degrees of freedom:

. (7)

In particular, one has. This tensor may eventually be treated as the emergent metric

being absent prior to the affine symmetry breaking. Transforming the result to the arbitrary curvilinear coordinates on and integrating over one would get the nonlinear model of gravity on the flat affine background. To account for a more general topology, one should go over to a curved affine background, with the action element given by Equation (6) used as a local flat counterpart.

2.3. Curved Affine Background

Let now be a -dimensional differentiable “world” manifold marked with some “observer’s” coordinates, ⁹. Let be moreover endowed with a nondynamical affine connection, free of torsion,. Such a background affine “texture” is to be formed by an underlying theory on par with the affine symmetry breaking. In a vicinity of a fixed, but otherwise arbitrary point the connection may be decomposed as follows

, (8)

where is the background curvature tensor in the reference point. In a patch around, choose on some coordinates (having the inverse) so that conventionally

, (9)

where and. Differentiating the reversibility relations and one gets and. More particularly, adjust the coordinates as follows:

, (10)

implying

. (11)

In view of Equation (9) one thus gets. Moreover, in view of Equation (8) in coordinates one has

. (12)

The manifold looking in the coordinates approximately flat around, call such coordinates the locally affine ones attached to the point, with and being the respective locally affine frames. In these coordinates, project a patch of around onto the representation space (associating the latter

with the tangent space in) through. This maps in the leading

approximation the action element given by Equation (6) from onto. Transform then the local result around from coordinates to the arbitrary observer’s coordinates by means of substitutions

, and, with frames and. Integrating finally over

one gets the generic gravity action (redefining) as follows:

.(13)

Evidently, the locally Lorentzian frame satisfies the reversibility relations and. Due to the frame transforms under the diffeomorphisms modulo an arbitrary as

. (14)

(and likewise for). The action given by Equation (13), as originated from Equation (6), is to be invariant relative to the local Lorentz transformations, being at the same time generally covariant. At that, the locally Lorentzian frame is to be treated as the dynamical one, while the background affine connection as nondynamical. Otherwise, under extremizing, the background connection should not be varied,. Under the requirement of the background-independence, the action would preserve the general diffeomorphism invariance/relativity. In the case of the residual dependence on the background, the action, though retaining the general covariance, violates, partially or totally, the general invariance/relativity.

Emergent Metric

Restricting himself by the pure gravity one can choose as an independent variable for gravity, instead of the Lorentzian frame, its bilinear Lorentz-invariant combination

. (15)

with ¹⁰ At that, the frame, of which is composed, though being the primary

gravity field, manifests itself explicitly only in interactions with matter (omitted here). The tensor field may be treated as an emergent metric. It is the emergence of metric which converts a background manifold with an affine connection into the true space-time, the latter becoming in a sense emergent, as well¹¹.

3. Violated Relativity and Dark Matter

3.1. Affine Symmetry

Building the real nonlinear model starts out from in the globally affine coordinates. To construct the Lagrangian dependent on the affine tensor and its derivatives construct first the Christoffel-like affine tensor

. (16)

A derivative of may uniquely be expressed through a combination of (and v.v.). By means of the latter, one can construct the Riemann tensor, the Ricci tensor and the Ricci scalar. Altogether, one can construct on the generic affine-invariant second-order effective Lagrangian for gravity

. (17)

with the partial bilinear in contributions as follows:

. (18)

For completeness, there is included into a constant. The parameter is the Planck mass, with being the Newton’s constant, and, , are the dimensionless free parameters. The presented terms exhaust all the bilinear in second-order ones admitted by the affine symmetry, with no prior preference among them¹². Transforming the results to the curvilinear coordinates on one would arrive at a generally covariant theory of gravity on a flat affine background. However, this is no more than a limited version of a more general case (see, further on).

3.2. General Covariance

Let us then map the above results from onto, first, in the locally affine coordinates around through the identical substitution and then in the arbitrary observer’s coordinates around (using for the counterpart of Equation (9) supplemented by Equation (11)). Altogether,

we get the relation

, (19)

where conventionally (with)

. (20)

is the Christoffel connection corresponding to metric. Altogether, the most general second-order generally covariant effective Lagrangian for the emergent metric gravity is given by Equation (17), with¹³

(21)

dependent on the generally covariant tensor

. (22)

The background-independent term corresponds to GR with a cosmological constant, while the background-dependent ones, , to the GR violation. The theory of gravity with the GR-violating effective Lagrangian given by Equations (17), (21) and (22) may be referred to as Violated Relativity (VR). Most generally, it depends on the nondynamical functions besides the five constant Lagrangian parameters ¹⁴.

3.3. Gravitational DM

Varying the gravity action with respect to, under fixed, we get the vacuum gravity field equations in a generic form as follows:

. (23)

Here are the generally covariant contributions to the equations due to:

, (24)

with and designating a total variational derivative. The r.h.s. of Equation (23) may formally be treated as a covariantly conserved, , canonical energy-momentum tensor of the gravitational DM due to the GR violation. An affine texture of space-time due to, resulting in such a phenomenon, signifies ultimately the gravity and space-time as emergent.

3.4. Limited GR Violation

Generally, the phenomenological study of VR is rather cumbersome. To simplify it as much as possible, consider the formal limit corresponding to the flat affine background in the globally affine coordinates. The various observations being in reality fulfilled in the different coordinates, it is practically impossible for an observer to guess/use the unknown globally affine coordinates ab initio. In the lack of this knowledge, one should start from suitable observer’s coordinates, assuming some, to eventually reveal, with the help of observations, the globally affine coordinates (independent of any reference point), so that. According to Equation (9), one should have in this case the restriction

, (25)

Here and are the frames relating the distinguished globally affine coor

dinates and the arbitrary observer’s ones in terms of the nondynamical generally covariant scalar fields (having the inverse). This is the least set of free functions to consistently account for the GR violation, under preserving general covariance. The topology of the affine background, flat vs. curved, is thus not a pure theoretical question but becomes, in principle, liable to observational verification¹⁵. Anyhow, the flat affine background determined by Equation (25) could be treated, in a space-time region, as an approximation to a curved affine background determined by a regular ¹⁶.

3.5. Unimodular Relativity

For one has

, (26)

where. Moreover, if the affine background is flat, one gets in view of Equation (25):

. (27)

Thus under this limitation one has

, (28)

where

, (29)

with

. (30)

The field, determined by the ratio of the two scalar densities of the same weight, behaves like a generally covariant scalar. The nondynamical field being a unimodular scalar, the theory with only (in addition to) may for uniformity be referred to as Unimodular Relativity (UR), with the scalar graviton serving as DM [9] [10] . The scalar graviton proves now to be nothing but a Goldstone boson corresponding to the hidden dilatation symmetry¹⁷. Besides, the so-called “modulus” acquires the clear-cut physical meaning^18,19. To qualitatively compile with the astrophysical data on the galaxy anomalous rotation curves due to the dark halos, there should fulfill, with being an asymptotic rotation velocity. To tame phenomenologically the possible unwanted properties of the gravitational DM, a hierarchy of the GR violations may be envisaged, with GR substituted first by UR and ultimately by VR.

4. Conclusion

The nonlinear affine Goldstone model may provide a prototype for the emergent gravity, with the GR violation and the gravitational DM serving as the signatures of emergence. The proper account for a nondynamical affine connection, missing in GR, proves to be crucial. The main outcome of the model is the effective Lagrangian for the emergent metric gravity given by Equations (17), (21) and (22) (supplemented in the limited version by Equation (25)). Resulting in VR, the model widely extends the phenomenological horizons beyond GR, with the possible substitution of GR first by UR and then by VR. In an ultimate theoretical perspective, the model may, hopefully, serve as a guide towards a putative underlying theory of gravity and space-time.

5. Appendices

5.1. Spontaneous Symmetry Breaking and Nonlinear Realizations

Let us shortly recapitulate the techniques of the nonlinearly realized/hidden symmetries. Let a global continuous internal symmetry, with the dimension, be spontaneously/dynamically broken, , to some ‑dimensional subgroup. Let be the respective -dimensional (for definiteness, left) coset space consisting of the (left) coset elements. Then any group element admits a unique (at least in a vicinity of unity) decomposition, with and. Henceforth under the action of a group element, one should get. The group thus acts on by means of the transformations dependent, generally, on (henceforth the term nonlinear). Mapping a flat space onto, , defines on a coset-valued field,. This induces a nonlinear realization of on. Restricted by the unbroken subgroup, i.e., under, the nonlinear realization of is to be a usual linear representation of, , with and. Putting, , , with being the broken generators of, one can treat the ‑component field as a Goldstone boson emerging under the global symmetry breaking. Due to the isomorphism (at least in a vicinity of unity), one can substitute a coset element by its equivalence class obtained from through the (right) multiplication by an arbitrary. At that, the nonlinear realization gets linearized as, modulo an arbitrary independent of. And v.v., fixing a gauge for results in imposing the restrictions on and choosing thus a nonlinear realization. Hence, being equivalent to the linear representation, all the nonlinear realizations for breaking are equivalent among themselves in the effective field theory sense. At that, the linearization of a hidden symmetry may be more advantageous as embodying on par all the equivalent nonlinear realizations.

5.2. Conventions and Notations

For convenience, let us present a short compendium of conventions and notations used in the paper. For generality, the dimension of space-time is assumed, with the temporal-spacial signature. is a representation space/a flat affine background covered with the globally affine coordinates. The indices undergo the affine transformations through.

is a coset field on. The indices undergo the global Lorentz transformations. is a curved world manifold covered with the observer’s coordinates. are the world indices undergoing the diffeomorphism transformations through produced by the general coordinate changes. is a nondynamical background affine connection on. are the distinguished locally affine coordinates on, attached to an

arbitrary point, with. is the respective locally affine frame. is the dy-

namical Christoffel connection on, corresponding to the emergent metric. The metric is constructed from a pair of the locally Lorentzian frames treated as the true gravity field on. The indices undergo the local Lorentz transformations.

References

NOTES

¹For recent surveys of the emergent gravity and space-time, see, e.g. [1] [2] .

²For a fiber bundle formalism, cf. [7] .

³To characterize such a phenomenon, the term “general covariance violation” used in [9] is to be more appropriately substitutes by the “general invariance/relativity violation” [10] used in what follows.

⁴For a discussion of the general covariance vs. general invariance, cf. also [11] .

⁵The following consideration is formally independent of.

⁶Being here just a notation, the index is understood to subsequently compile with the unbroken Lorentz subgroup.

⁷Remaining unbroken, the translation part of the symmetry is omitted in what follows.

⁸Moreover, the dilatations are represented linearly, too, with the trivial compensating factor,.

⁹The index here is just a notation acquiring the physical meaning after the emergence of metric.

¹⁰By this token, one can use the convectional relation, etc.

¹¹the same vein, one could formally consider other patterns of the affine symmetry breaking, , , resulting in the same number of the affine Goldstone bosons, with the temporal-spatial signature of the emergent metric to be eventually selected [8] . For, cf., e.g. [12] .

¹²On the affine symmetry reason, one could add two more linear terms, and, which however may be expressed though the rest of the terms modulo surface contributions.

¹³The terms without derivatives of, as well as the extra factors given by the powers of, are forbidden by the hidden affine symmetry.

¹⁴Treating as the small perturbations and as the leading term, one can extend the latter by the higher-order generally covariant contributions.

¹⁵Under restriction ab initio by GR, the type of the affine background, flat or curved, would superficially seem irrelevant.

¹⁶A limiting generally noncovariant case corresponding here, in this paper, to GR violation with, and was elaborated, irrespective of DM, in [13] .

¹⁷Such a specific dilaton in disguise, representing a compression gravity mode in metric, may be called the “systolon” [10] .

¹⁸It proves that the unknown modulus may be hidden into taken as an independent field variable and, after finding the latter together with metric through the field equations, be reconstructed as a consistency condition. The proper solutions may be associated with the scalar-graviton DM. The generally covariant formalism is crucial to this end [9] [10] .

¹⁹A theory of gravity (the so-called “TDiff gravity”) in the generally noncovariant form corresponding here, in this paper, to UR in the gauge was elaborated, irrespective of DM, in [14] .