Journal of Modern Physics
Vol.5 No.8(2014), Article
ID:46359,8
pages
DOI:10.4236/jmp.2014.58070
Numerical Calculations of Some Plasma Parameters of the Capacitively Coupled RF Discharge
Mohamed Ali Hassouba1,2, Ahmed Rida Galaly3,4*, Usama Mohamed Rashed5
1Applied Physics Department, Faculty of Applied Sciences, Taibah University, Medina, KSA
2Physics Department, Faculty of Sciences, Benha University, Qalyubia, Egypt
3Engineering Science Department, Faculty of Community, Umm Al-Qura University, Mecca, KSA
4Physics Department, Faculty of Sciences, Beni-Suef University, Beni-Suef, Egypt
5Physics Department, Faculty of Sciences, Alazhar University, Cairo, Egypt
Email: *ahmed_galaly@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 12 February 2014; revised 11 March 2014; accepted 9 April 2014
ABSTRACT
Numerical calculations by using a self-consistent model of the collisional sheath for the capacitively coupled RF discharge are our target. The results indicated that, at high pressure, the ohmic heating is usually the dominant heating mechanism in the discharge. The power dissipated in the sheath is calculated and compared with the measured data. Moreover, we indicated that, when the gas pressure is increased, the calculated dissipated power is decreased also while the measured input RF power is increased. Furthermore the sheath thickness of the capacitively coupled discharge is calculated and in the same order of the electron oscillation amplitude in the RF field, while the ionization mean free path is shorter than it.
Keywords:RF-Discharge, Self-Consistent Model, Ohmic Heating

1. Introduction
Capacitively coupled RF discharges were widely used in the microelectronics industry for the production of integrated circuits specially processes such as etching and coating [1] -[5] . In these systems, the metallic electrodes were normally enclosed within the reactor and in direct contact with the plasma. External conditions, like pressure, power, geometry and driving frequency determine the properties of the plasma and thus its practical use in various applications [6] .
When RF voltage is applied between two parallel plate electrodes, two sheaths are formed in front of each electrode and plasma connecting these sheaths. These sheaths heat the electrons through a process in which electrons reflected from the moving sheath edge and gained energy on average. This process usually referred to Stochastic heating which is the dominant source of electron heating at low pressure besides the well-known ohmic heating. Heating by RF radiation was very important in the fusion device [7] . Two kinds of electron heating mechanisms may be taken place. Firstly, ohmic heating due to the transfer of energy gained from the acceleration of electrons in electric field to thermal electron energy through collisional processes. Secondly, Stochastic electron heating has been found to be a powerful mechanism in capacitive coupling R-F discharge. Here electrons impinging on the oscillating sheath edge suffer a change of velocity upon reflection back into the bulk plasma. As the sheath moves into the bulk, the reflected ions gain energy, as the sheath moves away, the electron loss energy. However, averaging over an oscillation period, there is a net energy gain.
At sufficiently large RF voltage, the beams of fast electrons ensure the high rate of ionization in the quasineutral plasma. This ionization, as well as the diffusion of charged particles near the boundaries of the sheaths compensates the losses of electrons and ions in the central part of the discharge due to recombination and diffusion. The discharge becomes stable and continues to burn in the strong-current regime, and low-frequency oscillations disappear [8] .
The aim of the present work is using a self-consistent analysis of the collisional sheath of the capacitively coupled RF discharge to calculate the electron ohmic heating power, the average Stochastic power for a single sheath, the power dissipated in the sheath and the sheath thickness and compared the results with the available experimental data.
2. Experimental Setup
The capacitive discharge plasma was formed between two stainless-steel 20 cm diameter electrodes separated by 6 cm. The lower electrode was powered by RF (13.56 MHz), type ENI model OEM-6, generator through a matching box, while the upper electrode as well as the discharge chamber was grounded. The chamber was pumped down by a vacuum system to base pressure of 10−4 torr. During all measurements, continues flow of a gas through the discharge chamber was maintained. High purity Ar gas was used as the working gas and was fed to the chamber through a needle valve. The pressure of the working gas was varied between 1 - 10 torr and measured using a digital vacuum gauge (VAP 5). For displaying the waveform of the discharge current and voltage two channel digital oscilloscope (Tektronix TDS 320, 100 MHz) was used. The applied voltage “V” was measured by using HF voltmeter type B7-37, while the discharge current “I” was measured from its waveform with the help of an oscilloscope. Bird Model 4431-43 Series wattmeter was used to measure the input and/or dissipated powers.
Figure 1 shows a schematic drawing of the apparatus used in this work. Also, Figure 2 shows an example of the waveform of RF discharge at discharge voltage = 950 V and at Ar gas pressure = 1 torr.

Figure 1. It shows a schematic drawing of the experimental setup.

Figure 2. It shows an example of the waveform of RF discharge at discharge voltage = 950 V and at Ar gas pressure = 1 torr.
3. Theoretical Considerations
At high pressure a self-consistent analysis of the collisional sheath is required, which has been given by Liebermann [9] and Godyak [10] . These authors assuming that, the ion mean free path λi is constant independent of the velocity [11] . Also, assuming the ionization occurs in the sheath, and the electrons are accelerated into the plasma.
3.1. Self-Consistent Model
The self-consistent model equations are summarized below. Assuming that the plasma length d » l − 2Sm (where Sm is the maximum sheath thickness) l is the system length, with an initial estimate Sm » 1 cm for numerical computations which is a nominal value for high-pressure capacitive RF discharge. From particle conservations [12] :
 (1)
(1)
(where Kiz is the rate constant for electron-neutral ionization, UB is the Bohm velocity, ng is the neutral atom density and deff is an effective plasma size).
At intermediate and low pressure, we have:
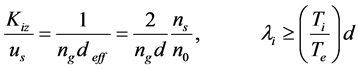 (2)
(2)
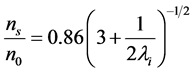 (3)
(3)
(ns is the ion density at the plasma sheath edge, n0 is the plasma density). Where us = uB for collisionless sheath and where at higher pressure one has:
 (4)
(4)
where Kmi is the ion-neutral momentum transfer rate constant.
And the (ns/n0) ratio becomes:
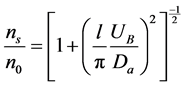 (5)
(5)
where Da is the ambipolar diffusion coefficient. The electron ohmic heating power per unit area is given by:
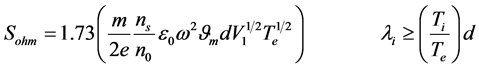 (6)
(6)
 (7)
(7)
where 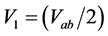 is the fundamental RF voltage amplitude across a single sheath, um is the electron neutral frequency and b is a constant equal to (p/l).
is the fundamental RF voltage amplitude across a single sheath, um is the electron neutral frequency and b is a constant equal to (p/l).
Also, the average Stochastic power for a single sheath is given by:
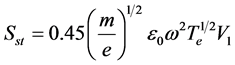 (8)
(8)
The ion kinetic energy per ion hitting the electrode is
![]() (9)
(9)
The electron power balance equation is
 (10)
(10)
So, the total power absorbed per unit area is then found as:
 (11)
(11)
Eliminating ns from Equations (10), (11) and using Equation (9) for V, one can obtain the final equation as:
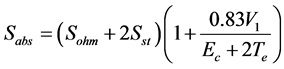 (12)
(12)
Take the following parameters:
p = 1 torr (Ar gas used), l = 10 cmf = 13.56 MHz → ω = 8.6 ´ 107 Hz, VRF = 930 V, Te = 8 eVng = 3.55 ´ 1022 m−3, kiz = 7 ´ 10−15 m3/seckni = 1.4 ´ 10−14 m3/sec and kel = 1.6 ´ 10−13 m3/secStarting with Sm = 1 cm, λi = 3 ´ 10−3 cm, d = l − 2Sm = 8 cm.
\![]() , which is in the high pressure region, in which the plasma is relatively curved in the center. Also, the RF electric field rises at the plates and falls at the mid plane.
, which is in the high pressure region, in which the plasma is relatively curved in the center. Also, the RF electric field rises at the plates and falls at the mid plane.
Substituting into Equations (8), (9) we get:
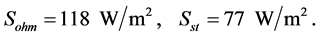
This result indicates that, at high pressure, the ohmic heating is usually the dominant heating mechanism.
3.2. Power Dissipation in the Sheath
The power Ps dissipated in the sheath is given by the product of the time averaged sheath voltage Vp and the ion current IR.
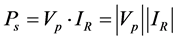 (13)
(13)
After expressing Vp by the Child-Langmuir law:
where
 (14)
(14)
p is the gas pressure in torr, A is the electrode area, k is the ion mobility constant for the used gas and dS is the sheath thickness given by the following equation:
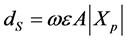 (15)
(15)
where Xp is capacitive reactance of the sheath which given by
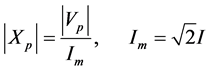 (16)
(16)
where I is discharge current.
After rearrangement the equations one yields;
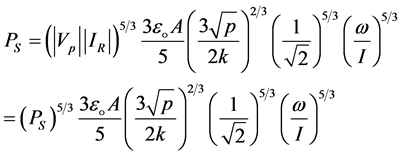 (17)
(17)
After solving for PS, one can obtain the final expression for the power dissipated in the sheath as follows:
 (18)
(18)
3.3. Sheath Thickness
The sheath thickness ds is defined by the capacitor formula Cs = e0A/ds, where Cs is the sheath capacitance.
Relating Cs to X from the relation
![]() (19)
(19)
\ 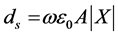 (20)
(20)
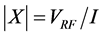 (21)
(21)
where VRF is the RF voltage across the tube and I is the discharge current.
At VRF = 930 V, I = 20 mA and A = 3 ´ 10−2 m−2, then ds is of the order of 0.01 m.
According to the description given by Allen et al. [14] the sheath thickness ds of a capacitively coupled RF discharge should be of the same order of the electron oscillation amplitude Xm in the RF field of the discharge.
\![]() .
.
Those authors give the plausible argument that the maximum distance the electrons can be displaced during a half cycle is equal to the sheath thickness; otherwise they would be captured by the electrodes.
4. Results and Discussion
The relation between the applied voltage “V” and the discharge current “I” of the RF discharge is measured. The measurements have been carried out in the pressure range (0.5 - 2 torr) for Ar gas. I-V characteristic curves for Ar gas at pressures of 0.5, 1, 1.5, and 2 torr are shown in Figure 3.
The relation between the applied voltage and the discharge current can be explained as the following:
When the applied voltage increased the amplitude of the RF electric field is increased, so, the oscillating electrons gain enough energy to make collisions with the neutral particles and increasing the ionization rate, consequently the discharge current would increase. At high pressure, the number of electrons-atom ionizing collision increases, thus, more electrons are produced and consequently, the discharge current is increased. Moreover, the voltage across the plasma sheath cannot be specified independently of the heating mechanism and the power absorbed by the plasma.
On the other hand, the self-consistent model is used for high pressure capacitive RF discharge. Assuming the following: 1) The only loss mechanism is electron loss to the wall; 2) The ionization occurs in the sheath, and the electrons are accelerated into the plasma; 3) The plasma length d » l − 2Sm (where Sm is the maximum sheath thickness) l is the system length, with an initial estimate Sm » 1 cm for numerical computations which is a no-
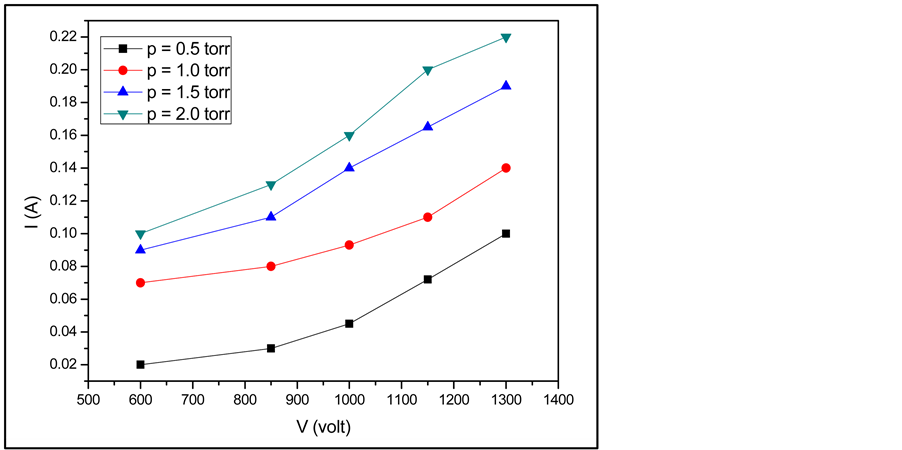
Figure 3. The I-V characteristic curves for Ar gas at different pressures.
minal value for high-pressure capacitive RF discharge.
The electron ohmic heating power per unit area and the average Stochastic power for a single sheath are calculated using Equations (7) and (8) respectively. The calculation results indicate that, at high pressure, the ohmic heating is usually the dominant heating mechanism. Ohmic heating due to the transfer of energy gained from the acceleration of electrons in electric field to thermal electron energy through collisional processes [14] .
The power dissipated in the sheath Ps is calculated using Equation (18), (where the constant k for Ar gas is equal to 103.75 [13] . Figure 4 shows the comparison between the measured dissipated power Ps, measured using the wattmeter, and the calculated one as a function of Ar gas pressure at constant discharge current I = 20 mA. When the gas pressure increased the dissipated power is decreased. At high gas pressure, the secondary electrons traversing the near-electrode sheath have an opportunity to experience one or several elastic and/or inelastic collisions that results in lesser energy acquired by them over the sheath width compared with the case without collisions.
Moreover, Figure 5 shows the relation between the input power of the discharge, which calculated from the measured waveform of the discharge currents, at two constant discharge voltage, as a function of the gas pressure. When the gas pressure increases the gas discharge is more confined in the electrode space due to the lower mean free path associated with a large number of collisions. It’s clear, however, that one can vary the power consumed by the discharge not only by varying the discharge voltage V but also by varying the chamber pressure at a constant V.
In contrast to the measurements presented, the total power measured by the wattmeter, before the matching network, shows the small variations of the order of ±10% when increasing the gas pressure, while the power really consumed in the discharge changes more than that for higher applied voltage. The reason for that is, most of the power output of the power supply is consumed in the matching network and the stray impedance of the system. Thus a relation between the actual dissipated power Ps in the discharge to the total power PT measured by the wattmeter which include, the power consumed in the discharge and the power losses in the matching network, is shown in Figure 6. The actual power is a small non constant fraction of the total power and the amount of power consumed in the discharge is higher at higher applied voltages and gas pressures. This is due to the fact that plasma impedance is changing and thus a large amount of power is transferred from the power supply to the discharge [15] .
Moreover, the sheath thickness ds of a capacitively coupled RF discharge is calculated using Equation (19), ds should be of the same order of the electron oscillation amplitude Xm in the RF field of the discharge. The higher sheath field will increase the amount of power consumed for the acceleration of ions and secondary electrons in the sheath. In the case of higher pressures, the smaller mean free path of the electrons leads to smaller sheath dimensions and thus to higher sheath capacitance [16] .

Figure 4. It shows the comparison between the measured dissipated power Ps, measured using the wattmeter, and the calculated one as a function of Ar gas pressure at constant discharge current I = 20 mA.
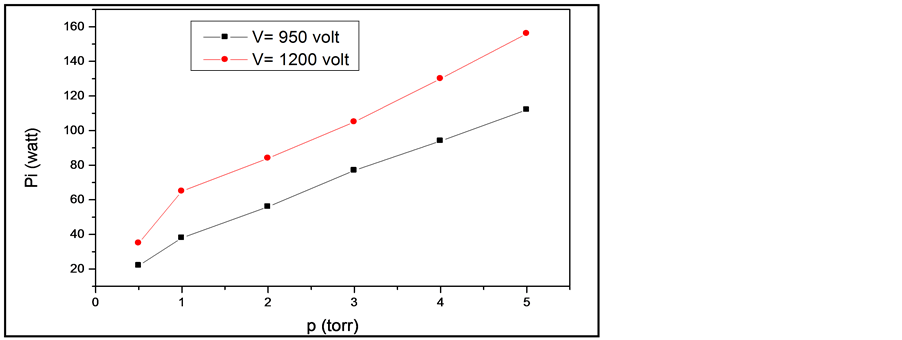
Figure 5. It shows the relation between the input power of the discharge, which calculated from the measured waveform of the discharge currents, at two constant discharge voltage, as a function of the gas pressure.
5. Conclusions
A self-consistent model of the collisional sheath of the capacitively coupled RF discharge at high gas pressure is used. The electron ohmic heating power, the average Stochastic power for a single sheath, the power dissipated in the sheath and the sheath thickness are calculated.
The plasma is produced, using 13.65 MHz RF source, using Ar gas. The relation between the applied voltage “V” and the discharge current “I” of the RF discharge is measured. The voltage across the plasma sheath cannot be specified independently of the heating mechanism and the power absorbed by the plasma. The calculation results indicate that, at high pressure, the ohmic heating is usually the dominant heating mechanism. The electrons are heated by ohmic heating resulting from the volume currents, rather than from sheath heating.
At constant discharge current I = 20 mA, the calculated and/or measured dissipated power in the sheath is decreased when the gas pressure is increased.
The relation between the actual dissipated power Ps in the discharge to the total power PT measured by the wattmeter which include, the power consumed in the discharge and the power losses in the matching network, is
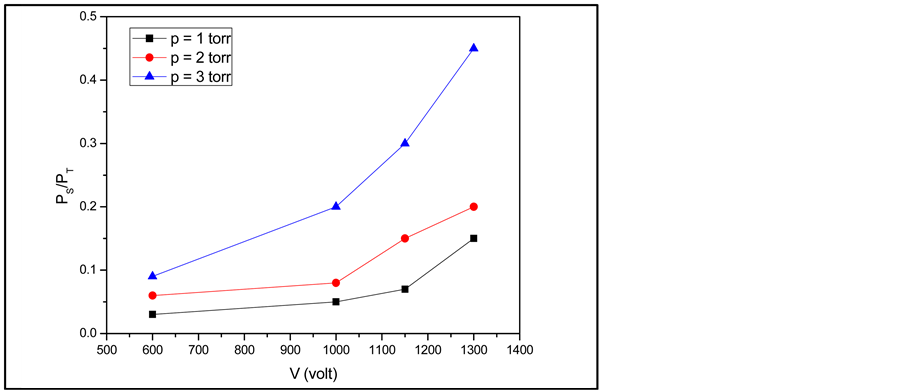
Figure 6. The relation between the ratio (Ps/PT) as a function of the discharge voltage V of the discharge voltage V at different gas pressures
given. The actual power is a small non-constant fraction of the total power and the amount of power consumed in the discharge is higher at higher applied voltages and gas pressures. The power coupling to the discharge is sensitive to the variation of both the discharge voltage and gas pressure.
Moreover, the sheath thickness ds of a capacitively coupled RF discharge is calculated and found to be of the same order of the electron oscillation amplitude Xm in the RF field of the discharge.
References
- Galaly, A.R. and El Akshar, F.F. (2013) International Journal of Multidisciplinary Research and Advances in Engineering (IJMRAE), 5, 169-179.
- Galaly, A.R., Elakshar, F.F. and Khedr, M.A. (2013) Materials Science Forum, 756, 143-150. http://dx.doi.org/10.4028/www.scientific.net/MSF.756.143
- Galaly, A.R. and Elakshar, F.F. (2013) Journal of Modern Physics, 4, 215-225. http://dx.doi.org/10.4236/jmp.2013.42030
- Hassouba, M.A., Nossair, A.M. and El-Akashar, F.F. (2001) Jurnal Fizik Malaysia, 22, 1.
- Lisovskiy, V.A. and Yegorenkov, V.D. (2004) Vacuum, 74, 19-28. http://dx.doi.org/10.1016/j.vacuum.2003.11.003
- Chen, F.F. (2006) Plasma Sources Science and Technology, 15, 773. http://dx.doi.org/10.1088/0963-0252/15/4/022
- Chen, F.F. (2009) Plasma Sources Science and Technology, 18, Article ID: 035012. http://dx.doi.org/10.1088/0963-0252/18/3/035012
- Amanatides, E. and Mataras, D. (2001) Journal of Applied Physics, 89, 1556. http://dx.doi.org/10.1063/1.1337597
- Dudnikov, V. and Dudnikov, A. (2012) Review of Scientific Instruments, 83, Article ID: 02A720.
- Godyak, V.A., Piejak, R.B. and Alexandrovich, B.M. (1991) IEEE Transactions on Plasma Science, 19, 134.
- Liebermann, M.A. (1989) Journal of Applied Physics, 65, 4168. http://dx.doi.org/10.1063/1.343298
- Godyak, V.A. (1990) IEEE Transactions on Plasma Science, 18 159-168. http://dx.doi.org/10.1109/27.45519
- Liebermann, M.A. and Lichtenberg, A.J. (1994) Principles of Plasma Discharges and Materials Processes. John Wiley & Sons Inc., New York.
- Allen, J.A., Boyd, R.L. and Reynolds, P. (1957) Proceedings of the Physical Society B, 70, 297. http://dx.doi.org/10.1088/0370-1301/70/3/303
- Surendra, M. and Graves, D.B. (1990) Applied Physics Letters, 56, 1022. http://dx.doi.org/10.1063/1.102604
- Spiliopoulos, N., Mataras, D. and Rapakoulias, D.E. (1996) Journal of Vacuum Science & Technology A, 14, 2757. http://dx.doi.org/10.1116/1.580197
NOTES
![]()
*Corresponding author.

