Journal of Modern Physics
Vol.5 No.11(2014), Article
ID:47490,9
pages
DOI:10.4236/jmp.2014.511104
Investigation on Virtual State Contribution to Gauge Invariant Cross Section of  in Bethe-Salpeter Framework
in Bethe-Salpeter Framework
Shashank Bhatnagar1, Ming Li2, Shiyuan Li2
1Department of Physics, Addis Ababa University, Addis Ababa, Ethiopia
2School of Physics, Shandong University, Jinan, China
Email: lishy@sdu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2014; revised 12 February 2014; accepted 8 March 2014
ABSTRACT
It is shown that the virtual states and relative momentum of the constituents of the bound states are very important for the cross section of the process  with the help of the Bethe-Salpeter wave function description of the bound states. The gauge invariance of the cross section is demonstrated. The numerical results can explain the experimental data.
with the help of the Bethe-Salpeter wave function description of the bound states. The gauge invariance of the cross section is demonstrated. The numerical results can explain the experimental data.
Keywords:Bethe-Salpeter Wave Function, Virtual States, Relative Momentum

1. Introduction
Heavy quarkonium physics has been the traditional arena of Quantum Chromodynamics (QCD) since 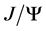 was discovered, in both perturbative (PT) and non-perturbative (NPT) aspects. The heavy quark mass provides a hard scale for PT QCD calculations. The mass term of fermions in the QCD Lagrangian is irrelevant to the colour symmetry, so that the confinement and NPT QCD mechanism for heavy and light quarks could be similar. These facts make the heavy quark a good tool in investigating the unsolved NPT QCD. A simplification is expected from the large mass of the heavy quark, so that it may be non-relativistic (NR) in the bound states. As a matter of fact, not only the relative momentum between heavy quarks in the bound states are considered small, but also these quarks are treated as almost on mass shell. The off shell states and the creation/annihilation of the heavy quarks are not taken into account in the description of the static bound state. This is justified for the rest quarkonia, as investigating their decay widths. In these processes, the largest energy scale is the quarkonium mass
was discovered, in both perturbative (PT) and non-perturbative (NPT) aspects. The heavy quark mass provides a hard scale for PT QCD calculations. The mass term of fermions in the QCD Lagrangian is irrelevant to the colour symmetry, so that the confinement and NPT QCD mechanism for heavy and light quarks could be similar. These facts make the heavy quark a good tool in investigating the unsolved NPT QCD. A simplification is expected from the large mass of the heavy quark, so that it may be non-relativistic (NR) in the bound states. As a matter of fact, not only the relative momentum between heavy quarks in the bound states are considered small, but also these quarks are treated as almost on mass shell. The off shell states and the creation/annihilation of the heavy quarks are not taken into account in the description of the static bound state. This is justified for the rest quarkonia, as investigating their decay widths. In these processes, the largest energy scale is the quarkonium mass![]() . However, in the hard production processes of heavy quarkonium at high energies, the hard scales like the transverse momentum are much larger than
. However, in the hard production processes of heavy quarkonium at high energies, the hard scales like the transverse momentum are much larger than![]() . If there is no well justified factorization formula1 for a certain process, the NR description of the bound states could not be straightforward applicable. In this case, more general framework, which is relativistic and robust to introduce enough number of parameters to describe the bound system, especially the off shell states of the heavy quarks, is needed. The Bethe-Salpeter (BS) wave function framework is one of the good choices. If various relativistic effects are found to be small or could be factorized from the static bound state, the BS framework will naturally leads to the NR descriptions.
. If there is no well justified factorization formula1 for a certain process, the NR description of the bound states could not be straightforward applicable. In this case, more general framework, which is relativistic and robust to introduce enough number of parameters to describe the bound system, especially the off shell states of the heavy quarks, is needed. The Bethe-Salpeter (BS) wave function framework is one of the good choices. If various relativistic effects are found to be small or could be factorized from the static bound state, the BS framework will naturally leads to the NR descriptions.
In this paper, the cross section of the exclusive production process 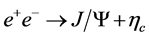 at B factories [1] -[3] is studied in the BS framework. It has been found that the relativistic effects are necessary for explaining the large cross section of this process. We show that both the off-shell heavy quark states as well as the large relative momentum are important in the BS framework.
at B factories [1] -[3] is studied in the BS framework. It has been found that the relativistic effects are necessary for explaining the large cross section of this process. We show that both the off-shell heavy quark states as well as the large relative momentum are important in the BS framework.
The double charm pair production process in B factory energies is of special significance. These four (anti)charms can be respectively grouped into two colour-singlet pairs, hence the colour-octet mechanism never plays important role because of the relatively much smaller colour-octet matrix elements. One can then concentrate on the effects of relative movement and heavy quark off shell states. It has been found that the decay width, as well as the energy distribution of the 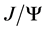 in
in 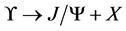 process [4] -[6] can be easily understood by considering such kind of process [7] [8] . It has also been suggested [9] double charm pair production is helpful to analyze the Tevatron polarization ’paradox’, which is refreshed by Tevatron RUNII [10] as well as LHC recently. When the discrepancy between the data [1] -[3] and the lowest order NRQCD calculation [11] -[13] for the exclusive process
process [4] -[6] can be easily understood by considering such kind of process [7] [8] . It has also been suggested [9] double charm pair production is helpful to analyze the Tevatron polarization ’paradox’, which is refreshed by Tevatron RUNII [10] as well as LHC recently. When the discrepancy between the data [1] -[3] and the lowest order NRQCD calculation [11] -[13] for the exclusive process 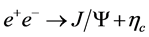 was presented, Many groups recognized and have shown the importance of the relativistic corrections, besides the higher order PT QCD corrections. It has been generally adopted that exclusive process could be more sensitive to the inner movements and more difficult to factorize.
was presented, Many groups recognized and have shown the importance of the relativistic corrections, besides the higher order PT QCD corrections. It has been generally adopted that exclusive process could be more sensitive to the inner movements and more difficult to factorize.
The ways of incorporating the relativistic corrections can be grouped into two: One is in the NRQCD framework, the other is to employ various relativistic wave functions of  and
and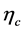 . Works in the NRQCD frameworks [14] [15] show that the relativistic correction is important, at the same time the
. Works in the NRQCD frameworks [14] [15] show that the relativistic correction is important, at the same time the  PQCD corrections are found also very large. The large higher order corrections [16] [17] indicate the requirement of all order summations. For the to-date review of works in this framework, one refers to [18] . Works in the framework of light-cone wave functions [19] -[23] , or other relativistic quark wave function [24] employ the same hard partonic process as the lowest order NRQCD approach. When the scale parameter in the wave function is large, the momentum fraction difference
PQCD corrections are found also very large. The large higher order corrections [16] [17] indicate the requirement of all order summations. For the to-date review of works in this framework, one refers to [18] . Works in the framework of light-cone wave functions [19] -[23] , or other relativistic quark wave function [24] employ the same hard partonic process as the lowest order NRQCD approach. When the scale parameter in the wave function is large, the momentum fraction difference 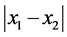 is of
is of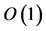 , and this approach can explain the data well. In both the above frameworks, the charm quarks in the bound states are treated as almost on shell, i.e., factorization is assumed.
, and this approach can explain the data well. In both the above frameworks, the charm quarks in the bound states are treated as almost on shell, i.e., factorization is assumed.
On the other hand, the bound states can be described by BS wave functions [25] [26] . The results [25] [26] with the heavy quark limit (HQL) employed and the partonic process the same as that of the lowest order NRQCD approach are consistent with data, i.e., much larger than that of the lowest order NRQCD. However, the HQL generally is considered as to make NR description of the quarks in the bound states valid. This fact implies that different approaches for “NR limit” (HQL vs. NRQCD) could lead to completely different results. There could be effects of the full BS approach not incorporated in the NRQCD framework (but kept in HQL) which enhance the cross section. Such experiences have been seen in history. For the electron in the hydrogen atom, the most important “relativistic effect” comes from the generators of the little group of the Lorentz group (SO(3)), i.e., spin. Such a quantum number can only be naturally deduced from the relativistic wave function/equation of the electron, i.e., the Dirac spinor/equation. The Sommerfeld relativistic corrections to the Bohr theory can never incorporate this.
Of course by the mention of this history we do not imply NRQCD cannot properly incorporate the spin effect of the bound state, but want to point out that it could be better to start from the completely relativistic framework, i.e., the full BS wave function without HQL, to investigate all the relativistic effects in the bound state, namely the off-shell states and the large relative movement of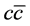 . The off-shell states have never been (and can never) covered in all the above approaches, but once they are taken into account, the Feynman diagrams in Figure 1
. The off-shell states have never been (and can never) covered in all the above approaches, but once they are taken into account, the Feynman diagrams in Figure 1  naturally comes up. These three charm quark lines can never be all on shell at the same time that the four-momenta are all conserved for the two quark-hadron vertices (which requiring at least one of the charm
naturally comes up. These three charm quark lines can never be all on shell at the same time that the four-momenta are all conserved for the two quark-hadron vertices (which requiring at least one of the charm

Figure 1. The momentum of each line is explicitly written.  are colour indices for the quark line. There is another diagram with all the arrows of three loop fermion propagators backward.
are colour indices for the quark line. There is another diagram with all the arrows of three loop fermion propagators backward.
propagators off-shell at the order of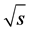 ). Hence all the above mentioned approaches, which neglect the consideration of off-shell states of
). Hence all the above mentioned approaches, which neglect the consideration of off-shell states of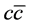 , set these diagrams to be zero by hand. On the contrary, taking into account the the off-shell states and the large relative movement of
, set these diagrams to be zero by hand. On the contrary, taking into account the the off-shell states and the large relative movement of 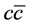 in a self-consistent BS wave function framework, one has to make clear the contribution of these diagrams. Their contribution is not necessarily the leading, but depending on how large the effects of the off-shell states and relative movements, which need the concrete calculations to clarify.
in a self-consistent BS wave function framework, one has to make clear the contribution of these diagrams. Their contribution is not necessarily the leading, but depending on how large the effects of the off-shell states and relative movements, which need the concrete calculations to clarify.
Next section will be the introduction of the BS framework we employ, then followed by Section 3 for describing the calculation details. Here we do the loop integral directly in the momentum space rather than employing the Feynman parameters because of the complex form of the BS vertex. Such a method is quite general and can be applied to the calculation of much more complex production processes in the BS framework. We conclude and discuss at Section 4.
2. The Bethe-Salpeter Framework for the Calculation
In quantum field theory, the BS wave function of a quarkonium is
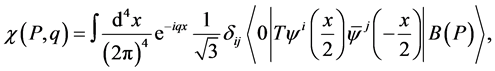 (1)
(1)
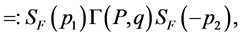 (2)
(2)
where
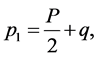
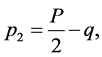 (3)
(3)
for equal mass quark pair. 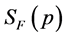 denotes the quark propagator with momentum
denotes the quark propagator with momentum . Equation (2) defines the BS vertex for the coupling of the bound state particle with the composite particles. One simple way to understand this point is that one can get the coordinate space BS wave function
. Equation (2) defines the BS vertex for the coupling of the bound state particle with the composite particles. One simple way to understand this point is that one can get the coordinate space BS wave function 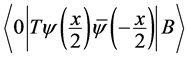 from the Green function
from the Green function 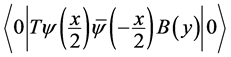 employing the reduction formula. Here
employing the reduction formula. Here 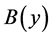 is the field for the bound state particle B. So this
is the field for the bound state particle B. So this 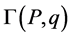 is just the coupling vertex which is the Green function without the external legs. Of course from such an observation we can only obtain the coupling vertex from the BS wave function in the special case that the B particle is on mass shell. However this is enough for our purpose since here we only study the case of the B particle production as the real physical particle. In the following concrete calculations, consistent with all the studies on the decay processes [27] -[29] , we take the quark propagator as the following form with an effective valence quark mass, i.e.,
is just the coupling vertex which is the Green function without the external legs. Of course from such an observation we can only obtain the coupling vertex from the BS wave function in the special case that the B particle is on mass shell. However this is enough for our purpose since here we only study the case of the B particle production as the real physical particle. In the following concrete calculations, consistent with all the studies on the decay processes [27] -[29] , we take the quark propagator as the following form with an effective valence quark mass, i.e.,
 (4)
(4)
For incorporation of the inner information of the bound states obtained from their decay processes which we have investigated in the BS framework [27] -[29] , we here employ the Covariant Instantaneous Ansatz (CIA) for the BS wave function and BS equations same as [27] -[29] (and refs. therein) to do the calculations. In such a framework, the vertex is
 (5)
(5)
where
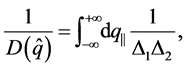 (6)
(6)
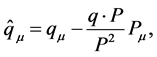 (7)
(7)
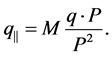 (8)
(8)
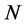 is the normalization factor for the BS wave function.
is the normalization factor for the BS wave function. 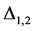 are the form obtained from Equation(4) with the momentum
are the form obtained from Equation(4) with the momentum 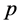 replaced by
replaced by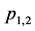 , respectively. Equation (7) shows that the space component of
, respectively. Equation (7) shows that the space component of ![]() is exactly the 3-dimension relative momentum between
is exactly the 3-dimension relative momentum between 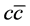 in the quarkonium rest frame.
in the quarkonium rest frame. 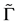 contains the complete Dirac structures. Based on a simple power counting rule which has been investigated to NLO recently [27] -[29] , one can expand the structures as powers of
contains the complete Dirac structures. Based on a simple power counting rule which has been investigated to NLO recently [27] -[29] , one can expand the structures as powers of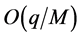 , and fit to the data to get the coefficients order by order. In this work we take the most simple and popular-used structure which belongs to the leading order. For vector meson
, and fit to the data to get the coefficients order by order. In this work we take the most simple and popular-used structure which belongs to the leading order. For vector meson 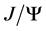
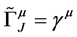 (9)
(9)
For pseudo-scalar meson 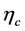
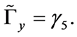 (10)
(10)
From comparing with the decay data, it has been found that the higher order Dirac structures do not contribute significantly to heavy quark bound states [27] -[29] . Only with more and more production processes are investigated within this BS framework and comparing with more and more precise data, it is possible to check how much other Dirac structures contribute in production processes.
The ground state scalar wave function 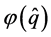 takes the form
takes the form
 (11)
(11)
which leave only one parameter ![]() to be determined. It is clearly defined in [27] -[29] , and is dependent on the quark mass. In this paper we leave it as a free parameter to see the dependence of cross section on it. As can be seen from the scalar wave function,
to be determined. It is clearly defined in [27] -[29] , and is dependent on the quark mass. In this paper we leave it as a free parameter to see the dependence of cross section on it. As can be seen from the scalar wave function, ![]() characterizes the distribution width of the relative momentum between
characterizes the distribution width of the relative momentum between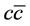 . This point will be further discussed in next section.
. This point will be further discussed in next section.
3. The Calculation Procedure and the Results
The invariant amplitude for the 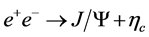 process is
process is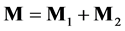 , corresponding to two Feynman diagrams. It is easy to show that
, corresponding to two Feynman diagrams. It is easy to show that , so
, so ![]() is
is
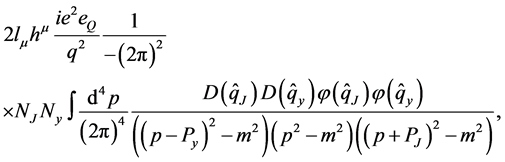 (12)
(12)
with
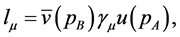 (13)
(13)
and
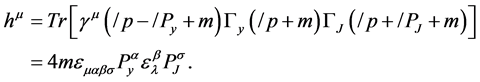 (14)
(14)
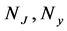 are the normalization factor of
are the normalization factor of 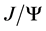 and
and  BS wave functions, respectively. They can be found from [28] [29] , by only keeping the Dirac structures we take into account here. In the above equations,
BS wave functions, respectively. They can be found from [28] [29] , by only keeping the Dirac structures we take into account here. In the above equations, 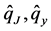 are defined according to Equation (7) w.r.t.
are defined according to Equation (7) w.r.t.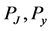 , respectively. According to Equation (3),
, respectively. According to Equation (3),
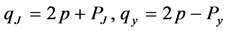 . So all the variables above are functions of
. So all the variables above are functions of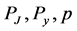 .
.
The electromagnetic (U(1)) gauge invariance for this amplitude is explicit. When replacing the four-vector ![]() by the total four-momentum of the virtual photon,
by the total four-momentum of the virtual photon,  , the above expression (12) is zero. The reason is
, the above expression (12) is zero. The reason is
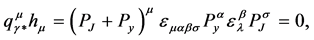 (15)
(15)
because the totally antisymmetric tensor in 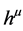 and totally only three independent 4-vectors in the product.
and totally only three independent 4-vectors in the product.
The key point in the calculation is the loop integral in Equation (12). In principle it is simple and straightforward, since there is no divergence so that no regularization and renormalization are needed. However, the complexity of the vertex function makes it difficult to employ the formal and conventional Feynman parameter formulations. it will be more difficult if one want to improve precision by employing a more general form of the vertex (more Dirac structures and more complex form of scalar function) rather than the simplified ones employed in this paper. Here we first integrate over the poles of the propagators and then do the numerical integral for the remaining 3-dimensional momentum. This method, though no help to give analytical results but gives a schematic way to do the calculation to obtain the numerical results for much more complex diagrams. As a matter of fact, one of the purposes for this paper is to explore a systematic and practical way to do calculations for production processes within the BS wave function framework, of which the complexity from the loop integrals is quite common.
Such a method is employed to calculate the high energy scattering amplitude with the help of the flow diagrams, which shows great advantage [30] . The key difference here is that the high energy approximation is not applicable hence not applied. As the consequence, no infrared cutoff caused by the approximation of [30] is needed, so no explicit  dependence (s is the center of mass energy square) is obtained. As another consequence of not applying the high energy limit, there will be more integral regions of the
dependence (s is the center of mass energy square) is obtained. As another consequence of not applying the high energy limit, there will be more integral regions of the  contributing as can be seen in the following.
contributing as can be seen in the following.
We denote the integral in Equation (12) as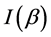 , and write the momenta in light cone coordinates, i.e. for any four momentum
, and write the momenta in light cone coordinates, i.e. for any four momentum 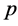

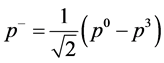
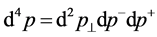 (16)
(16)
Here  and in the concrete calculations we choose the direction of the 3-momentum of
and in the concrete calculations we choose the direction of the 3-momentum of  as the z-axis positive direction. So the integral
as the z-axis positive direction. So the integral  can be written as
can be written as
 (17)
(17)
where
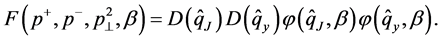 (18)
(18)
We first integrate 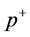 employing the residue theorem. As
employing the residue theorem. As  or
or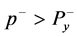 , all poles locate up or under the Real-axis of the complex
, all poles locate up or under the Real-axis of the complex 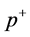 plane, so the integral on
plane, so the integral on 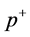 is zero. Therefore, the contributing integral interval of
is zero. Therefore, the contributing integral interval of 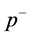 should be
should be  or
or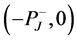 , and
, and 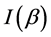 is composed by two parts:
is composed by two parts:
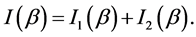 (19)
(19)
Here
 (20)
(20)
with
 (21)
(21)
and
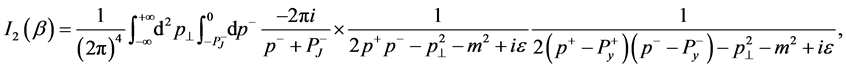 (22)
(22)
with
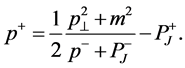 (23)
(23)
The next step is the numerical integral of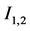 , and the total cross section is straightforward:
, and the total cross section is straightforward:
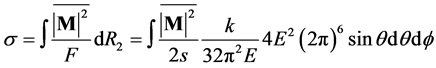 (24)
(24)
 (25)
(25)
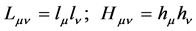 (26)
(26)
The numerical results are listed in Table1
![]() depends on the quark masses and it is around
depends on the quark masses and it is around 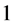 GeV [27] -[29] . Here all the quark masses are taken as half of the bound state masses. Since the masses are almost the same for
GeV [27] -[29] . Here all the quark masses are taken as half of the bound state masses. Since the masses are almost the same for 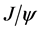 and
and , so we take the same
, so we take the same ![]() for them for simplicity. When taking this
for them for simplicity. When taking this ![]() value, the cross section is not very large but reaches the same order of magnitude as those in the lowest order NRQCD framework [11] -[13] . One can also observe from the table that though the production cross section is quite sensitive to small
value, the cross section is not very large but reaches the same order of magnitude as those in the lowest order NRQCD framework [11] -[13] . One can also observe from the table that though the production cross section is quite sensitive to small ![]() (the cross section should be vanishing for very small
(the cross section should be vanishing for very small![]() , corresponding to the case of the NR limit), it is steady for large
, corresponding to the case of the NR limit), it is steady for large ![]() value. For
value. For ![]() varies from
varies from
1 to 1.9, the cross section varies very slowly. It goes up for larger ![]() value but then decrease for too large (maybe unphysical)
value but then decrease for too large (maybe unphysical) ![]() values. As a matter of fact, the decay constants for
values. As a matter of fact, the decay constants for  and
and 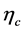 calculated in the BS framework is also not sensitive to the
calculated in the BS framework is also not sensitive to the ![]() value. So one is even possible to take a larger
value. So one is even possible to take a larger ![]() value in calculating the production cross section, say, 2 GeV, to coincide the experimental data at the same time not to change the decay constant much. For this large
value in calculating the production cross section, say, 2 GeV, to coincide the experimental data at the same time not to change the decay constant much. For this large ![]() value, the half width of the energy fraction distribution of a quark in the rest frame of the quarkonium is about 0.3. There is no direct correspondence of this energy fraction to that in the light cone framework, but it is found that to explain the data, the light cone wave function must have a likely wide distribution. Here we will not sharpen the fact that one can explain the data by the lowest order diagrams considered in Figure 1 by taking a large
value, the half width of the energy fraction distribution of a quark in the rest frame of the quarkonium is about 0.3. There is no direct correspondence of this energy fraction to that in the light cone framework, but it is found that to explain the data, the light cone wave function must have a likely wide distribution. Here we will not sharpen the fact that one can explain the data by the lowest order diagrams considered in Figure 1 by taking a large ![]() value, but to emphasize the following points:
value, but to emphasize the following points:
1. In the BS framework, when one takes into account the off shell states and large relative movement of the bound quarks, one can get a large contribution to the production cross section from the diagrams of Figure 1.
2. To get the best value of ![]() so to gain more definite information on the inner movements, it is better to employ more processes to make a global fit. One needs to fit more decay as well as production data. In other words, investigation on various production processes in the BS framework may help to get more precise information for the bound state rather than only consideration on its decay constant.
so to gain more definite information on the inner movements, it is better to employ more processes to make a global fit. One needs to fit more decay as well as production data. In other words, investigation on various production processes in the BS framework may help to get more precise information for the bound state rather than only consideration on its decay constant.
4. Summary and Discussion
The BS wave function framework can naturally take into account the off shell states of 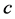 and
and ![]() in the bound states, whose effects are ignored a priori in other frameworks. This framework also naturally takes into account the relative movement of the bound quarks at the same time. Our calculations show that the above effects can contribute significantly to the cross section of the production process
in the bound states, whose effects are ignored a priori in other frameworks. This framework also naturally takes into account the relative movement of the bound quarks at the same time. Our calculations show that the above effects can contribute significantly to the cross section of the production process . One can even get the experimental data by adopting a larger value of
. One can even get the experimental data by adopting a larger value of![]() , i.e., wider relative momentum distribution. The calculations are done with the method of direct integration in the momentum space rather than employing the Feynman parameters. Such a systematic method can be applied to more complex production and decay processes for investigation on the inner information of the bound states within the BS framework.
, i.e., wider relative momentum distribution. The calculations are done with the method of direct integration in the momentum space rather than employing the Feynman parameters. Such a systematic method can be applied to more complex production and decay processes for investigation on the inner information of the bound states within the BS framework.
A question left is how to combine with the calculations in [25] [26] , which could be considered as ‘NNLO’ calculations at HQL of the BS framework. Higher order calculations are straightforward though a little more tedious. But the treating of the propagators and vertices need to be investigated to eliminate double counting. We leave this topic as later works.
There are two papers employing the diagrams like this paper. In [31] it is a hadronic level calculation. Because the quark states (especially when considering the concept of constituent quark) and the hadron states are not orthogonal to each other [32] , it is more interesting to discuss the possible overlap or relation between these two treatments, which could be helpful in clarifying the physical mechanism underlying the QCD bound states. In [33] , the authors employ the QCD sum rule to do the calculations, but it is not clear whether they take into account the off-shell states in their evaluation on the form factors.
Acknowledgements
The authors thank Z.-G. Si for discussion. D. Soper and J.-X. Wang is also thanked for comments on the U(1) gauge invariance. This work is partially supported by NSFC, NSF of Shandong Province with Grant Nos. JQ201101.
References
- Abe, K., et al. (Belle Collaboration) (2002) Physical Review Letters, 89, Article ID: 142001. http://dx.doi.org/10.1103/PhysRevLett.89.142001
- Abe, K., et al. (Belle Collaboration) (2004) Physical Review D, 70, Article ID: 071102. http://dx.doi.org/10.1103/PhysRevD.70.071102
- Aubert, B., et al. (BABAR Collaboration) (2005) Physical Review D, 72, Article ID: 031101. http://dx.doi.org/10.1103/PhysRevD.72.031101
- Bodwin, G.T., Braaten, E. and Lepage, G.P. (1995) Physical Review D, 51, 1125-1171. http://dx.doi.org/10.1103/PhysRevD.51.1125
- Fulton, R., et al. (CLEO Collaboration) (1989) Physics Letters B, 224, 445-449. http://dx.doi.org/10.1016/0370-2693(89)91476-7
- Briere, R.A., et al. (CLEO Collaboration) (2004) Physical Review D, 70, Article ID: 072001. http://dx.doi.org/10.1103/PhysRevD.70.072001
- Li, S.Y., Xie, Q.B. and Wang, Q. (2000) Physics Letters B, 482, 65-70. http://dx.doi.org/10.1016/S0370-2693(00)00439-1
- Han, W. and Li, S.Y. (2006) Physical Review D, 74, Article ID: 117502. http://dx.doi.org/10.1103/PhysRevD.74.117502
- Xie, Q.B. and Li, S.Y. (2000) Contribution of Colour-Singlet Process Upsilon --> J/psi c anti-c g to Upsilon --> J/psi + X, and its indication. Prepared for 3rd Joint Meeting of Chinese Physicists Worldwide: Role of Physics in the New Millenium: Research, Education and Society, Hong Kong, 31 July-4 August 2000, 218-220.
- Abulencia, A., et al. (CDF Collaboration) (2007) Physical Review Letters, 99, Article ID: 132001. http://dx.doi.org/10.1103/PhysRevLett.99.132001
- Braaten, E. and Lee, J. (2003) Physical Review D, 67, Article ID: 054007. http://dx.doi.org/10.1103/PhysRevD.67.054007
- Liu, K.-Y., He, Z.-G. and Chao, K.-T. (2003) Physics Letters B, 557, 45-54. http://dx.doi.org/10.1016/S0370-2693(03)00176-X
- Hagiwara, K., Kou, E. and Qiao, C.-F. (2003) Physics Letters B, 570, 39-45. http://dx.doi.org/10.1016/j.physletb.2003.07.006
- Bodwin, G.T., Lee, J. and Yu, C. (2008) Physical Review D, 77, Article ID: 094018. http://dx.doi.org/10.1103/PhysRevD.77.094018
- He, Z.G., Fan, Y. and Chao, K.T. (2007) Physical Review D, 75, Article ID: 074011. http://dx.doi.org/10.1103/PhysRevD.75.074011
- Gong, B. and Wang, J.X. (2008) Physical Review D, 77, Article ID: 054028. http://dx.doi.org/10.1103/PhysRevD.77.054028
- Zhang, Y.J., Gao, Y.J. and Chao, K.T. (2006) Physical Review Letters, 95, Article ID: 092001. http://dx.doi.org/10.1103/PhysRevLett.96.092001
- Dong, H.R., Feng, F. and Jia, Y. (2012) Physical Review D, 85, Article ID: 114018.http://dx.doi.org/10.1103/PhysRevD.85.114018
- Ma, J.P. and Si, Z.G. (2004) Physical Review D, 70, Article ID: 074007. http://dx.doi.org/10.1103/PhysRevD.70.074007
- Bondar, A.E. and Chernyak, V.L. (2005) Physics Letters B, 615, 215-222. http://dx.doi.org/10.1016/j.physletb.2005.03.021
- Braguta, V.V., Likhoded, A.K. and Luchinsky, A.V. (2005) Physical Review D, 72, Article ID: 074019. http://dx.doi.org/10.1103/PhysRevD.72.074019
- Braguta, V.V., Likhoded, A.K. and Luchinsky, A.V. (2007) Physics Letters B, 646, 80-90. http://dx.doi.org/10.1016/j.physletb.2007.01.014
- Bodwin, G.T., Kang, D. and Lee, J. (2006) Physical Review D, 74, 114028. http://dx.doi.org/10.1103/PhysRevD.74.114028
- Ebert, D., Faustov, R.N., Galkin, V.O. and Martynenko, A.P. (2009) Physics Letters B, 672, 264-269. http://dx.doi.org/10.1016/j.physletb.2009.01.029
- Mengesha, E. and Bhatnagar, S. (2011) International Journal of Modern Physics E, 20, 2521-2533. http://dx.doi.org/10.1142/S0218301311030017
- Guo, X.H., Ke, H.W., Li, X.Q. and Wu, X.H. (2008) Double Heavy-Quarkonium Production from Electron-Positron Annihilation in the Bethe-Salpeter Formalism. arXiv:0804.0949
- Bhatnagar, S. and Li, S.Y. (2006) Decay Constants fp of Unequal-Mass Pseudoscalar Mesons in a Bethe-Salpeter Framework Using a Generalized Structure of Hadron-Quark Vertex Function. arXiv:hep-ph/0612084
- Bhatnagar, S. and Li, S.Y. (2006) Journal of Physics G, 32, 949.
- Bhatnagar, S., Li, S.Y. and Mahecha, J. (2011) International Journal of Modern Physics E, 20, 1437-1454. http://dx.doi.org/10.1142/S0218301311018460
- Cheng, H. and Wu, T.T. (1987) Expanding Prtons: Scattering at High Energies. The MIT Press, Cambridge.
- Zhang, Y.J., Zhao, Q. and Qiao, C.F. (2008) Physical Review D, 78, Article ID: 054014. http://dx.doi.org/10.1103/PhysRevD.78.054014
- Jin, Y., Li, S.Y., Si, Z.G. and Yao, T. (2010) Unitarity and Entropy Change in Exclusive Quark Combination Models. arXiv:1005.4664
- Sun, Y.J., Wu, X.G., Zuo, F. and Huang, T. (2010) The European Physical Journal C, 67, 117-123.http://dx.doi.org/10.1140/epjc/s10052-010-1280-z
NOTES

1Factorization here means that all the effects of the off shell states and creation/annihilation of the heavy quarks, as well as the large relative momentum between them, are well separated into the hard part which is calculable via PT QCD, so that the bound state can be described by NR effective theories, such as .


