Journal of Modern Physics
Vol.5 No.5(2014), Article ID:44249,12 pages DOI:10.4236/jmp.2014.55029
Rayleigh-Taylor Instability of Magnetized Plasma through Darcy Porous Medium
Gamal Abdallah Hoshoudy
Department of Applied Mathematics and Computer Science, Faculty of Science, South Valley University, Kena, Egypt
Email: g_hoshoudy@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 December 2013; revised 25 January 2014; accepted 23 February 2014
ABSTRACT
Effects of horizontal and vertical magnetic field components on the Rayleigh-Taylor instability of stratified incompressible plasmas layer of variable density through Darcy porous medium are studied. The basic magnetohydrodynamic (MHD) set of equations has been constructed and linearized. Then the linear normalized growth rate is obtained analytically as a function of the physical parameters of the system considered. Numerical calculations have been performed to see the effects of various parameters on the normalized growth rate of Rayleigh-Taylor instability. It is found that the parameter 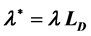 (
( is constant and
is constant and  is the density-scale length) has an important role on the happening stability, where the maximum instability comes at
is the density-scale length) has an important role on the happening stability, where the maximum instability comes at  and to get more stable model we select
and to get more stable model we select  through the region
through the region . The system will be more stable for the positive values of
. The system will be more stable for the positive values of .
.
Keywords:Rayleigh-Taylor Instability; Magnetized Plasmas; Darcy Porous Media

1. Introduction
The hydromagnetics stability of a magnetized plasma of varying density is of considerable importance in several astrophysical situations such as supernova explosions, in heating in solar corona, theories of sunspot magnetic fields, the formation and mixing of clouds and the stability of the stellar atmospheres in magnetic fields.
The classical study of the equilibrium of an incompressible, inviscid fluid of variable density was first undertaken by Rayleigh [1] , and later applied to all accelerated fluids by Taylor [2] . Rayleigh showed the equilibrium of a horizontal layer of incompressible, ideal fluid is stable or unstable according as the density increases or decreases anywhere in the vertically upward direction. Since then the problem is called Rayleigh-Taylor instability (RTI). RTI occurs naturally in many phenomenons of astrophysics, geophysics, and laboratories. It derives its character from the adverse density distribution of the matter, where the investigation of Rayleigh-Taylor instabilities in a magnetized plasma is a problem of considerable interest in space (ionospheric spread-F), fusion (curvature induced instabilities like interchange, ballooning, etc.) and the astrophysical plasmas.
Under various physical effects, the Rayleigh-Taylor instability problem of a finite layer of a fluid has been studied by several authors in hydrodynamics and in magnetohydrodynamics domain; the stabilizing effect of magnetic field on RTI problem for an incompressible plasma has been demonstrated by Kruskal and Schwarzschild [3] for a horizontal orientation of the magnetic field and by Hide [4] for a vertical orientation. The effects of viscosity and compressibility on the RTI of stratified plasma in the presence of magnetic field have been studied by Bhatia [5] . The RTI in a rotating plasma of variable density including simultaneously the effects of viscosity and the finiteness of the ion Larmor radius have been investigated by Bhatia and Steiner [6] . The effect of Hall current and finite electrical resistivity on the RTI of viscous, incompressible, finitely conducting plasma in a downward gravitational field under the influence of a uniform magnetic field normal to gravity has been studied by Kamla and Srivastav [7] . The RTI of an infinitely conducting stratified dusty plasma medium including the effects of FLR corrections in the presence of a horizontal magnetic field has been studied by Kamal and Chhajlani [8] . The RTI of a plasma layer in the presence of a horizontal magnetic field is investigated, taking into account the effects of Hall-currents and an arbitrarily large density gradient by Donald [9] . The effects of Hall currents and viscosity on the RTI of an incompressible infinitely conducting stratified plasma permeated by a two-dimensional horizontal magnetic field have been investigated by Ahsan and Bhatia [10] . The effects of Hall currents on the RTI of a finitely conducting stratified partially ionized plasma, where the plasma is permeated by a two dimensional horizontal magnetic field have been studied by Aiyub and Bhatia [11] . In the presence of magnitude of the gravitational acceleration, the RTI of stratified incompressible plasma has been studied by Goldston and Rutherford [12] . The RTI in the presence of horizontal magnetic field of incompressible plasma has been studied by Wu et al. [13] .
The RTI of magnetized plasma through porous medium problem has a great scientific interest, where this problem corresponds physically (in astrophysics) to the Rayleigh-Taylor instability of an equatorial section of a planetary magnetosphere or of a stellar atmosphere where the magnetic field is perpendicular or parallels to gravity. So, the RTI of a stratified plasma through porous medium in the presence or absence of magnetic field has been studied by a number of researchers (Chhajlani and Vaghela, Vyas and Chhajlani, Sharma and Bhardwaj, Sharma and Sharma, Sharma and Trilok, Sharma and Sunil, Shikha and Bhatia, Opara, Sharma and Sunil, Sunil and Sharma, Sharma and Thakur and Sharma and Rajput). In this case (Darcy’s model), the usual viscous term in the equation of motion is replaced by the resistive term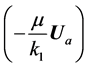 , where
, where  is the fluid viscosity,
is the fluid viscosity,  is the medium permeability and
is the medium permeability and  is the Darcian (filter) velocity of the fluid.
is the Darcian (filter) velocity of the fluid.
In all the above-mentioned studies, the behaviour of growth rates is considered with respect to the porosity of porous medium and the medium permeability in the presence of an variable magnetic field in  direction only or in
direction only or in 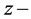 direction only. Here, we will discuss the role of resistive term (Darcy’s term) besides the components of magnetic field in both
direction only. Here, we will discuss the role of resistive term (Darcy’s term) besides the components of magnetic field in both 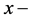 and
and 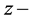 direction on growth rates of RTI of plasma layer
direction on growth rates of RTI of plasma layer
2. Formulation of the Problem
We consider the strata of incompressible and inviscous plasma as a fluid of electrons and immobile ions through Darcy porous medium in the presence of magnetic field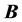 , where the relevant equations may be written, respectively (see references [12] -[25] ),
, where the relevant equations may be written, respectively (see references [12] -[25] ),
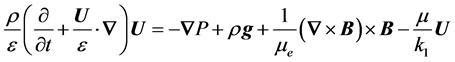 , (1)
, (1)
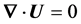 , (2)
, (2)
 . (3)
. (3)
For incompressible flow the fluid elements move without changing density is to say that the Lagrangian total derivative of density is zero, that is (see reference [1] )
 (4)
(4)
where 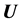 is the velocity of the fluid,
is the velocity of the fluid,  is the density,
is the density,  thermal pressure,
thermal pressure, 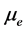 magnetic permeability,
magnetic permeability,  coefficient of dynamic viscosity and
coefficient of dynamic viscosity and 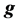 is the gravitational acceleration.
is the gravitational acceleration.
One can see that the set of Equations (1)-(4) is complete for describing the magnetic field effects on the R-T instability of incompressible plasma, since its number of equations exactly equals its number of unknown quantities: Two unknown vector quantities 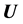 and
and 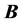 and two unknown scalar quantities
and two unknown scalar quantities  and
and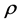 . For the equilibrium profiles can be expressed in the form
. For the equilibrium profiles can be expressed in the form 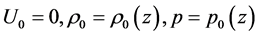 and
and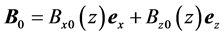 .
.
Now, we assume a small perturbation in the system of Equations (1)-(4), where the perturbations in the velocity , pressure
, pressure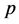 , magnetic field
, magnetic field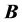 , and density
, and density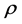 , respectively, are
, respectively, are 
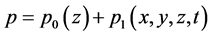 ,
, 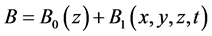 , and
, and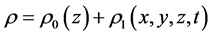 . Then, the linearized equations can be easily derived from Equations (1)-(4) in the form
. Then, the linearized equations can be easily derived from Equations (1)-(4) in the form
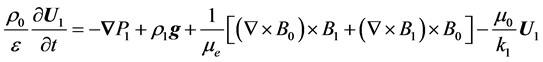 (5)
(5)
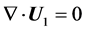 (6)
(6)
 (7)
(7)
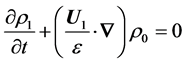 (8)
(8)
Now, let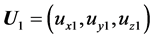 ,
, 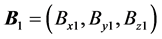 ,
, 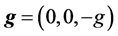 and the fluid is arranged in horizontal strata, then
and the fluid is arranged in horizontal strata, then 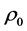 is a function of the vertical coordinate
is a function of the vertical coordinate 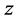 only (i.e.
only (i.e. ) and
) and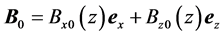 . Then the system of Equations (4)-(8) become
. Then the system of Equations (4)-(8) become
 (9)
(9)
 (10)
(10)
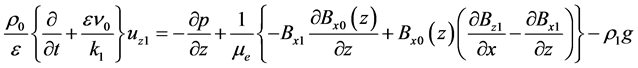 (11)
(11)
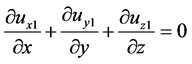 (12)
(12)
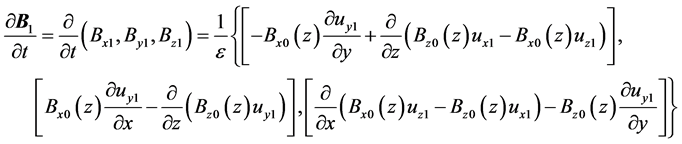 , (13)
, (13)
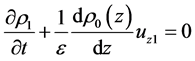 (14)
(14)
If we assume that the perturbation in any physical quantity takes the form
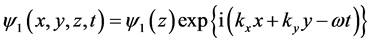 , (15)
, (15)
where 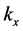 and
and 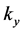 are horizontal components of the wave-number vector
are horizontal components of the wave-number vector  such that
such that 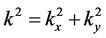 and
and 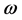 (may be complex
(may be complex ) is the frequency of perturbations or the rate at which the system departs from equilibrium thee initial state. Using the expression (15) in the system of Equations (9)-(14), we have
) is the frequency of perturbations or the rate at which the system departs from equilibrium thee initial state. Using the expression (15) in the system of Equations (9)-(14), we have
 , (16)
, (16)
 , (17)
, (17)
 , (18)
, (18)
 , (19)
, (19)
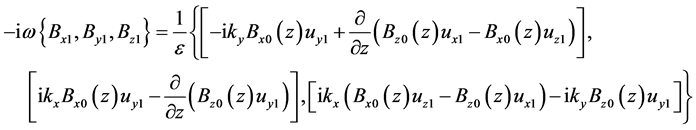 , (20)
, (20)
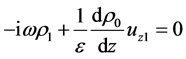 , (21)
, (21)
Now, if we eliminate some of the variables from the system of Equations (16)-(21), we have a differential equation in 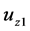
 , (22)
, (22)
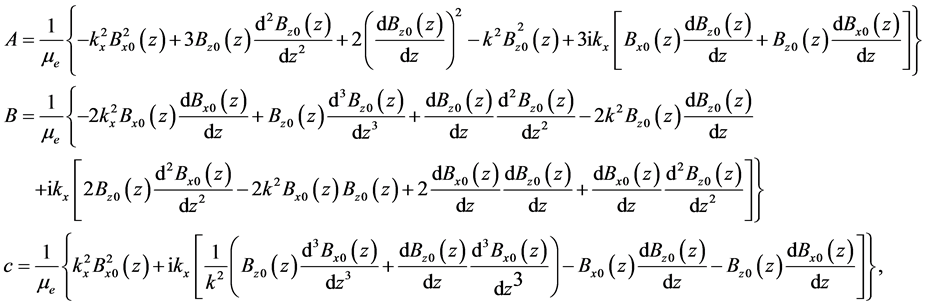
(23)
3. A Continuously Stratified Plasma
In this section we consider the case of incompressible continuously stratified plasma layer of thickness  confined between two rigid boundaries, in which the density and magnetic field distribution are given, respectively, by
confined between two rigid boundaries, in which the density and magnetic field distribution are given, respectively, by
 ,
, 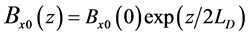 and
and 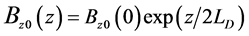
where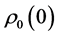 ,
,  and
and 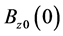 and
and 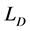 (the density-scale length) are constants, then Equation (22) takes the form
(the density-scale length) are constants, then Equation (22) takes the form
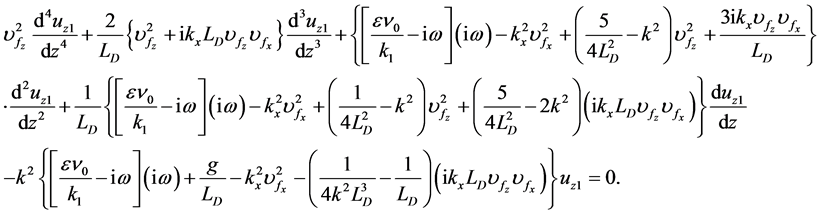 (24)
(24)
where 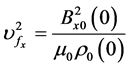 and
and  are Alfvén velocity.
are Alfvén velocity.
Now, if we choose 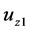 in the form
in the form 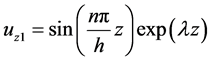 and by substituting in Equation (24), we will have an equation in both
and by substituting in Equation (24), we will have an equation in both  and
and . Then coefficients both
. Then coefficients both 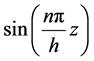 and
and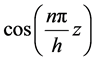 , respectively, are given by:
, respectively, are given by:
 (25)
(25)
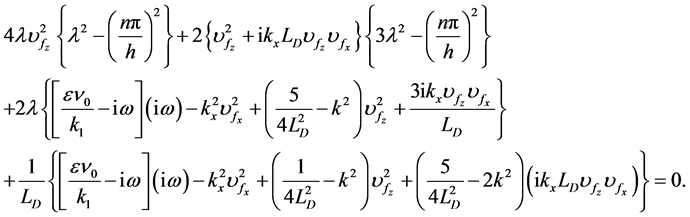 (26)
(26)
Now, we define the dimensionless quantities
 (27)
(27)
Then Equations (25) and (26), respectively, take the form
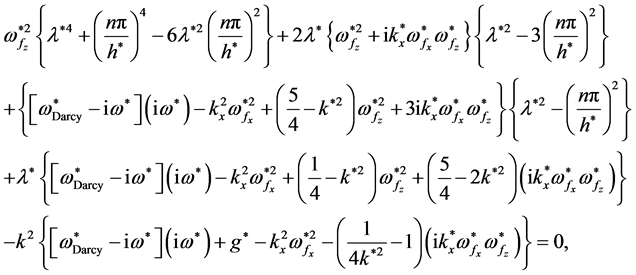 (28)
(28)
 (29)
(29)
Now, we put  and for
and for  (stable oscillations), then Equations (28) and (29) may be given by:
(stable oscillations), then Equations (28) and (29) may be given by:
 (30)
(30)
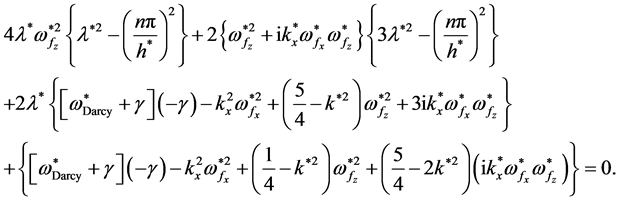 (31)
(31)
Now, if we rearrange the above two equations (Equations (30) and (31)), we will have
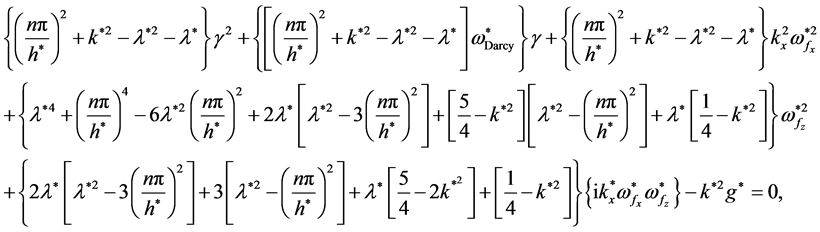 (32)
(32)
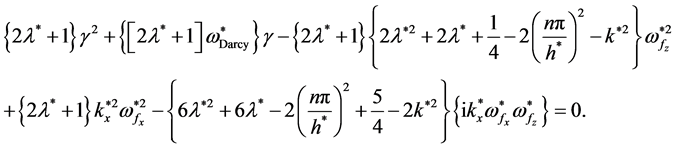 (33)
(33)
From Equations (32) and (33) maybe we can specialize the next special cases:
(i) In the case of 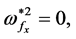
 and
and 
From Equation (33) we get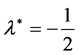 , and substituting in Equation (32) we find that the normalized growth rate given by
, and substituting in Equation (32) we find that the normalized growth rate given by
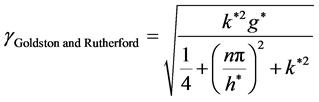 (34)
(34)
This case is considered by Goldston and Rutherford (see reference [12] ).
(ii) In the case of 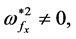
 and
and 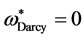
A second time, from Equation (33) we get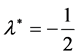 , and substituting in Equation (32), then the normalized growth rate given by
, and substituting in Equation (32), then the normalized growth rate given by
 . (35)
. (35)
This case studied in reference [12] . It is clarified that, the horizontal magnetic field has stabilizing effect on RTI problem. This influence is obvious from Equations (34) and (35), where 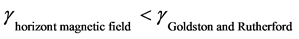 .
.
(iii) In the case of 
 and
and 
A third time, from Equation (33) we get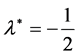 , and substituting in Equation (32), the normalized growth rate given by
, and substituting in Equation (32), the normalized growth rate given by
 . (36)
. (36)
Now, comparing between Equations (34) and (36), someone can observe that, the stabilizing role for the vertical magnetic field on the considerable system, where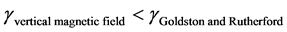 .
.
(iv) In the case of 
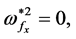 and
and 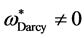
A fourth time, from Equation (33) we get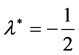 , and substituting in Equation (32), the dispersion rate given by
, and substituting in Equation (32), the dispersion rate given by
 (37)
(37)
Then, the normalized growth rate becomes
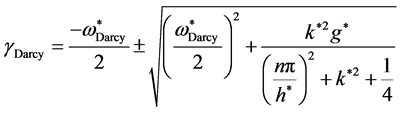 . (38)
. (38)
From Equations (34) and (38) it is very clear that, .
.
The stabilizing effects of the horizontal, vertical magnetic and resistive term, unaccompanied, (above cases (i)-(iv)) on the RTI have been numerically presented in Figure 1.
(v) For the general case (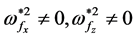 and
and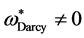 ), if we eliminate the term
), if we eliminate the term  between Equations (32) and (33) the normalized dispersion relation takes in the form.
between Equations (32) and (33) the normalized dispersion relation takes in the form.
 (39)
(39)
In this case the normalized growth rate given as.
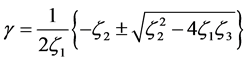 (40)
(40)
where
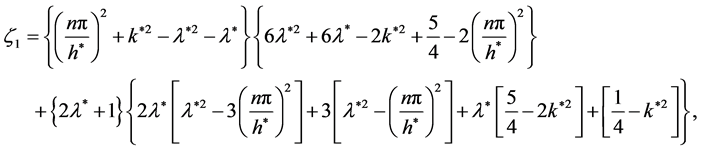 (41)
(41)
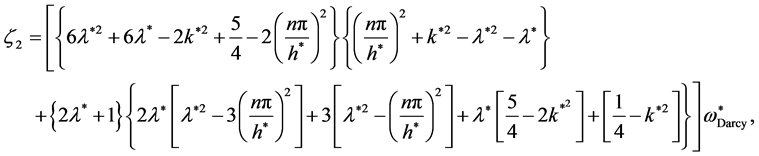 (42)
(42)

Figure 1. The role of parameter’s problem, unaccompanied, where the square normalized growth rate 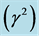 against the square normalized wave number
against the square normalized wave number 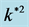 is plotted at
is plotted at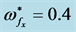 ,
, 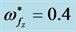 and
and .
.
 (43)
(43)
In fact, the square of normalized growth rate  in Equation (40) is a function in the dimensionless quantities of horizontal
in Equation (40) is a function in the dimensionless quantities of horizontal 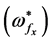 and vertical
and vertical  components of the magnetic field, the dimensionless resistive term
components of the magnetic field, the dimensionless resistive term , dimensionless Darcy term
, dimensionless Darcy term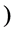 , the wave number
, the wave number  and
and  (
( , where
, where 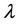 is constant and
is constant and 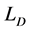 is the density-scale length). The dimensionless quantities
is the density-scale length). The dimensionless quantities ,
,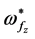 and
and  are the parameters of problem that maybe take a different values. But the constant
are the parameters of problem that maybe take a different values. But the constant 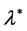 is unknown in the general case (v), while in the absence of magnetic field or in the presence of either them (horizontal or vertical magnetic field components) we note that
is unknown in the general case (v), while in the absence of magnetic field or in the presence of either them (horizontal or vertical magnetic field components) we note that  (special cases (i)-(iv)). So, firstly we will discuss the role of constant
(special cases (i)-(iv)). So, firstly we will discuss the role of constant 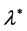 on the square of normalized growth rate
on the square of normalized growth rate 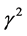 in the presence of horizontal, vertical magnetic field components and resistive term.
in the presence of horizontal, vertical magnetic field components and resistive term.
The role of constant 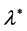 in the presence of both horizontal and vertical magnetic field components
in the presence of both horizontal and vertical magnetic field components
 and resistive term
and resistive term  is plotted in Figure 2, where the square normalized growth
is plotted in Figure 2, where the square normalized growth
Figure 2. The role of constant 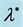 on the
on the  in the presence of
in the presence of  and the resistive term
and the resistive term  through the range
through the range .
.
rate  is plotted against
is plotted against 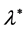
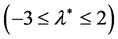 at
at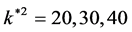 . For the values
. For the values  that is less than
that is less than , one can see that, the magnitude of
, one can see that, the magnitude of 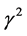 decrease with decreasing of
decrease with decreasing of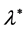 . For the values
. For the values 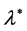
that is greater than  the magnitude of
the magnitude of  decrease while the magnitude of
decrease while the magnitude of 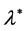 increases. These implies that the maximum instability in the presence of both horizontal and vertical components of magnetic field happens at
increases. These implies that the maximum instability in the presence of both horizontal and vertical components of magnetic field happens at 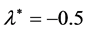 (in the presence or absence of resistive term).
(in the presence or absence of resistive term).
The general case (Equation (40)), that gives the effects of horizontal, vertical magnetic field and resistive term together on the instability of the considered system has been presented in Figure 3. where the square normalized growth rate  is plotted against the square normalized wave number
is plotted against the square normalized wave number 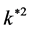 at
at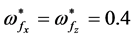 ,
, 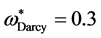 and for different values of
and for different values of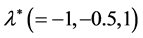 . Second time, one can see that, the maximum instability (maximum square normalized growth rate
. Second time, one can see that, the maximum instability (maximum square normalized growth rate ) happens at
) happens at  and at
and at 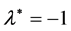 the magnitudes of
the magnitudes of  are less than their counterpart at
are less than their counterpart at . Also, the magnitudes of
. Also, the magnitudes of  at
at  are less than their counterpart at
are less than their counterpart at . Moreover the magnitudes of
. Moreover the magnitudes of 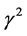 at
at 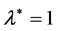 are less than their counterpart at
are less than their counterpart at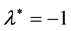 .
.
In the case  (maximum instability) the system of Equations (39)-(43) take the form:
(maximum instability) the system of Equations (39)-(43) take the form:
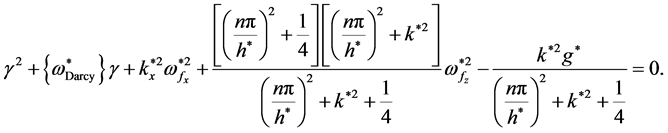 (44)
(44)
Then the maximum normalized growth rate gives by
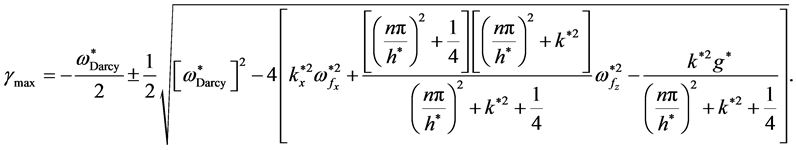 (45)
(45)
Finally, Figure 4 Shows the role of constant , where the maximum happens at
, where the maximum happens at . If we move
. If we move

Figure 3. The square normalized growth rate  against the square normalized wave number
against the square normalized wave number  in the presence of
in the presence of  and the resistive term
and the resistive term .
.
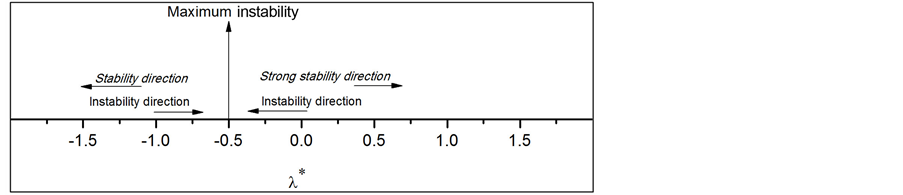
Figure 4. Sketch of the 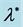 through the range
through the range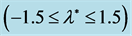 .
.
toward the point 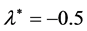 from the right or left hand the system moves toward instability and vice versa if we move from the point
from the right or left hand the system moves toward instability and vice versa if we move from the point 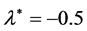 to the left or right hand, the system tends to stability.
to the left or right hand, the system tends to stability.
In closing this paper, the Rayleigh-Taylor instability in stratified plasma in the presence of combined effect of horizontal and vertical magnetic field through Darcy porous medium is considered. The solution of the system leads to a dispersion relation where the physical parameters are put in the dimensionless form. Some special cases are particularized to explain the roles that play the variables of the problem and numerical solutions are made. Some stability diagrams are plotted and discussed. The results show that, as the growth rate depends on the horizontal and vertical components of magnetic field and resistive term (Darcy’s term) also depends on the parameter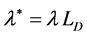 . Numerically the maximum instability (normalized growth rate) happens at
. Numerically the maximum instability (normalized growth rate) happens at  and then analytically the maximum instability gives in Equation (45). The system will be more stable if we select
and then analytically the maximum instability gives in Equation (45). The system will be more stable if we select  such that to be different than −0.5. Finally, for the behavior of our selected system with respect to the parameter
such that to be different than −0.5. Finally, for the behavior of our selected system with respect to the parameter 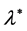 we have not clear interpreting at this stage.
we have not clear interpreting at this stage.
References
References
Rayleigh, L. (1882) Proceedings of the London Mathematical Society, 14, 170-177. http://dx.doi.org/10.1112/plms/s1-14.1.170
Taylor, G.I. (1950) Proceeding of the Royal Society of London Series A, 201, 192-196. http://dx.doi.org/10.1098/rspa.1950.0052
Kruskal M. and Schwarzschild, M. (1954) Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 223, 348-360. http://dx.doi.org/10.1098/rspa.1954.0120
Hide R. (1955) Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 233, 376- 396. http://dx.doi.org/10.1098/rspa.1955.0273
Bhatia, P.K. (1974) Astrophysics and Space Science, 26, 319-325. http://dx.doi.org/10.1007/BF00645614
Bhatia P.K. and Steiner, J.M. (1975) Astrophysics and Space Science, 34, 459-465. http://dx.doi.org/10.1007/BF00644812
Abani K. and Srivastav, K.M. (1975) Il Nuovo Cimento B Series 11, 26, 419-432. http://dx.doi.org/10.1007/BF02738570
Sanghvi, R.K. and Chhajlani, R.K. (1987) Astrophysics and Space Science, 132, 57-64. http://dx.doi.org/10.1007/BF00637781
Donald Ariel, P. (1991) Astrophysics and Space Science, 184, 205-219. http://dx.doi.org/10.1007/BF00642969
Ali A. and Bhatia, P.K. (1993) Physica Scripta, 47, 567-570. http://dx.doi.org/10.1088/0031-8949/47/4/016
Khan A. and Bhatia, P.K. (1993) Physica Scripta, 48, 607-611. http://dx.doi.org/10.1088/0031-8949/48/5/017
Goldston R.J. and Rutherford, P.H. (1995) Introduction to Plasma Physics Institute of Physics, Institute of Physics Publishing, Bristol. http://dx.doi.org/10.1201/9781439822074
Wu, Z. Zhang, W., Li, D. and Yang, W. (2004) Chinese Physics Letters, 21, 2001-2004. http://dx.doi.org/10.1088/0256-307X/21/10/038
Vyas, M.K. and Chhajlani, R.K. (1988) Astrophysics and Space Science, 140, 89-104. http://dx.doi.org/10.1007/BF00643533
Sharma, R.C. and Bhardwaj, V.K. (1990) Czechoslovak Journal of Physics, 40, 753-760. http://dx.doi.org/10.1007/BF01606015
Sharma, R.C. and Sharma, Y.D. (1989) Astrophysics and Space Science, 155, 295-300. http://dx.doi.org/10.1007/BF00643865
Sharma, R.C. and Chand, T. (1989) Astrophysics and Space Science, 155, 301-310.
Sharma, R.C. and Sunil (1992) Astrophysics and Space Science, 194, 303-311. http://dx.doi.org/10.1007/BF00643999
Oza, S. and Bhatia, P.K. (1993) Astrophysics and Space Science, 199, 279-288. http://dx.doi.org/10.1007/BF00613201
Opara, F.E. (1994) Astrophysics and Space Science, 213, 197-204. http://dx.doi.org/10.1007/BF00658210
Sharma, R.C. and Sunil (1994) Czechoslovak Journal of Physics, 44, 927-936. http://dx.doi.org/10.1007/BF01715486
Sharma, R.C. and Sunil (1995) Physics of Plasmas, 2, 1886-1892. http://dx.doi.org/10.1063/1.871275
Sunil and Sharma, Y.D. (1996) Polymer-Plastics Technology and Engineering, 35, 221-231. http://dx.doi.org/10.1080/03602559608000580
Sharma, R.C. and Thakur, K.P. (1982) International Journal of Mathematics and Mathematical Sciences, 5, 365-367. http://dx.doi.org/10.1155/S0161171282000350
Sharma, R.C. and Rajput, A. (1992) Astrophysics and Space Science, 187, 105-111. http://dx.doi.org/10.1007/BF00642690

