Journal of Modern Physics
Vol.5 No.7(2014), Article ID:45449,9 pages DOI:10.4236/jmp.2014.57064
Spin-Magnetic Moment of Dirac Electron, and Role of Zitterbewegung
Shigeru Sasabe
Department of Science & Technology, Tokyo Metropolitan University, Tokyo, Japan
Email: s-sasabe@tmu.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 20 December 2013; revised 18 January 2014; accepted 15 February 2014
ABSTRACT
The spin-magnetic moment of the electron is revisited. In the form of the relativistic quantum mechanics, we calculate the magnetic moment of Dirac electron with no orbital angular-momentum. It is inferred that obtained magnetic moment may be the spin-magnetic moment, because it is never due to orbital motion. A transition current flowing from a positive energy state to a negative energy state in Dirac Sea is found. Application to the band structure of semiconductor is suggested.
Keywords:Spin-Magnetic Moment, Zitterbewegung, G-Factor, Dirac Electron, Band Structure, Semiconductor

1. Introduction
The spin and the spin-magnetic moment are basic and the most important concepts in the spintronics [1] that is new research field in considerable expansion. In the previous work [2] , we found that the spin-magnetic moment seems to be caused from well-known definitional equation of magnetic moment. Such a case never happen in the non-relativistic quantum mechanics. In the relativistic quantum mechanics, however, the electron has another degree of freedom called Zitterbewegung [3] -[5] that is trembling motion of relativistic electron. Some physical connection between the spin-magnetic moment and Zitterbewegung was implied in the previous work [2] .
In this paper, we investigate a question about the origin of the spin-magnetic moment of the electron and roles of Zitterbewegung relating to it. The use of Heisenberg picture will make hidden roles of Zitterbewegung more clear than previous work. On the other hand, Zitterbewegung in solid state physics [6] -[8] has been a subject of great interest in recent years, since observable Zitterbewegung-like dynamics of band electron was predicted [9] [10] for electron moving in narrow-gap semiconductors [11] , graphene sheets [12] , carbon nanotube [13] , and super conductor [14] . Our research in this paper is therefore worthwhile on both sides of science and technology. As a result, we obtain
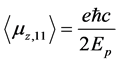 (1)
(1)
more easily than the previous work [2] , where 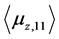 denotes expectation value of z-component of spin-magnetic moment of a free Dirac electron in positive energy state.
denotes expectation value of z-component of spin-magnetic moment of a free Dirac electron in positive energy state.
2. Relation between Spin and Spin-Magnetic Moment
It is well known that the relativistic electron put in the external magnetic field gives interaction energy with the magnetic field . This term [15] [16]
. This term [15] [16]
 (2)
(2)
was understood as the interaction energy  between an external magnetic field
between an external magnetic field  and the magnetic moment
and the magnetic moment![]() . Then, physicists concluded that
. Then, physicists concluded that
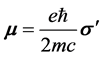 (3)
(3)
must be the spin-magnetic moment of the electron in comparison with Equation (2). However, Equation (3) provided merely the relation of the spin-magnetic moment ![]() and the spin operator
and the spin operator  by the analogy with classical electrodynamics. We do not still know how the spin-magnetic moment is generated, and what the spin-magnetic moment is. In order to clarify the origin of the spin-magnetic moment, we must deduce it without the external magnetic field which always leads to the interaction energy of the form
by the analogy with classical electrodynamics. We do not still know how the spin-magnetic moment is generated, and what the spin-magnetic moment is. In order to clarify the origin of the spin-magnetic moment, we must deduce it without the external magnetic field which always leads to the interaction energy of the form . Generally, the magnetic moment for a charged particle moving with the velocity
. Generally, the magnetic moment for a charged particle moving with the velocity  and the charge
and the charge 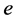 is defined as [17] [18]
is defined as [17] [18]
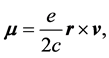 (4)
(4)
in the classical electrodynamics, where 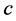 is speed of light. In the non-relativistic quantum theory, the above equation can be expressed as
is speed of light. In the non-relativistic quantum theory, the above equation can be expressed as
 (5)
(5)
by using  and
and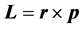 .
.
In relativistic quantum theory, however, we should mind that we can not use Equation (5) for Dirac electron, because the velocity 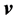 and the momentum
and the momentum ![]() are independent variables to each other (i.e.
are independent variables to each other (i.e.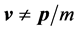 ) in this case [2] .
) in this case [2] .
3. Zitterbewegung
As to Zitterbewegung, we briefly show all equations that are needed later. The velocity 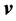 of Dirac electron is given [19] by Heisenberg equation,
of Dirac electron is given [19] by Heisenberg equation,
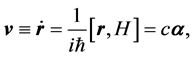 (6)
(6)
where 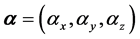 are the Dirac matrices in Dirac Hamiltonian
are the Dirac matrices in Dirac Hamiltonian
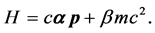 (7)
(7)
The 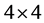 matrices
matrices ![]() and
and 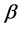 are defined as
are defined as
 (8)
(8)
where  are the Pauli matrices. These matrices satisfy the following relations:
are the Pauli matrices. These matrices satisfy the following relations:
 (9)
(9)
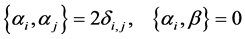 (10)
(10)
In order to clarify the role of Zitterbewegung, we use Heisenberg picture hereafter to calculate the time evolution of any operator. We first investigate the behavior of matrix 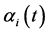 as an operator
as an operator . Making use of Equation (10), we easily find [4]
. Making use of Equation (10), we easily find [4]
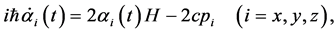 (11)
(11)
where 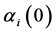 is the original matrix
is the original matrix ![]() of Equation (7) in schrödinger picture. Differentiation of both sides of Equation (11) by
of Equation (7) in schrödinger picture. Differentiation of both sides of Equation (11) by 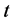 gives
gives
 (12)
(12)
The solution of the above differential equation is
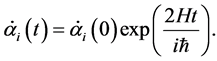 (13)
(13)
We substitute Equation (13) into Equation (11) to obtain
 (14)
(14)
Taking![]() , we have the above relation in another form.
, we have the above relation in another form.
 (15)
(15)
We finally obtain
 (16)
(16)
from Equations (15) and (14).
4. Solutions of Dirac Equation
For reader’s convenience, we summarize all equations in the following; they are necessary for our calculation. The Dirac equation
 (17)
(17)
has four eigen-solutions. We name these solutions 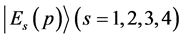 defined as
defined as
 (18)
(18)
where 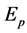 is the energy of a free Dirac electron with momentum
is the energy of a free Dirac electron with momentum![]() ,
,
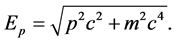 (19)
(19)
Two arrows  and
and 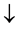 denote ‘Up Spin’ and ‘Down Spin’ respectively. The explicit forms of eigensolutions in Heisenberg picture are given by
denote ‘Up Spin’ and ‘Down Spin’ respectively. The explicit forms of eigensolutions in Heisenberg picture are given by
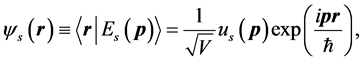 (20)
(20)
where ![]() is normalization volume, and
is normalization volume, and  are expressed as follows [16] ;
are expressed as follows [16] ;
 (21)
(21)
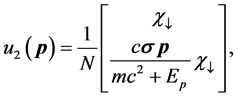 (22)
(22)
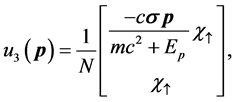 (23)
(23)
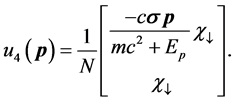 (24)
(24)
with normalization factor
 (25)
(25)
and eigen states of “Up Spin” and “Down Spin”,
 (26)
(26)
respectively. The momentum ![]() takes discrete values in normalization volume
takes discrete values in normalization volume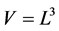 : That is
: That is 
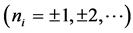 for
for . The functions
. The functions  are orthonormalized:
are orthonormalized:
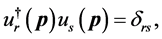 (27)
(27)
as well as
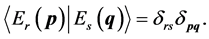 (28)
(28)
Next relations are especially important in a frame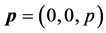 :
:
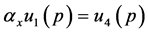 (29)
(29)
 (30)
(30)
Because each component of  satisfies
satisfies ,
, ![]() takes the eigenvalues
takes the eigenvalues  and
and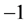 . This means the velocity
. This means the velocity 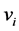 also has two eigenvalues
also has two eigenvalues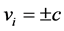 , that is the speed of light. However, states
, that is the speed of light. However, states  are not eigen states of
are not eigen states of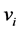 . An explicit form of
. An explicit form of 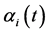 in the next section is applicable to the states
in the next section is applicable to the states .
.
5. Expectation Value of Zitterbewegung
In actual calculation, we will take z-axis along the momentum of the electron: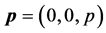 . This procedure is necessary in order to not only simplify our calculation but also exclude the z-component of angular momentum caused by orbital motion of the electron.
. This procedure is necessary in order to not only simplify our calculation but also exclude the z-component of angular momentum caused by orbital motion of the electron.
The velocity operator  is divided into two parts.
is divided into two parts.
 (31)
(31)
where
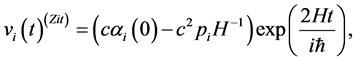 (32)
(32)
and
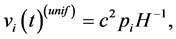 (33)
(33)
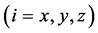 from Equation (16). The velocity
from Equation (16). The velocity 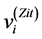 is Zitterbewegung part which includes oscillation factor, and
is Zitterbewegung part which includes oscillation factor, and  corresponds to uniform velocity. The coordinate operator
corresponds to uniform velocity. The coordinate operator 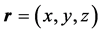 is also easily calculated from corresponding part of the above equations.
is also easily calculated from corresponding part of the above equations.
 (34)
(34)
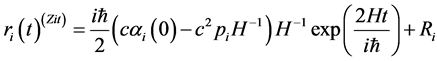 (35)
(35)
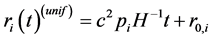 (36)
(36)
where ![]() is an integration constant, and
is an integration constant, and  agrees to an initial point of the electron in classical sense. Remembering that
agrees to an initial point of the electron in classical sense. Remembering that  is equal to the original
is equal to the original  of Equation (7), we easily calculate the expectation value of
of Equation (7), we easily calculate the expectation value of 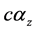 for
for  in our frame, by the use of relations in Sections 3 and 4.
in our frame, by the use of relations in Sections 3 and 4.
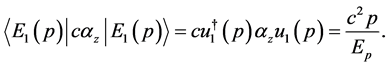 (37)
(37)
Equation (37) leads to
 (38)
(38)
 (39)
(39)
and
 (40)
(40)
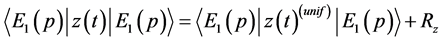 (41)
(41)
 (42)
(42)
where 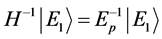 is used. Arbitrary constant
is used. Arbitrary constant 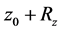 can set to zero without loss of generality. The similar results occur for x and y components of both
can set to zero without loss of generality. The similar results occur for x and y components of both  and
and . The contribution from uniform velocity vanish at this time because of
. The contribution from uniform velocity vanish at this time because of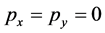 .
.
 (43)
(43)
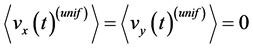 (44)
(44)
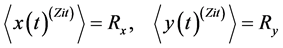 (45)
(45)
 (46)
(46)
where the expression of the expectation value for  is simplified. Results (38)-(46) indicate that Zitterbewegung (trembling motion) phenomenon for relativistic electron is un-observable effect in the sense that the expectation values of physical quantities always agree to classically measured one in accordance with Ehrenfest’s law [20] . A question whether Zitterbewegung works or not in actual physics phenomena then arises. The answer will be shown in the next section.
is simplified. Results (38)-(46) indicate that Zitterbewegung (trembling motion) phenomenon for relativistic electron is un-observable effect in the sense that the expectation values of physical quantities always agree to classically measured one in accordance with Ehrenfest’s law [20] . A question whether Zitterbewegung works or not in actual physics phenomena then arises. The answer will be shown in the next section.
6. Spin-Magnetic Moment
We calculate the magnetic moment based on Equation (4). As mentioned in Section 2, the velocity 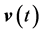 of relativistic electron is not equal to
of relativistic electron is not equal to  but equal to
but equal to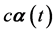 . So that the expression of magnetic moment
. So that the expression of magnetic moment ![]() must be
must be
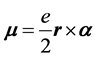 (47)
(47)
for relativistic electron. It is our advantage that we need no external magnetic field. In what follows, we pay attention to the electron in state , and to the z-component of the magnetic moment.
, and to the z-component of the magnetic moment.
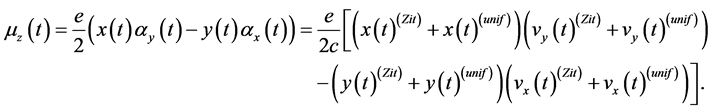 (48)
(48)
By the use of the completeness condition
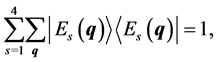 (49)
(49)
we have an expression of the expectation value of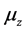 .
.
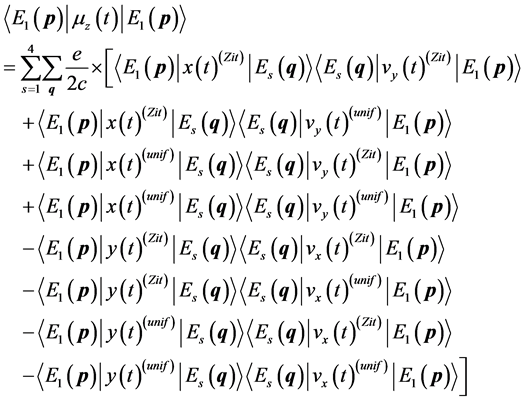 (50)
(50)
Each matrix elements of uniform part are calculated as follows:
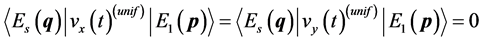 (51)
(51)
 (52)
(52)
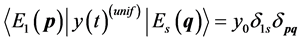 (53)
(53)
We have also Zitterbewegung part of the velocity.
 (54)
(54)
as well as
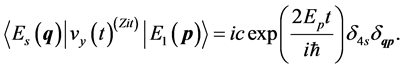 (55)
(55)
Substitution of Equations (51)-(55) into Equation (50) gives
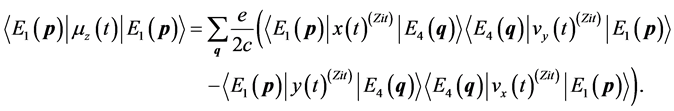 (56)
(56)
We find here that 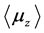 is made only by Zitterbewegung parts. We can easily obtain each element:
is made only by Zitterbewegung parts. We can easily obtain each element:
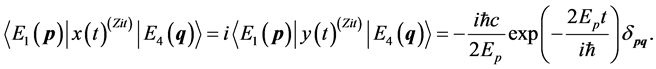 (57)
(57)
 (58)
(58)
We then finally obtain
 (59)
(59)
which is the same result as in the previous work [2] .
It is necessary to recall that there is not any z-component of magnetic moment arising from orbital motion of electron because of 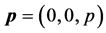 and
and 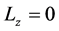 in our frame. Nevertheless, magnetic moment of Equation (59) has actually appeared. Therefore, we may conclude that
in our frame. Nevertheless, magnetic moment of Equation (59) has actually appeared. Therefore, we may conclude that  of Equation (59) and the spin-magnetic moment of the electron must be identified. When the momentum of the electron is small and
of Equation (59) and the spin-magnetic moment of the electron must be identified. When the momentum of the electron is small and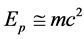 , it becomes
, it becomes
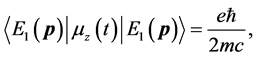 (60)
(60)
indicating correct ![]() -factor because of
-factor because of  for Dirac electron in our frame; that is
for Dirac electron in our frame; that is
 (61)
(61)
where ![]() is the
is the  spin matrix operator.
spin matrix operator.
7. Concluding Remarks
As seen in Sections 5, the expectation values of all Zitterbewegung parts give zero or constant, both in velocity and coordinates. This means that we can not directly measure the effect of Zitterbewegung. However, they still survive behind some kind of physical quantities. The magnetic moment is an example. Although Zitter-bewegung relating to the velocity or coordinates is un-observable in the sense of the expectation value which corresponds to classical behavior, we have shown that it exists and works through the magnetic moment. A crucial point is non-diagonal matrix elements: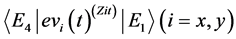 . The physical meaning of these matrix elements is inferred as follows:
. The physical meaning of these matrix elements is inferred as follows:
The initial state  of electron with positive energy and up-spin undergoes transition into the state
of electron with positive energy and up-spin undergoes transition into the state  with opposite signs of energy and spin (See Equations (29) and (30)), by operating
with opposite signs of energy and spin (See Equations (29) and (30)), by operating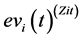 . This matrix element is a kind of “transition current” because it exactly corresponds to the electric current
. This matrix element is a kind of “transition current” because it exactly corresponds to the electric current ![]() in the definition of magnetic moment [2] which is written in another form [18] ,
in the definition of magnetic moment [2] which is written in another form [18] ,
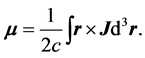 (62)
(62)
In quantum theory, the conservation law of energy may break by 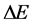 in time
in time![]() , where
, where
 (63)
(63)
The electron which has undergone transition into  must immediately return to
must immediately return to  within time
within time![]() . The period of transition cycle is about
. The period of transition cycle is about
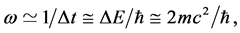 (64)
(64)
where  means the energy gap of Dirac Sea in vacuum. This
means the energy gap of Dirac Sea in vacuum. This 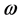 agrees with the frequency of Zitterbewegung (See Equations (57) and (58)).
agrees with the frequency of Zitterbewegung (See Equations (57) and (58)).
In the classical electrodynamics, the magnetic moment is caused by periodic orbital motion of a charged particles which is equivalent to an electric current. In the relativistic quantum theory, it seems that it is possible to cause the magnetic moment also by periodic transition from the positive energy state to the negative energy state (Figure 1). It then seems that the former is the magnetic moment which corresponds to Equation (5) with

Figure 1. Spin-magnetic moment caused by transition current.
 , and the latter is the spin-magnetic moment with
, and the latter is the spin-magnetic moment with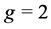 . In other word, the spin-magnetic moment may be caused not by usual electric current but by some new current which yield when the electron undergoes transition between two states of positive and negative energies. It should be noted that even an electron at rest (i.e.
. In other word, the spin-magnetic moment may be caused not by usual electric current but by some new current which yield when the electron undergoes transition between two states of positive and negative energies. It should be noted that even an electron at rest (i.e. 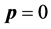 and
and![]() ) in space is able to yield this new current.
) in space is able to yield this new current.
8. Another Remarks
Such a situation as described above occurs in some kind of solid state. In the two band model of Cohen and Blount [21] , Wolff [22] indicated that the Hamiltonian takes the Dirac form after a suitable transformation, and that the resulting equations are essentially identical to those of the Dirac theory. This fact means that we could apply the method developed here to the spin-magnetic moment of electron in solid state [23] . Zawadzki [11] indeed pointed out that the energy of the electron in narrow-gap semiconductor was given as
 (65)
(65)
(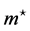 : effective mass), where
: effective mass), where  is maximum value of the group velocity
is maximum value of the group velocity ![]() of electron in band:
of electron in band:
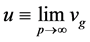 (66)
(66)
The Hamiltonian which corresponds to Equation (65) has the form
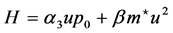 (67)
(67)
in the frame
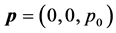
where 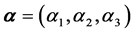 and
and 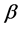 are the Dirac matrices. The above Hamiltonian agrees completely to the Dirac Hamiltonian in Equation (7) if we replace
are the Dirac matrices. The above Hamiltonian agrees completely to the Dirac Hamiltonian in Equation (7) if we replace  by
by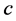 , and
, and  by
by . Obeying the Heisenberg equation of motion, it is then predicted that
. Obeying the Heisenberg equation of motion, it is then predicted that 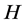 of the equal form reproduces the same results obtained here with the replacements
of the equal form reproduces the same results obtained here with the replacements 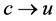 and
and . They will appear as a change of
. They will appear as a change of ![]() -factor of the electron in semiconductor from new equation corresponding to Equation (59).
-factor of the electron in semiconductor from new equation corresponding to Equation (59).
References
- Žutić, I., Fabian, J. and Sarma, S.D. (2004) Reviews of Modern Physics, 76, 323-410. http://dx.doi.org/10.1103/RevModPhys.76.323
- Sasabe, S. and Tsuchiya, K. (2008) Physics Letters A, 372, 381-386. http://dx.doi.org/10.1016/j.physleta.2007.07.078
- Schrödinger, E. (1930) Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl., 24, 418-428.
- Barut, A.O. and Bracken, A.J. (1981) Physical Review D, 23, 2454-2463. http://dx.doi.org/10.1103/PhysRevD.23.2454
- Sasabe, S. (2000) Electrical Engineering in Japan, 132, 1-6. http://dx.doi.org/10.1002/(SICI)1520-6416(20000715)132:1<1::AID-EEJ1>3.0.CO;2-O
- Castro, A.H., et al. (2009) Reviews of Modern Physics, 81, 109-162. http://dx.doi.org/10.1103/RevModPhys.81.109
- Zawadzki, W. and Rusin, T.M. (2011) Journal of Physics: Condensed Matter, 23, 143201. http://dx.doi.org/10.1088/0953-8984/23/14/143201
- Cannata, F., Ferrari, L. and Russo, G. (1990) Solid State Communications, 74, 309-312. http://dx.doi.org/10.1016/0038-1098(90)90192-E
- Ferrari, L. and Russo, G. (1990) Physical Review B, 42, 7454-7461. http://dx.doi.org/10.1103/PhysRevB.42.7454
- Rusin, T.M. and Zawadzki, W. (2007) Physical Review B, 76, 195439.
- Zawadzki, W. (2005) Physical Review B, 72, 085217. http://dx.doi.org/10.1103/PhysRevB.72.085217
- Katsnelson, M. (2006) The European Physical Journal B, 51, 157-160. http://dx.doi.org/10.1140/epjb/e2006-00203-1
- Zawadzki, W. (2006) Physical Review B, 74, 205439. http://dx.doi.org/10.1103/PhysRevB.74.205439
- Lurié, D. and Cremer, S. (1970) Physica, 50, 224-240. http://dx.doi.org/10.1016/0031-8914(70)90004-2
- Dirac, P.A.M. (1958) The Principle of Quantum Mechanics. Oxford University Press, Section 70.
- Schiff, L.I. (1968) Quantum Mechanics. McGraw-Hill, Section 43.
- Jackson, J.D. (1975) Classical Electrodynamics. John Wiley & Sons, New York, Section 5.6.
- Landau, L.D. and Lifschitz, E.M. (1975) The Classical Theory of Fields. Pergamon Press, Section 44.
- Dirac, P.A.M. (1958) The Principle of Quantum Mechanics. Oxford University Press, Section 67-69.
- Schiff, L.I. (1968) Quantum Mechanics. McGraw-Hill, Section 7.
- Cohen, M.H. and Blount, E.I. (1960) Philosophical Magazine, 5, 115-126. http://dx.doi.org/10.1080/14786436008243294
- Wolff, F.A. (1964) Journal of Physics and Chemistry of Solids, 25, 1057-1068. http://dx.doi.org/10.1016/0022-3697(64)90128-3
- Sasabe, S. and Tsuchiya, K. (2008) T. IEE Japan A, 128, 313-314.

